简介
现代金融市场是一个“自然”的复杂平衡体系的例子。一方面,市场相当混乱,因为它受到了大量参与者的影响。另一方面,市场具有一定的稳定过程,这是由市场参与者的行为决定的。经济物理学的任务之一是描述社会互动过程,形成在交易所观察到的价格动态。因此,定义和呈现金融时间序列的特定属性是非常可取的,这将使这些数据与其他自然过程区别开来。在现代理论中,价格序列被定义为不同规模的分形(从几分钟到几十年),
它们表现出比许多模型和自然过程更为复杂的行为[3]。找出这些行为细节的工具之一是对序列的数值分析,其目的是研究序列的动力学。分形维数可靠评估的典型算法需要大数据集(约10000-100000个样本),这些数据集描述了一个长时间间隔的序列,在此期间,行为可以改变,有时它可以反复改变。对于实际的交易任务,我们需要确定一系列局部分形特征的方法。在本文中,我们将讨论并演示一种使用[1,2]中描述的数值方法确定价格序列分形维数的方法。
分形维数的概念与时间序列的统计性质
分形维数估计数据集如何占用空间,分形维数的估计方法很多,它们的共同特征是体积或面积是在这个集合所在的空间中计算的。让我们使用金融工具的时间序列示例,它包括收盘价 {Close(t)},如果 {Close(t)} 系列级别是独立的,交易品种图表上没有明显的趋势,而行为将类似于“白噪声”。分形维数D的值将接近平面的拓扑维数的值,换句话说D->2。如果 {Close(t)} 序列水平不是独立的,D的值就会显著小于2,这表明时间序列具有一种“记忆”, 即在某些时间间隔内观察到向上和向下的趋势,与未定义的周期交替(图1)。
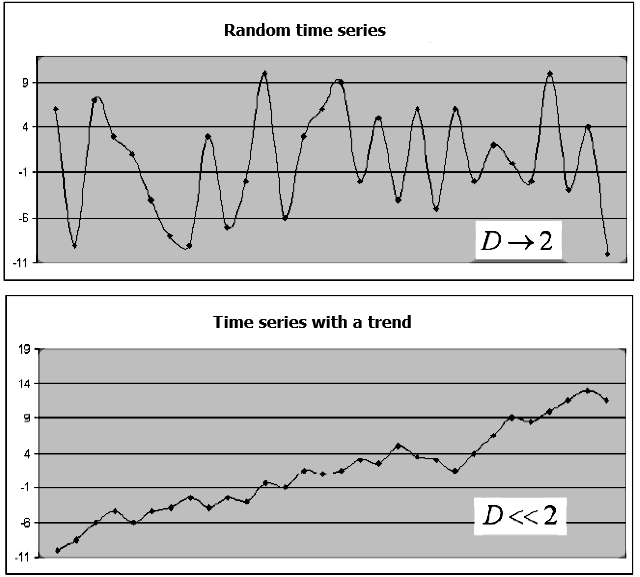
图1. 一个随机序列和一个趋势序列的例子,以及相应的分形维数
分形维数评价方法及其特征
计算时间序列的分形维数有不同的方法,让我们探讨使用 Hurst 指数的评估方法。
Hurst 指数 H 根据以下方程式确定
![]() (1a)
(1a)
其中尖括号表示时间平均。Hurst 指数与分形维数的关系是通过归一化范围法或基于以下方程的R/S分析得到的
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
其中 R — max {Close(t)} - min {Close(t)}, i = 1..N 是 Close(t) 序列偏移的范围, S — 是 Close(t) 值的标准差。这种方法在 Dmitry Piskarev 的 计算 Hurst 指数一文中有更加详细的描述。
如果时间序列的 Hurst 指数在0.5到1之间,则认为该序列是持久的,或是抗趋势的,这意味着 {Close(t)} 序列不是随机的,包含趋势,并且可以以足够的精度预测该序列的行为。H值越接近1,则 {Close(t)} 序列值之间的相关性越大。
这种方法的缺点是需要大量的数据(数千个数据序列值),以便获得Hurst指数的可靠估计,否则所获得的估计可能不正确。此外,序列值必须具有正态分布规律,这并不总是如此。由于对 DH 和 H 的可靠计算需要大量具有代表性的大数据量样本,因此序列行为在相关的长交易期内会反复变化。为了将分析过程的局部动力学与观察到的序列的分形维数相关联,我们需要局部确定D维度。
基于最小覆盖面积的分形维数估计
在预测经济计量序列时,一种更有效的方法是基于最小覆盖维度的计算[1,2]。1919年,Hausdorff 提出了以下确定分形的公式:
![]() .
.
其中
![]() 是半径最小的球数,
是半径最小的球数,
![]() 覆盖这一组。请注意,如果原始集合在欧几里得空间中,则任何其他简单形状(如单元格)都可以用于几何因子的集合近似
覆盖这一组。请注意,如果原始集合在欧几里得空间中,则任何其他简单形状(如单元格)都可以用于几何因子的集合近似
![]() ,而不是使用球覆盖集合。
,而不是使用球覆盖集合。
例如 f(t) 函数是在 [a, b] 之间设置的,让我们把区间切分开,l wm = [a=t0<t1<t2...tm=b], 其中切分的范围定义为
![]() 如果我们使用单元格大小
如果我们使用单元格大小
![]() 来覆盖这些集合,那么如果系数
来覆盖这些集合,那么如果系数
![]() 减少,则单元格的数目N将根据幂律增加:
减少,则单元格的数目N将根据幂律增加:
![]()
其中 D 是分形维度。
当使用单元格方法确定 D 维度时,将时间序列图所在的表面划分为大小小于的单元格,然后进行计算,以计算该图中至少一个点所属的单元格数 N()。然后改变,以双对数状态绘制 N()函数图。此外,使用最小二乘法(LS)对得到的点集进行近似。D 是基于线的斜率确定的。
在这个尺度上,函数图在 [a,b]区间的最小覆盖面积将等于以底和高等于变化-每个[ti-1,ti]区间的 f(t)函数的最大值和最小值之间的差的矩形面积之和。最小覆盖面积
![]() 可使用以下公式计算:
可使用以下公式计算:
![]() (2)
(2)
其中
![]() 是[a,b]区间内函数f(t)的振幅变化之和。估计值
是[a,b]区间内函数f(t)的振幅变化之和。估计值
![]() 取决于选定的震级。
取决于选定的震级。
![]() 越小,
越小,
![]() 的计算越精确。在这种情况下,当
的计算越精确。在这种情况下,当
![]() 发生变化时,值
发生变化时,值
![]() 根据功率排列而变化:
根据功率排列而变化:
![]() (3)
(3)
其中
![]() .
该值被称为“最小覆盖层的尺寸”,而索引被称为分形指数。
.
该值被称为“最小覆盖层的尺寸”,而索引被称为分形指数。
由32个观测值组成的时间序列的最小覆盖面积与不同
![]() 值的相关性如图2所示。
值的相关性如图2所示。
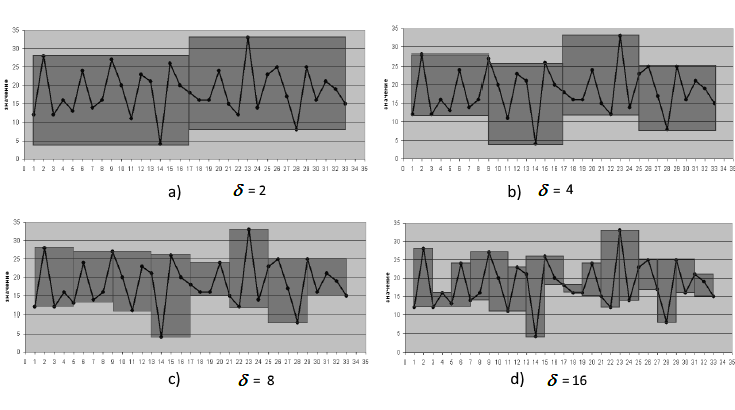
图 2. 用不同值计算覆盖面积
![]()
参考文献[2]指出,根据函数变化,使用单元格覆盖和矩形覆盖计算的分形维数是一致的。使用函数变化的算法的一个重要特性是其更快的收敛性,它允许使用一小组值在局部确定时间序列分形维数值。
将对数应用于(3),我们得到以下结果:
![]() (4)
(4)
为了确定
![]() ,使用最小二乘法(LS)在双对数坐标中绘制一个依赖(3)图,然后确定直线角的正切。根据表达式(4),计算
,使用最小二乘法(LS)在双对数坐标中绘制一个依赖(3)图,然后确定直线角的正切。根据表达式(4),计算
![]() 分形指数,这是时间序列的局部特征。如参考文献[1]所示,
分形指数,这是时间序列的局部特征。如参考文献[1]所示,
![]() 测定精度远高于其它分形特征的测定精度,如单元尺寸
测定精度远高于其它分形特征的测定精度,如单元尺寸
![]() 或基于Hurst指数计算的尺寸。此外,该方法对序列
或基于Hurst指数计算的尺寸。此外,该方法对序列
![]() 的分布没有限制。参考文献[1]还表明,如果时间序列
的分布没有限制。参考文献[1]还表明,如果时间序列
![]() 包含不少于32个观测值,则可获得可靠的估计值。通常,金融资产的历史要长得多。这种方法可以使用分形指数作为时间的函数,其中每个值都是根据时间序列的前32个值确定的。
包含不少于32个观测值,则可获得可靠的估计值。通常,金融资产的历史要长得多。这种方法可以使用分形指数作为时间的函数,其中每个值都是根据时间序列的前32个值确定的。
图3显示了根据近似直线的角度计算分形指数
![]() 的示例。根据该图,回归方程的确定系数R
2,这近似于依赖性,等于0.96-这表明分形指数0.4544是为一系列32点的片段计算的相当准确。
的示例。根据该图,回归方程的确定系数R
2,这近似于依赖性,等于0.96-这表明分形指数0.4544是为一系列32点的片段计算的相当准确。
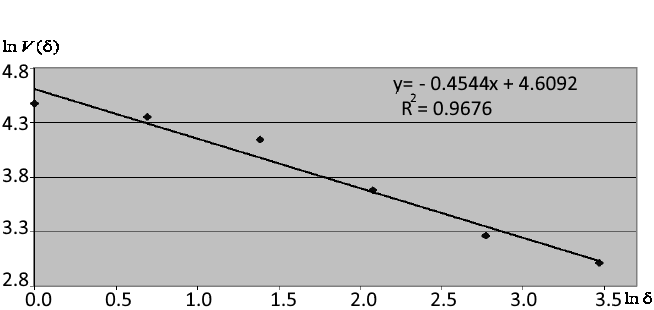
图3.双对数坐标中依赖性的近似值
![]() 和分形指数的确定
和分形指数的确定
分形维数的计算可以采用单元维数法或 Hurst 指数法。作为一个例子,让我们考虑卢克石油公司在本世纪初发生的危机之前的股票报价。这一时间可以解释为一个稳定的趋势,逐渐增加(持续的系列)。图4为1999年分形维数评价结果。
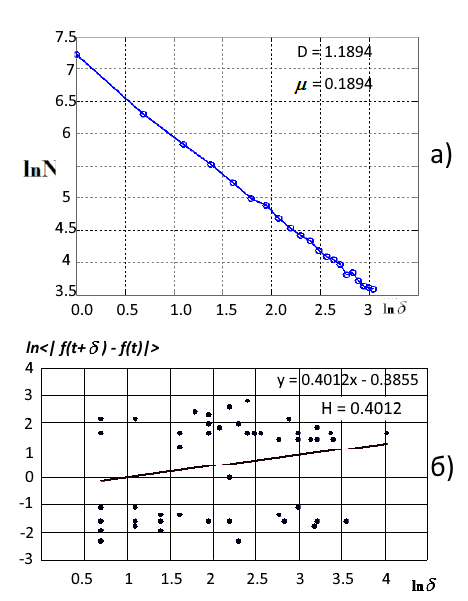
图 4. a) 使用单元覆盖(D=1.1894)的分形测量的 LS 近似,b)Hurst 参数数值估计的对数图(D=1.6)
该系列的分形维数D=1.18指向其持久的趋势性。接近1的值表示趋势接近尾声,发生在2000-2001年。Hurst 指数值 H=0.40. 注意相对较低的确定系数 R 2= 0.56 置信区间为 0.95. 根据公式(1),由Hurst指数计算的分形维数等于D=1.6,这表示A系列的随机行为和增加的随机性水平。然而,这与1999年卢克石油公司的股票无关。
参考文献[2]提供了另一个有趣且说明性的例子,说明了时间序列局部指标的分形指数和 Hurst
指数估计精度。该参数评估更适合于与市场分析相关的交易任务中操作性定性和定量的时间序列行为。美国铝业公司的源价格系列,包括8145点,分为8113个重叠区间,每个区间32天,相对移动一天。以下为计算精度参数:置信区间95%的宽度为
H 和
![]() ,实际点命中理论线的精度评估
K=1-R
2,其中R
2为确定系数(精确落线,然后R
2=1和K=0)。
,实际点命中理论线的精度评估
K=1-R
2,其中R
2为确定系数(精确落线,然后R
2=1和K=0)。
在8113个间隔中计算出以下值:
- H — Hurst exponent;
-
 —
分形指数;
—
分形指数; -
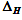 — H的置信区间宽度95%
— H的置信区间宽度95% -
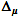 —
—
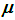 置信区间的95%宽度
置信区间的95%宽度 -
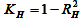 - H的实验和获得的直线对应的准确度;
- H的实验和获得的直线对应的准确度; -
 -
实验结果与得到的直线符合度
-
实验结果与得到的直线符合度
 。
。
函数图形的典型片段
![]() ,
,
![]() 以及
以及
![]() ,
,
![]() ,
为间隔建立,正确的值与时间一致 t, 在图 5a 和 5b 中显示. 从这些数据可以看出,在大多数情况下,指数
,
为间隔建立,正确的值与时间一致 t, 在图 5a 和 5b 中显示. 从这些数据可以看出,在大多数情况下,指数
![]() 比
H的判断更加准确。
比
H的判断更加准确。
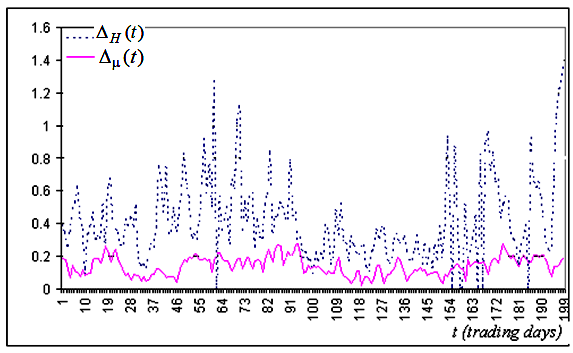
图 5a. 基于收盘价序列创建的置信区间宽度时间序列的典型片段 Alcoa Inc.
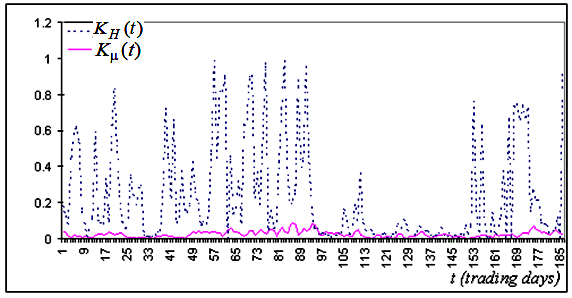
图 5b. 实验点与理论线重合精度值对应的序列片段, 使用相同序列
基于这些图像,我们可以得出结论,在绝大多数情况下,分形指数
![]() 的确定比H
更加精确.
的确定比H
更加精确.
与其他分形指标(尤其是 Hurst 指数)相比,指数
![]() 的主要优点是相应的
的主要优点是相应的
![]() 值快速进入渐近模式。这使得可以通过确定初始过程的动力学来使用
值快速进入渐近模式。这使得可以通过确定初始过程的动力学来使用
![]() 作为局部特征,因为其精确测定的刻度顺序与确定过程状态的主刻度的顺序相匹配。这些状态包括相对平静期(平)和长期向上或向下运动期(趋势)。将值
作为局部特征,因为其精确测定的刻度顺序与确定过程状态的主刻度的顺序相匹配。这些状态包括相对平静期(平)和长期向上或向下运动期(趋势)。将值
![]() 与序列行为相关联的有效解决方案是将函数
与序列行为相关联的有效解决方案是将函数
![]() 添加为值
添加为值
![]() ,在 t之前的最小间隔中确定,其中
,在 t之前的最小间隔中确定,其中
![]() 仍然可以以可接受的精度计算。
仍然可以以可接受的精度计算。
时间序列性质与分形指数的相关性
任何愿意使用基于分形指数的指标的人都应该知道它的一些特定特征[2]。
系列的行为定义了
![]() 值:
值:
-
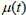 =
0.5 表示随机价格波动(维纳过程)投资者行为独立,价格走势不明显。在这种情况下,我们可以说价格具有“正常”的稳定性,因为价格对外部影响的依赖性较弱,没有“反馈”,因此没有套利机会。
=
0.5 表示随机价格波动(维纳过程)投资者行为独立,价格走势不明显。在这种情况下,我们可以说价格具有“正常”的稳定性,因为价格对外部影响的依赖性较弱,没有“反馈”,因此没有套利机会。 -
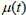 <
0.5
表明该价格对外部影响具有较高的稳定性,这与投资者对相关公司稳定性的信心以及市场上没有任何新信息有关。在这种情况下,股票价格在相当窄的价格范围内波动。当价格上涨时仍有足够的卖家,当价格下跌时也有足够的买家,他们的行为使价格回到初始范围。在这种情况下,“相关性”是负的,它在保持稳定的价格行为的同时减轻了股票价格的变化。
<
0.5
表明该价格对外部影响具有较高的稳定性,这与投资者对相关公司稳定性的信心以及市场上没有任何新信息有关。在这种情况下,股票价格在相当窄的价格范围内波动。当价格上涨时仍有足够的卖家,当价格下跌时也有足够的买家,他们的行为使价格回到初始范围。在这种情况下,“相关性”是负的,它在保持稳定的价格行为的同时减轻了股票价格的变化。 -
 >
0.5
对应于降低的价格稳定性。这可能表明新信息的出现和对此信息的反应。可以假设,所有市场参与者对输入信息的估计大致相等,因此,与所收到的信息相对应的价格变动出现了趋势。某些情况下,这种情况会导致股票价格的急剧变化。
>
0.5
对应于降低的价格稳定性。这可能表明新信息的出现和对此信息的反应。可以假设,所有市场参与者对输入信息的估计大致相等,因此,与所收到的信息相对应的价格变动出现了趋势。某些情况下,这种情况会导致股票价格的急剧变化。
分形指数和赫斯特指数相关为
![]() =1-H, 这使得从混沌时间序列中继承分类变量:
=1-H, 这使得从混沌时间序列中继承分类变量:
- 当
 =
0.5, H = 0.5 时间序列是维纳过程(“布朗”噪声)。这个过程的主要特性是没有内存:序列演化与以前的值没有联系。
=
0.5, H = 0.5 时间序列是维纳过程(“布朗”噪声)。这个过程的主要特性是没有内存:序列演化与以前的值没有联系。 - 当 0.5 <
 <= 1,
0 <= H < 0.5, 这个过程被认为是“粉红色”的噪音。它的特点是“负”记忆:如果过去记录的是正增量,它可能后面跟着负增量,反之亦然。
<= 1,
0 <= H < 0.5, 这个过程被认为是“粉红色”的噪音。它的特点是“负”记忆:如果过去记录的是正增量,它可能后面跟着负增量,反之亦然。 - 如果 0 <=
 <
0.5 , 0.5 < H <=1, 时间序列是一种带有积极记忆的“黑色”噪声:如果过去发生了积极的趋势,它很可能会在未来继续存在,反之亦然。
<
0.5 , 0.5 < H <=1, 时间序列是一种带有积极记忆的“黑色”噪声:如果过去发生了积极的趋势,它很可能会在未来继续存在,反之亦然。
分形指数和 Hurst 指数的评价指标
以天、周和月为尺度的成功交易与对金融时间序列混乱状态的理解有关。在对短数据片段中的分形指标进行稳定评估的基础上,我们可以开发出一种股票指标(其演化是由大量人的意志决定的),这将有助于交易者识别和预测金融时间序列。
该指标评估了分形指数、分形指数的置信区间、确定系数的值和 Hurst 指数。下面的图表显示了上述
![]() ,
,
![]() ,
和
,
和
![]() 函数图。
函数图。
在指标中,可以设置时间序列段的长度,对其进行计算,并提供参数评估窗口。指标发布时,该系列按收盘价计算,而窗口移动一个计数。由于评价窗口(区间)的长度等于二的幂次,我们可以通过对其进行线性逼近得到一组数值,并对其分形指数进行评价。
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - time series // N0, N1 - the left and right boundary points of the series[] array fragment, based on which the fractal index will be estimated // hourSampling - discretization between points in HOURS // CountFragmentScale - the number of requested scales to form a set of points, for which the fractal index is calculated // // RESULT // the fractal index (Mu), the Hurst index (Hurst), the Confidence interval 95% (ConfInterval[2], // coefficient of determination (R2det) - the closer to 1, the more accurately the calculation points fall on the approximating line // determining stability for coefficient KR2 = 1-R2det. The closer to zero, the more accurate the calculated value of Mu //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Load the internal fragment with values from the time series LoadFragment(series,N0,N1,hourSampling); // 2. Determine the number of cycles to determine the points of the approximating line int nn2 = (int)floor(Nfrgm/2); // Partition limits - no less than two points int npow2 = (int)ipow2(nn2); // The number of the powers of two in the Possible partitioning limit; if(CountFragmentScale==0) CountFragmentScale=npow2; // default int Count=fmin(CountFragmentScale,npow2); // limiting the number of variants of series fragment division int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Number of pieces in the series fragment division CalcAmplVariation(NumPartDivide, i); // Calculating a point for the approximating line model i=i; } // 4. Evaluation of the Fractal Index and on the limits of the Index confidence intervals Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Hurst exponent KR2=1-R2det; return Mu; } //----------------------------------------------------------------------------------------------------------------------------------
double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // If idxAmplVar=-1, then index in the array is determined automatically (based on the contribution of the power of two in NumPartDivide) // ALREADY PREVIOUSLY DONE: copying the fragment, setting the time of discretization of the series IN DAYS // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. DETERMINE THE BORDERS OF INTERVALS CORRESPONDING TO THE SPECIFIC NUMBERS int nCheckPoint=0,nIntervalPoints=0; // the number of points to check in one division interval double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. GO THROUGH INTERVALS TO DETERMINE LIMIT VALUES OF FUNCTIONS AND OF AMPLITUDE VARIATION int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // INDEX WITH MAX. VALUE minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. ACCUMULATION OF RESULTS IN STORAGE if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // index in the storage array LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // log-scale of the current division LogAmplVariations[idxAmplVar] = log(V); // log-Amplitude Variation in the current division scale return V; } //--------------------------------------------------------------------------------------------------------------------------------------
CFragmentIndexLine.mqh 文件片段执行覆盖面积计算循环,如图2所示。程序中的操作顺序通过详细的注释进行解释。
实际数据指标操作演示
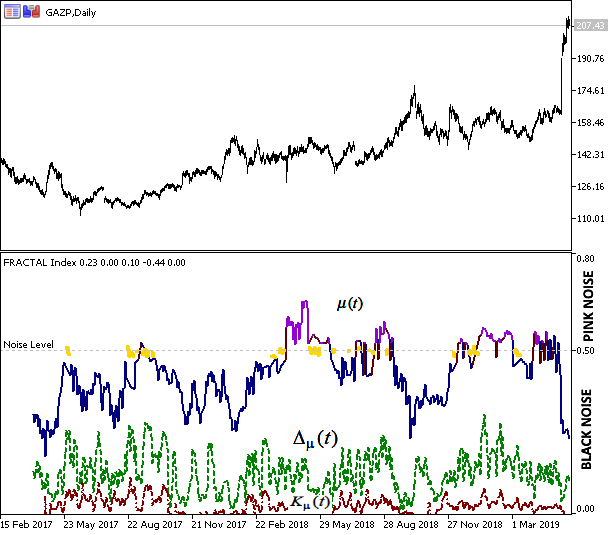
图6 俄罗斯天然气工业股份公司收盘价及分形指数评价结果
该图显示了指数值与价格行为的相关性,指数图的蓝色对应于系统的趋势状态,表明趋势的稳定性和预测未来行为的能力。紫罗兰色表示“粉色噪音”类型的抗持久性,对应于“负”记忆和平坦。黄色对应“布朗运动”,即运动是随机的,无法预测。
结论
本地分形分析在交易中可能很有趣,其目的如下:
- 确定无序状态,即时间序列的统计特征发生变化的时刻;
- 时间序列的预测。
应考虑到,在计算Hurst 指数 H 时,以适当精度确定指数
![]() 的比例比类似比例小两个数量级。这种差异允许使用指数
的比例比类似比例小两个数量级。这种差异允许使用指数
![]() 作为局部分形指数。这就是为什么可以认为指数
作为局部分形指数。这就是为什么可以认为指数
![]() 描述了时间序列的稳定性。假如
描述了时间序列的稳定性。假如
![]() <0.5可以解释为趋势,假如
<0.5可以解释为趋势,假如
![]() >0.5可以被视为平盘。
>0.5可以被视为平盘。
![]() ~
0.5 当成布朗运动。因此,使用函数
~
0.5 当成布朗运动。因此,使用函数
![]() 我们可以对初始价格系列进行分类,并为预测提供基础。
我们可以对初始价格系列进行分类,并为预测提供基础。
参考文献列表
- Dubovikov M.M., Starchenko N.V. 金融资产时间序列的经济学与分形分析
- Dubovikov M.M., Starchenko N.V. 经济学与金融时间序列分析"经济物理学. 现代物理学寻求经济理论”
- Peters, J. 资本市场的混乱与秩序:周期、价格和市场波动的新视角
- Krivonosova
E.K., Pervadchuk V.P., Krivonosova E.A.经济指标时间序列的分形特征比较
- Starchenko N.V. 物理应用中的局部分形分析。









