内容
- 概述
- 1. 常规化的理论前提
- 2. 实现
- 2.1. 为我们的模型创建新的类
- 2.2. 前馈
- 2.3. 反馈
- 2.4. 神经网络基类的变化
- 3. 测试
- 结束语
- 参考
- 本文中用到的程序
概述
在上一篇文章中,我们开始研究旨在提升神经网络收敛性的方法,并体验了其中一种减少特征协适应的舍弃(Dropout)方法。 我们来继续这个话题,并掌握常规化方法。
1. 常规化的理论前提
在神经网络应用实践中运用了多种数据常规化方法。 然而,它们的作用均是为了令训练样本数据和神经网络隐藏层的输出保持在一定范围内,并具有某些样本统计特征,如方差和中位数。 这一点很重要,因为网络神经元在训练过程中利用线性变换将样本朝逆梯度偏移。
参考一个含有两个隐藏层的全连接感知器。 在前馈验算过程中,每一层都会生成一个特定的数据集,作为下一层的训练样本。 输出层的结果与参考数据进行比较。 然后,在反馈验算过程中,误差梯度自输出层穿过隐藏层朝向初始数据传播。 每个神经元接收到误差梯度后,我们更新权重系数,为最后一次前馈验算的训练样本调整神经网络。 此处会产生一个冲突:第二个隐藏层(下图中的 H2)会基于第一个隐藏层(图中的 H1)输出的数据样本进行调整,而通过改变第一个隐藏层的参数,我们已更改了数据数组。 换言之,我们调整第二个隐藏层,其数据样本不再存在。 类似的状况也发生在输出层,因第二个隐藏层输出业已变化,故它也会被调整。 如果我们参考第一和第二隐藏层之间的失真,误差尺度会更大。 神经网络越深,影响越强。 这种现象被称为内部协变量偏移。
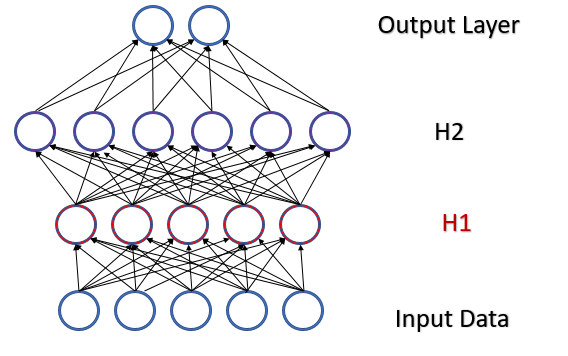
经典神经网络通过降低学习率部分解决了这个问题。 权重的微小变化不会导致神经层输出的样本分布发生显著变化。 但这种方式并未解决随着神经网络层数增加而出现的问题放大,且还降低了学习速度。 减小学习率的另一个问题是该过程可能会卡在局部最小值上,我们曾在第六篇文章里讨论过。
2015 年 2 月,Sergey Ioffe 和 Christian Szegedy 提出了批次常规化作为内部协方差偏移问题的解决方案 [13]。 该方法的思路是在特定时间间隔内把每个单独的神经元进行常规化,样本(批次)的中位数向零偏移,并令样本方差为 1。
常规化算法如下。 首先,计算数据批次的平均值。
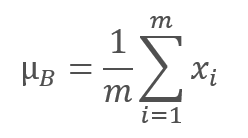
此处的 m 是批次大小。
然后计算原始批次的方差。
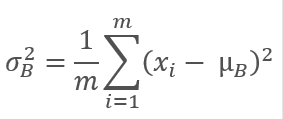
对批次数据进行常规化,令批次均值为零,且方差为 1。
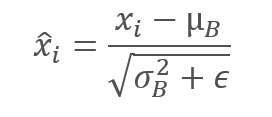
请注意,为避免除零,在批次方差的分母中增加了一个常数 ϵ,一个小正数。
然而,事实证明,这种常规化会令原始数据的影响失真。 因此,该方法的作者又增加了一个步骤:缩放和偏移。 他们引入了两个变量,γ 和 β,采用梯度下降法在神经网络里一并训练。
![]()
应用该方法可令训练的每一步获得的数据批次均拥有相同分布,如此令神经网络训练更加稳定,且可以提高学习率。 一般来说,这种方法有助于提高训练品质,同时减少神经网络训练所花费的时间。
然而,这会增加存储额外学习率的成本。 还有,需要存储整个批次大小的每个神经元的历史数据,以便计算平均值和离散度。 在此,我们能够检查指数平均的应用。 下图展示了 100 个元素的移动平均和移动方差,与相同的 100 个元素的指数移动平均和指数移动方差的对比图。 该图表是依据介于 -1.0 和 1.0 之间的 1000 个随机元素构建的。
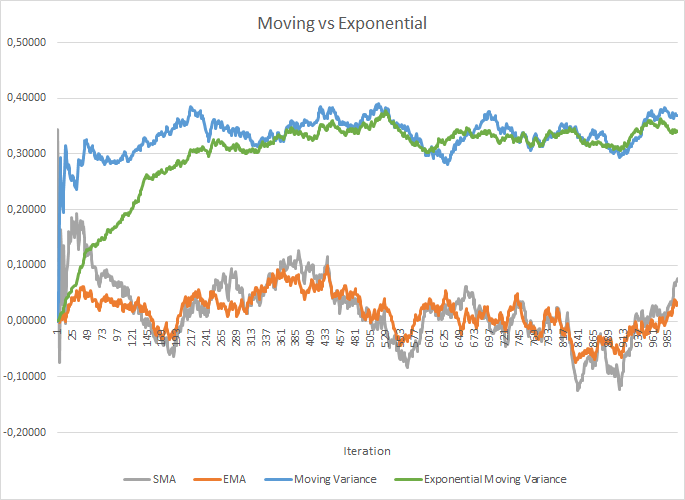
在这个图表中,移动平均线和指数移动平均线经过 120-130 次迭代后彼此接近,然后偏差最小(因此可被忽略)。 此外,指数移动平均图更平滑。 EMA 可依据已知的函数前值和序列的当前元素来计算。 我们来看看指数移动平均线的公式。
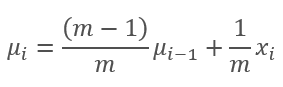 ,
,
其中
- m 是批次大小,
- i 是迭代索引。
它用更多的迭代 (310-320) 才能令移动方差和指数移动方差图更接近,但总体概貌类似。 在方差的情况下,采用指数算法不仅可以节省内存,还可以显著减少计算次数,因为移动方差是依据整个批次计算来自均值的偏差。
该方法作者进行的实验表明,采用批次常规化方法还可用作规范器。 这能减少了对其他规范方法的需求,包括之前研究的舍弃。 进而,后续的研究表明,舍弃和批次常规化的组合运用,会对神经网络学习结果有负面影响。
所提议的常规化算法可在现代神经网络架构的各种变体中找到。 作者建议在非线性(激活公式)之前使用批次常规化 可参考 2016 年 7 月提出的层常规化方法作为该算法的变体之一。 我们在研究关注机制(第九篇文章)的时候曾研讨过该方法。
2. 实现
2.1 为我们的模型创建新的类
我们已经研究过理论方面,现在我们在函数库中实现它。 我们创建一个新类 CNeuronBatchNormOCL 来实现该算法。
class CNeuronBatchNormOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; ///< Pointer to the object of the previous layer uint iBatchSize; ///< Batch size CBufferDouble *BatchOptions; ///< Container of method parameters ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::BatchFeedForward().@param NeuronOCL Pointer to previous layer. ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateBatchOptionsMomentum() or ::UpdateBatchOptionsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previous layer. public: /** Constructor */CNeuronBatchNormOCL(void); /** Destructor */~CNeuronBatchNormOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, uint batchSize, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (iBatchSize>1 ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (iBatchSize>1 ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (iBatchSize>1 ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (iBatchSize>1 ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (iBatchSize>1 ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradientBatch(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronBatchNormOCL; }///< Identificator of class.@return Type of class };
新类将自 CNeuronBaseOCL 基类继承。 如同 CNeuronDropoutOCL 类一样外推,我们添加 PrevLayer 变量。 当指定的批次尺寸小于 “2” 时,将应用上一篇文章中展示的数据缓冲区替换方法,将其保存到 iBatchSize 变量之中。
批次常规化算法需要保存一些参数,这些参数对于已常规化层的每个神经元都是独立的。 出于避免为每个单独的参数生成过多的单独缓冲区,我们将为这些参数创建含有以下结构的单一 BatchOptions 缓冲区。

从呈现的结构可以看出,参数缓冲区的大小将取决于所采用的参数优化方法,因此其会在类初始化方法中创建。
类方法的集合都已经标准化。 我们来查看它们。 在类构造函数中,我们重置指向对象的指针,并将批次尺寸设置为 1,其实质是把层从网络操作中排除,直至它被初始化。
CNeuronBatchNormOCL::CNeuronBatchNormOCL(void) : iBatchSize(1) { PrevLayer=NULL; BatchOptions=NULL; }
在类的析构函数中,删除参数缓冲区对象,并将指向上一层的指针清零。 请注意,我们不会删除前一层的对象,而只是将指针清零。 该对象将在创建它的所在被删除。
CNeuronBatchNormOCL::~CNeuronBatchNormOCL(void) { if(CheckPointer(PrevLayer)!=POINTER_INVALID) PrevLayer=NULL; if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; }
现在,来研究类初始化方法 CNeuronBatchNormOCL::Init。 所需传递的类参数:下一层的神经元数量、识别神经元的索引、指向 OpenCL 对象的指针、在常规化层中的神经元数量、批次尺寸和参数优化方法。
在方法的伊始,调用父类的相关方法,在其内初始化基本变量和数据缓冲区。 然后保存批次尺寸,并为层激活函数设置为 None。
请注意激活函数。 运用该函数需取决于神经网络架构。 如果神经网络架构需要在激活函数之前嵌入常规化,如同该方法的作者所建议的那样,必须在前一层禁用激活函数,且必须在常规化层中指定所需的函数。 从技术上讲,激活函数是在初始化类实例之后,调用父类的 SetActivationFunction 方法来指定的。 取决于网络架构,若需要在激活函数之后使用常规化,那么激活方法应该在前一层里指定,且在常规化所在层没有激活函数。
bool CNeuronBatchNormOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons,uint batchSize,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,numNeurons,optimization_type)) return false; activation=None; iBatchSize=batchSize; //--- if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; int count=(int)numNeurons*(optimization_type==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferInit(count,0)) return false; //--- return true; }
在方法的末尾,我们创建了一个参数缓冲区。 如上所述,缓冲区尺寸取决于层中的神经元数量和参数优化方法。 当使用 SGD 时,我们为每个神经元保留 7 个元素;当使用 Adam 方法优化时,每个神经元需要 9 个缓冲元素。 成功创建所有缓冲区之后,该方法以 true 退出。
附件中提供了所有类及其方法的完整代码。
2.2. 前馈
在下一步里,我们来研究前馈验算。 我们首研究虑直接验算 BatchFeedForward。 每个单独的神经元均会启动内核算法。
内核在参数中接收指向 3 个缓冲区的指针:初始数据、参数缓冲区、和写入结果的缓冲区。 此外,在参数里传递批次尺寸、优化方法和神经元激活算法。
在内核伊始,检查指定的常规化窗口尺寸。 如果针对一个神经元进行常规化,则退出该方法而不进一步执行操作。
验证成功之后,我们得到数据流标识符,其指示在输入数据张量中常规化数值的位置。 基于标识符,我们可以判断在常规化参数张量中第一个参数的偏移。 在这一步,优化方法将建议参数缓冲区的结构。
接着,计算这一步的指数均值和方差。 基于这些数据,计算我们元素的常规化数值。
批次常规化算法的下一步是偏移和缩放。 早前,在初始化期间,我们以零值来填充参数缓冲区,故如果我们在第一步“以其纯粹形式”执行此操作,我们将得到 “0”。 为避免于此,需检查 γ 参数的当前值,如果它等于 “0”,则将其值更改为 “1”。 保留偏移值为零。 以这种形式执行偏移和缩放。
__kernel void BatchFeedForward(__global double *inputs, __global double *options, __global double *output, int batch int optimization, int activation) { if(batch<=1) return; int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- for(int i=0;i<(optimization==0 ? 7 : 9);i++) if(isnan(options[shift+i])) options[shift+i]=0; //--- double mean=(options[shift]*((double)batch-1)+inputs[n])/((double)batch); double delt=inputs[n]-mean; double variance=options[shift+1]*((double)batch-1.0)+pow(delt,2); if(options[shift+1]>0) variance/=(double)batch; double nx=delt/sqrt(variance+1e-6); //--- if(options[shift+3]==0) options[shift+3]=1; //--- double res=options[shift+3]*nx+options[shift+4]; switch(activation) { case 0: res=tanh(clamp(res,-20.0,20.0)); break; case 1: res=1/(1+exp(-clamp(res,-20.0,20.0))); break; case 2: if(res<0) res*=0.01; break; default: break; } //--- options[shift]=mean; options[shift+1]=variance; options[shift+2]=nx; output[n]=res; }
获得常规化数值之后,我们检查是否需要在该层上执行激活函数,并执行必要动作。
现在,简单地把新值保存到数据缓冲区,并退出内核。
BatchFeedForward 内核构建算法相当简单,故我们可以继续创建从主程序调用内核的方法。 此功能将由 CNeuronBatchNormOCL::feedForward 方法实现。该方法的算法与其他类的相关方法类似。 该方法在参数中接收一个指向神经网络前一层的指针。
在该方法的开头,检查收到的指针和指向 OpenCL 对象指针的有效性(您可能还记得这是操控 OpenCL 程序的标准库类的副本)。
在下一步里,保存指向神经网络上一层的指针,并检查批次尺寸。 如果常规化窗口的大小不超过 “1”,则复制上一层激活函数的类型,并以 true 结果退出方法。 以这种方式,我们提供了替换缓冲区的数据,并排剔除了不必要的算法迭代。
bool CNeuronBatchNormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- PrevLayer=NeuronOCL; if(iBatchSize<=1) { activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); return true; } //--- if(CheckPointer(BatchOptions)==POINTER_INVALID) { int count=Neurons()*(optimization==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(!BatchOptions.BufferInit(count,0)) return false; } if(!BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_inputs,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_output,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_optimization,(int)optimization)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_activation,(int)activation)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_BatchFeedForward,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch Feed Forward: %d",GetLastError()); return false; } if(!Output.BufferRead() || !BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
如果在所有检查之后,我们已到达直接验算内核的启动,我们还需要为启动它准备初始数据。 首先,检查常规化算法的参数缓冲区指针的有效性。 若有必要,创建并初始化一个新的缓冲区。 接着,在显卡内存中创建一个缓冲区,并加载缓冲区内容。
设置需启动线程的数量,其值等于层中神经元的数量,并将指向数据缓冲区的指针,以及所需参数传递至内核。
所有准备工作完成之后,发送内核执行,并从显卡内存中读回更新后的缓冲区数据。 请注意,从显卡接收的数据来自两个缓冲区:来自算法输出的信息,和参数缓冲区,在其中我们保存了更新后的均值、方差和常规化数值。 该数据将用于进一步的迭代。
算法完成后,从显卡内存中删除参数缓冲区,从而释放神经网络深层缓冲区的内存。 然后,以 true 退出该方法。
附件中提供了函数库中所有类及其方法的完整代码。
2.3. 反馈
反馈验算还是由两个阶段组成:误差反向传播和权重更新。 替代通常的权重,我们将训练缩放和偏移函数的参数 γ 和 β。
我们从梯度下降函数开始。 创建内核 CalcHiddenGradientBatch 来实现功能。 内核从参数里接收一些指针:来自下一层梯度的常规化参数张量、前一层输出数据(在最后一次前馈验算期间获得的)、和前一层梯度张量的指针(算法结果将写入这个张量)。 内核还在参数里接收:批次尺寸、激活函数的类型、和参数优化方法。
与直接验算一样,在内核开始时检查批次尺寸,如果小于或等于 1,则不执行其他迭代退出内核。
下一步是获取线程的序列号,并判断参数张量的偏移。 这些动作类似于之前在前馈验算中讲述的动作。
__kernel void CalcHiddenGradientBatch(__global double *options, ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer __global double *matrix_i, ///<[in] Tensor of previous layer output __global double *matrix_ig, ///<[out] Tensor of gradients at previous layer uint activation, ///< Activation type (#ENUM_ACTIVATION) int batch, ///< Batch size int optimization ///< Optimization type ) { if(batch<=1) return; //--- int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- double inp=matrix_i[n]; double gnx=matrix_g[n]*options[shift+3]; double temp=1/sqrt(options[shift+1]+1e-6); double gmu=(-temp)*gnx; double gvar=(options[shift]*inp)/(2*pow(options[shift+1]+1.0e-6,3/2))*gnx; double gx=temp*gnx+gmu/batch+gvar*2*inp/batch*pow((double)(batch-1)/batch,2.0); //--- if(isnan(gx)) gx=0; switch(activation) { case 0: gx=clamp(gx+inp,-1.0,1.0)-inp; gx=gx*(1-pow(inp==1 || inp==-1 ? 0.99999999 : inp,2)); break; case 1: gx=clamp(gx+inp,0.0,1.0)-inp; gx=gx*(inp==0 || inp==1 ? 0.00000001 : (inp*(1-inp))); break; case 2: if(inp<0) gx*=0.01; break; default: break; } matrix_ig[n]=clamp(gx,-MAX_GRADIENT,MAX_GRADIENT); }
接下来,顺序计算所有函数的梯度。

最后,穿过前一层的激活函数传播梯度。 将结果值保存在前一层的梯度张量。
继 CalcHiddenGradientBatсh 内核之后,我们来研究 CNeuronBatchNormOCL::calcInputGradients 方法,该方法将从主程序启动内核执行。 与其他类的相关方法相似,该方法在参数中接收一个指向前一神经网络层对象的指针。
在方法的开头,检查收到的指针和指向 OpenCL 对象指针的有效性。 之后,检查批次大小。 如果小于或等于 1,则退出该方法。 从该方法返回的结果取决于指向前一层指针的有效性,该指针是在前馈验算期间保存的。
如果我们继续深入算法,检查参数缓冲区的有效性。 如果发生错误,则以 false 退出该方法。
请注意,所传播梯度属于最后一次前馈验算。 这就是为什么在最后两个控制点,我们需检查参与前馈的对象。
bool CNeuronBatchNormOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_ig,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_activation,NeuronOCL.Activation())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_optimization,(int)optimization)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_CalcHiddenGradientBatch,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch CalcHiddenGradient: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
与前馈验算一样,启动的内核线程数量将等于该层中神经元的数量。 将常规化参数缓冲区的内容发送到显卡内存,并将所需的张量和参数指针传递给内核。
上述所有操作执行完毕之后,运行内核执行,并计算来自显卡内存的结果梯度,保存至相应缓冲区。
在该方法末尾,从显卡内存中删除常规化参数的张量,并以结果 true 退出该方法。
传播梯度后,是时候更新偏移和缩放参数了。 为了实现这些迭代,根据前面所讲述的优化方法数量,创建 2 个内核 UpdateBatchOptionsMomentum 和 UpdateBatchOptionsAdam。
我们先从 UpdateBatchOptionsMomentum 方法开始。 该方法从参数里接收指向两个张量的指针:常规化参数,和/或,梯度。 此外,在方法参数中传递优化方法常量:学习率和动量。
在内核伊始,获取线程数量,并判定常规化参数张量的偏移。
依据源数据,我们计算 γ 和 β 的增量。 为该操作,我采用了含有 2 个元素的双精度型向量进行计算。 这种方法允许并行计算。
调整参数 γ、β,并将结果保存在常规化参数张量的相应元素之中。
__kernel void UpdateBatchOptionsMomentum(__global double *options, ///<[in,out] Options matrix m*7, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer double learning_rates, ///< Learning rates double momentum ///< Momentum multiplier ) { const int n=get_global_id(0); const int shift=n*7; double grad=matrix_g[n]; //--- double2 delta=learning_rates*grad*(double2)(options[shift+2],1) + momentum*(double2)(options[shift+5],options[shift+6]); if(!isnan(delta.s0) && !isnan(delta.s1)) { options[shift+5]=delta.s0; options[shift+3]=clamp(options[shift+3]+delta.s0,-MAX_WEIGHT,MAX_WEIGHT); options[shift+6]=delta.s1; options[shift+4]=clamp(options[shift+4]+delta.s1,-MAX_WEIGHT,MAX_WEIGHT); } };
UpdateBatchOptionsAdam 内核是按照类似的方案构建的,但在优化方法的算法上有所差异。 内核从参数里接收指向相同参数和梯度张量的指针。 它还接收优化方法参数。
在内核伊始,定义线程数量,并判定参数张量的偏移。
基于获得的数据,计算第一和第二动量。 此处所用的矢量计算,能够同时计算两个参数的动量。
基于获得的动量,计算增量和新参数值。 计算结果将保存到常规化参数张量的对应元素之中。
__kernel void UpdateBatchOptionsAdam(__global double *options, ///<[in,out] Options matrix m*9, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer const double l, ///< Learning rates const double b1, ///< First momentum multiplier const double b2 ///< Second momentum multiplier ) { const int n=get_global_id(0); const int shift=n*9; double grad=matrix_g[n]; //--- double2 mt=b1*(double2)(options[shift+5],options[shift+6])+(1-b1)*(double2)(grad*options[shift+2],grad); double2 vt=b2*(double2)(options[shift+5],options[shift+6])+(1-b2)*pow((double2)(grad*options[shift+2],grad),2); double2 delta=l*mt/sqrt(vt+1.0e-8); if(isnan(delta.s0) || isnan(delta.s1)) return; double2 weight=clamp((double2)(options[shift+3],options[shift+4])+delta,-MAX_WEIGHT,MAX_WEIGHT); //--- if(!isnan(weight.s0) && !isnan(weight.s1)) { options[shift+3]=weight.s0; options[shift+4]=weight.s1; options[shift+5]=mt.s0; options[shift+6]=mt.s1; options[shift+7]=vt.s0; options[shift+8]=vt.s1; } };
为了从主程序启动内核,我们来创建 CNeuronBatchNormOCL::updateInputWeights 方法。 该方法在参数中接收一个指向神经网络前一层的指针。 其实这个指针在方法算法中不会用到,只是为了符合父类的继承方法而予以保留。
在方法的开头,检查收到的指针和指向 OpenCL 对象指针的有效性。 与之前研究过的 CNeuronBatchNormOCL::calcInputGradients 方法一样,检查批次尺寸和参数缓冲区的有效性。 将参数缓冲区的内容加载到显卡内存之中。 线程数量应设置为与层中的神经元数量相等。
甚至,该算法可以遵循两个选项,具体则取决于指定的优化方法。 传递内核所需的初始参数,并重启执行。
无论参数采用何种优化方法,计算常规化参数缓冲区的更新内容,之后将缓冲区从显卡内存中移除。
bool CNeuronBatchNormOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); //--- if(optimization==SGD) { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_learning_rates,eta)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_momentum,alpha)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsMomentum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsMomentum %d",GetLastError()); return false; } } else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_l,lr)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b2,b2)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsAdam,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsAdam %d",GetLastError()); return false; } } //--- if(!BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
操作成功完成后,以结果 true 退出方法。
缓冲区替换方法在上一篇文章中有详述,所以我认为它们应该不会造成任何障碍。 这也涉及文件操作(保存和加载已训练的神经网络)。
附件中提供了所有类及其方法的完整代码。
2.4. 神经网络基类的变化
再次,创建一个新类之后,我们将其集成到神经网络的一般结构当中。 首先,我们为新类创建一个标识符。
#define defNeuronBatchNormOCL 0x7891 ///<Batchnorm neuron OpenCL \details Identified class #CNeuronBatchNormOCL
接下来,定义常量宏,从而可操控新内核。
#define def_k_BatchFeedForward 24 ///< Index of the kernel for Batch Normalization Feed Forward process (#CNeuronBathcNormOCL) #define def_k_bff_inputs 0 ///< Inputs data tensor #define def_k_bff_options 1 ///< Tensor of variables #define def_k_bff_output 2 ///< Tensor of output data #define def_k_bff_batch 3 ///< Batch size #define def_k_bff_optimization 4 ///< Optimization type #define def_k_bff_activation 5 ///< Activation type //--- #define def_k_CalcHiddenGradientBatch 25 ///< Index of the Kernel of the Batch neuron to transfer gradient to previous layer (#CNeuronBatchNormOCL) #define def_k_bchg_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_bchg_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_bchg_matrix_i 2 ///<[in] Tensor of previous layer output #define def_k_bchg_matrix_ig 3 ///<[out] Tensor of gradients at previous layer #define def_k_bchg_activation 4 ///< Activation type (#ENUM_ACTIVATION) #define def_k_bchg_batch 5 ///< Batch size #define def_k_bchg_optimization 6 ///< Optimization type //--- #define def_k_UpdateBatchOptionsMomentum 26 ///< Index of the kernel for Describe the process of SGD optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buom_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buom_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buom_learning_rates 2 ///< Learning rates #define def_k_buom_momentum 3 ///< Momentum multiplier //--- #define def_k_UpdateBatchOptionsAdam 27 ///< Index of the kernel for Describe the process of Adam optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buoa_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buoa_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buoa_l 2 ///< Learning rates #define def_k_buoa_b1 3 ///< First momentum multiplier #define def_k_buoa_b2 4 ///< Second momentum multiplier
在神经网络构造函数 CNet::CNet 当中,我们添加创建新类对象和初始化新内核的模块(所有更改在代码中均以高亮显示)。
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
................
................
................
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
................
................
................
CNeuronBatchNormOCL *batch=NULL;
switch(desc.type)
{
................
................
................
................
//---
case defNeuronBatchNormOCL:
batch=new CNeuronBatchNormOCL();
if(CheckPointer(batch)==POINTER_INVALID)
{
delete temp;
return;
}
if(!batch.Init(outputs,0,opencl,desc.count,desc.window,desc.optimization))
{
delete batch;
delete temp;
return;
}
batch.SetActivationFunction(desc.activation);
if(!temp.Add(batch))
{
delete batch;
delete temp;
return;
}
batch=NULL;
break;
//---
default:
return;
break;
}
}
................
................
................
................
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(28);
................
................
................
................
opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward");
opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath");
opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum");
opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam");
//---
return;
}
类似地,在加载预训练神经网络时启动新内核。
bool CNet::Load(string file_name,double &error,double &undefine,double &forecast,datetime &time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return false; //--- ................ ................ ................ //--- if(CheckPointer(opencl)==POINTER_INVALID) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; else { //--- create kernels opencl.SetKernelsCount(28); ................ ................ ................ opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward"); opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath"); opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum"); opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam"); } } ................ ................ ................ ................ ................ }
在加载预训练神经网络的方法中添加一种新型神经元。
bool CLayer::Load(const int file_handle) { iFileHandle=file_handle; if(!CArrayObj::Load(file_handle)) return false; if(CheckPointer(m_data[0])==POINTER_INVALID) return false; //--- CNeuronBaseOCL *ocl=NULL; CNeuronBase *cpu=NULL; switch(m_data[0].Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: ocl=m_data[0]; iOutputs=ocl.getConnections(); break; default: cpu=m_data[0]; iOutputs=cpu.getConnections().Total(); break; } //--- return true; }
类似地,我们在 CNeuronBaseOCL 基类的调度程序方法中添加一种新型神经元。
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- ................ ................ ................ CNeuronBatchNormOCL *batch=NULL; switch(TargetObject.Type()) { ................ ................ ................ case defNeuronBatchNormOCL: batch=TargetObject; temp=GetPointer(this); return batch.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
附件中提供了所有类及其方法的完整代码。
3. 测试
我们继续测试先前所创建智能交易系统中的新类,其生成的可比较数据能用来评估单个元素的性能。 我们测试基于第十二篇文章中的智能交易系统的常规化方法,将舍弃替换为批次常规化。 新智能交易系统的神经网络结构如下所示。 在此,学习率从 0.000001 增加到 0.001。
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*24; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=None; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
EA 基于 EURUSD,H1 时间帧进行了测试。 与之前的测试类似,将 20 根最新烛条的数据输入到神经网络之中。
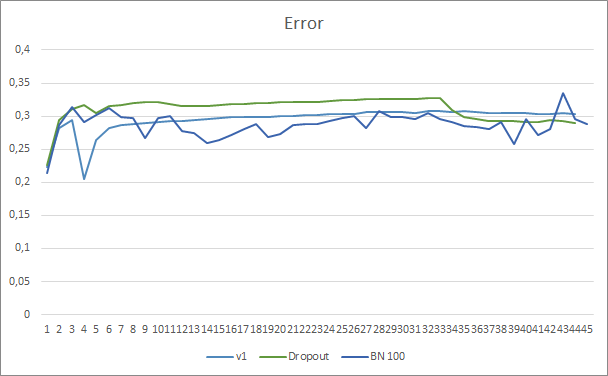
神经网络预测误差展示示,采用批次常规化的 EA,其图型不太平滑,这可能是由于学习率急剧增加造成的。 然而,几乎贯穿整个测试过程,预测误差都低于之前的测试。
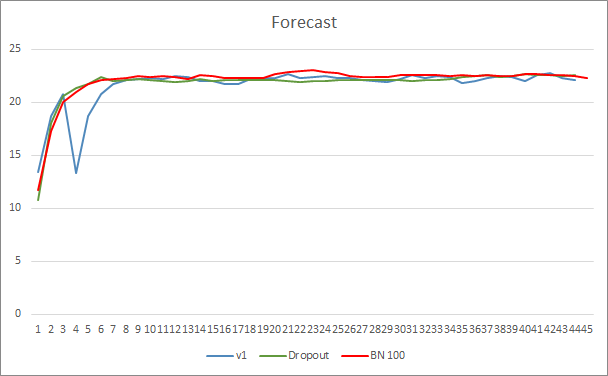
所有三款智能交易系统的预测命中图型都非常接近,因此我们不能断定它们中的哪一个更好。
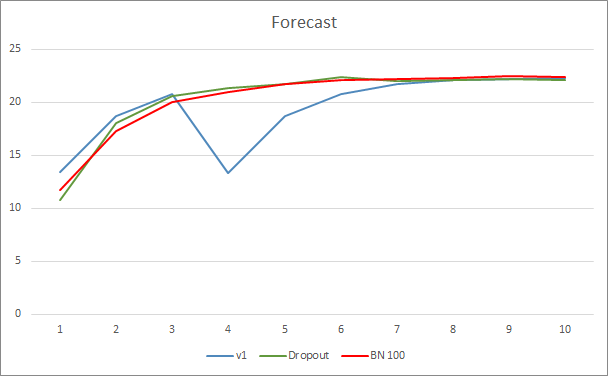
结束语
在本文中,我们继续研究了旨在提高神经网络收敛性的方法,并在我们的函数库中添加了批次常规化类。 测试已表明,采用这种方法可以减少神经网络的误差,并提高学习率。
参考
- 神经网络变得轻松
- 神经网络变得轻松(第二部分):网络训练和测试
- 神经网络变得轻松(第三部分):卷积网络
- 神经网络变得轻松(第四部分):循环网络
- 神经网络变得轻松(第五部分):OpenCL 中的多线程计算
- 神经网络变得轻松(第六部分):神经网络学习率实验
- 神经网络变得轻松(第七部分):自适应优化方法
- 神经网络变得轻松(第八部分):关注机制
- 神经网络变得轻松(第九部分):操作归档
- 神经网络变得轻松(第十部分):多目击者关注
- 神经网络变得轻松(第十一部分):自 GPT 获取
- 神经网络变得轻松(第十二部分):舍弃
- 批次常规化:通过减少内部协变量偏移来加速深度网络训练
- 层常规化
本文中用到的程序
| # | 发行 | 类型 | 说明 |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH_b.mq5 | 智能交易系统 | 一款含有分类神经网络(输出层有 3 个神经元)的智能交易系统,采用 GTP 架构,有 5 个关注层 + BatchNorm |
| 2 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 3 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
| 4 | NN.chm | HTML 帮助 | 一个编译后的函数库帮助 CHM 文件。 |









