内容

1. 概述
2. 理论基础
3. 初级理论
• 3.1. 组合概率
• 3.2. 伯努利（Bernoulli）方案
4. 数理统计基础
5. 在初级理论框架内应用数理统计的示例
• 5.1. 参数点估值
• 5.2. 检验统计假设
6. 结束语
7. 附带文件
   

1.概述

交易总是需要在面对不确定性时做出决定。 这意味着在做出这些决策时，其结局并不十分明朗。 如此看出建立数学模型的理论方法的重要性，它能够令我们以有意义的方式描述这种情况。 我想强调两种方法：概率论和博弈论。 有时，在与概率方法相关的主题中，它们经常被组合在一起作为“与自然演化博弈”的理论。 这清楚地表明存在两种不同类型的不确定性。 第一种（概率）通常与自然现象有关。 第二种（纯游戏相关）则与其他主体（个人或社区）的活动相关联。 博弈的不确定性在理论上更难处理。 有时，这些不确定性甚至被称为“坏”和“好”。 在理解初级博弈相关的不确定性进展时，经常会关联到将其降解为概率形式。

就金融市场而言，自然演化博弈的不确定性显然更为重要，因为人们的活动于此是关键因素。 此处，概率模型的变换通常是基于参考大量参与者，其中每位参与者个体对价格变化的影响很小。 在某种程度上，这与统计物理学中运用的方法类似，而这导致了一门叫做经济物理学的科学方法的出现。

事实上，这种变换的话题非常有趣，不平凡，值得更详细的研究。 希望有一天，相关文章能出现在我们的论坛上。 在这篇文章中，我们将看到概率论和数理统计的基础。

2. 理论基础

概率论的建立基于一个称为Kolmogorov 公理的形式系统。 我不会深入解释什么是“形式系统”，以及如何正确理解数学公理方法，因为这些都属于数理逻辑领域，是非常复杂的问题。 取而代之，我将集中讨论概率论的基本对象 − 概率空间。 它由 一个样本空间、事件集合，和这些事件的概率组成。 我们来更详尽地研究一下：

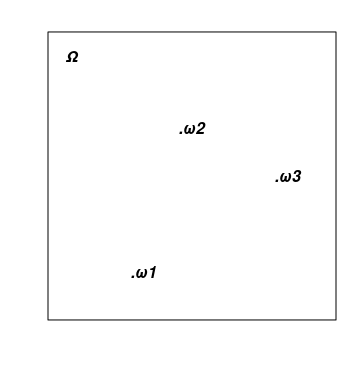
1) 样本空间是随机实验所有可能结果的集合。 它通常用大写的“欧米茄”希腊字母 – Ω 表示，并在图像上刻画为一个图形。 初级事件（采样点）通常用小写的 “欧米茄”希腊字母 − О 表示，并在图像上刻画为一个点。 描述抛硬币结果的最简单标准示例：Ω={ω1, ω2}，其中 ω1=H，且 ω2=T 表示硬币的正面或反面，而花括号表示其元素枚举给出的集合。

下图显示了一个抽象的 Ω，其为一个矩形，以及若干属于它的点 − 基本点：Ω1，Ω2 和 ω3。

2) 随机事件集合。 每个这样的事件都是一个初级事件集合（所有 Ω 基本事件的子集）。 事件集合包括一个空集 ∅={}（一个永远不会发生的事件），和整个 Ω 集（一个总会发生的事件）。 集合中两个事件的组合（和交集）也应属于集合。 在数理中，这样的集合通常称为集合代数。 上面的硬币例子有四个事件: {}=∅,  {H}, {T} 和 {H,T}=Ω。 （自测问题：一个初级事件可以被视为随机事件的一个例子吗？）

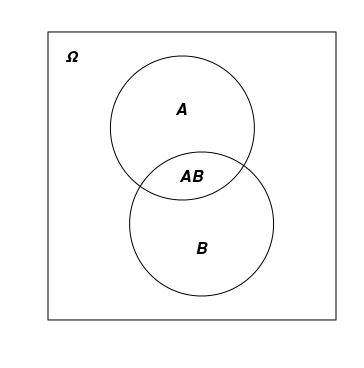
随机事件通常用大写拉丁字母表示：A，B，C，…，并在图像中刻画为位于 Ω 内的形状。 事件的组合和相交会以不同的方式表示。 有时，一个条目类似于普通数值变量加法和乘法: АВ 和 А+В，而有时会用到 ∩ 和 ∪符号: А∩В 和 А∪В。

下图将 Ω 显示为一个矩形和两个相交的 А 和 В 事件。

3) 概率是一个数值函数 P=P(A) 匹配于实数范围从 0 到1 的每个随机事件 A。 P(Ω)=1 和 P(∅)=0。 此外，满足可加性规则：如果 A 事件是一个非重叠 B 和 C 事件的组合，则 P(A)=P(B)+P(C)。 除“概率”项之外，P() 函数应用 “Ω 的概率分布”（或简单地说“Ω 分布”）。 不要把这个概念与类似的“随机变量分布函数”概念混淆。 它们彼此相关，但仍有区别。 前者是把一个数值与集合匹配的函数，后者只是一个数值与数值匹配的普通数值函数。

目前尚不清楚如何在图像中刻画概率分布，但直观地可以将其比作单位质量在 Ω 体积上的分布。 在这个比较中，一个事件是体积的一部分，而概率是这个体积部分中质量的份额。

所有其他概率论概念都是从这些概念中衍生出来的。 我们在这里强调概率相关性（独立性）的一个非常重要的概念。 为此，我将引入A 事件条件概率介入 B 事件执行的概念，P(B)>0。 它表示为 P(A|B)，根据定义，P(A|B)=P(AB)/P(B) （如您所记，AB 是指 A 和 B 事件的交集）。 根据定义，A 事件在某些条件概率下被视为独立于 B 事件，在 B 事件发生期间，它等于概率：P(A|B)=P(A)。 如果我们使用条件概率表达式，独立性的定义可以改写如下：P(A)P(B)=P(AB)。 如果不满足这个等式，则 A 事件可称作依赖于 B 事件。

直观地说，独立性意味着已知 B 事件的发生不会改变与 A 事件相关联的不确定性。 相反，依赖性意味着 B 事件的执行会携带有关 A 事件的信息。 在 Claude Shannon 的信息论里，为这种直觉理解给出了精确表述。

初级概率论通常被单独强调。 初级理论与非初级理论的区别在于，它研究的是由有限个元素组成的初级事件集合。 据此，随机事件的集合也是有限的（自测问题：为什么这是真的？）。 这一理论早在科尔莫戈洛夫公理之前就已发展起来了，且实际上并不需要它。 本文的其余部分将集中讨论这部分理论。 非初级理论将在下一篇文章中加以讨论。

3. 初级理论

鉴于初级结果的数量有限，我们可以简单地设置只包含一个初级事件（单元集合）的事件概率。 我们只需要确保所有这些概率之和等于 1。 任何事件发生的概率都等于这些概率之和。 这些初始概率不必相等，但我们将从这些模型开始，这些模型通常被归纳为“组合概率”。

3.1. 组合概率

设 Ω完全由 N 初级结果组成，那么若包含它们中的 m 数量的结果，则它们的事件概率等于 m/N。 此处的概率计算包括选项数量在内。 作为规则，需用组合方法对付它，故此得名。 以下是一些示例：

示例 1. 假设我们有 n 个多种物品。 那么有多少种不同的方式安置它们（排列）？ 答案: n!=1*2*3*....*(n-1)*n 种方式。 每一种方式都被称为置换，且每一种置换都是一个初级事件。 因此，N=n!，且由 m 个排列组成的事件概率是 m/n! (m/N=m/n!)。

我们来解决一个简单的问题：一个给定对象经随机排列后，定义其处于第一个位置的概率。 如果所选项目占据了第一个位置，则剩余的 n-1 个项目可以放在剩余的 n-1 的位置上，可有 (n-1)! 种方式。 故此，m=(n-1)!，也就是说期望的概率等于 m/N=m/n!=(n-1)!/n!=1/n。

示例 2. 我们已有 n 个多种物品。 我们可从它们当中分离出多少个不同的 k (k<=n) 项目集合？ 这里有两个可能的选择，这取决于我们是否考虑两个集合，只是项目的顺序不同。 如果是，那么答案为 n!/(n-k)! 个集合。 如果非，则 k! 数倍少于: n!/((n-k)!*k!)。 考虑顺序的集合称为分配，不考虑顺序的集合称为组合。 分配数字创建，已知也称为二项式系数方程，应用特殊符号 − 下图中显示了两个选项。

因此，如果集合中元素的顺序不重要，我们可用组合作为一个初级事件集合来解决问题。 如果顺序很重要，则应使用分配。

示例 3. 我们来研究一个导致所谓超几何分布的重要例子。 假设每个 n 项都被标记为 “好” 或 “坏”。 设 b，b⋜n 项为“坏”，则剩余的 n-b 项为“好”。 选择一个 k 元素集合，且不考虑它们的顺序（组合）。 我们的集合中确切包含 x “坏”项的概率是多少？ 通过计算包括匹配组合的数量在内来解决这个问题。 答案相当繁琐，最好记下下图中所示的组合数字，其中期望的概率为 p，并由 x，n，b 和 k 表达。

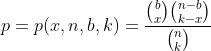
这个示例非常适合于理解所引入的“随机变量”概念背后的逻辑（下一篇文章将更详细地讨论它）。 很可能的结果是，为了解决与计算事件概率有关的特定问题，掌握 x, n, b 和 k 的知识就足够了，而关于整个事件初始集合的完整数据是多余的。 然后通过舍弃不必要的信息来简化原始模型颇具意义。 我们如下继续：

• n, b 和 k 假设为固定参数。
• 取代 Ω 样本空间，基于它建造一个新的 Ωх={0, 1, ..., k}。 新空间大概由 х 个值组成。
• 将每个 {х} 事件（由一个初级事件组成）与上面所示的超几何分布方程指定的概率相匹配。

产生的对象称为“离散随机变量”，其可能值的超几何分布为 Ωх。

3.2. 伯努利（Bernoulli）方案

这是另一个来自初级概率论领域的著名模型。 其示例通常涉及连续抛硬币结果建模，但我会以一种更正式的方式构建蓝图。

假设我们有一个正整数 n 和一对非负实数 p 和 q，因此 p+q=1。 Ω 样本空间由精确长度为 n 的单词组成，其中仅允许 H 和 T 个字母 (H − 正面， T − 反面)。 一个由一个初级事件组成的事件概率由这个方程确定 pu({w})=p^nh*q^nt，其中 w 是一个单词，而 nh 和 nt, nh+nt=n 相应代表 H 和 T 个数量的字母。

很容易看出，与组合概率相比，初始概率通常彼此不相等（只有当 p=q=0.5 时，它们才是相似的）。

我们研究一下 n=2 的例子。 在此情况下，Ω={HH, HT, TH, TT}。 此处的初级数量等于 4，而随机事件的数量是 16。 （自测问题：从伯努利方案的 n 导出描述初级事件数量，和所有随机事件数量相关性方程的一般形式）。

我们来研究 "H"=comes first {HH, HT} 事件。 其概率为 pq+p^2=p。 这同样适用于任何允许我们将 p 参数作为“每次掷骰都得到反面可能性”的说法。 现在，我们检查是否 А="H 为第二"={HH, TH} 事件独立于 В="H 为第一"={HH, HT} 事件。 我们用独立性定义 − АВ={HH}, P(A)=p, P(B)=p 和 P(AB)=p^2 的交集。 由于、 P(A)P(B)=p*p=p^2=P(AB)，事件是独立的。

关于每一次掷骰结果的概率，及其独立性的陈述对所有 n>2 都是正确的。

我们可以用其他方式指定概率，也许这会导致不存在相等的概率，或者导致掷骰结果的依赖性。 此处的重点是伯努利方案不是描述事件序列的唯一有效模型，我们不应局限于此。

现在我们来计算一个事件概率，其中 H 发生的次数正好是 k 次，或者（不太正式）掷骰 n 次出现正面的概率等于 k 次。 这个问题的答案可以在下面的图中找到。 pb 表示期望的概率，取决于 k, n, p 和 q。

考虑另一个例子，展示了二项分布和上面所研究的超几何分布之间的关系。 它本身及其在数理统计中的应用都很重要 (费舍尔（Fisher）精确检验)。 从数学的角度来看，这个问题是相当复杂和有意义的。 我们一点点地强调所有的推理。

• 基于伯努利方案的 Ω 样本空间，构建一个新的 − Ω1 仅包含单词，其中 H 精确出现了 b 次。
• 由于在 Ω1 当中的任意 A 事件也是 Ω 当中的一个事件，P(A) 即是为它定义的概率。 基于此事实，我们根据方程 P1(A)=P(A)/Р(Ω1)为 Ω1 引入 P1 概率。 事实上，这里用的是条件概率方程 P1(A)=P(A|О1)。
• 现在研究来自 Ω1 的"一个长度为 k 的单词的后缀正好包含 x 个 H 个字母"的事件概率 P1()。 结果表明，这个概率正是由上面提供的超几何分布方程设定的。 非常值得注意的是，方程不影响 p 参数。

4. 数理统计基础

数理统计和概率论的区别通常被解释为它们解决的问题类型的不同。 在概率论中，通常假设概率模型是完全已知的，并据此得出一些结论。 在数理统计中，对于模型的认知是不完整的，但有一些附加的信息能以实验数据的形式帮助改进模型。 因此，上一章讨论的所有问题都是概率论的问题。

我刚才提供的数理统计的定义可以认为是传统的。 还有另一种更现代的数理统计定义方法。 它可以被定义为决策论的一部分。 在这种情况下，重点是构造决策规则，在误差平均代价最小化的意义上是最优的。 在此，机器学习方法有很强的收敛性。 一个与它们显著区别在于，在数理统计中，所应用数学模型的类型会得到相当清晰的判断（例如，在未知参数的精度范围内）。 在机器学习中，不确定性通常也会扩展到模型类型。

现在我们来研究传统意义上的数理统计的样本问题。

5. 在初级理论框架内应用数理统计的示例

有两种类型的问题 − 估算参数和检查假设。

我们从参数点估值开始。 它假设概率模型中存在任何数值（非随机、确定性）变量。 它们的确切数值是未知的，但我们可以利用随机实验获得的数据来计算它们的近似值。

5.1. 参数点估值

此处最普遍的方法是使用最大似然估值方法。 如果一些 ω 初级事件已知是随机实验的结果，那么似然函数就是 {ω} 事件的概率（仅由这个初级事件组成）。 它被称为函数，在于它依赖于模型参数值。 最大似然估值（MLE）是该函数达到最大值的参数值。

除了 MLE 之外，可能还有多种不同的参数估值，但正如数理统计所证明的那样，MLE 在精确度方面是最好的。 在下一篇专门讨论随机变量的文章之前，我会在此解释“精度”一词的含义。 无论如何，我们应当记住，统计估值几乎总是与参数的真实值不同。 因此，区分它们是非常重要的。 例如，伯努利方案中事件的概率及其以频率形式的估值。

我们继续使用示例计算 MLE。

示例 1. 估计超几何分布中的 b 参数。 这是一批工件 n=1000 片。 在检查了其中的 k=20 之后，检测到一个缺陷工件：x=1。 估算整批中有缺陷的工件数量。

以下是用 Python 编写的 hyperg_be.py 脚本，可通过所有可能选项的枚举 b 来解决这个问题。 答案是 be 估值，其中由超几何分布方程确定的似然值最大。

from scipy.stats import hypergeom

n = 1000
k = 20
x = 1
lhx = 0.0
be = 0
for b in range(x, n - k + x):
    lh = hypergeom.pmf(x, n, b, k)
    if lh > lhx:
        be = b
        lhx = lh
        
print("be =",be)

答案: be = 50，这是期望的（每 20 个工件）。

示例 2. 估算超几何分布里的 n 参数。 需要估算水体中的鱼类数量。 为了做到这一点，b=50 的鱼用网捕捉，标记后再放生。 之后，捕获 k=55 条鱼，其中 x=3 条带有标记。

以下是用 Python 编写的 hyperg_ne.py 脚本，它通过可能选项的枚举 n 来解决这个问题。 答案是 ne 为估算的最大概率值。 一点细微差别是 n 可能数值的理论范围是从 50+(55-3)=102 到无穷大。 这可能导致无休止的枚举循环。 但结果则是似然函数一直增长，直到某个 n 值。 然后开始递减，直至趋于零。 相应地，答案是第一个 ne 值，其似然函数值大于其所在 ne+1 处的值。

from scipy.stats import hypergeom

b = 50
k = 55
x = 3
lh0 = 0.0
ne = b + k - x - 1
while True:
    lh = hypergeom.pmf(x, ne+1, b, k)
    if lh < lh0:
        break
    else:
        lh0 = lh
        ne += 1
        
print("ne =",ne)

答案: ne = 916，这也是期望的 (ne/b 大致相等 k/x，故结果是 ne 大致相等 b*k/x)。

下面所有的例子都与伯努利方案或其修订版有关。 对这个模型的传统交易演绎是将其与离散化的资产价格相匹配。 例如，可以用 renko 或点数，以及示意表图来获得这种表现。

我们沿用这个传统方法。 替换 H 和 T 字母，我们打算看看 1 和 -1 数字的序列，显然这与不连续的价格阶梯（分别是上涨和下跌）相对应。 一般来说，价格阶梯可以定义为在价格网格上达到一个新的水平。 这些水平网格通常是这样定义的，从而每层与其相邻低居之间的差距或关系保持不变。我将使用第二种方法。 这种方法的缺点是不能用于负价格的资产，而优点是不需要为每种资产单独选择步长。 另外，在选择零轴时也有一些随意性。 其所扮演的角色将取决于那些被离散化题材的第一个价格。

下面是一个简单的脚本，它以给定的百分比步长在给定的区间离散价格。Discr.mqh 文件只包含 setmv() 函数，其内实际生成离散化价格。出于简单起见，只取分钟柱线的开盘价作为起始价。

// 构造走势的离散 mv[] 数组
// 以指定的百分比步长，在指定的时间区间
void setmv(int& mv[], datetime t1, datetime t2, double dpr)
{
  int ND = 1000;
  ArrayResize(mv, 0, ND);
// 获取价格历史记录
  double price[];
  int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price);
  if(nprice < 2)
  {
    Print("not enough price history");
    return;
  }
// 构造 mv[]
  int lvl = 0, dlvl, nmv = 0, dmv;
  double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr);
  for(int i = 1; i < nprice; ++i)
  {
    dlvl = (int)((log(price[i]) - lp0) / lstep - lvl);
    if(dlvl == 0) continue;
    lvl += dlvl;
    dmv = 1;
    if(dlvl < 0)
    {
      dmv = -1;
      dlvl = -dlvl;
    }
    ArrayResize(mv, nmv + dlvl, ND);
    for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv;
    nmv += dlvl;
  }
}

discret_prices.mq5 脚本显示的结果为 1 和 -1 的序列，以及起始价格的离散模拟图。

#include <Discr.mqh>
#include <Graphics\Graphic.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 所研究时间区间的开始
input datetime tstop = D'2020.06.20 00:00';   // 所研究时间区间的结束
input double   dprcnt = 0.5;                  // 价格离散化步长百分比
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[], nmv;
  setmv(mv, tstart, tstop, dprcnt);
  nmv = ArraySize(mv);
  if(nmv < 1)
  {
    Print("not enough moves");
    return;
  }
// 显示 mv[] 为 1 和 -1 的序列
  string res = (string)mv[0];
  for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i];
  Print(res);
// 显示 mv[] 累加汇总图表
  ChartSetInteger(0, CHART_SHOW, false);
  CGraphic graphic;
  graphic.Create(0, "G", 0, 0, 0, 750, 350);
  double x[], y[];
  ArrayResize(x, nmv + 1);
  ArrayResize(y, nmv + 1);
  x[0] = y[0] = 0.0;
  for(int i = 1; i <= nmv; ++i)
  {
    x[i] = i;
    y[i] = y[i-1] + mv[i-1];
  }
  ArrayPrint(x);
  ArrayPrint(y);
  graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices");
  graphic.CurvePlotAll();
  graphic.Update();
  Sleep(30000);
  ChartSetInteger(0, CHART_SHOW, true);
  graphic.Destroy();
}

在下面的所有例子中，我将选用 EURUSD 价格离散化的结果，从 2020 年 5 月 20 日到 6 月 20 日，增量为 0.5%。 结果是如下的离散足迹序列: 1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1. 为了更清楚起见，下面显示了原始价格，及其离散模拟图。

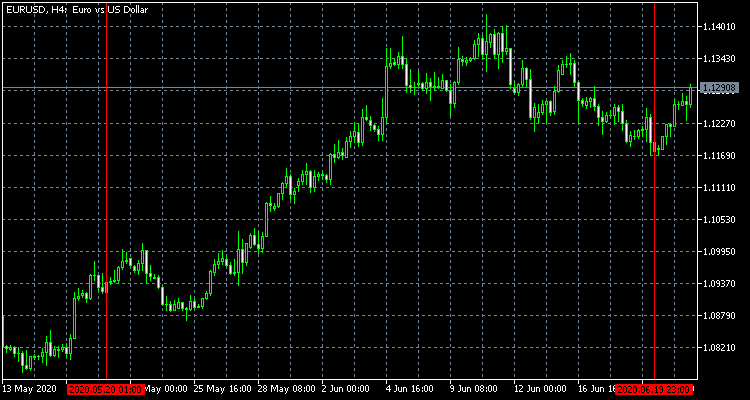
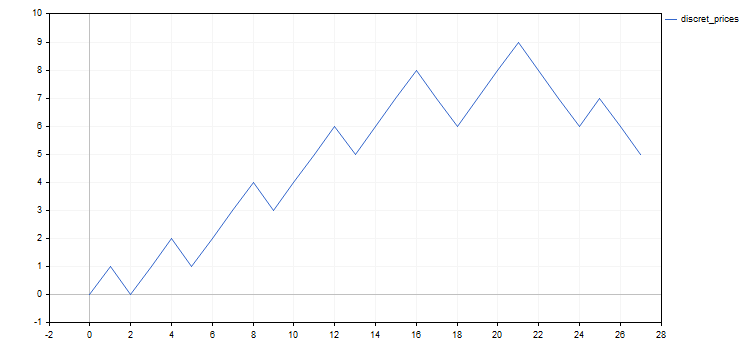
除了研究离散化价格的行为，可能还有其他方式来应用伯努利方案或其修订版。 我们指出其中与交易有关的两个。

1. 交易结果中，成交带有固定的的止损和止盈，及交易量等级。 一系列交易的所有利润大致相等，亏损也是如此。 故此，盈利概率是描述交易结果的一个充分参数。 例如，我们可以提出一个问题，即在现有的成交序列中，盈利的概率是否足够高。 
2. 选择要投资的资产。 假设我们在区间伊始有大量的投资方法可供选择。 其中任何一个，都有一定的概率，最终都可能导致投资基金的彻底亏损。 如果有选择资产的方法，那么可能提出疑问：所择资产与规避资产之间最终导致破产概率的差异。
   

我们回到示例。

示例 3. 估算伯努利方案中的 p 参数。 这是罕见案例，可以在纸上解决的问题。 似然函数如下：p^nup*(1-p)^ndn。 取 p 的导数，并令其等于零，获得估算 р 的期望值作为频率: pe=nup/(nup+ndn)=nup/nmv。 通常情况下，执行的搜索不是针对似然函数的最大值，而是针对其对数，这要容易得多。 答案是一样的，因为对数是严格递增的函数，并且在相同的参数值下达到最大值。 以下是计算估值的 p_model.mq5 脚本。

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 所研究时间区间的开始
input datetime tstop = D'2020.06.20 00:00';   // 所研究时间区间的结束
input double   dprcnt = 0.5;                  // 价格离散化步长百分比
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 1)
  {
    Print("not enough moves");
    return;
  }
  double pe = calcpe(mv);
  Print("pe=", pe);
}
//+------------------------------------------------------------------+
// 计算概率估值
double calcpe(int& mv[])
{
  int nmv = ArraySize(mv);
  if(nmv < 1) return 0.0;
  int nup = 0;
  for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup;
  return ((double)nup) / nmv;
}

答案: pe = 0.59 (四舍五入)

示例 4. 伯努利方案修订版的参数估值。 正如我在上面所写的，伯努利方案可以很好地根据我们的建模目的进行更改。 我们来研究一个可能的修改选项。

也许，最简单的选择是将走势序列切分成两个更小的序列，一个接着一个，并与伯努利方案及其参数相对应: n1, p1, n2=n-n1 和 p2，其中 n 是累积序列的长度。
因此，需要估算三个参数 − n1, p1 和 p2。 最大化对数似然函数 p1 和 p2，令我们可以通过 n1 来分析表达它们。 n1 的估值可简单地将 p1 和 p2 代入对数似然方程求解得到。 下面是计算参数估值的 p1p2_model.mq5 脚本。

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 所研究时间区间的开始
input datetime tstop = D'2020.06.20 00:00';   // 所研究时间区间的结束
input double   dprcnt = 0.5;                  // 价格离散化步长百分比
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  int n1e;
  calc_n1e_p1e_p2e(mv, n1e, p1e, p2e);
  Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// 计算概率估值
void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e)
{
  n1e = 0;
  p1e = p2e = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  n1e = 1;
  double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2;
  for(int n1 = 2; n1 < nmv; ++n1)
  {
    llh = llhx_n1(mv, n1, p1, p2);
    if(llh > llhx)
    {
      llhx = llh;
      n1e = n1;
      p1e = p1;
      p2e = p2;
    }
  }
}
//+------------------------------------------------------------------+
// 对数似然函数最大值取决于 n1
double llhx_n1(int& mv[], int n1, double& p1, double& p2)
{
  p1 = p2 = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0;
  int nu1 = 0, nu2 = 0;
  for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1;
  for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2;
  double l = 0.0;
  if(nu1 > 0)
  {
    p1 = ((double)nu1) / n1;
    l += nu1 * log(p1);
  }
  if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1);
  if(nu2 > 0)
  {
    p2 = ((double)nu2) / (nmv - n1);
    l += nu2 * log(p2);
  }
  if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1));
  return l;
}

答案: n1e = 21; p1e = 0.71; p2e = 0.17 (数字四舍五入)。 这似乎很明显 − 我们的模型行情的末尾“检测”到价格方向的变化（或调整）。 这提供了建议，针对这种情况，过渡到更复杂的模型并非徒劳。

示例 5. 在前面的示例中，走势上移的概率取决于它的数字（在时间上）。 我们来研究一下伯努利方案的另一个修订版，其中这个概率取决于之前的走势本身。 我们来构造一个模型，它是最简单的两个状态 Markov 链 的一个例子。

假设给走势编号，从 0 到 n。 若走势为零，走势上移的概率简单地设置为等于 0.5，因为没有以前的走势。 对于其他位置，如果之前的走势向上，上移的概率等于 p1；如果之前的走势是向下的话，则为 p2。 在这两种情况下走势向下的概率等于 q1=1-p1，相应地 q2=1-p2。 例如，一个事件有一个初级事件的概率 "向下-向上-向上-向下" 是 0.5*p2*p1*q1。

我们已得到了一个含有两个参数的模型，可以用极大似然估值。 此处的所有计算都可以在纸上进行，特别是当我们最大化对数似然函数时。 与伯努利方案一样，答案归结为频率。 上行走势之后发生下行走势的次数可设为 nud (u − 上行, d − 下行)。 以类似的方式，引入 nuu, ndd 和 ndu。 估算 p1 和 p2 可由 p1e 和 p2e 表示。 然后利用这些方程得到这些估值 p1e=nuu/(nuu+nud) 和 p2e=ndu/(ndu+ndd)。

下面是计算这些估值的 markov_model.mq5 脚本。

#include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 所研究时间区间的开始
input datetime tstop = D'2020.06.20 00:00';   // 所研究时间区间的结束
input double   dprcnt = 0.5;                  // 价格离散化步长百分比
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  calcpes(mv, p1e, p2e);
  Print("p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// 计算概率估值
void calcpes(int& mv[], double& p1e, double& p2e)
{
  p1e = p2e = 0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd;
  for(int i = 0; i < nmv - 1; ++i)
    if(mv[i] > 0)
    {
      if(mv[i + 1] > 0) ++nuu;
      else ++nud;
    }
    else
    {
      if(mv[i + 1] > 0) ++ndu;
      else ++ndd;
    }
  nu = nuu + nud;
  nd = ndu + ndd;
  if(nu > 0) p1e = ((double)nuu) / nu;
  if(nd > 0) p2e = ((double)ndu) / nd;
}

答案:  p1e = 0.56; p2e = 0.60 (数字四舍五入)。 两个概率几乎相等，表明相邻走势之间没有相关性。 两个概率都大于 0.5 ，表明此为上升趋势。 两个概率估值都接近于一个更简单模型的概率估值（第三个例子中的简单伯努利方案），这表明在这种特殊情况下，过渡到更复杂模型毫无必要。

5.2. 检验统计假设

在同一样本空间上可以设置不同的概率分布。 猜想是指定分布类型的陈述。 应该有几个猜想（至少两个），因为解决方案应建立在一个猜想优于其他。 如果一个猜想即可唯一断定分布类型，就称之为简单猜想。

我们提供伯努利方案的例子：p 参数等于某个数值  猜想 − 一个简单猜想（只有一个可能的参数值，明确定义了分布），而参数超过指定值的猜想是一个复杂的猜想（可能的参数值是无限的）。

接下来，我们将讨论如何选择两个猜想中的一个。 其中一个称为 null，另一个是备选的。 猜想是用一个统计标准来选择的。 基本上，这只是一个在样本空间内含有 0 和 1 值的函数，其中 0 意味着接受空猜想，而 1 表示接受备选。

因此，我们既可以接受空猜想，也可以拒绝它。 相应地，备选猜想要么被拒绝、要么被接受。 每一个决定都可能是对的、或是错的。 因此，接受这个猜想有四种可能的结果，其中两种是正确的，两种是错误的。

1. 类型 1 错误 − 空猜想的错误否定。
2. 类型 2 错误 − 空猜想的错误接受。

第 1 类和第 2 类错误的概率由 a1 和 a2 表示。 很自然，最好尽可能减少这些可能性。 但不幸的是，这是不可能的。 甚至，通过降低某种类型错误的概率，我们相当期待面临另一类错误发生概率的增加。 这就是为什么通常要在这些错误之间做出某种妥协。

1-a1 被称为测试意义，而 1-a2 叫做它的动力。 测试动力很难计算，尤其是对于复杂的猜想。 因此，通常只用到测试意义。

标准通常基于一个称为检验统计量的数值函数（也定义为基于样本空间）。 它的多个值分为两个区域。 其中一个区域对应于接受空猜想，而另一个区域对应于拒绝。 拒绝空猜想的区域称为临界区。

下面是关于“负优先”猜想的一个重要注释。 这个条件意味着我们应该事先确保两个猜想中的一个得以满足。 粗略地说，如果我们把吉娃娃和其他品种的狗按重量分开，那么我们必须确保我们的天平上总有一只狗（不是大象、老鼠或猫）。 否则，我们的测试就没有意义了。 当计量经济学中所应用的统计条件不准确时，这一原则最常被违反。

下面是伯努利方案检验猜想的例子。

示例 1. 在伯努利方案里检验空猜想 p=p0。 这个猜想很简单。 备选猜想可以是以下两种选项之一（这两种情况都很复杂）。 kup （序列中上行走势的次数）被用作两种情况下的统计标准，尽管临界区域的定义不同。

1. p>p0，临界区域在右边 kup⋝kr
2. p<p0，临界区域在左边 kup⋜kl

kr 和 kl 的具体值可按条件查找，统计概率落入临界区域不会超过所选的 1 类错误概率。 正如我已经说过的，所有这些概率都是依据条件计算出来的，此刻满足空猜想（伯努利分布的参数 p=p0)。

我们在同样的离散价格序列上检验这个猜想，即 p0=0.5。 p0 的值很大，因为它符合“随机游走”（“公平硬币”）猜想。

下面的这个脚本 p0_hypothesis.mq5 验证这个猜想。

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input int    nm = 27;          // 序列中的走势总数
input int    kup = 16;         // 上行走势的数量
input double p0 = 0.5;         // 检查概率值
input double alpha1 = 0.05;    // 类型 1 错误概率
//+------------------------------------------------------------------+
void OnStart()
{
  int kl, kr, er;
  kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er);
  kl=(int)MathQuantileBinomial(alpha1,nm,p0,er);
  Print("kl=", kl, " kup=", kup, " kr=", kr);
  Print("kup<=kl = ", kup<=kl);
  Print("kup>=kr = ", kup>=kr);
}

回应：

示例 2. 假设我们有两个长度为 n1 和 n2 的序列，它们取自两个参数为 p1 和 p2 的伯努利方案。 此处的空假设是在于满足 p1=p2 等式，而可能的备选方案是不同类型的不等式，这里也有两种。 k2 作为所有这些情况下的统计标准 − 两个序列中第二个序列中上行走势的次数，尽管临界区域的定义不同。

• p2>p1，临界区域在右边 k2⋝kr
• p2<p1，临界区域在左边 k2⋜kl

与前一个例子的显著区别，此处我们讨论的并非关于 p1 和 p2 数值的精度，而是关于它们的比率。 临界区域的定义方法与前一个例子相同，但在空猜想下，统计分布是超几何的，而不是二项式的。 在数理统计中，这个标准被称为费舍尔精确检验。

下面是用 Python 编写的解决这个问题的 p1p2_hypothesis.py 脚本，将离散化的价格一分为二。 我把来自上一段落中第四个示例中获得的数据拆分。

from scipy.stats import hypergeom

n1 = 21; n2 = 6
k1 = 15; k2 = 1
alpha1 = 0.05

kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2))
kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2))

print("kl =", kl, " k2 =", k2, " kr =", kr)
print("k2<=kl =", k2<=kl)
print("k2>=kr =", k2>=kr)

 回应：

• kl = 2;  k2 = 2;  kr = 6
• k2<=kl = True
• k2>=kr = False
  

6. 结束语

本文并未涉及到数理统计的重要领域，如描述性统计、区间参数估值、渐近估值和统计学中的贝叶斯方法。 原因是我需要澄清随机变量的概念，从而对其进行有意义的研究。 我决定在下一篇文章中再做这件事，从而令本篇幅足够紧凑。

7. 附件

#	名称	类型	说明
1	hyperg_be.py	Python 脚本	计算 b 超几何分布参数估值。 示例 5.1.1
2	hyperg_ne.py	Python 脚本	计算 n 超几何分布参数估值。 示例 5.1.2
3	Discr.mqh	MQL5 头文件	在所有 MQL5 示例中价格离散化均用到的 setmv()函数文件
4	discret_prices.mq5	MQL5 脚本	执行价格离散化，并以 1 和 -1 序列形式显示结果图表的脚本
5	p_model.mq5	MQL5 脚本	计算伯努利方案中的 p 参数估值。 示例 5.1.3
6	p1p2_model.mq5	MQL5 脚本	计算由两个伯努利方案组成的模型中 n1, p1 和 p2 参数估值。 示例 5.1.4
7	markov_model.mq5	MQL5 脚本	计算 Markov 链中的 p1 和 p2 参数估值。 示例 5.1.5
8	p0_hypothesis.mq5	MQL5 脚本	检验伯努利方案猜想的参数是否等于指定数字。 示例 5.2.1
9	p1p2_hypothesis.py	Python 脚本	费舍尔精确检验。 示例 5.2.2