在本文中，我们将继续研究各种数学表达式解析方法，及其在 MQL 语言中的实现。 在第一部分里，我们研究了递归下降解析器。 这种解析器的主要优点在于用户友好的结构，它与特定的表达式语法直接相关。 但是，在效率和技术功能方面，还有其他类型的解析器值得关注。

解析器采用运算符优先级

我们要研究的下一个解析器类型是优先级解析器。 它们具有更紧凑的实现，因为类方法并非基于语法规则创建的（在这种情况下，每个规则都转换为单独的方法），而是采用更通用的形式，仅考虑运算符的优先级。

在 EBNF 语法说明中，操作的优先级已经以隐式形式出现：其规则执行从低优先级操作到高优先级操作，直至终结实体 — 常量和变量。 这是因为在没有显式括号分组的情况下，优先级判定应是操作执行的顺序。 例如，乘法运算的优先级高于加法的优先级。 但是一元减号优先于乘法。 语法树元素越靠近根部（整个表达式），对其进行评估越靠后。

为了实现解析器，我们需要两个表，每张表的数值与每个操作的优先级相对应。 值越高，优先级越高。

我们有两张表，因为一元和二元运算会在算法中逻辑上分开。 实际上，我们不仅在讨论操作，且在更广泛地讨论有关在表达式中如何找到可作为前缀和后缀的符号（Wikipedia 上有更多关于操作符类型的信息）。

顾名思义，前缀是操作数之前的符号（例如，“!var” 表达式中的 “!”），而中缀是操作数之间的字符（例如，表达式 ”a + b“ 中的 ‘+’）。 还有一些后缀（例如，增量运算符中的一对 “+”，在 MQL 中也可以用 — “i++”），但是我们在表达式中没有用到它们，因此我们先不考虑它们。

除了一元运算符 '!'，'-'，'+' 外，前缀还可以是一个开始括号 '(' — 表示分组的开头；字母或下划线 — 表示标识符的开头；以及数字或句点 “.” — 表示数字常数的开头。

我们讲述 ExpressionPrecedence 类中的表，它继承自某些基于优先级的解析器类。 所有这些解析器将与 Promise 一起操作。

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      static uchar prefixes[128];
      static uchar infixes[128];
      
      static ExpressionPrecedence epinit;
      
      static void initPrecedence()
      {
        // 分组
        prefixes['('] = 9;
  
        // 一元运算符
        prefixes['+'] = 9;
        prefixes['-'] = 9;
        prefixes['!'] = 9;
        
        // 标识符
        prefixes['_'] = 9;
        for(uchar c = 'a'; c <= 'z'; c++)
        {
          prefixes[c] = 9;
        }
        
        // 数字
        prefixes['.'] = 9;
        for(uchar c = '0'; c <= '9'; c++)
        {
          prefixes[c] = 9;
        }
        
        // 运算符
        // infixes['('] = 9; // 此处不将括号用作“函数调用”运算符
        infixes['*'] = 8;
        infixes['/'] = 8;
        infixes['%'] = 8;
        infixes['+'] = 7;
        infixes['-'] = 7;
        infixes['>'] = 6;
        infixes['<'] = 6;
        infixes['='] = 5;
        infixes['!'] = 5;
        infixes['&'] = 4;
        infixes['|'] = 4;
        infixes['?'] = 3;
        infixes[':'] = 2;
        infixes[','] = 1; // 参数列表定界符
      }
  
      ExpressionPrecedence(const bool init)
      {
        initPrecedence();
      }
  
    public:
      ExpressionPrecedence(const string vars = NULL): AbstractExpressionProcessor(vars) {}
      ExpressionPrecedence(VariableTable &vt): AbstractExpressionProcessor(vt) {}
  };
  
  static uchar ExpressionPrecedence::prefixes[128] = {0};
  static uchar ExpressionPrecedence::infixes[128] = {0};
  static ExpressionPrecedence ExpressionPrecedence::epinit(true);

优先级表则按“经济”方式创建，利用 128 个元素的稀疏数组（这已足够了，因为不支持来自其他范围的代码字符）。 在与符号代码相对应的单元格中指定优先级。 因此，可按令牌代码直接寻址来轻松访问优先级。

子类中将使用两个附加的辅助方法，从而可以检查输入字符串中的符号：_lookAhead 仅返回下一个标记（如同向前看）；_matchNext — 如果匹配则读令牌，否则抛出错误。

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      ...
      ushort _lookAhead()
      {
        int i = 1;
        while(_index + i < _length && isspace(_expression[_index + i])) i++;
        if(_index + i < _length)
        {
          return _expression[_index + i];
        }
        return 0;
      }
      
      void _matchNext(ushort c, string message, string context = NULL)
      {
        if(_lookAhead() == c)
        {
          _nextToken();
        }
        else if(!_failed) // prevent chained errors
        {
          error(message, context);
        }
      }
      ...
  };

我们从第一个基于优先级的解析器开始：普拉特解析器。

普拉特解析器 (ExpressionPratt)

普拉特解析器是自上而下的，就像递归下降解析器一样。 这意味着它可递归调用某些方法来分析表达式中的独立构造，。 然而，这些方法很少见。

构造函数和主要的公开 “evaluate” 方法看起来很眼熟。

  class ExpressionPratt: public ExpressionPrecedence
  {
    public:
      ExpressionPratt(const string vars = NULL): ExpressionPrecedence(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionPratt(VariableTable &vt): ExpressionPrecedence(vt) { helper = new ExpressionHelperPromise(&this); }
  
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          return parseExpression();
        }
        return NULL;
      }

新的 parseExpression 方法是普拉特算法的核心。 首先，开始要将当前优先级默认设置为 0，这意味着可以读取任何信号。

      virtual Promise *parseExpression(const int precedence = 0)
      {
        if(_failed) return NULL; // 出错时截断子表达式
      
        _nextToken();
        if(prefixes[(uchar)_token] == 0)
        {
          this.error("Can't parse " + ShortToString(_token), __FUNCTION__);
          return NULL;
        }
        
        Promise *left = _parsePrefix();
        
        while((precedence < infixes[_token]) && !_failed)
        {
          left = _parseInfix(left, infixes[(uchar)_token]);
        }
        
        return left;
      }

该方法的思路很简单：开始解析表达式时，先读取下一个符号，必须是前缀（否则出错），然后将控制权传递给 _parsePrefix 方法，该方法可以读取任何前缀的整体构造。 在此之后，只要下一个符号的优先级高于当前优先级，就将控制权传递给 _parseInfix 方法，该方法可以读取任何 infix 的整体构造。 如此，整个解析器仅包含三个方法。 从某种意义上说，普拉特解析器将表达式表述为由前缀和中缀构造的层次结构。

请注意，如果在中缀表中找不到当前的 _token，则其优先级为零，且 'while' 循环将终止（或根本不会启动）。

_parseInfix 方法的特定功能是，当前的 Promise (left) 对象会在第一个参数中被传递到内部，成为子表达式的一部分，而在该方法的第二个参数里设置允许的最小操作优先级，作为当前中缀令牌的优先级。 该方法返回依据整个子表达式生成的新 Promise 对象。 该对象保存在相同的变量中（之前的 Promise 引用，则会通过新对象的引用字段以某种方式提供）。

我们来研究方法 _parsePrefix 和 _parseInfix 详情。

_parsePrefix 方法期待来自许可前缀的当前令牌，并利用 “switch” 进行处理。 对于开头的括号 '('，调用已熟知的方法 parseExpression 来计算嵌套表达式。 优先级参数则被省略，这意味着从最低的零优先级进行解析（因为它就像方括号中的单独表达式一样）。 一个 “helper” 对象用于 “!”，以便接收逻辑非得下一个片段。 它由 parseExpression 方法读取，但这次会将当前令牌的优先级传递给它。 这意味着取非的片段将在第一个符号之前以低于 “!” 的优先级结束。 例如，如果表达式为 “!a*b”，则 parseExpression 将在读取 “a” 变量后停止，因为乘法 “*” 的优先级低于取非 “!” 的优先级。 一元 '+' 和 '-' 以类似的方式处理，但在这种情况下不使用 “helper”。 对于 “+”，我们只需要让 parseExpression 读取子表达式。 对于 '-'，调用覆盖方法 “minus” 接收结果（您应当记得，结果是 Promise 对象）。

_parsePrefix 方法根据它们是否属于 “isalpha” 类别为所有其他符号排序。 假定字母是标识符的开头，数字或句点是数字的开头。 在所有其他情况下，该方法将返回 NULL。

      Promise *_parsePrefix()
      {
        Promise *result = NULL;
        switch(_token)
        {
          case '(':
            result = parseExpression();
            _match(')', ") expected!", __FUNCTION__);
            break;
          case '!':
            result = helper._negate(parseExpression(prefixes[_token]));
            break;
          case '+':
            result = parseExpression(prefixes[_token]);
            break;
          case '-':
            result = -parseExpression(prefixes[_token]);
            break;
          default:
            if(isalpha(_token))
            {
              string variable;
            
              while(isalnum(_token))
              {
                variable += ShortToString(_token);
                _nextToken();
              }
              
              if(_token == '(')
              {
                const string name = variable;
                const int index = _functionTable.index(name);
                if(index == -1)
                {
                  error("Function undefined: " + name, __FUNCTION__);
                  return NULL;
                }
                
                const int arity = _functionTable[index].arity();
                if(arity > 0 && _lookAhead() == ')')
                {
                  error("Missing arguments for " + name + ", " + (string)arity + " required!", __FUNCTION__);
                  return NULL;
                }
                
                Promise *params[];
                ArrayResize(params, arity);
                for(int i = 0; i < arity; i++)
                {
                  params[i] = parseExpression(infixes[',']);
                  if(i < arity - 1)
                  {
                    if(_token != ',')
                    {
                      _match(',', ", expected (param-list)!", __FUNCTION__);
                      break;
                    }
                  }
                }
              
                _match(')', ") expected after " + (string)arity + " arguments!", __FUNCTION__);
                
                result = helper._call(index, params);
              }
              else
              {
                return helper._variable(variable); // 获取索引（如果找不到）- 选择使用 nan 保留名称
              }
            }
            else // 暗示数字，必须为数字 
            {
              string number;
              if(_readNumber(number))
              {
                return helper._literal(number);
              }
            }
        }
        return result;
      }

标识符后跟括号“(”，解释为函数调用。 我们为其解析时还创建了一个参数列表（根据函数 Arity），并用逗号分隔。 调用 parseExpression，根据逗号 “,” 优先级获取每个参数。 该函数的 Promise 对象是利用 helper._call() 生成的。 如果括号后没有标识符，则会为 helper._variable() 变量创建 Promise 对象。

当第一个标记不是字母时，_parsePrefix 方法尝试调用 _readNumber 读取数字，并调用 helper._literal() 为其创建 Promise。

_parseInfix 方法期望当前令牌是允许的中缀之一。 甚至，在第一个参数中，它接收已被读入 Promise *left 对象的左侧操作数。 第二个参数指定所要解析令牌的最小优先级。 一旦遇到优先级较低的内容，该子表达式即被视为结束。 _parseInfix 的目的是采用 'precedence' 调用 parseExpression，以便读取正确的操作数，然后，我们可以为二元操作相应的中缀创建 Promise 对象。

      Promise *_parseInfix(Promise *left, const int precedence = 0)
      {
        Promise *result = NULL;
        const ushort _previous = _token;
        switch(_previous)
        {
          case '*':
          case '/':
          case '%':
          case '+':
          case '-':
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '>':
          case '<':
            if(_lookAhead() == '=')
            {
              _nextToken();
              result = new Promise((uchar)(_previous == '<' ? '{' : '}'), left, parseExpression(precedence));
            }
            else
            {
              result = new Promise((uchar)_previous, left, parseExpression(precedence));
            }
            break;
          case '=':
          case '!':
            _matchNext('=', "= expected after " + ShortToString(_previous), __FUNCTION__);
            result = helper._isEqual(left, parseExpression(precedence), _previous == '=');
            break;
          case '&':
          case '|':
            _matchNext(_previous, ShortToString(_previous) + " expected after " + ShortToString(_previous), __FUNCTION__);
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '?':
            {
              Promise *truly = parseExpression(infixes[':']);
              if(_token != ':')
              {
                _match(':', ": expected", __FUNCTION__);
              }
              else
              {
                Promise *falsy = parseExpression(infixes[':']);
                if(truly != NULL && falsy != NULL)
                {
                  result = helper._ternary(left, truly, falsy);
                }
              }
            }
          case ':':
          case ',': // 跳过
            break;
          default:
            error("Can't process infix token " + ShortToString(_previous));
          
        }
        return result;
      }

重要的是，必须在 _previous 变量中记住方法开头的当前中缀令牌。 这样做是因为，若在成功的情况下，parseExpression 调用会将字符串中的位置移至其他令牌，即右移任意数量的符号。

我们只研究了 3 个方法，每个方法都拥有相当透明的结构，这便是普拉特解析器的整体。

其应用类似于 ExpressionCompiler 解析器：创建 ExpressionPratt 对象，设置变量表，启动表达式字符串的 “evaluate” 方法，并调用 resolve() 计算所接收 Promise 内的语法树。

当然，利用语法树并不是惰性评估的唯一方法。 下一款我们将要研究的解析器类型会运行在没有语法树的情况下，且其将评估算法写入所谓的字节码当中。 因此，我们先看看字节码是如何工作的。

字节码生成

字节码是一系列命令，以“快速”二进制表现形式描述整个计算算法。 字节码的创建类似于实际的编译。 但是，结果不包含处理器指令，而是包含控制某个计算器类的应用语言变量或结构。 在我们的例子中，执行单元是以下字节码结构：

  struct ByteCode
  {
      uchar code;
      double value;
      int index;
  
      ByteCode(): code(0), value(0.0), index(-1) {}
      ByteCode(const uchar c): code(c), value(0.0), index(-1) {}
      ByteCode(const double d): code('n'), value(d), index(-1) {}
      ByteCode(const uchar c, const int i): code(c), value(0.0), index(i) {}
      
      string toString() const
      {
        return StringFormat("%s %f %d", CharToString(code), value, index);
      }
  };

它的字段重复 Promise 对象的字段 — 不是全部，而是仅重复其中的一些，它们表示流计算所需的最小集合。 计算之所以繁琐，是因为命令会从左到右依次读取和执行，而无需在层次结构之间进行切换。

“code” 字段包含命令的本质（该值对应于 Promise 代码），“value” 字段包含一个数字（常量），而 “index” 字段包含在变量/函数表中的索引。

编写计算指令的方法之一是反向波兰语表示法，也称为后缀表示法。 这种表示法的思路是，运算符后随其操作数。 例如，通常的后缀符号 “a + b” 变为后缀 “a b +”，而更复杂的情况 “a + b * sqrt(c)” 变为 “a b c 'sqrt' * +”。

RPN 非常适合字节码，因为它能用堆栈轻松实现计算。 当程序在输入流中“看到”数字或变量引用时，它会把该值压入堆栈。 如果在输入流中遇到运算符或函数，则程序会从堆栈中弹出所需数量的值，用这些值执行指定的操作，然后将结果压回堆栈之中。 在该过程结束时，表达式评估结果会是堆栈上保留得唯一数字。

由于 RPN 为我们提供了构建相同表达式的语法树的替代方案，因此这两种表示形式可以相互转换。 我们来尝试基于 Promise 树生成一个字节码。 为了这样做，将 exportToByteCode 方法添加到 Promise 类中。

  class Promise
  {
    ...
    public:
      void exportToByteCode(ByteCode &codes[])
      {
        if(left) left.exportToByteCode(codes);
        const int truly = ArraySize(codes);
        
        if(code == '?')
        {
          ArrayResize(codes, truly + 1);
          codes[truly].code = code;
        }
        
        if(right) right.exportToByteCode(codes);
        const int falsy = ArraySize(codes);
        if(last) last.exportToByteCode(codes);
        const int n = ArraySize(codes);
        
        if(code != '?')
        {
          ArrayResize(codes, n + 1);
          codes[n].code = code;
          codes[n].value = value;
          codes[n].index = index;
        }
        else // (code == '?')
        {
          codes[truly].index = falsy; // 跳过 true 分支
          codes[truly].value = n;     // 跳过两个分支
        }
      }
      ...
  };

该方法接收一个字节码结构数组作为参数，它应该保存当前 Promise 对象的内容。 首先，它分析所有的从属节点，如果存在非零值，则递归调用该方法的 'left'，'right' 和 'last' 指针。 在此之后，当保存了所有操作数之后，Promise 对象的属性将写入字节码。

由于表达式的语法含有条件运算符，因此该方法还可以记住字节码数组在 true 和 false 指令分支开始处，以及条件表达式结尾处的大小。 这允许将条件数组中的偏移量写入条件运算符字节码结构，如果条件为真或假，则在计算过程中应跳过转该偏移量。 条件为真的指令分支在字节码 “?” 之后立即开始。 指令执行完毕后，我们应该根据 “value” 字段的偏移量跳转。 错误条件的指令分支则按 “index” 字段中的偏移量开始，紧接着是 “true” 指令字段中的偏移量。

请注意，当我们以解释或语法树模式评估表达式时，在二选一之前，会依据条件计算条件运算符的全部两个分支，这意味着计算分支其一毫无意义。 在字节码中，我们跳过不必要的分支计算。

为了将整个表达式语法树转换为字节码，需要针对 “evaluate” 返回的根对象调用 exportToByteCode。 这是普拉特解析器的示例：

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
  
    for(int i = 0; i < ArraySize(codes); i++)
    {
      Print(i, "] ", codes[i].toString());
    }

现在，我们需要编写函数，基于字节码执行计算。 我们将其添加到同一 Promise 类中，因为字节码会用到变量和函数索引，且 Promise 默认情况下含有指向这些表的链接。

  #define STACK_SIZE 100
  
  // 堆栈模仿
  #define push(S,V,N) S[N++] = V
  #define pop(S,N) S[--N]
  #define top(S,N) S[N-1]
  
  class Promise
  {
    ...
    public:
      static double execute(const ByteCode &codes[], VariableTable *vt = NULL, FunctionTable *ft = NULL)
      {
        if(vt) variableTable = vt;
        if(ft) functionTable = ft;
  
        double stack[]; int ssize = 0; ArrayResize(stack, STACK_SIZE);
        int jumps[]; int jsize = 0; ArrayResize(jumps, STACK_SIZE / 2);
        const int n = ArraySize(codes);
        for(int i = 0; i < n; i++)
        {
          if(jsize && top(jumps, jsize) == i)
          {
            --jsize; // 快速 "弹 & 压 （pop & drop）"
            i = pop(jumps, jsize);
            continue;

          }
          switch(codes[i].code)
          {
            case 'n': push(stack, codes[i].value, ssize); break;
            case 'v': push(stack, variableTable[codes[i].index], ssize); break;
            case 'f':
              {
                IFunctor *ptr = functionTable[codes[i].index];
                double params[]; ArrayResize(params, ptr.arity()); int psize = 0;
                for(int j = 0; j < ptr.arity(); j++)
                {
                  push(params, pop(stack, ssize), psize);
                }
                ArrayReverse(params);
                push(stack, ptr.execute(params), ssize);
              }
              break;
            case '+': push(stack, pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '-': push(stack, -pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '*': push(stack, pop(stack, ssize) * pop(stack, ssize), ssize); break;
            case '/': push(stack, Promise::safeDivide(1, pop(stack, ssize)) * pop(stack, ssize), ssize); break;
            case '%':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, fmod(first, second), ssize);
              }
              break;
            case '!': push(stack, (double)(!pop(stack, ssize)), ssize); break;
            case '~': push(stack, (double)(-pop(stack, ssize)), ssize); break;
            case '<':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first < second), ssize);
              }
              break;
            case '>':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first > second), ssize);
              }
              break;
            case '{':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first <= second), ssize);
              }
              break;
            case '}':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first >= second), ssize);
              }
              break;
            case '&': push(stack, (double)(pop(stack, ssize) && pop(stack, ssize)), ssize); break;
            case '|':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first || second), ssize); // 顺序很重要
              }
              break;
            case '`': push(stack, _precision < fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '=': push(stack, _precision > fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '?':
              {
                const double first = pop(stack, ssize);
                if(first) // true
                {
                  push(jumps, (int)codes[i].value, jsize); // 直至结束所在
                  push(jumps, codes[i].index, jsize);      // 我们从真实的终点跳跃
                }
                else // false
                {
                  i = codes[i].index - 1; // 由于即将出现 ++，因此需要 -1
                }
              }
              break;
            default:
              Print("Unknown byte code ", CharToString(codes[i].code));
          }
        }
        return pop(stack, ssize);
      }
      ...
  };

堆栈操控通过 'stack' 数组上的宏来实现，其中预先分配了一定数量 STACK_SIZE 的元素。 在压入和弹出操作期间，避免调用 ArrayResize 来加快执行速度。 STACK_SIZE 等于 100 看似对于大多数实际的单行表达式来说足够了。 否则我们就会遇到堆栈溢出。

为了控制可嵌套条件运算符的执行，我们需要使用额外的“跳转”堆栈。

从上面的 Promise 和普拉特解析器代码中我们已经熟悉了所有这些操作。 唯一的区别是堆栈作为操作数源，和存储中间结果的地方被广泛运用。 字节码在一个循环中执行，在单一方法中调用，没有递归。

此功能令我们能够从普拉特解析器或 ExpressionCompiler 导出语法树，并依据转换接收的字节码来计算表达式。

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
    double r = Promise::execute(codes);

稍后，在测试所有解析器时，我们将比较树形和字节码在计算时的性能速度。

但是引入字节码的主要目的是实现另一种解析器类型，“分流场”解析器。

分流场解析器 (ExpressionShuntingYard)

分流场解析器名称源于一种方法，该方法将输入令牌流切分成可立即传递到输出的令牌流，并应当推送到一个特殊堆栈上，从中可由有关令牌优先权组合的特殊规则提取令牌（堆栈中的令牌和输入流中的下一个令牌）。 解析器将输入表达式转换回 RPN（反向波兰表示法）。 对于我们来说这样很方便，因为我们可以立即生成字节码，无需语法树。 从一般描述中可以看出，分流方法是基于运算符的优先级的，这便是为什么这个解析器与普拉特解析器相关。 因此，它将作为 ExpressionPrecedence 子类实现。

这个解析器属于自下而上的类别。

一般来说，算法如下（我们此处省略了我们还不曾拥有的右关联性细节，以及与三元条件运算符相关的复杂性）：

  在循环中读取表达式的下一个标记（直到表达式结束）
    如果令牌是一元操作，则将其保存在堆栈中
    如果是一个数字，则将其写入字节码
    如果是一个变量，则将其索引写入字节码
    如果它是一个函数标识符，则将其索引保存在堆栈上
    如果令牌是中缀运算符
      只要 “(” 不在堆栈顶部，且堆栈顶部的运算符优先级 >= 当前运算符优先级，或函数位于顶部
        将堆栈顶部推入输出字节码
      将运算符保存到堆栈上
    如果令牌是 “(”，则将其保存在堆栈中
    如果令牌是 ')'
      只要堆栈顶不是 '('
        将堆栈顶部推入输出字节码
      如果堆栈顶是 '('，删除并废弃
  如果堆栈上还有遗留标记，则按顺序将它们移动到输出字节码中

显然，这个解析器的实现只需要一个方法。

整个 ExpressionShuntingYard 类如下所示。 主体公开方法 convertToByteCode 开始解析，执行则在 exportToByteCode 当中。 由于我们的表达式支持条件运算符，所以递归调用 exportToByteCode 来解析它们的子表达式。

  class ExpressionShuntingYard: public ExpressionPrecedence
  {
    public:
      ExpressionShuntingYard(const string vars = NULL): ExpressionPrecedence(vars) { }
      ExpressionShuntingYard(VariableTable &vt): ExpressionPrecedence(vt) { }
  
      bool convertToByteCode(const string expression, ByteCode &codes[])
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          exportToByteCode(codes);
        }
        return !_failed;
      }
  
    protected:
      template<typename T>
      static void _push(T &stack[], T &value)
      {
        const int n = ArraySize(stack);
        ArrayResize(stack, n + 1, STACK_SIZE);
        stack[n] = value;
      }
  
      void exportToByteCode(ByteCode &output[])
      {
        ByteCode stack[];
        int ssize = 0;
        string number;
        uchar c;
        
        ArrayResize(stack, STACK_SIZE);
        
        const int previous = ArraySize(output);
        
        while(_nextToken() && !_failed)
        {
          if(_token == '+' || _token == '-' || _token == '!')
          {
            if(_token == '-')
            {
              _push(output, ByteCode(-1.0));
              push(stack, ByteCode('*'), ssize);
            }
            else if(_token == '!')
            {
              push(stack, ByteCode('!'), ssize);
            }
            continue;
          }
          
          number = "";
          if(_readNumber(number)) // 如果读取了一个数字，则 _token 已更改
          {
            _push(output, ByteCode(StringToDouble(number)));
          }
          
          if(isalpha(_token))
          {
            string variable;
            while(isalnum(_token))
            {
              variable += ShortToString(_token);
              _nextToken();
            }
            if(_token == '(')
            {
              push(stack, ByteCode('f', _functionTable.index(variable)), ssize);
            }
            else // 变量名
            {
              int index = -1;
              if(CheckPointer(_variableTable) != POINTER_INVALID)
              {
                index = _variableTable.index(variable);
                if(index == -1)
                {
                  if(_variableTable.adhocAllocation())
                  {
                    index = _variableTable.add(variable, nan);
                    _push(output, ByteCode('v', index));
                    error("Unknown variable is NaN: " + variable, __FUNCTION__, true);
                  }
                  else
                  {
                    error("Unknown variable : " + variable, __FUNCTION__);
                  }
                }
                else
                {
                  _push(output, ByteCode('v', index));
                }
              }
            }
          }
          
          if(infixes[_token] > 0) // 运算符，包括最低有效值 '?'
          {
            while(ssize > 0 && isTop2Pop(top(stack, ssize).code))
            {
              _push(output, pop(stack, ssize));
            }
            
            if(_token == '?' || _token == ':')
            {
              if(_token == '?')
              {
                const int start = ArraySize(output);
                _push(output, ByteCode((uchar)_token));
                exportToByteCode(output); // 子表达式为真，_token 已经改变了
                if(_token != ':')
                {
                  error("Colon expected, given: " + ShortToString(_token), __FUNCTION__);
                  break;
                }
                output[start].index = ArraySize(output);
                exportToByteCode(output); // 子表达式为假，_token 已经改变了
                output[start].value = ArraySize(output);
                if(_token == ':')
                {
                  break;
                }
              }
              else
              {
                break;
              }
            }
            else
            {
              if(_token == '>' || _token == '<')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '<' ? '{' : '}')), ssize);
                  _nextToken();
                }
                else
                {
                  push(stack, ByteCode((uchar)_token), ssize);
                }
              }
              else if(_token == '=' || _token == '!')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '!' ? '`' : '=')), ssize);
                  _nextToken();
                }
              }
              else if(_token == '&' || _token == '|')
              {
                _matchNext(_token, ShortToString(_token) + " expected after " + ShortToString(_token), __FUNCTION__);
                push(stack, ByteCode((uchar)_token), ssize);
              }
              else if(_token != ',')
              {
                push(stack, ByteCode((uchar)_token), ssize);
              }
            }
          }
          
          if(_token == '(')
          {
            push(stack, ByteCode('('), ssize);
          }
          else if(_token == ')')
          {
            while(ssize > 0 && (c = top(stack, ssize).code) != '(')
            {
              _push(output, pop(stack, ssize));
            }
            if(c == '(') // 除非是子表达式，否则必须为 true（那么 “c” 可以为 0）
            {
              ByteCode disable_warning = pop(stack, ssize);
            }
            else
            {
              if(previous == 0)
              {
                error("Closing parenthesis is missing", __FUNCTION__);
              }
              return;
            }
          }
        }
        
        while(ssize > 0)
        {
          _push(output, pop(stack, ssize));
        }
      }
      
      bool isTop2Pop(const uchar c)
      {
        return (c == 'f' || infixes[c] >= infixes[_token]) && c != '(' && c != ':';
      }
  };

分流场解析器的用法不同于以前的类型。 我们在此跳过调用 “evaluate” 接收语法树的步骤。 取而代之，convertToByteCode 方法立即返回所传递表达式的字节码。

  ExpressionShuntingYard sh;
  sh.variableTable().adhocAllocation(true);
  
  ByteCode codes[];
  bool success = sh.convertToByteCode("x + y", codes);
  if(success)
  {
    sh.variableTable().assign("x=10;y=20");
    double r = Promise::execute(codes);
  }

不同类型的解析器的概览至此完毕。 类示意图如下所示：

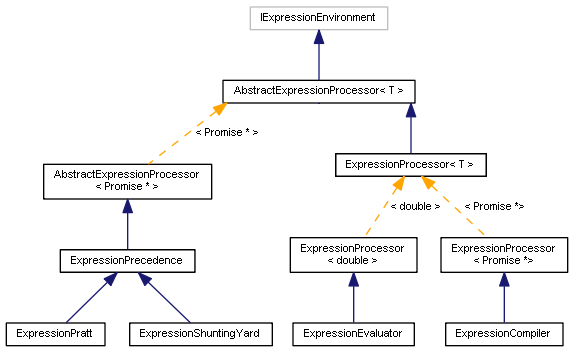
解析器类示意图

为了测试和比较不同的解析器，我们稍后将创建一个测试脚本。

鉴于最终的应用领域是交易，我们来看看如何用技术指标来扩展标准函数列表。

在表达式中嵌入指标作为函数

在计算表达式时，交易者也许需要一些特殊的信息，如余额、持仓数量、指标读数、等等。 通过扩展函数列表，所有这些都可在表达式当使用。 为了展示这种方法，我们将移动平均指标添加到函数集合之中。

将指标嵌入表达式的机制基于前面所研究的函子，由此，可从 AbstractFunc 类派生来实现。 正如我们已知，所有 AbstractFunc 族类实例都会自动注册到 AbstractFunctStorage 当中，并在函数表中可用。

  class IndicatorFunc: public AbstractFunc
  {
    public:
      IndicatorFunc(const string n, const int a = 1): AbstractFunc(n, a)
      {
        // 单参数是柱线数量，
        // 两个参数是柱线数量和缓冲区索引
      }
      static IndicatorFunc *create(const string name);
  };

Metatrader 5 中指标的具体特点是，它们还需要两个应用阶段：首先我们需要创建指标（为了获取其描述），然后从中请求数据。 在表达式处理的上下文中，第一步应该在解析期间执行，第二步应该在求值期间执行。 由于创建指标时需要指定所有参数，因此它们必须以名称实现，取代通过函数参数中传递。 例如，如果我们采用参数（period，method，price_type）创建 “iMA” 函数，那么在解析阶段我们只会收到它的名称，而参数的定义会推迟到执行阶段，这时创建指标已经太晚了（因为我们在这个阶段应该从指标中读取数据）。

作为解决方案，我们可以为移动平均指标保留一组名称。 名称按照以下规则组成：method_price_period。 此处，'method' 是 ENUM_MA_METHOD 枚举里有意义的单词之一 (SMA, EMA, SMMA, LWMA); 'price' 是 ENUM_APPLIED_PRICE 枚举中的价格类型之一 (CLOSE, OPEN, HIGH, LOW, MEDIAN, TYPICAL, WEIGHTED); 'period' 是一个整数。 因此，运用 “SMA_OPEN_10” 函数应基于开盘价创建一个简单移动平均线，周期为 10。

指标函数参数个数默认等于 1。 唯一的参数用于传递柱线数量。 如果参数个数设置为 2，则第二个参数表示缓冲区数量。 移动平均线不需要它。

MAIndicatorFunc 类依据参数所需的相应名称创建指标实例。

  class MAIndicatorFunc: public IndicatorFunc
  {
    protected:
      const int handle;
      
    public:
      MAIndicatorFunc(const string n, const int h): IndicatorFunc(n), handle(h) {}
      
      ~MAIndicatorFunc()
      {
        IndicatorRelease(handle);
      }
      
      static MAIndicatorFunc *create(const string name) // SMA_OPEN_10(0)
      {
        string parts[];
        if(StringSplit(name, '_', parts) != 3) return NULL;
        
        ENUM_MA_METHOD m = -1;
        ENUM_APPLIED_PRICE t = -1;
        
        static string methods[] = {"SMA", "EMA", "SMMA", "LWMA"};
        for(int i = 0; i < ArraySize(methods); i++)
        {
          if(parts[0] == methods[i])
          {
            m = (ENUM_MA_METHOD)i;
            break;
          }
        }
  
        static string types[] = {"NULL", "CLOSE", "OPEN", "HIGH", "LOW", "MEDIAN", "TYPICAL", "WEIGHTED"};
        for(int i = 1; i < ArraySize(types); i++)
        {
          if(parts[1] == types[i])
          {
            t = (ENUM_APPLIED_PRICE)i;
            break;
          }
        }
        
        if(m == -1 || t == -1) return NULL;
        
        int h = iMA(_Symbol, _Period, (int)StringToInteger(parts[2]), 0, m, t);
        if(h == INVALID_HANDLE) return NULL;
        
        return new MAIndicatorFunc(name, h);
      }
      
      double execute(const double &params[]) override
      {
        const int bar = (int)params[0];
        double result[1] = {0};
        if(CopyBuffer(handle, 0, bar, 1, result) != 1)
        {
          Print("CopyBuffer error: ", GetLastError());
        }
        return result[0];
      }
  };

“create” 工厂方法解析传递给它的名称，从名称中提取参数，并使用 “handle” 创建一个指标。 指标值是通过标准函子方法获得 — execute。

由于将来可将其他指标添加到函数当中，IndicatorFunc 类为任何指标的请求提供一个单一的入口点，即 “create” 方法。 截至目前，它只包含一个转发 MAIndicatorFunc::create() 的调用：

  static IndicatorFunc *IndicatorFunc::create(const string name)
  {
    // TODO:支持更多指标类型，根据名称调度调用
    return MAIndicatorFunc::create(name);
  }

该方法必须从函数表调用，因此请将所需代码添加到 FunctionTable 类中。

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      ...
      #ifdef INDICATOR_FUNCTORS
      virtual int index(const string name) override
      {
        int i = _table.getIndex(name);
        if(i == -1)
        {
          i = _table.getSize();
          IFunctor *f = IndicatorFunc::create(name);
          if(f)
          {
            Table<IFunctor *>::add(name, f);
            return i;
          }
          return -1;
        }
        return i;
      }
      #endif
  };

如果在内置的 25 个函数列表中找不到传递来的名称，新版本的 “index” 方法将尝试查找合适的指标。 为了连接这个附加功能，我们需要定义 INDICATOR_FUNCTORS 宏。

启用此选项后，我们可以计算以下表达式："EMA_OPEN_10(0)/EMA_OPEN_21(0)"。

实际上，所调用指标的参数通常在设置中提供。 这意味着它们必须以某种方式动态插入到表达式行中。 为了简化此任务，AbstractExpressionProcessor 类支持一个特殊的表达式预处理选项。 为了简洁起见，本文省略了对它的阐述。 启用预处理由 “evaluate” 方法的第二个可选参数管理（默认情况下等于 false，即禁用预处理）。

该选项的操作如下。 在表达式中，我们可以用大括号指定一个变量名，在解析之前它会被替换为变量值。 例如，如果表达式等于 “EMA_TYPICAL_{Period}(0)”，若变量表包含 Period 变量且值为 11，那么将分析成 “EMA_TYPICAL_11(0)”。

为了测试指标函数，我们稍后将创建一个智能交易系统，根据评估的表达式生成交易信号，包括移动平均值。

但我们首先需要确保解析器能工作正常。

测试脚本（ExpressParser）

测试脚本 ExpresSParserS.mq5 包括一套功能测试，和 4 种解析器类型计算速度的测量，以及各种模式的演示，语法树和字节码的记录，把指标作为内置函数的运用。

功能测试包括正确的和故意设置错误的应用程序（未声明的变量、零除、等等）。 测试的正确性取决于实际结果与预期结果的一致性，这意味着错误也可以是“正确的”。 例如，此处是普拉特t解析器测试日志的样子。

  Running 19 tests on ExpressionPratt* …
  1 passed, ok: a > b ? b > c ? 1 : 2 : 3 = 3.0; expected = 3.0
  2 passed, ok: 2 > 3 ? 2 : 3 > 4 ? 3 : 4 = 4.0; expected = 4.0
  3 passed, ok: 4 > 3 ? 2 > 4 ? 2 : 4 : 3 = 4.0; expected = 4.0
  4 passed, ok: (a + b) * sqrt(c) = 8.944271909999159; expected = 8.944271909999159
  5 passed, ok: (b == c) > (a != 1.5) = 0.0; expected = 0.0
  6 passed, ok: (b == c) >= (a != 1.5) = 1.0; expected = 1.0
  7 passed, ok: (a > b) || sqrt(c) = 1.0; expected = 1.0
  8 passed, ok: (!1 != !(b - c/2)) = 1.0; expected = 1.0
  9 passed, ok: -1 * c == -sqrt(-c * -c) = 1.0; expected = 1.0
  10 passed, ok: pow(2, 5) % 5 = 2.0; expected = 2.0
  11 passed, ok: min(max(a,b),c) = 2.5; expected = 2.5
  12 passed, ok: atan(sin(0.5)/cos(0.5)) = 0.5; expected = 0.5
  13 passed, ok: .2 * .3 + .1 = 0.16; expected = 0.16
  14 passed, ok: (a == b) + (b == c) = 0.0; expected = 0.0
  15 passed, ok: -(a + b) * !!sqrt(c) = -4.0; expected = -4.0
  16 passed, ok: sin ( max ( 2 * 1.5, 3 ) / 3 * 3.14159265359 ) = -2.068231111547469e-13; expected = 0.0
  lookUpVariable error: Variable is undefined: _1c @ 7: 1 / _1c^
  17 passed, er: 1 / _1c = nan; expected = nan
  safeDivide error: Error : Division by 0! @ 15: 1 / (2 * b - c)^
  18 passed, er: 1 / (2 * b - c) = inf; expected = inf
  19 passed, ok: sqrt(b-c) = -nan(ind); expected = -nan(ind)
  19 tests passed of 19
  17 for correct expressions, 2 for invalid expressions

如您所见，所有 19 个测试都成功完成。 在两次测试中，我们收到了预期的错误。

仅在一个多次计算的循环中进行了速度测量。 当以解释器运行时，这包括了表达式解析阶段，因为它每次计算后都要马上执行。 对于所有其他解析器类型，解析阶段是在“外部”完成。 对于所有方法，表达式解析一次性花费的时间大致相等。 这是测量 10000 次循环的结果之一（微秒）。

  >>> Performance tests (timing per method)
  Evaluation: 104572
  Compilation: 25011
  Pratt bytecode: 23738
  Pratt: 24967
  ShuntingYard: 23147

正如预期的那样，表达式预先“编译”的计算速度比解释型速度快若干倍。 我们还可以得出结论，最快的计算是基于字节码的计算。 在这种情况下，获取字节码的方法没有实质性的区别，因此我们即可以使用普拉特解析器，或或分流场方法。 您可以根据您的个人参考，以及您对算法的理解程度来选择解析器，或者选择最适合您特定任务的解析器，例如语法扩展，或与现有程序的集成。

使用表达式来为智能交易系统设置信号（ExprBot）

表达式为交易机器人生成交易信号。 与简单地更改参数相比，这样做提供了更大的灵活性。 由于函数的可扩展列表，它提供了与 MQL 几乎相同的功能，然而在此它不需要编译。 此外，常规操作可以很容易地隐藏在现成的函子中。 这在产品设置灵活性和复杂性之间提供了平衡性。

我们已拥有了一套移动平均指标，因此我们的交易系统将以这些指标为基础（尽管，我们可以在表达式中添加时间函数、风险管理、即时报价和其他数据）。

为了演示这个原理，我们来创建一个简单的智能系统 ExprBot。 变量 SignalBuy 和 SignalSell 将包含执行买卖交易的条件表达式。 以下公式可在两个基于均线交叉的策略里运用。

  #define INDICATOR_FUNCTORS
  #include <ExpresSParserS/ExpressionCompiler.mqh>
  
  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
  input string Variables = "Threshold=0.01";
  input int Fast = 10;
  input int Slow = 21;

阈值设置为常数，仅是为了演示随机变量的输入。 快速和慢速平均周期的参数在解析表达式之前应将其插入表达式，作为指标名称的一部分。

由于有两个信号，我们实例化了两个递归下降解析器。 一般来讲，我们只使用一个，但两个表达式中的变量表可能存在潜在差异，在这种情况下，我们需要在每次计算之前切换上下文。

  ExpressionCompiler ecb(Variables), ecs(Variables);
  Promise *p1, *p2;

在 OnInit 处理程序中，将参数保存在变量表中，并构建语法树。

  int OnInit()
  {
    ecb.variableTable().set("Fast", Fast);
    ecb.variableTable().set("Slow", Slow);
    p1 = ecb.evaluate(SignalBuy, true);
    if(!ecb.success())
    {
      Print("Syntax error in Buy signal:");
      p1.print();
      return INIT_FAILED;
    }
    ecs.variableTable().set("Fast", Fast);
    ecs.variableTable().set("Slow", Slow);
    p2 = ecs.evaluate(SignalSell, true);
    if(!ecs.success())
    {
      Print("Syntax error in Sell signal:");
      p2.print();
      return INIT_FAILED;
    }
    
    return INIT_SUCCEEDED;
  }

整个策略在 OnTick 处理程序中编写（这里省略了辅助函数；还需要包括 MT4Orders 函数库）。

  #define _Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
  #define _Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)
  
  void OnTick()
  {
    if(!isNewBar()) return;
    
    bool buy = p1.resolve();
    bool sell = p2.resolve();
    
    if(buy && sell)
    {
      buy = false;
      sell = false;
    }
    
    if(buy)
    {
      OrdersCloseAll(_Symbol, OP_SELL);
      if(OrdersTotalByType(_Symbol, OP_BUY) == 0)
      {
        OrderSend(_Symbol, OP_BUY, Lot, _Ask, 100, 0, 0);
      }
    }
    else if(sell)
    {
      OrdersCloseAll(_Symbol, OP_BUY);
      if(OrdersTotalByType(_Symbol, OP_SELL) == 0)
      {
        OrderSend(_Symbol, OP_SELL, Lot, _Bid, 100, 0, 0);
      }
    }
    else
    {
      OrdersCloseAll();
    }
  }

这两个表达式由 “promises” p1 和 p2 计算。 结果则是，我们有两个标志“买入”和“卖出”，它们在相应的方向上开仓或平仓。 MQL 代码保证一次只能有一笔持仓，因此，如果信号相反（如果您用了更复杂的表达式，或错误地设置了负阈值，则可能发生这种情况），则任何现有持仓都将平仓。 可以在解析器函数中以不同的方式编辑信号条件。

如果在策略测试器中启动 EA，结果很可能不是很好。 然而，重要的是，交易现由解析器管理。 它们未提供现成的盈利系统，但提供了寻找策略的额外工具。

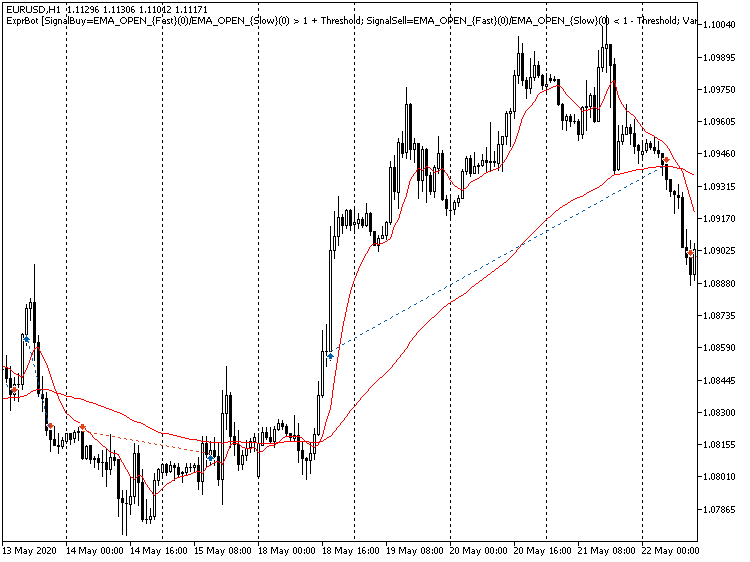
利用表达式计算信号进行交易的示例

结束语

在这两篇文章中，我们研究了四种解析器类型，比较了它们的功能，以及可以嵌入到 MQL 程序中的实现类。 所有解析器使用相同的语法，最常用的数学运算，和 25 个函数。 如有必要，可以通过扩展支持的运算符列表、添加新的内置应用程序函数（指标、价格、贸易统计数据）和语法结构（特别是用于处理它们的数组和函数）来扩展语法。

该技术能够更灵活地将设置和不可变的 MQL 代码隔离。 对于最终用户来说，通过编辑输入参数中的表达式来定制算法的能力似乎更容易，且无需学习 MQL 编程的基础知识；而这些基础知识在查找所需代码片段、按照规则编辑代码片段，和处理潜在编译错误所必需的。 从 MQL 程序开发人员的角度来看，表达式解析和评估支持还提供了其他优势，例如，它可以转换为“在 MQL 之上的脚本”的潜在能力，这能够避免函数库和 MQL 编译器的版本控制。