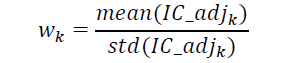前言
东方证券研报《动态情景多因子Alpha模型》指出,由于不同股票之间的基本面情况是有差异的,同一只股票在不同时间的基本面也可能不同,对所有股票一视同仁地打分评价,忽视了个股之间的基本面情况差异和选股因子在不同风格股票池里的适用性。
进一步,如果以行业或市值作为划分依据进行打分,从一定程度上弥补了全市场打分的缺陷,然而这样的方法也存在一定的问题:
首先,行业分类一般是根据公司收入的来源,而公司收入来源相似不能代表公司的基本面一致。例如对于技术类公司,成熟的公司和高速成长的公司收入来源相同,但基本面可能完全不同,高速成长的技术类公司完全有可能和高速增长的其他类型公司基本面更相似。
其次,对行业进行单独建模时,同一行业内的股票数量相对有限,统计检验得到的有效因子可能是对历史数据噪音的过度拟合,从而真实效果无法得到确定。
为了解决上述问题,同时能够捕捉股票之间的差异性,建立了动态情景模型(Dynamic Contextual Alpha Model)。DCA概念由Sorenson,Hua and Qian(2005)首先提出,它摒弃了行业内打分的做法,转而根据股票基本面属性把股票分层,对每个层内的股票单独打分,最后得到每个股票的综合得分。本文借鉴这个模型,针对A股市场进行调整,即将A股市场所有股票按照不同情景进行划分,如规模、价值、成长、盈利能力、技术等。然后在不同的股票类型中配置最优因子权重。
一、选择情景分层因子,进行初步检验。
在动态情景模型的构建中,首先应该考虑的是如何选择分层因子。分层的目标是把具有相似基本面的股票收集到一起,不同情景的分层应该能够刻画股票基本面上不同的属性。我们希望不同的因子在不同的分层后效果会有显著差异。因此要从不同情景类型中选出对市场风格切换有较强捕捉能力且本身相对稳定的因子,具体来说我们希望分层因子有如下特征:
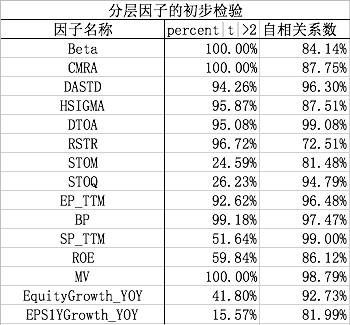
1、 因子的IC正负显著比例之和(percent |t| >2)较高。
2、 因子横截面间的线性自相关系数较高,自身稳定。
3、 不同分层因子之间的因子值的横截面秩相关系数较低,能够在不同维度较为独立地刻画股票特征。
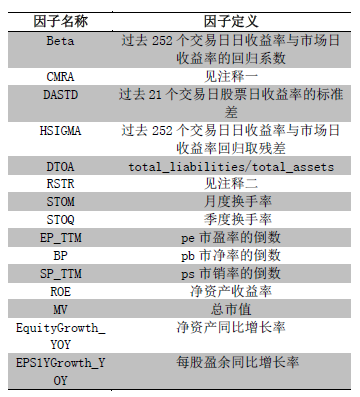
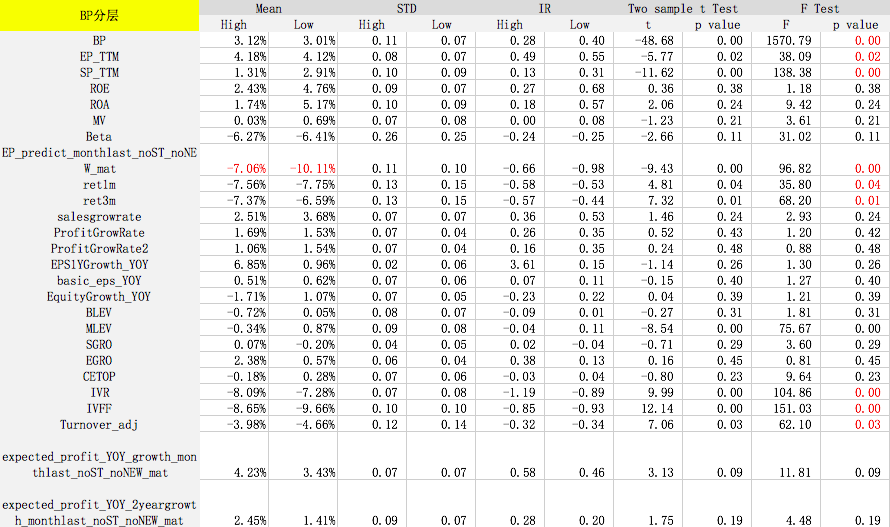
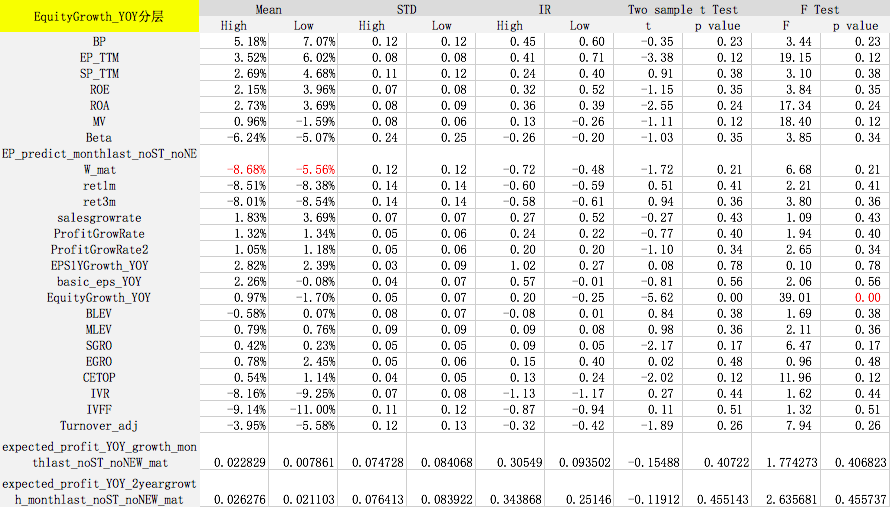
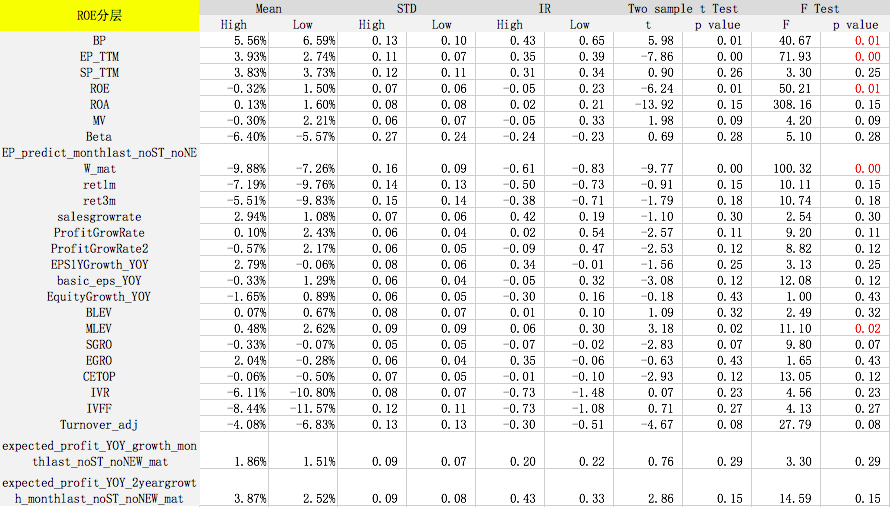
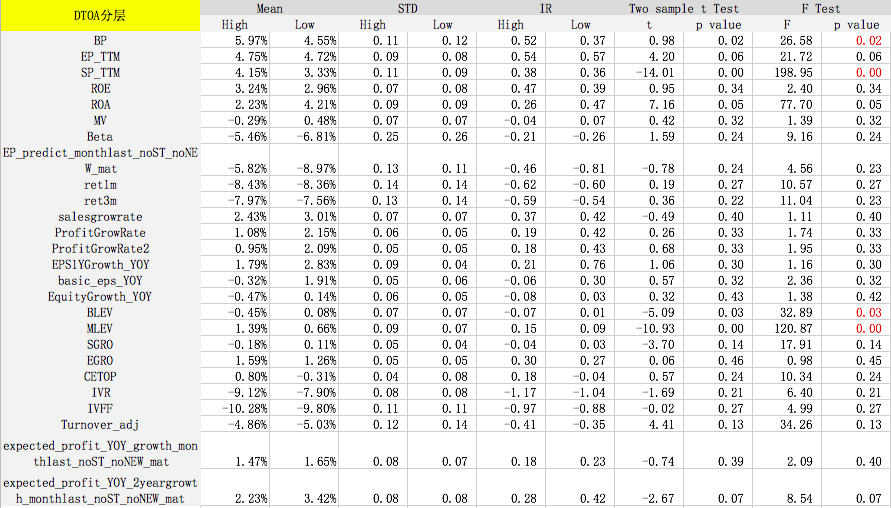
我们从不同情景中分别选择了几个定义简单、逻辑明确、样本覆盖率较高的因子作为分层因子的备选因子,并进行初步检验,结果如下图所示:
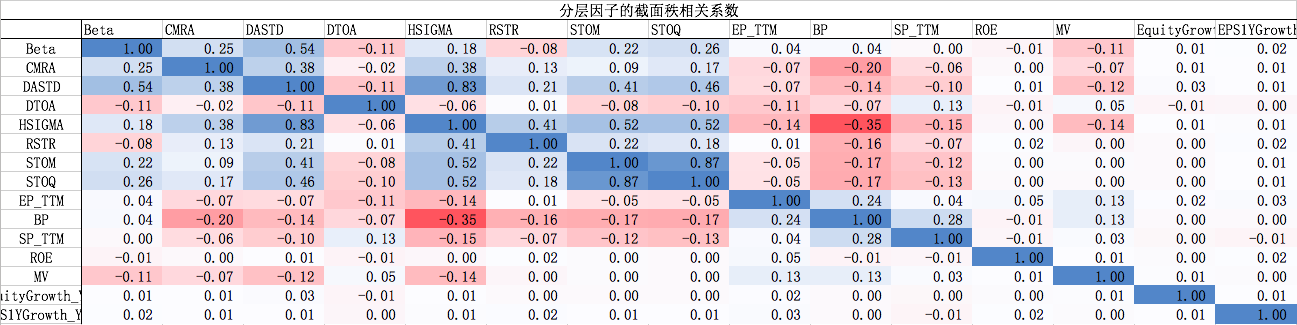
下面计算备选分层因子间的横截面秩相关系数,再对时间序列求平均值,得到的结果如下表所示。秩相关系数高说明不同因子对样本空间的划分趋于一致,实际上并没有在新的情景维度对股票分层。
至此,我们通过上述的因子初步检验,选定了八个不同维度的情景分层因子,分别是:规模因子MV、价值因子BP、成长因子EquityGrowth_YOY、盈利因子ROE、残差波动率因子CMRA、杠杆因子DTOA、技术类因子RSTR、流动性因子STOQ。
二、因子在不同维度分层下的测试。
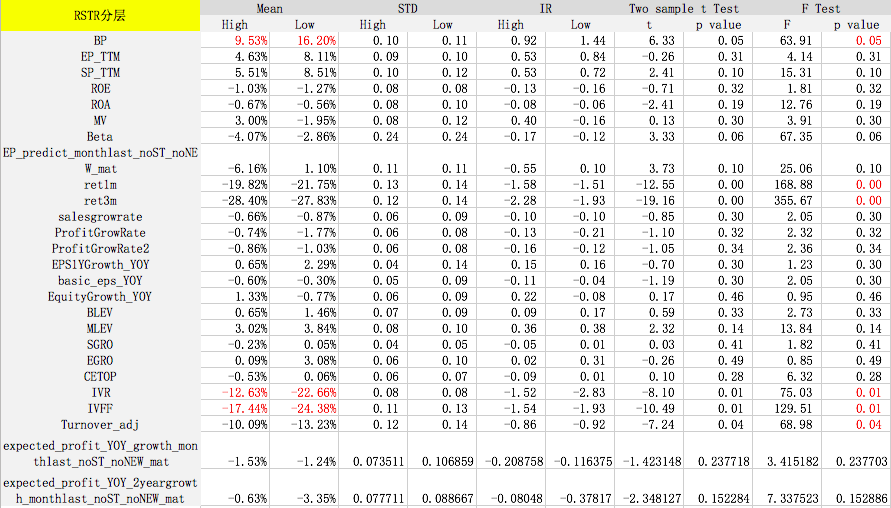
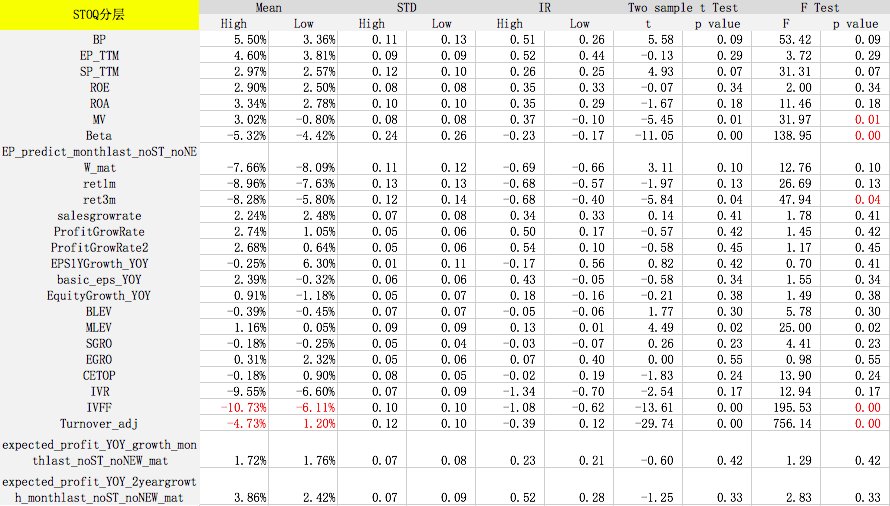
选出情景分层因子后,我们在各分层因子的不同维度下测试其他因子的IC和IR,利用t和F统计检验众多因子在不同分层下IC均值、IC标准差是否有显著的差别。
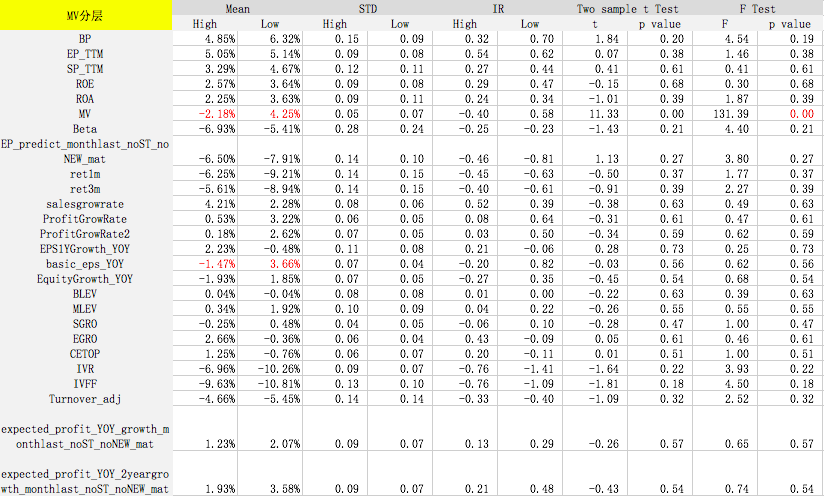
测试时间为2007年10月到2017年10月,检验样本空间为所有股票。每个月初按照分层因子将全样本空间等分为股票数量相同的两部分(High和Low),如大市值和小市值。然后计算其他因子分别在这两个样本空间的风险调整后IC和IR。风险调整后的IC计算方式如下:
ICadj=corr(fpure,rresidual)ICadj=corr(fpure,rresidual)
IC{adj}=corr(f{pure},r{residual})fpure=f?b1X?b2log(mktcap)fpure=f?b1X?b2log?(mktcap)
f{pure}=f-b1X-b_2log?(mktcap)rresidual=r?m1X?m2log(mktcap)rresidual=r?m1X?m2log?(mktcap)
r{residual}=r-m_1X-m_2log?(mktcap)其中X是行业虚拟变量矩阵,log(mktcap)是总市值的对数,f是前一个月月初的原始因子值,r是当月个股的收益率。在每个月初进行OLS横截面回归,得到风险调整后的因子值和收益率,进而通过计算相关系数得到每个月初所有股票的风险调整IC。风险调整IC可以减弱行业和市值的影响,更准确地反应因子本身的预测能力。
F Test的p值小于等于0.05表示拒绝原假设(原假设为因子在分层前后收益没有显著差异),即该因子在不同的分层中表现是不一样的。可以看出,对于某些因子在某些分层下,预测能力出现显著差异,因此针对基本面不同的股票,我们可以采取不同的评价体系。
三、构建个股情景特征向量。
前面只是简单地通过分层因子将所有股票分为两部分,而在实际操作中,属于同一分层的股票的特征也不尽相同,为了对个股在不同情景分层上的属性进行更准确的定量刻画,下面我们构建个股的情景特征向量。
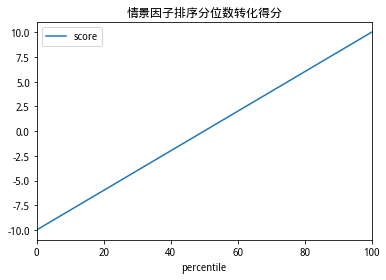
首先计算个股的因子值在当月月初全体股票中所处的分位数(0%~100%),定义得分score,以此来描述股票的情景相似度。下图为分数和score的对应关系。
score=(percentile(Si)?50)/5score=(percentile(Si)?50)/5
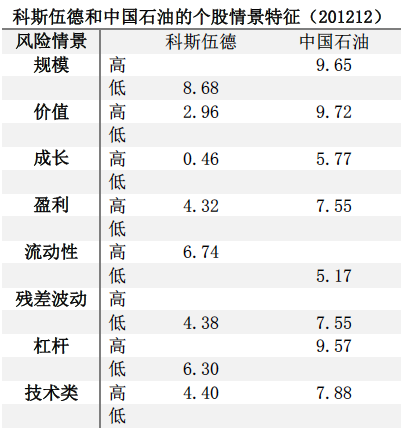
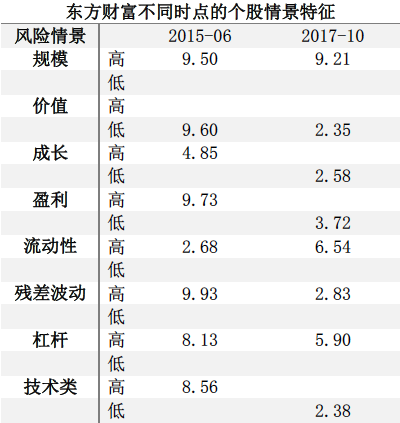
score=(percentile(S_i )-50)/5我们根据股票在每个情景因子上的得分情况,就能对每只股票建立特征向量,如下表所示。此方法既可以用来比较同一时间不同股票的基本面差异,也可以用来比较同一只股票不同时间点的基本面变化。
如下表所示,在2012年12月,创业板股票科斯伍德的规模显著小于蓝筹股中国石油,在低规模特征上得分较高;此外由于创业板小盘股交投更加活跃,因此科斯伍德在高流动性上得分显著高于中国石油在流动性情景的得分。
下表显示从2015年6月到2017年10月,东方财富(300059.XSHE)的情景特征向量变化,可以看出在这段时间内,东方财富的规模得分变化较小,价值、流动性得分有所升高,而成长、残差波动、杠杆这三个情景的得分有所下降,盈利能力和技术维度的得分发生了显著下降。特征向量的变化也可以说明某段时间内该股票在各维度的能力是上升还是下降。
四、情景模型的因子加权矩阵。
根据上述结果,发现在不同情景分层中,个别因子的预测能力存在显著差异,因此我们尝试在不同的情景分层中给同一个因子赋予不同的权重,以期获得更加准确的预测结果。本文采用因子过去12个月的风险调整IC均值与标准差的比值作为确定因子权重的依据:
根据我们之前的众多因子研究及偏好,选择了如下的因子对股票进行打分:BP、EP_TTM、SP_TTM、IVFF、Turnover_adj、ProfitGrowthRate、EquityGrowth_YOY。
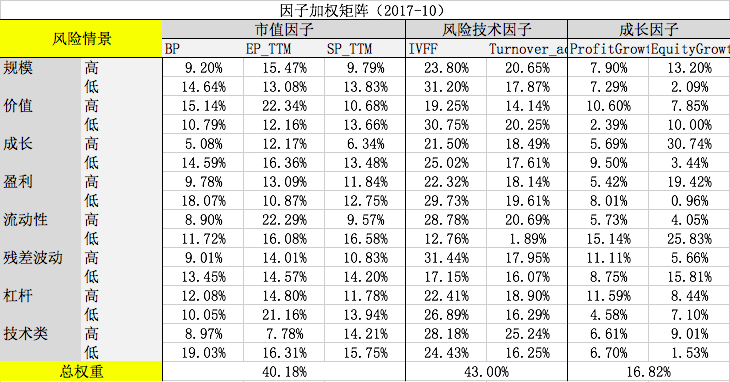
以2017年10月为例,因子加权矩阵如下图:
对于每个月份,我们都可以得到如上图所示的一个因子加权矩阵,这种加权方式有效地反应出了同样的因子在不同情景分层中的重要性,根据我们得到的权重,可以较传统的基本面研究方法更准确地判断股票基本面变化,以及提高因子的预测能力和预测稳定程度。
注释一:
该因子来自于Barra文档,具体计算方法如下:
注释二:
该因子来自于Barra文档,具体计算方法如下: