本篇內容用於研究組合優化方法對組合收益提升的影響,偏重於優化目標方法設置,標的選擇均是權益類資產,用於全A股測試,同時考慮到研究的實際意義,我們設置行業資產配置這樣的組合情境(同樣也可以做不同板塊配置優化),基於申萬一級行業數據,采用了較為常見的最小方差、最大夏普、風險平價這樣的模型,應用在行業配置中,來探索組合優化模型效果。
組合優化的目的在於給予高收益,低風險的標的更多的權重,來提高組合整體表現。策略里面大部分情況下都會默認平均持倉的方法,由於沒有考慮各個標的風險的不同,標的之間的相關性,並未較好的解決雞蛋在一個籃子里的問題,若是稍加關注一下對組合權重的處理,就會考慮到各標的間的漲跌是否本身就有較強關聯這樣的問題,這個時候就是需要研究各標的時間序列協方差、波動率等內容的時候。
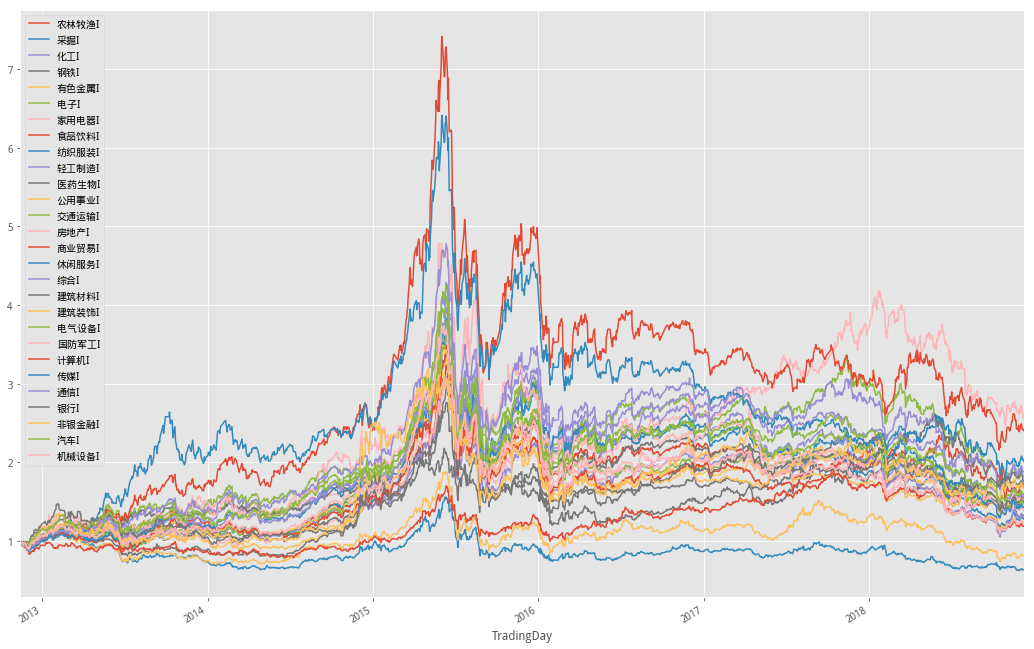
接下來將28個申萬一級行業指數進行研究,給予不同權重配置,首先,獲取了行業指數數據,構造收益序列效果如下圖所示
可以看到,各行業之間漲跌存在一定的差異
但在極端行情如2015年6月之前的牛市和之後的熊市都有着一致的表現
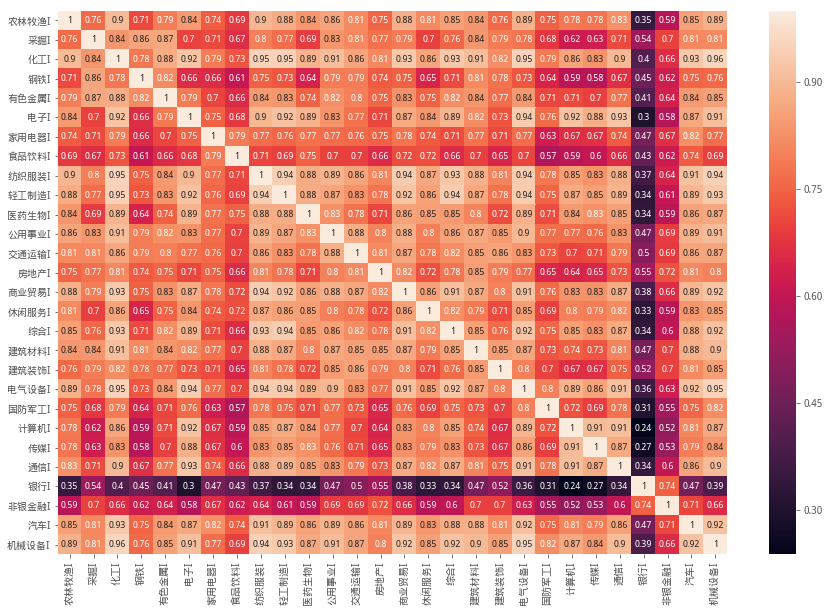
下面獲取了行業間相關矩陣,並以熱力圖進行展示
熱力圖顏色又深到淺表示相關度有低到高的過程
從圖中可以明顯看到銀行業與非銀金融與其他行業有着較為明顯的不同
化工、電器設備、機械設備、紡織服裝等行業都有較高的相關度
開始之前,我們先對這些優化方法進行說明
1)平均分倉
就是對28個行業進行等權重資金配置
2)等波動率
等波動率是使得每個股票貢獻的表征風險相等,如組合中第i個標的的權重為,波動率為
滿足如下條件:
即權重應滿足如下關系
此優化方法下的行業配置權重
3)最小方差
最小方差,也可以稱為最小波動或最低風險
為投資權重向量,為各標的的收益率協方差矩陣
組合的波動率滿足,即尋找使得最小的
此優化方法下的行業配置權重
4)風險平價
風險平價模型是通過衡量組合各標的對於組合的風險貢獻度,來制定投資模型的各類資產權重,目標是使得組合標的達到等風險貢獻
此優化方法下的行業配置權重
5)最大夏普
夏普率用來表示每承受一單位風險,會產生多少的超額報酬,是對策略的收益與風險進行綜合考慮
目標函數為追求最大
即尋找目標,使得目標最小
此優化方法下的行業配置權重
以下是不同組合優化的淨值表現
我們調用scipy.optimize提供的優化算法,構造以上的目標函數,進行優化求解。
模型模擬了季度調倉,保存調倉時點計算出的權重結構,構造回測,並計算相應風險指標,得出如下結果
研究結論
以下結論是基於對近5年申萬行業指數時間序列不同組合優化方法得出
(1)組合優化處理後普遍優於平均分倉的效果
(2)最小方差組合效果顯著,累計收益從39.2%提升至76.9%,年化收益從7.98%提升至12.85%,最大回撤從56.46%降低至40.51%,夏普比率從0.12提升至0.41
(3)最大夏普模型表現最差,且模型持股過於集中
(4)幾種優化方法整體提升效果一般,區分度不夠明顯,如年化波動0.2467略微降低至0.2187,最大回撤僅從56.46%優化到47.87%
組合優化方法是分散化投資的理論工具,分散化投資降低風險,是尋找相關度低的資產作為投資標的,而A股市場標的基本都有着較高的貝塔值,這使得所有行業同樣與大盤有着一致的牛熊,因此組合優化效果不盡如人意,基於組合優化方法,在更為宏觀的市場領域內,選擇相關度低的資產進行配置,這樣的場景能更好的發揮組合優化模型的工具優勢。
組合優化在行業配置中的應用?
研究目的?
本篇內容用於研究組合優化方法對組合收益提升的影響,偏重於優化目標方法設置,標的選擇均是權益類資產,用於全A股測試,同時考慮到研究的實際意義,我們設置行業資產配置這樣的組合情境(同樣也可以做不同板塊配置優化),基於申萬一級行業數據,采用了較為常見的最小方差、最大夏普、風險平價這樣的模型,應用在行業配置中,來探索組合優化模型效果。 下面是結果展示
研究內容?
組合優化的目的在於給予高收益,低風險的標的更多的權重,來提高組合整體表現。策略里面大部分情況下都會默認平均持倉的方法,由於沒有考慮各個標的風險的不同,標的之間的相關性,並未較好的解決雞蛋在一個籃子里的問題,若是稍加關注一下對組合權重的處理,就會考慮到各標的間的漲跌是否本身就有較強關聯這樣的問題,這個時候就是需要研究各標的時間序列協方差、波動率等內容的時候。
接下來我們將28個申萬一級行業指數進行研究,進行行業的不同權重配置,整個研究內容分布如下
- 第一部分:數據準備階段
- 通過聚寬平台數據獲取申萬一級行業指數行情
- 構造收益序列
- 相關性矩陣展示行業關聯信息
- 第二部分:構造組合目標函數
- 獲取調倉日曆信息
- 構造組合優化方法
- 計算並記錄調倉權重
- 第三部分:回測收益檢查
- 進行回測收益統計
- 風險指標匯總
研究結論?
以下結論是基於對近5年申萬行業指數時間序列的不同組合優化方法得出
(1)組合優化處理後普遍優於平均分倉的效果
(2)最小方差組合效果顯著,累計收益從39.2%提升至76.9%,年化收益從7.98%提升至12.85%,最大回撤從56.46%降低至40.51%,夏普比率從0.12提升至0.41
(3)最大夏普模型表現最差,且模型持股過於集中
(4)幾種優化方法整體提升效果一般,區分度不夠明顯,如年化波動0.2467略微降低至0.2187,最大回撤僅從56.46%優化到47.87%
組合優化方法是分散化投資的理論工具,分散化投資降低風險,是尋找相關度低的資產作為投資標的,而A股市場標的基本都有着較高的貝塔值,這使得所有行業同樣與大盤有着一致的牛熊,因此組合優化效果不盡如人意,基於組合優化方法,在更為宏觀的市場領域內,選擇相關度低的資產進行配置,這樣的場景能更好的發揮組合優化模型的工具優勢。
第一部分 數據準備?
#導入需要的庫
import pandas as pd
import numpy as np
from jqdata import jy
from jqdata import *
import seaborn as sns
import matplotlib as mpl
from cvxopt import solvers, matrix
import datetime as dt
from scipy.optimize import minimize
我們通過聚寬獲取申萬行業指數
為了統計近5年的行業配置組合優化效果,且考慮到需要一年的協方差數據,這里獲取6年的行業指數準備數據
#獲取所需的數據
s_date,e_date = '2012-11-10','2018-12-10'
moneyfund_price = get_price('511880.XSHG',start_date=s_date,end_date=e_date)
#通過聚源數據獲取申萬行業指數行情數據(輸入行業指數代碼)
def get_SW_index(SW_index = 801010,start_date = '2017-01-31',end_date = '2018-01-31'):
index_list = ['PrevClosePrice','OpenPrice','HighPrice','LowPrice','ClosePrice','TurnoverVolume','TurnoverValue','TurnoverDeals','ChangePCT','UpdateTime']
jydf = jy.run_query(query(jy.SecuMain).filter(jy.SecuMain.SecuCode==str(SW_index)))
link=jydf[jydf.SecuCode==str(SW_index)]
rows=jydf[jydf.SecuCode==str(SW_index)].index.tolist()
result=link['InnerCode'][rows]
df = jy.run_query(query(jy.QT_SYWGIndexQuote).filter(jy.QT_SYWGIndexQuote.InnerCode==str(result[0]), jy.QT_SYWGIndexQuote.TradingDay>=start_date, jy.QT_SYWGIndexQuote.TradingDay<=end_date
))
df.index = df['TradingDay']
df = df[index_list]
return df
hy_df = get_industries(name='sw_l1')
hy_price_dict = {}
for hy in hy_df.index[:]:
hy_price =get_SW_index(SW_index = hy,start_date = s_date,end_date = e_date)
hy_price_dict[hy] = hy_price['ClosePrice']
all_price_df = pd.concat(hy_price_dict.values(),axis=1)
all_price_df.columns = hy_df.index
#all_price_df['moneyfund'] = moneyfund_price['close']
all_price_df.head(5)
繪制各行業指數時間序列走勢圖
mpl.pyplot.style.use('ggplot')
all_price_df.columns = list(hy_df['name'].values)#+['貨幣基金']
mpl.rcParams['font.family']='serif'
mpl.rcParams['axes.unicode_minus']=False # 處理負號
prices=all_price_df
(prices/prices.iloc[0]).plot(figsize=(18,12),grid='on')
pct_daily = prices.pct_change()
可以看到,各行業之間漲跌存在一定的差異
但在極端行情如2015年6月之前的牛市和之後的熊市都有着一致的表現
行業間相關性矩陣計算,並以熱力圖進行展示
#計算各行業指數相關矩陣
fig = plt.figure(figsize= (15,10))
ax = fig.add_subplot(111)
ax = sns.heatmap(pct_daily.corr(),annot=True,annot_kws={'size':9,'weight':'bold'})
熱力圖顏色又深到淺表示相關度有低到高的過程
從圖中可以明顯看到銀行業與非銀金融與其他行業有着較為明顯的不同
化工、電器設備、機械設備、紡織服裝等行業都有較高的相關度
第二部分 構造組合優化目標?
(1)按季度調倉日期獲取
我們設置季度調倉,進行組合風險平衡
#獲取日期列表
#按月、季度、半年方式獲取交易日列表
def get_tradeday_list(start,end,frequency=None,count=None):
if count != None:
df = get_price('000001.XSHG',end_date=end,count=count)
else:
df = get_price('000001.XSHG',start_date=start,end_date=end)
if frequency == None or frequency =='day':
return df.index
else:
df['year-month'] = [str(i)[0:7] for i in df.index]
if frequency == 'month':
return df.drop_duplicates('year-month').index
elif frequency == 'quarter':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='04') | (df['month']=='07') | (df['month']=='10') ]
return df.drop_duplicates('year-month').index
elif frequency =='halfyear':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='06')]
return df.drop_duplicates('year-month').index
get_tradeday_list(start=s_date,end=e_date,frequency="quarter",count=None)
獲取近5年按季度調倉日期
s_date,e_date = '2013-12-10','2018-12-10'
tradedays = get_tradeday_list(start=s_date,end=e_date,frequency="quarter",count=None)
tradedays
(2)優化目標說明
1)平均分倉
平均分倉就是對28個行業進行等權重資金配置
2)等波動率
等波動率是使得每個股票貢獻的表征風險相等,如組合中第i個標的的權重為$w_i$,波動率為$w_i\sigma_i$
滿足如下條件: $$ w_1\sigma_1 = w_2\sigma_2=...... =w_i\sigma_i$$
即權重應滿足如下關系$$1/\sigma_1:1/\sigma_2:......:1/\sigma_i$$
3)最小方差
最小方差,也可以稱為最小波動或最低風險
$w$為投資權重向量,$\Sigma$為各標的的收益率協方差矩陣
組合的波動率滿足$\sigma = \sqrt{w^T\Sigma w }$,只要找到$w$使得$w^T\Sigma w $最小即可
4)風險平價
風險平價模型是通過衡量組合各標的對於組合的風險貢獻度,來制定投資模型的各類資產權重。
風險平價的目標是均衡配置多個資產的風險,使得組合標的達到等風險貢獻
5)最大夏普
夏普率用來表示每承受一單位風險,會產生多少的超額報酬,是對策略的收益與風險進行綜合考慮。 $$SharpeRatio = {R_p-R_f\over\sigma_p}$$ $R_p 是策略年化收益, R_p = w_1r_1+w_2r_2+......+w_ir_i $
$R_f = 無風險利率(默認0.04)$
$\sigma_p 是策略收益波動率,\sigma_p = \sqrt{w^T\Sigma w }$
目標函數為 $$\smash{\displaystyle\max_{w}} {WR - R_f\over \sqrt{w^T\Sigma w}\sqrt{250}}$$
即尋找目標$w$,使得目標$(-1)*SharpeRatio$最小
接下來進行不同的優化目標,獲取權重並保存記錄
#計算調倉時權重配置並保存為字典
#記錄加入權重後的組合收益時間序列
t0=dt.datetime.now()
weights_dict = {}
returns_df = pd.DataFrame()
num = 1
ret_daily = pct_daily+1
weights_name = ['mean_weights','mean_vol','min_var','risk_parity','max_sharpe']
for date_temp1,date_temp2 in zip(tradedays[:-1],tradedays[1:]):
t1=dt.datetime.now()
#獲取指定日期一年前的交易日日期
def get_before_tradeday(date):
return get_price('000001.XSHG',end_date=date,count=252).index[0]
date_before = get_before_tradeday(date_temp1)
#最小方差
def fun1(x):
risk = np.dot(x.T,np.dot(cov_mat,x))
return risk
#最大夏普
def fun2(x):
r_b = 0.04
pct_mean = pct_temp.mean()
p_r = (1+np.dot(x,pct_mean))**250-1
p_sigma = np.sqrt(np.dot(x0.T,np.dot(cov_mat,x0))*250)
p_sharpe = (p_r-r_b)/p_sigma
return -p_sharpe
#風險平價
def fun3(x):
tmp = (omega * np.matrix(x).T).A1
risk = x * tmp/ np.sqrt(np.matrix(x) * omega * np.matrix(x).T).A1[0]
delta_risk = [sum((i - risk)**2) for i in risk]
return sum(delta_risk)
#計算協方差矩陣
pct_temp = pct_daily.loc[date_before:date_temp1,:]
cov_mat = pct_temp.cov()
omega = np.matrix(cov_mat.values)
#sicpy優化方法參數設置
x0 = np.ones(omega.shape[0]) / omega.shape[0]
bnds = tuple((0,None) for x in x0)
cons = ({'type':'eq', 'fun': lambda x: sum(x) - 1})
options={'disp':False, 'maxiter':1000, 'ftol':1e-20}
#平均分配權重
weights1 = np.array([1.0/pct_temp.shape[1]]*pct_temp.shape[1])
#等波動率
wts = 1/pct_temp.std()
weights2 = wts/wts.sum()
#模型求解組合方差最小時權重
weights3 = minimize(fun1,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
#風險平價
weights4 = minimize(fun3,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
#最大夏普
weights5 = minimize(fun2,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
weights_list = [weights1,weights2,weights3,weights4,weights5]
#統計收益
if num == 0:
returns1_df = pd.DataFrame()
for i in range(len(weights_list)):
weights_temp =[j if j > 0.0001 else 0.0 for j in weights_list[i]]
returns1_df[weights_name[i]] = (ret_daily.loc[date_temp1:date_temp2,:]*weights_temp).cumsum(axis=1).iloc[:,-1]
returns_df = pd.concat([returns_df,returns1_df],axis=0)
else:
#按權重的方式計算
for i in range(len(weights_list)):
weights_temp =[j if j > 0.0001 else 0.0 for j in weights_list[i]]
returns_df[weights_name[i]] = (ret_daily.loc[date_temp1:date_temp2,:]*weights_temp).cumsum(axis=1).iloc[:,-1]
num = 0
weights_dict[date_temp1] = weights_list
t2=dt.datetime.now()
print('計算到%s,已耗時%s秒'%(date_temp2,(t2-t1).seconds))
print('計算完畢,總耗時%s秒'%(t2-t0).seconds)
第三部分 回測收益檢查?
(1)不同組合優化方法下淨值表現
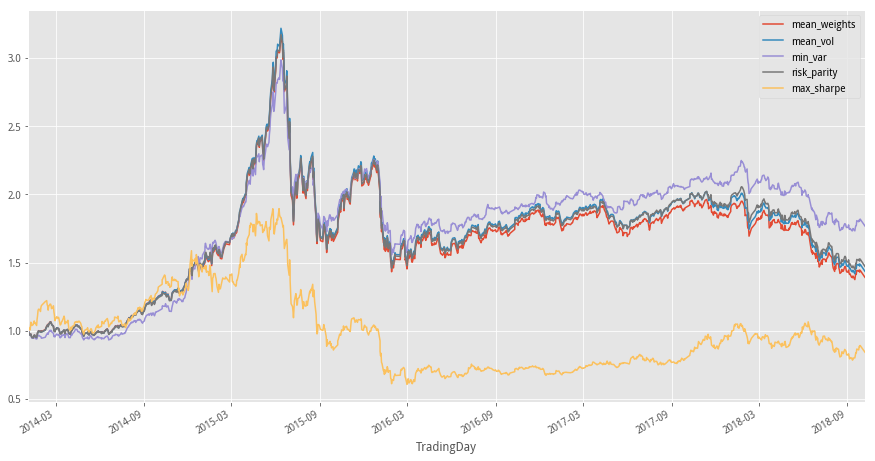
returns_df.cumprod(axis=0).plot(figsize=(15,8))
紅色的線是等權重配置,可以看到最小方差、風險平價、等波動率優化後是有增益效果
紫色的線是最波動最小,即最小方差配置,淨值表現最好
最大夏普和最小方差的是組合優化表現的兩個極端
中間三種組合方法的區分度不是很明顯,應該是行業間相關性過高的原因
mean_wts_df = pd.DataFrame()
meanvol_wts_df = pd.DataFrame()
minvar_wts_df = pd.DataFrame()
rp_wts_df = pd.DataFrame()
maxshp_wts_df = pd.DataFrame()
for date in weights_dict.keys():
#print(weights_dict[date][1])
mean_wts_df[date] = weights_dict[date][0]
meanvol_wts_df[date] = weights_dict[date][1]
minvar_wts_df[date] = weights_dict[date][2]
rp_wts_df[date] = weights_dict[date][3]
maxshp_wts_df[date] = weights_dict[date][4]
mean_wts_df = mean_wts_df.T
mean_wts_df.columns = list(hy_df['name'].values)
meanvol_wts_df = meanvol_wts_df.T
meanvol_wts_df.columns = list(hy_df['name'].values)
minvar_wts_df = minvar_wts_df.T
minvar_wts_df.columns = list(hy_df['name'].values)
rp_wts_df = rp_wts_df.T
rp_wts_df.columns = list(hy_df['name'].values)
maxshp_wts_df = maxshp_wts_df.T
maxshp_wts_df.columns = list(hy_df['name'].values)
下面對各種優化方法的權重配置進行展示
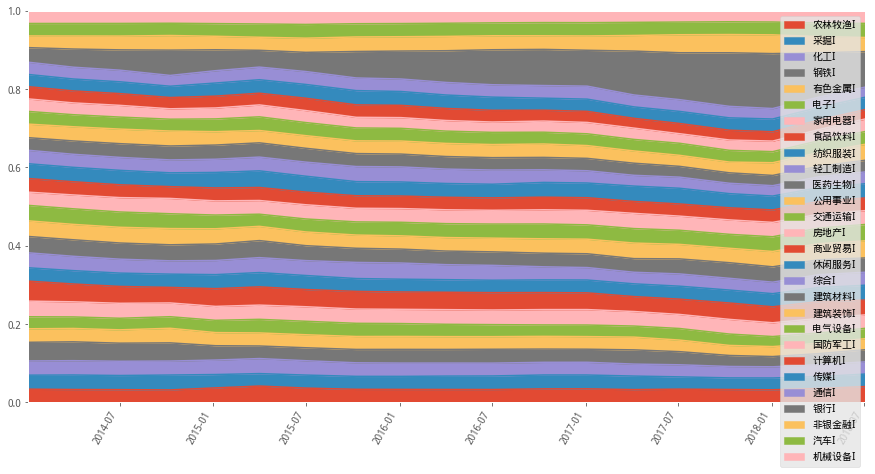
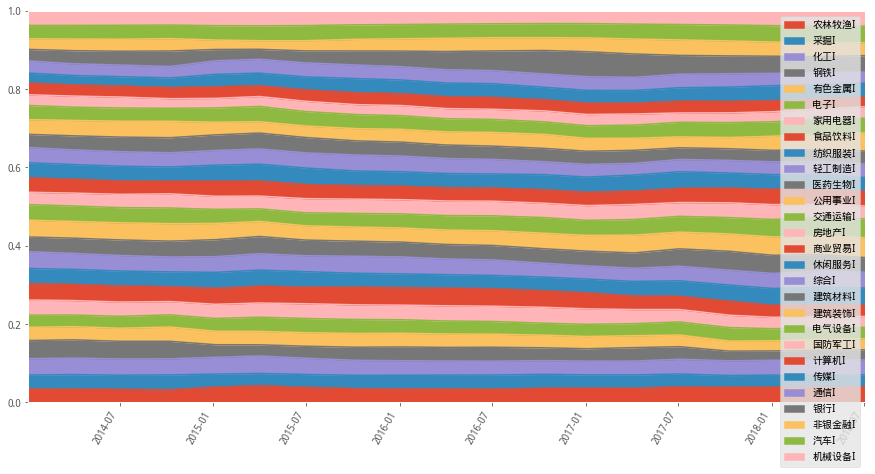
1)最小波動(最小方差)
#權重設置示意圖
minvar_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
組合長期對銀行有較高的權重配置,尤其在2015年熊市之後不斷進行權重增加,到2017年年初達到最大權重
下面我們貼一張同時期銀行指數走勢圖
可以看到銀行指數在2015年熊市之後逐步走強,尤其2016年到2017年的過程中漲幅明顯超過上證指數
注:(紅線為上證指數,紅綠相間為銀行指數行情)?
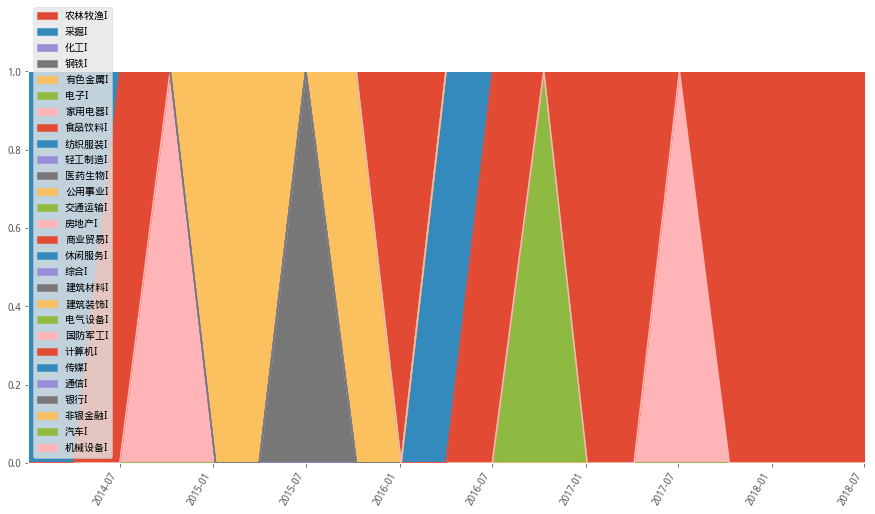
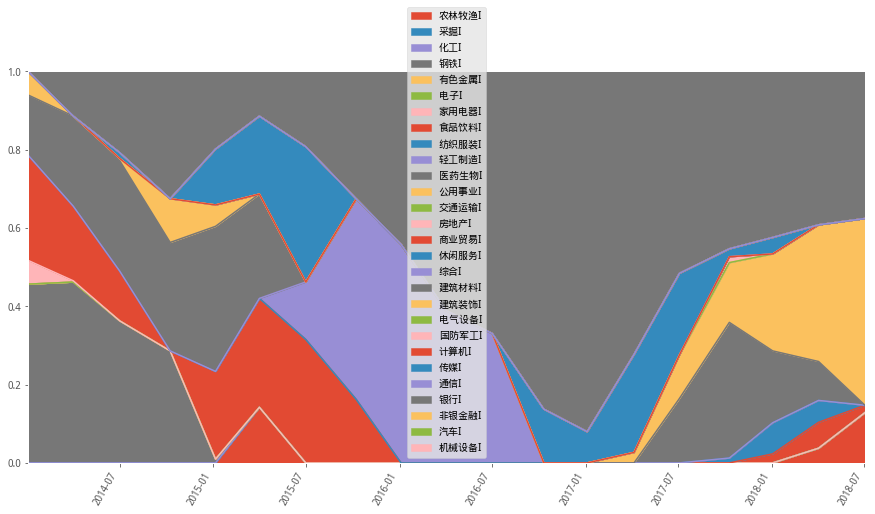
2)最大夏普
#權重設置示意圖
maxshp_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
從以上最大夏普和最小方差模型的配置權重中,可以看到有標的權重過於集中的情況
3)風險平價
#權重設置示意圖
rp_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
4)等波動率
#權重設置示意圖
meanvol_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
(2)收益風險指標匯總
#計算風險指標函數
def get_risk_index(pct_se):
return_se = pct_se.cumprod()-1
total_returns = return_se[-1]
total_an_returns = ((1+total_returns)**(250/len(return_se))-1)
vol = pct_se.std()*np.sqrt(250)
sharpe = (total_an_returns-0.04)/(np.std(pct_se)*250**0.5)
ret = return_se.dropna()
ret = ret+1
maxdown_list = []
for i in range(1,len(ret)):
low = min(ret[i:])
high = max(ret[0:i])
if high>low:
#print(high,low)
maxdown_list.append((high-low)/high)
#print((high-low)/high)
else:
maxdown_list.append(0)
max_drawdown = max(maxdown_list)
'''
print('策略收益:%s'%round(total_returns*100,2)+'%')
print('策略年化收益:%s'%round(total_an_returns*100,2)+'%')
print('夏普比率:%s'%round(sharpe,2))
print('最大回撤:%s'%round(max_drawdown*100,2)+'%')
print('年化波動率:%s'%round(vol,2))
'''
return total_returns,total_an_returns,sharpe,max_drawdown,vol
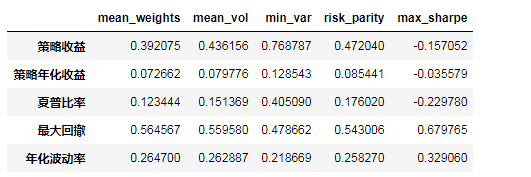
results=pd.DataFrame(index = ['策略收益','策略年化收益','夏普比率','最大回撤','年化波動率'])
for colu in returns_df.columns:
results[colu] = get_risk_index(returns_df[colu])
results
研究結論?
通過對本研究中基於近5年申萬行業指數時間序列的不同組合優化方法得出如下結論:
(1)進行組合優化處理後,均取得了優於平均分倉的效果
(2)最小方差組合效果顯著,累計收益從39.2%提升至76.9%,年化收益從7.98%提升至12.85%,最大回撤從56.46%降低至40.51%,夏普比率從0.12提升至0.41
(3)幾種優化方法整體提升效果一般,區分度不夠明顯,如年化波動0.2467略微降低至0.2187,最大回撤僅從56.46%優化到47.87%