何謂截面動量

在了解和測試了時間序列動量之後，我們自然想到按照經典策略分類的截面動量。時間序列動量很好理解，就是指單個商品自身是否發生上漲、下跌，以及其幅度是否構成我們應該買入多頭，賣出空頭這樣的操作。時間序列動量的假設是：某品種的價格產生方向會延續一定幅度，並且方向反轉也是個階段性過程，我們可以評估動量反轉而做出平倉或反手交易。

截面動量就不同了，它也被稱作是橫截面動量，在每個日期截面上，選擇上漲最多的N個品種做多，下跌最多的N個品種做空。它的假設是：強者恒強，弱者恒弱。動量是相對出現於品種之間的，而不是以一個絕對數值，體現出方向性。截面動量模型的持倉是對衝形態的，每一期賬戶內總有N個品種多頭，N個品種空頭。

我們查閱資料有顯示：Jegadeesh和Titman (1993)等人在對美國股市的研究開始了最早的金融市場中動量效應的研究，在排序期內考察各個股票的動量表現（即曆史業績），而在持有期開始時買入近期的勝者（業績較好），賣出近一期內的輸者（業績較差），並持有H的長度，直至下一個持有周期。之後Miffre和Rallis (2007)，Shen (2007) 以及Szakmary (2010)對國外商品期貨市場中的動量效應也做了測試，發現期貨市場中也確實存在着“勝者更強，輸者更弱”的現象。

截面動量的幾個關鍵問題

1、截面分組大小

首先需要討論的便是截面上不同品種的排名是否真的能夠區分開來，也就是說截面效應是否真的有效。為了查看分組對收益表現的影響，有機構研報里，通過截面動量從大到小的排名進行分組，標記排名前20%為做多組，後20%為做空組。

但是在期貨品種較少的年份，橫截面上品種數量不足20個的情況下，每次做多做空的品種可能只有3~4個左右，無法形成一個穩定的組合。所以我們在後期測試中，也嘗試了，前20%，前30%，前40%，這樣三組參數。

2、動量衡量和持有參數

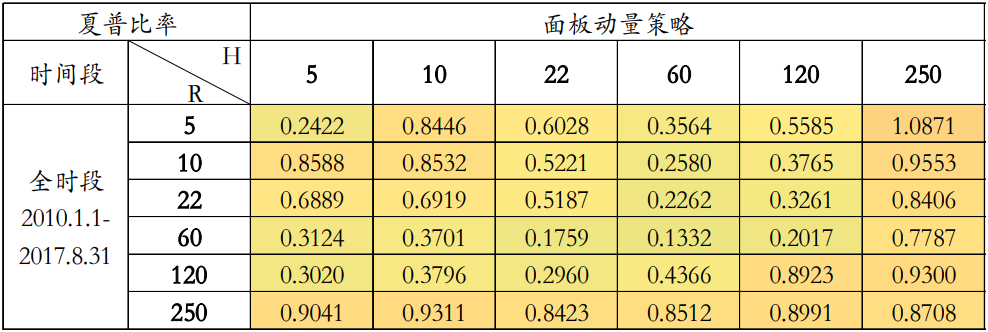
華泰期貨的測試顯示：橫截面動量策略涉及的參數主要有回溯期和持有期。回溯期指計算動量因子的時間長度，用 R 表示，代表建倉日前一天開始向前推 R 天，計算這 R 天的平均收益率；持有期指建倉後持有組合的時間長度，用 H 表示，代表每隔 H 天建倉，持有組合至下個建倉日。回溯期和持有期的取值範圍均是 5 天、10 天、22 天、60 天、120 天和 250 天，用（R，H）表示，共 36 個組合如下表所示。

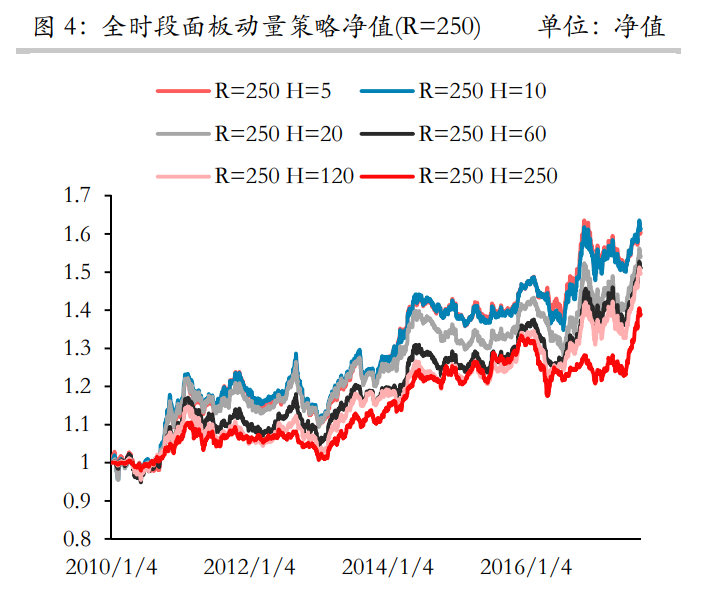
所以按照測試思路，華泰將動量的測試周期放在250日，在此周期下，測試了多個持有期的績效圖如下：

很可惜，我們不能認同250這個動量持有期。原因非常顯著：動量的計算僅考慮了開始和結束兩個時間端點，將近一年（250日）的考核期太過長久，這個策略變為一個典型的長線動量模型。試想，通過一年的考察期來評估各期貨品種動量，這個動量是難以發生變化和排序變化的，在調倉時間點可能不會產生調倉操作。所以實際測試中，我們更傾向於采用較為短期的動量考核期，構成一個相對容易解釋的策略。

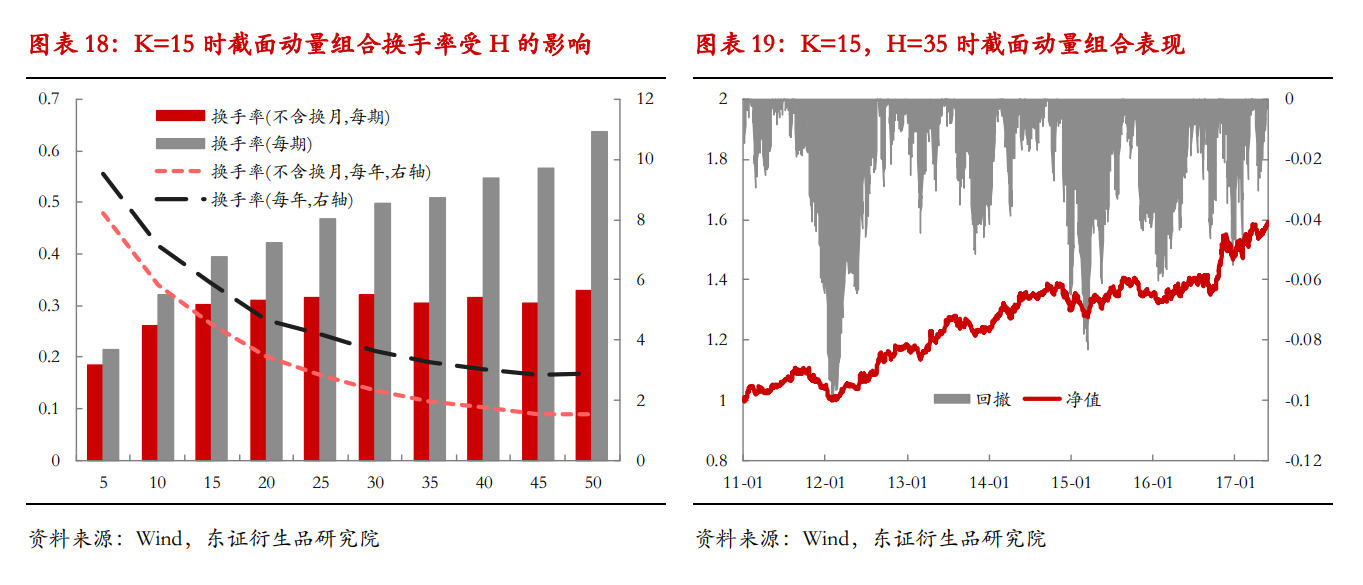
截面動量參數問題上，東方證券衍生品研究院的觀點是，截面動量因子的表現具有很強的參數敏感性。這是因為由不同的計算周期所得到動量特征表現結果不一，不同的品種的動量特征也會表現不一，所以在構建截面動量因子組合之後，組合的整體表現就會很強地受參數選擇的影響。

另外一個原因則和前文中提到的換手率的結論是一樣的，即持有期的長度取值較低時，交易次數會很多，由交易成本帶來的負面衝擊也較大。故綜合考慮之後，我們認為截面動量因子的有效性只存在部分參數區域內，較為合適的K值範圍為10天左右，而H的合理取值範圍為25天以上。

總之今天將這個框架公布出來，請大家自行確定動量的考察期和持有期參數。

代碼介紹

具體到寫碼環節，和之前講的價格模型類似，首先是初始化，我們給與的手續費還是挺高的，但是因為這是中低頻模型，對於手續費不敏感。

def initialize(context):
    # 設置參數
    set_parameter(context)
    # 設定基準銀華日利，在多品種的回測當中基準沒有參考意義
    set_benchmark('511880.XSHG')
    # 開啟動態複權模式(真實價格)
    set_option('use_real_price', True)
    # 過濾掉order系列API產生的比error級別低的log
    log.set_level('order', 'error')
    ### 期貨相關設定 ###
    # 設定賬戶為金融賬戶
    set_subportfolios([SubPortfolioConfig(cash=context.portfolio.starting_cash, type='futures')])
    # 期貨類每筆交易時的手續費是：買入時萬分之1,賣出時萬分之1,平今倉為萬分之1
    set_order_cost(OrderCost(open_commission=0.0001, close_commission=0.0001,close_today_commission=0.0001), type='index_futures')
    # 設定保證金比例
    set_option('futures_margin_rate', 0.15)
    # 設置滑點（單邊萬5，雙邊千1）
    set_slippage(PriceRelatedSlippage(0.001),type='future')
    # 開盤前運行
    run_daily( before_market_open, time='before_open', reference_security=get_future_code('RB'))
    # 開盤時運行
    run_weekly(market_open, 1,time='open', reference_security=get_future_code('RB'))
    # 交易運行 
    run_weekly(Trade, 1, time='open', reference_security=get_future_code('RB'))
    # 收盤後運行
    run_daily( after_market_close, time='after_close', reference_security=get_future_code('RB'))

在動量計算方面，代碼如下：
g.Momentum[ins]作為每個品種的代碼dict數據結構，可以看到它實際上是很簡單的一種動量計算方式。

## 開盤時運行函數
def market_open(context):
    # 輸出函數運行時間
    #log.info('函數運行時間(market_open):' str(context.current_dt.time()))
    # 以下是主循環
    for ins in g.instruments:
        # 過濾空主力合約品種
        if g.MappingReal[ins] != '':
            IndexFuture = g.MappingIndex[ins]
            RealFuture = g.MappingReal[ins]
            # 獲取當月合約交割日期
            end_date = get_CCFX_end_date(RealFuture)
            # 當月合約交割日當天不開倉
            if (context.current_dt.date() == end_date):
                return
            else:
                g.LastRealPrice[RealFuture] = attribute_history(RealFuture,1,'1d',['close'])['close'][-1]
                # 獲取價格list
                #if g.StatusTimer[ins] == 0:
                g.PriceArray[IndexFuture] = attribute_history(IndexFuture,g.BackWindow 5,'1d',['close','open','high','low'])

                # 如果沒有數據，返回
                if len(g.PriceArray[IndexFuture]) < 1:
                    return
                else: 
                    g.ClosePrice[ins] = g.PriceArray[IndexFuture]['close']
                    g.CurrentPrice[ins] = g.ClosePrice[ins][-1]
                    g.Price_DaysAgo[ins] = g.ClosePrice[ins][-g.BackWindow]

                    g.close = np.array(g.PriceArray[IndexFuture]['close'])
                    g.high = np.array(g.PriceArray[IndexFuture]['high'])
                    g.low = np.array(g.PriceArray[IndexFuture]['low'])
                    g.ATR[IndexFuture] = talib.ATR(g.high,g.low,g.close, g.BackWindow)[-1]

                    g.Momentum[ins] = g.CurrentPrice[ins]/g.Price_DaysAgo[ins] -1

動量的排序在這里：

## 交易模塊 
def Trade(context):
    # 定義每周買賣的列表
    log.info(g.ClosePrice.keys())
    BuyList = []
    SellList = []
    # 將字典進行排序，並將數值前五品種的symbol寫入列表
    a = sorted(g.Momentum.items(), key=lambda x: x[1],reverse = True)
    for i in range(int(g.Range*len(g.MappingReal.keys()))):
        BuyList.append(a[i][0])
        SellList.append(a[-i-1][0])

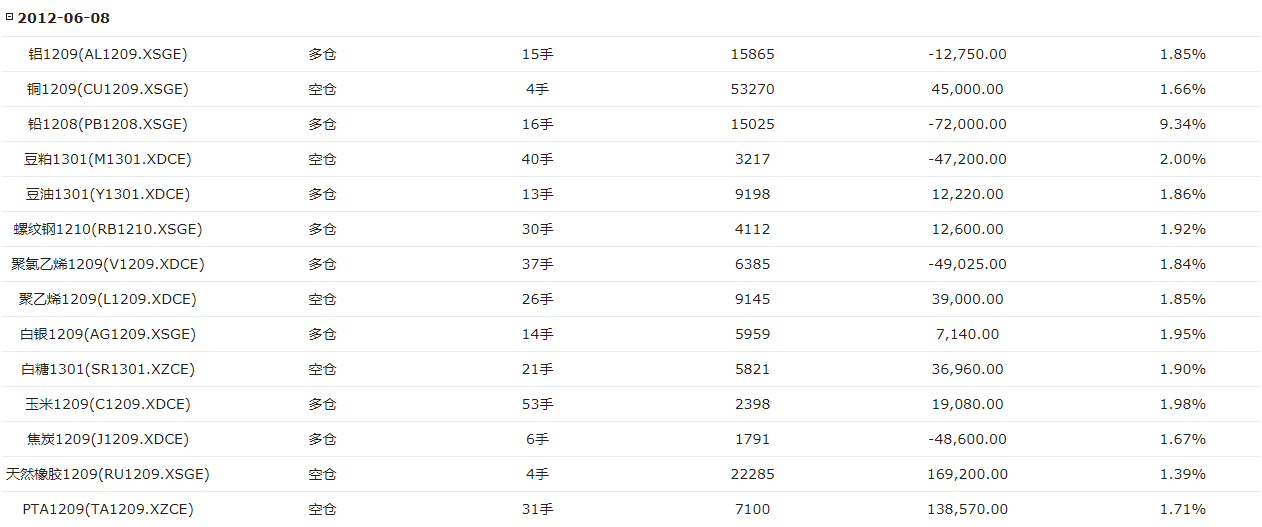
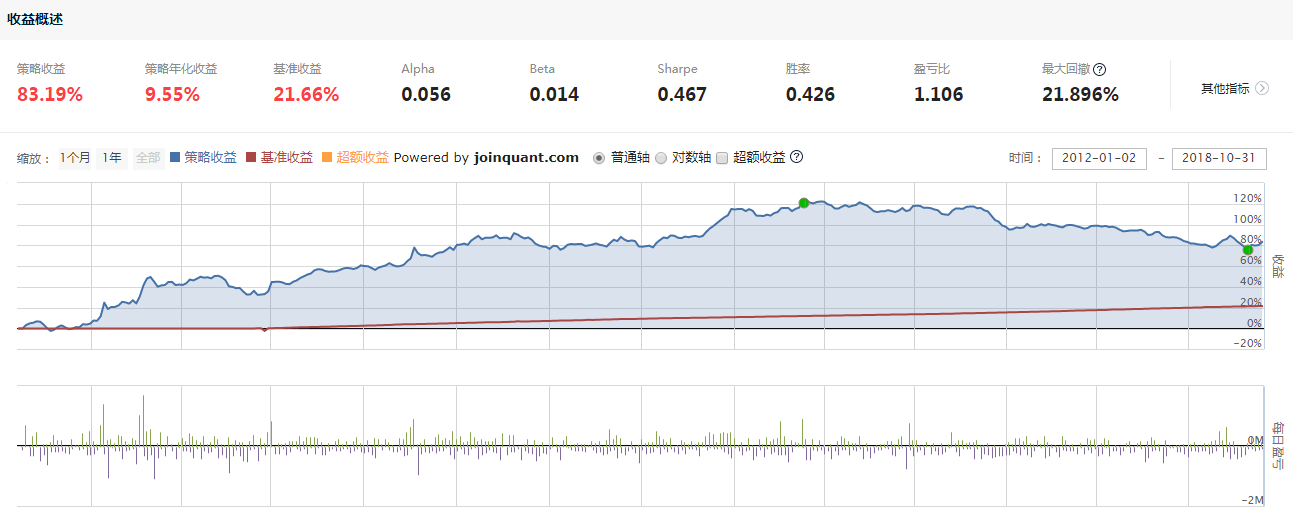
首先放上一個長期測試的績效圖如下，不知道這樣的績效你能否滿意，反正我覺得很難：

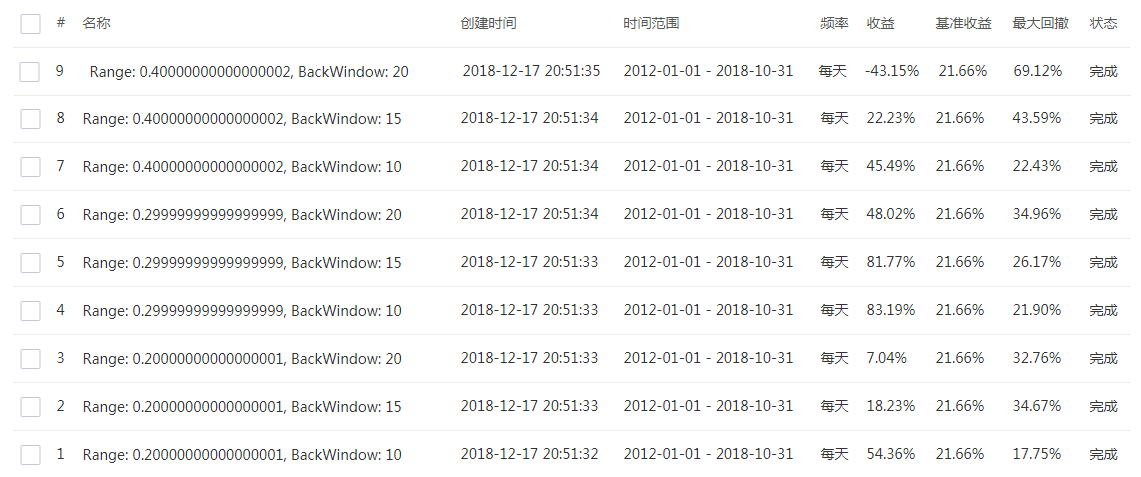
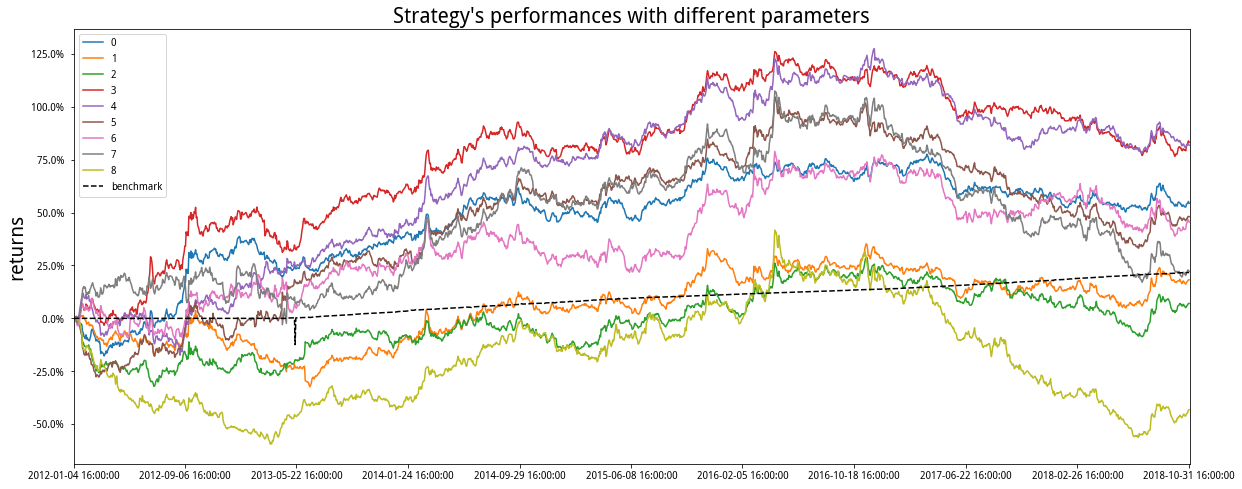
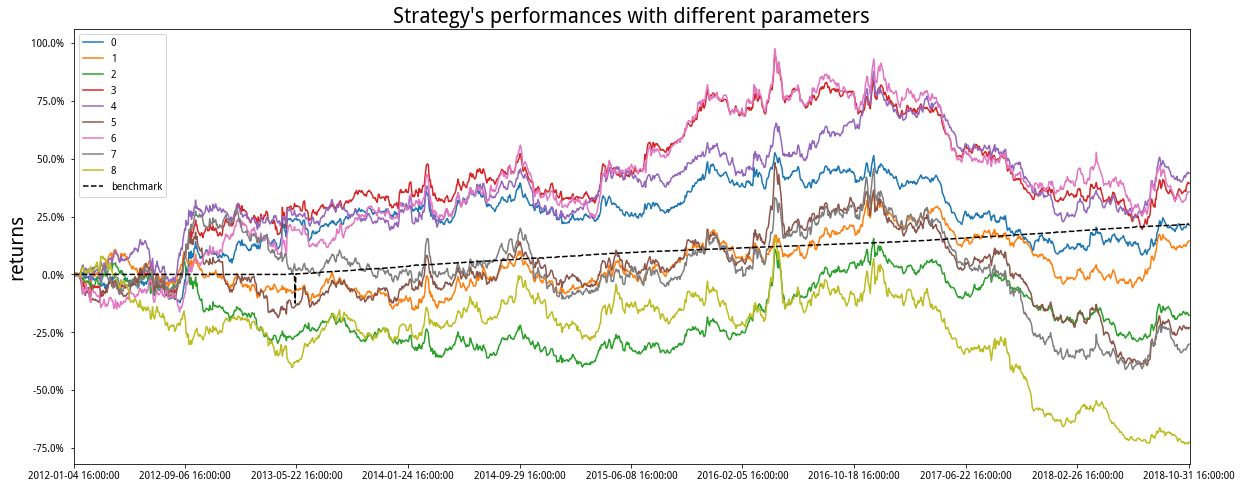
對於橫截面動量，在2017年開始的回撤比較顯著，並且在曆史上也沒有帶來非常理想的回報。我們測試了以5日為持有期，10、15、20這3組動量測算期的績效，並且測試了持有前20%，30%，40%的品種績效組合，也就是3*3=9個參數績效如下圖：

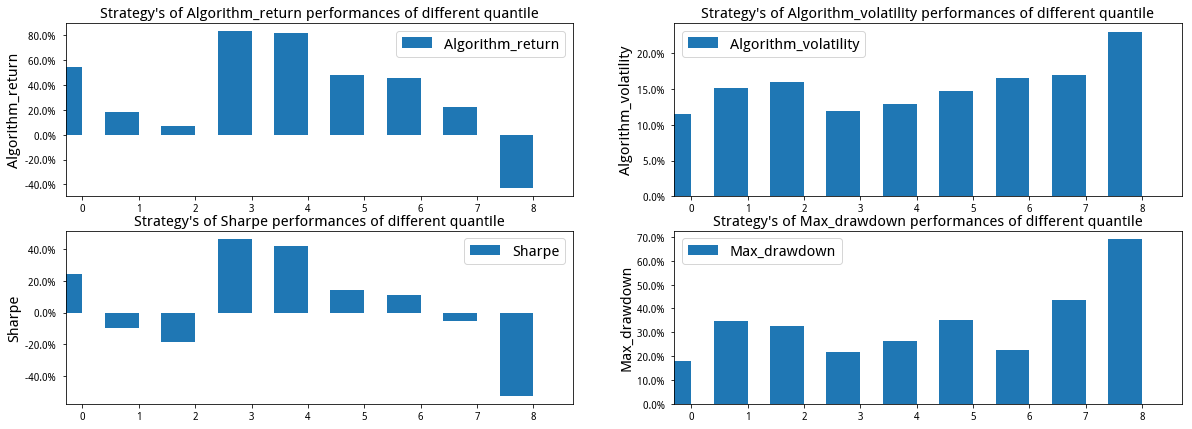
上圖分別是多組參數測試績效、資金曲線圖、收益風險矩陣。它們都是周度調倉，或者說接近研報上的5日調倉（持有）參數H。最終發現，做多前30%漲幅最多的品種，做空後30%跌幅最多的品種，持有5日，以10日考核期動量效應，這個組合績效最好。

我們還測試了雙周調倉，也就是每半個月調倉的效果，類似於研報中的10日調倉（持有）參數H，情況更不理想。

我們感覺還需要反複迭代或者思考的是：

1、多頭和空頭的動量衡量周期，是不是應該保持一致，還是應該拆分？
2、以較大的周期進行動量考核（某機構給出的250日動量考核期R參數）是否合理？
3、較為嚴格的止損方案，在較短周期的截面動量模型中，是否有效？

總之，還請大家多多提出意見，提出修改觀點，來完善這個多空都持有的比較另類的動量模型。