我们曾努力研究各种运用机器学习的方式,旨在发现外汇市场中的形态。 您已经知道如何训练模型并实现它们。 但还有很多交易方式,几乎每种方法都可以通过运用现代机器学习算法进行改进。 其中最流行的算法之一就是网格和/或马丁格尔。 在撰写本文之前,我做了一些探索性分析,在互联网上搜索相关信息。 令人惊讶的是,这种方法在全球网络中难觅踪迹。 我在社区成员中发起了一次有关此解决方案前景的调查,大多数人回答说他们甚至不知道如何入手该主题,但是这个想法听起来很有趣。 虽然,这个思路本身似乎很简单。
我们抱着两个目的来进行一系列实验。 首先,我们将尝试证明它并不像乍看起来那样困难。 其次,我们将尝试找出这种方式是否实用和有效。
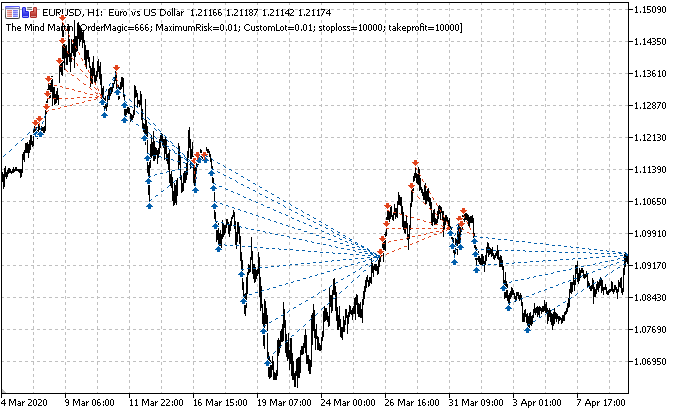
主要任务是正确地为成交贴标签。 我们还记得以前文章中如何处理单一仓位的。 我们设置了随机或确定性的成交边际,例如,15 根柱线。 如果行情在这 15 根柱线上都在上涨,则该成交被贴上标签“买入”,否则被贴上标签“卖出”。 类似的逻辑也运用在订单网格,但是此处必须考虑一组持仓的总盈利/亏损。 这可以用一个简单的例子来阐述。 作者会尽力描绘蓝图。
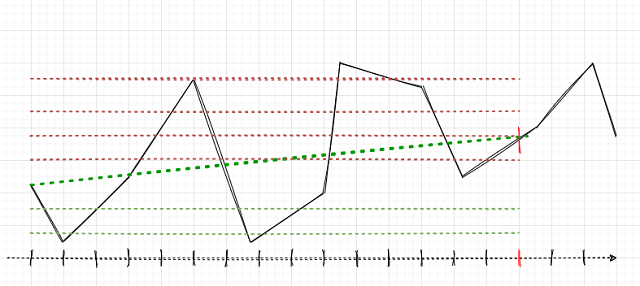
假设交易边际是15(十五)根柱线(在传统时间标尺上以垂直线标记的红色笔划)。 如果只有一笔持仓,由于行情已从一个点位上涨到另一个点位,故它将被贴上标签“买入”(绿色点划斜线)。 行情在此处显示为黑色折线。
有了这样的标签,过渡行情的波动即被忽略了。 如果我们运用订单网格(红色和绿色水平线),则必须计算所有已触发挂单的总利润,包括自最初开始的订单(您可在同一方向上开仓布局网格;或者选择放置挂单网格,无需即刻开仓)。 针对学习历史的整个深度,在滑动窗口中持续如此贴标签。 ML(机器学习)的任务是归纳各种状况,并基于新数据有效地预测(如果可能)。
在这种情况下,也许会有若干个选项用于选择交易方向,并为数据贴标签。 如何选择在此即是哲学也是实验任务。
这三条准测对于开始似乎已经足够了。 我们来详细研究第一个,因为它是最简单的一个,旨在获得最大的利润。
现在我们回想一下以前文章中如何为成交贴标签。
def add_labels(dataset, min, max): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index).reset_index(drop=True) return dataset
该代码需要针对常规网格和马丁格尔网格进行归纳。 另一个令人兴奋的功能是,您可以浏览含有不同数量订单的网格,订单之间的距离不同,甚至可以运用马丁格尔(手数递增)。
为此,我们添加全局变量,以后可用它来优化。
GRID_SIZE = 10 GRID_DISTANCES = np.full(GRID_SIZE, 0.00200) GRID_COEFFICIENTS = np.linspace(1, 3, num= GRID_SIZE)
GRID_SIZE 变量里包含双向订单的数量。
GRID_DISTANCES 设置订单之间的距离。 距离可以是固定的,亦或可变的(对于所有订单而言各有不同)。 这将有助于提升交易系统的灵活性。
GRID_COEFFICIENTS 变量包含每笔订单的手数乘数。 如果它们是常数,则系统将创建规则的网格。 如果手数不同,那么它会是马丁格尔或逆马丁格尔,或任何其他运用不同手数乘数的网格名称。
对于那些刚接触 numpy 函数库的人:
array([1. , 1.22222222, 1.44444444, 1.66666667, 1.88888889, 2.11111111, 2.33333333, 2.55555556, 2.77777778, 3. ])
相应地,第一个手数乘数将等于 1,因此该手数将等于交易系统参数中指定的基本手数。 在以后的网格里订单手数乘数连续从 1 到 3。 若在网格里的所有订单采用固定乘数,则需调用 np.full。
统计已触发和未触发订单可能有些棘手,故此我们需要创建某种数据结构。 我决定创建一本字典来保存每个特定案例(样本)的订单和仓位记录。 取而代之,我们可以利用数据类对象,熊猫数据框架或 numpy 结构化数组。 最后的解决方案,很可能是最快的,但在此它并不要紧。
每次迭代将样本添加到训练集合当中,并创建有关的订单网格信息,保存在字典里。 这可能需要一些解释。 grid_stats 字典包含有关当前订单网格从打开到平仓的所有必需信息。
def add_labels(dataset, min, max, distances, coefficients): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) all_pr = dataset['close'][i:i + rand + 1] grid_stats = {'up_range': all_pr[0] - all_pr.min(), 'dwn_range': all_pr.max() - all_pr[0], 'up_state': 0, 'dwn_state': 0, 'up_orders': 0, 'dwn_orders': 0, 'up_profit': all_pr[-1] - all_pr[0] - MARKUP, 'dwn_profit': all_pr[0] - all_pr[-1] - MARKUP } for i in np.nditer(distances): if grid_stats['up_state'] + i <= grid_stats['up_range']: grid_stats['up_state'] += i grid_stats['up_orders'] += 1 grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \ * coefficients[int(grid_stats['up_orders']-1)] grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)] if grid_stats['dwn_state'] + i <= grid_stats['dwn_range']: grid_stats['dwn_state'] += i grid_stats['dwn_orders'] += 1 grid_stats['dwn_profit'] += (all_pr[0] - all_pr[-1] + grid_stats['dwn_state']) \ * coefficients[int(grid_stats['dwn_orders']-1)] grid_stats['dwn_profit'] -= MARKUP * coefficients[int(grid_stats['dwn_orders']-1)] if grid_stats['up_profit'] > grid_stats['dwn_profit'] and grid_stats['up_profit'] > 0: labels.append(0.0) continue elif grid_stats['dwn_profit'] > 0: labels.append(1.0) continue labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index).reset_index(drop=True) return dataset
all_pr 变量包含从当前到未来的价格。 需要计算网格本身。 为了构建网格,我们想知道从第一根到最后一根柱线的价格范围。 这些值包含在 “up_range” 和 “dwn_range” 字典条目当中。 变量 “up_profit” 和 “dwn_profit” 将包含当前历史片段中的 “买入” 或 “卖出” 网格所获得的最终利润。 这些数值的初始值,来自最初开仓的一笔成交中获得的利润。 然后,如果网格挂单被触发,所有开单成交均会汇总。
现在,我们需要遍历所有 GRID_DISTANCES,并检查是否触发了挂单。 如果订单处于 up_range 或 dwn_range 范围内,则该订单已被触发。 在这种情况下,我们增加相应的 up_state 和 dwn_state 计数器,这些计数器存储最后一次激活订单的级别。 在下一次迭代中,网格中距新订单的距离会被添加到该级别 - 如果该订单在价格范围内,则它也已被触发。
所有已触发的订单均要编写附加信息。 例如,挂单的利润被添加到总数值之中。 对于买入仓位,此利润采用以下公式计算。 此处,用仓位的最后价格(应该是该仓位的平仓价)减去开仓价格,加上与系列中所选挂单的距离,并将结果乘以网格中该订单的手数乘数。 卖出订单则是逆计算。 累积的标记则会另外计算。
grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \ * coefficients[int(grid_stats['up_orders']-1)] grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)]
下一个代码模块检查买入和卖出网格的利润。 参考累计的标记,若利润大于零,且是最大值,则将相应的样本添加到训练集合当中。 如果不满足任何条件,则添加 2.0 标记 - 带有该标记的样本将从训练数据集合中删除,因为这代表它们是无用的。 这些条件可以以后更改,取决于所期望网格的构建选项。
为了正确地计算来自网格交易中获得的利润,我们需要修改策略测试器。 我决定令其类似于 MetaTrader 5 测试器,如此它即可顺序地遍历报价历史,并像真实交易一样开仓和平仓。 这样可以提升对代码的理解,并避免以后有所遗漏。 我将重点介绍代码的要点。 我不会在这里提供测试器旧版,但是您可以在我以前的文章中找到它。 我猜测有些读者可能不理解下面的代码,因为他们想快点拿到圣杯,不想啰嗦。 然而,关键点应予以澄清。
def tester(dataset, markup, distances, coefficients, plot=False): last_deal = int(2) all_pr = np.array([]) report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] all_pr = np.append(all_pr, dataset['close'][i]) if last_deal == 2: last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 1 up_range = all_pr[0] - all_pr.min() up_state = 0 up_orders = 0 up_profit = (all_pr[-1] - all_pr[0]) - markup report.append(report[-1] + up_profit) up_profit = 0 for d in np.nditer(distances): if up_state + d <= up_range: up_state += d up_orders += 1 up_profit += (all_pr[-1] - all_pr[0] + up_state) \ * coefficients[int(up_orders-1)] up_profit -= markup * coefficients[int(up_orders-1)] report.append(report[-1] + up_profit) up_profit = 0 all_pr = np.array([dataset['close'][i]]) continue if last_deal == 1 and pred < 0.5: last_deal = 0 dwn_range = all_pr.max() - all_pr[0] dwn_state = 0 dwn_orders = 0 dwn_profit = (all_pr[0] - all_pr[-1]) - markup report.append(report[-1] + dwn_profit) dwn_profit = 0 for d in np.nditer(distances): if dwn_state + d <= dwn_range: dwn_state += d dwn_orders += 1 dwn_profit += (all_pr[0] + dwn_state - all_pr[-1]) \ * coefficients[int(dwn_orders-1)] dwn_profit -= markup * coefficients[int(dwn_orders-1)] report.append(report[-1] + dwn_profit) dwn_profit = 0 all_pr = np.array([dataset['close'][i]]) continue y = np.array(report).reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.figure(figsize=(12,7)) plt.plot(report) plt.plot(lr.predict(X)) plt.title("Strategy performance") plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
纵观历史,网格交易者仅对余额曲线感兴趣,而往往忽视净值曲线。 因此,我们将坚持这一传统,且不会令我们复杂的测试仪变得过于复杂。 我们将仅显示余额图形。 进而,净值曲线可始终在 MetaTrader 5 终端中查看。
我们循环遍历所有价格,并将它们添加到数组 all_pr。 此外,上面标记了三个选项。 由于以前的文章中已经讨论过该测试器,因此,我仅解释出现相反信号时网格平单的选项。 就像在为成交贴标签时一样,up_range 变量存储按平仓时间的价格范围。 接下来,计算第一笔仓位(按市价开仓)的利润。 然后,循环检查是否存在已触发挂单。 如果有,则将其结果添加到余额图形中。 卖出订单/仓位也需执行相同的操作。 因此,余额图形反映的是所有已平仓位,而不是一组的总利润。
我们已经很熟悉如何为机器学习准备数据。 首先获取价格和一套功能,然后为数据贴标签(创建“买入”和“卖出”标签),然后在自定义测试器中检查标签。
# Get prices and labels and test it pr = get_prices(START_DATE, END_DATE) pr = add_labels(pr, 15, 15, GRID_DISTANCES, GRID_COEFFICIENTS) tester(pr, MARKUP, GRID_DISTANCES, GRID_COEFFICIENTS, plot=True)
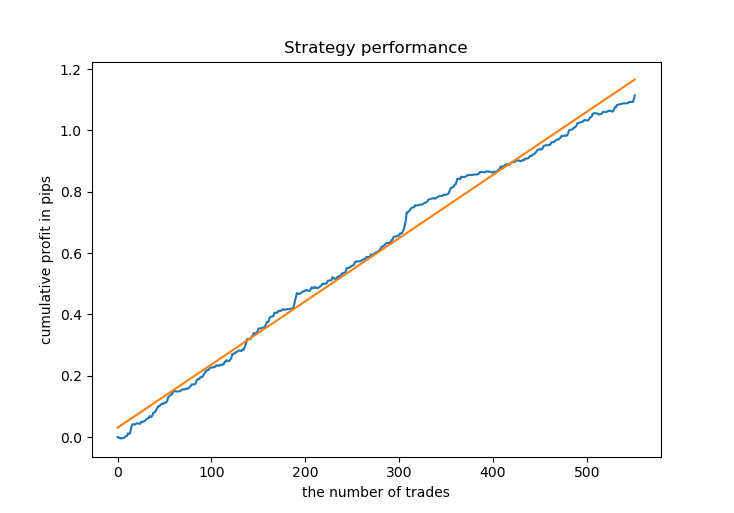
现在,我们需要训练 CatBoost 模型,并依据新数据对其进行测试。 由于其效果良好,我决定再次依据高斯混合模型生成的合成数据进行训练。
# Learn and test CatBoost model gmm = mixture.GaussianMixture( n_components=N_COMPONENTS, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) res = [] for i in range(10): res.append(brute_force(10000)) print('Iteration: ', i, 'R^2: ', res[-1][0]) res.sort() test_model(res[-1])
在此示例中,我们将依据 10,000 个生成的样本上训练 10 个模型,并通过 R^2 分数选择最佳的一个模型。 学习过程如下。
Iteration: 0 R^2: 0.8719436661855786 Iteration: 1 R^2: 0.912006346274096 Iteration: 2 R^2: 0.9532278725035132 Iteration: 3 R^2: 0.900845571741786 Iteration: 4 R^2: 0.9651728908727953 Iteration: 5 R^2: 0.966531822300101 Iteration: 6 R^2: 0.9688263099200539 Iteration: 7 R^2: 0.8789927823514787 Iteration: 8 R^2: 0.6084261786804662 Iteration: 9 R^2: 0.884741078512629
大多数模型在新数据上的 R^2 分数都很高,这表明该模型具有很高的稳定性。 这是训练数据和训练外数据的余额图结果。
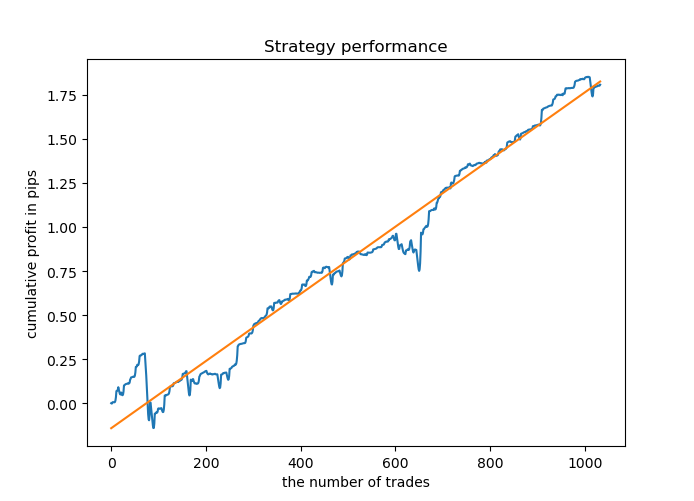
看起来不错。 现在,我们可以导出经过 MetaTrader 5 训练的模型,并在终端测试器中检查其结果。 在测试之前,有必要准备智能交易系统,并包含文件。 每个训练过的模型都有其自己的文件,因此可以轻松存储和更改它们。
调用以下函数来导出模型。
export_model_to_MQL_code(res[-1][1])
该函数已稍作修改。 针对修改的解释如下。
def export_model_to_MQL_code(model):
model.save_model('catmodel.h',
format="cpp",
export_parameters=None,
pool=None)
# add variables
code = '#include <Math\Stat\Math.mqh>'
code += '\n'
code += 'int MAs[' + str(len(MA_PERIODS)) + \
'] = {' + ','.join(map(str, MA_PERIODS)) + '};'
code += '\n'
code += 'int grid_size = ' + str(GRID_SIZE) + ';'
code += '\n'
code += 'double grid_distances[' + str(len(GRID_DISTANCES)) + \
'] = {' + ','.join(map(str, GRID_DISTANCES)) + '};'
code += '\n'
code += 'double grid_coefficients[' + str(len(GRID_COEFFICIENTS)) + \
'] = {' + ','.join(map(str, GRID_COEFFICIENTS)) + '};'
code += '\n'
# get features
code += 'void fill_arays( double &features[]) {\n'
code += ' double pr[], ret[];\n'
code += ' ArrayResize(ret, 1);\n'
code += ' for(int i=ArraySize(MAs)-1; i>=0; i--) {\n'
code += ' CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr);\n'
code += ' double mean = MathMean(pr);\n'
code += ' ret[0] = pr[MAs[i]-1] - mean;\n'
code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
code += ' ArraySetAsSeries(features, true);\n'
code += '}\n\n'
# add CatBosst
code += 'double catboost_model' + '(const double &features[]) { \n'
code += ' '
with open('catmodel.h', 'r') as file:
data = file.read()
code += data[data.find("unsigned int TreeDepth")
:data.find("double Scale = 1;")]
code += '\n\n'
code += 'return ' + \
'ApplyCatboostModel(features, TreeDepth, TreeSplits , BorderCounts, Borders, LeafValues); } \n\n'
code += 'double ApplyCatboostModel(const double &features[],uint &TreeDepth_[],uint &TreeSplits_[],uint &BorderCounts_[],float &Borders_[],double &LeafValues_[]) {\n\
uint FloatFeatureCount=ArrayRange(BorderCounts_,0);\n\
uint BinaryFeatureCount=ArrayRange(Borders_,0);\n\
uint TreeCount=ArrayRange(TreeDepth_,0);\n\
bool binaryFeatures[];\n\
ArrayResize(binaryFeatures,BinaryFeatureCount);\n\
uint binFeatureIndex=0;\n\
for(uint i=0; i<FloatFeatureCount; i++) {\n\
for(uint j=0; j<BorderCounts_[i]; j++) {\n\
binaryFeatures[binFeatureIndex]=features[i]>Borders_[binFeatureIndex];\n\
binFeatureIndex++;\n\
}\n\
}\n\
double result=0.0;\n\
uint treeSplitsPtr=0;\n\
uint leafValuesForCurrentTreePtr=0;\n\
for(uint treeId=0; treeId<TreeCount; treeId++) {\n\
uint currentTreeDepth=TreeDepth_[treeId];\n\
uint index=0;\n\
for(uint depth=0; depth<currentTreeDepth; depth++) {\n\
index|=(binaryFeatures[TreeSplits_[treeSplitsPtr+depth]]<<depth);\n\
}\n\
result+=LeafValues_[leafValuesForCurrentTreePtr+index];\n\
treeSplitsPtr+=currentTreeDepth;\n\
leafValuesForCurrentTreePtr+=(1<<currentTreeDepth);\n\
}\n\
return 1.0/(1.0+MathPow(M_E,-result));\n\
}'
file = open('C:/Users/dmitrievsky/AppData/Roaming/MetaQuotes/Terminal/D0E8209F77C8CF37AD8BF550E51FF075/MQL5/Include/' +
str(SYMBOL) + '_cat_model_martin' + '.mqh', "w")
file.write(code)
file.close()
print('The file ' + 'cat_model' + '.mqh ' + 'has been written to disc')
现在可以保存训练中所用的网格设置。 它们将会在交易时用到。
来自标准终端发布包的移动平均线和指标缓冲区,已不再使用。 取而代之,所有功能都在函数主体中计算。 添加原始功能时,也应在导出的函数里添加这些功能。
绿色高亮示意终端的 “Include” 文件夹的路径。 它允许保存 .mqh 文件,并将其连接到智能交易系统。
我们来查看 .mqh 文件本身(此处省略了 CatBoost 模型)
#include <Math\Stat\Math.mqh> int MAs[14] = {5,25,55,75,100,125,150,200,250,300,350,400,450,500}; int grid_size = 10; double grid_distances[10] = {0.003,0.0035555555555555557,0.004111111111111111,0.004666666666666666,0.005222222222222222, 0.0057777777777777775,0.006333333333333333,0.006888888888888889,0.0074444444444444445,0.008}; double grid_coefficients[10] = {1.0,1.4444444444444444,1.8888888888888888,2.333333333333333, 2.7777777777777777,3.2222222222222223,3.6666666666666665,4.111111111111111,4.555555555555555,5.0}; void fill_arays( double &features[]) { double pr[], ret[]; ArrayResize(ret, 1); for(int i=ArraySize(MAs)-1; i>=0; i--) { CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr); double mean = MathMean(pr); ret[0] = pr[MAs[i]-1] - mean; ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); } ArraySetAsSeries(features, true); }
如您所见,所有网格设置均已保存,模型已准备就绪。 您仅需将其连接到智能交易系统即可。
#include <EURUSD_cat_model_martin.mqh> 现在,我要解释智能交易系统处理信号所依据的逻辑。 以 OnTick() 函数为例。 该机器人用到了 MT4Orders 函数库,该函数库需另行下载。
void OnTick() { //--- if(!isNewBar()) return; TimeToStruct(TimeCurrent(), hours); double features[]; fill_arays(features); if(ArraySize(features) !=ArraySize(MAs)) { Print("No history available, will try again on next signal!"); return; } double sig = catboost_model(features); // Close positions by an opposite signal if(count_market_orders(0) || count_market_orders(1)) for(int b = OrdersTotal() - 1; b >= 0; b--) if(OrderSelect(b, SELECT_BY_POS) == true) { if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5) if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) { } if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5) if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) { } } // Delete all pending orders if there are no pending orders if(!count_market_orders(0) && !count_market_orders(1)) { for(int b = OrdersTotal() - 1; b >= 0; b--) if(OrderSelect(b, SELECT_BY_POS) == true) { if(OrderType() == 2 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic ) if(OrderDelete(OrderTicket())) { } if(OrderType() == 3 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic ) if(OrderDelete(OrderTicket())) { } } } // Open positions and pending orders by signals if(countOrders() == 0 && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) { double l = LotsOptimized(); if(sig < 0.5) { OrderSend(Symbol(),OP_BUY,l, Ask, 0, Bid-stoploss*_Point, Ask+takeprofit*_Point, NULL, OrderMagic); double p = Ask; for(int i=0; i<grid_size; i++) { p = NormalizeDouble(p - grid_distances[i], _Digits); double gl = NormalizeDouble(l * grid_coefficients[i], 2); OrderSend(Symbol(),OP_BUYLIMIT,gl, p, 0, p-stoploss*_Point, p+takeprofit*_Point, NULL, OrderMagic); } } else { OrderSend(Symbol(),OP_SELL,l, Bid, 0, Ask+stoploss*_Point, Bid-takeprofit*_Point, NULL, OrderMagic); double p = Ask; for(int i=0; i<grid_size; i++) { p = NormalizeDouble(p + grid_distances[i], _Digits); double gl = NormalizeDouble(l * grid_coefficients[i], 2); OrderSend(Symbol(),OP_SELLLIMIT,gl, p, 0, p+stoploss*_Point, p-takeprofit*_Point, NULL, OrderMagic); } } } }
fill_arrays 函数为 CatBoost 模型提供填充 features 数组的功能。 然后将此数组传递给 catboost_model() 函数,该函数返回 0;1 范围的信号。
如您从买入订单示例中所见,这里用到了 grid_size 变量。 它示意了挂单的数量,这些订单位于 grid_distances 的距离上。 标准手数乘以 grid_coefficients 数组中的系数,该系数与订单号相对应。
机器人经编译之后,我们就可进行测试了。
测试应在机器人所训练的时间帧内进行。 在这种情况下,它是 H1。 可以采用开盘价对其进行测试,因为该机器人对于柱线开盘拥有明确的控制权。 不过,由于运用的是网格,因此可以选择 M1 OHLC 来获得更高的精度。
该特定的机器人已在以下周期内经历了训练:
START_DATE = datetime(2020, 5, 1) TSTART_DATE = datetime(2019, 1, 1) FULL_DATE = datetime(2018, 1, 1) END_DATE = datetime(2022, 1, 1)
所有这些因素表明(并经自定义测试器确认)我们在从 2018 年到今天的区间中找到了某种形态。
我们来看看在 MetaTrader 5 策略测试器中它的样子。
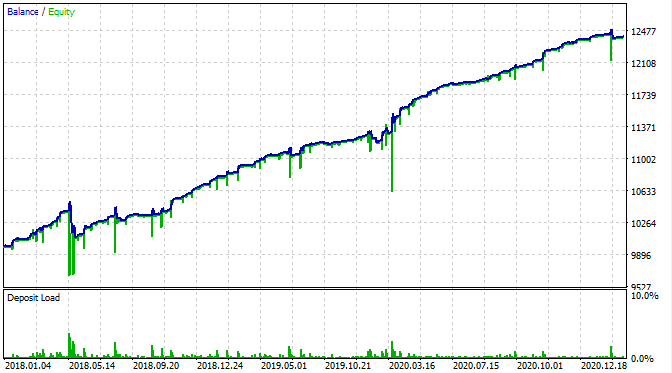
除了我们现在可以看到净值回撤以外,余额图的图表与我的自定义测试器相同。 这是个好消息。 我们来确保该机器人正在遵照网格正确交易,且无其他干扰。
这是从 2015 年开始的测试结果。
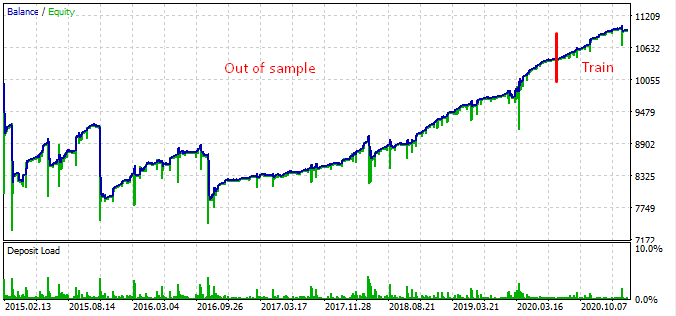
根据该图形,找到的形态从 2016 年底到今天有效,而在其余时间区间则失效。 在这种情况下,初始手数很少,这有助于该机器人得以生存。 至少我们知道该机器人自 2017 年初以来一直有效。 有基于此,我们可以增加风险,以期提高盈利效果。 该机器人展现出令人印象深刻的结果:3 年内达到 1600%,回撤 40%,有亏损全部本金的风险。
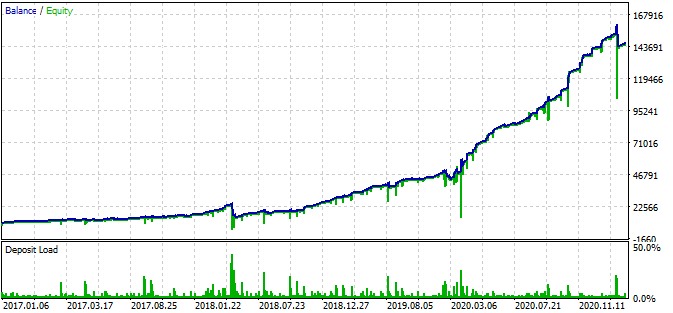
此外,机器人在每笔持仓里使用了止损和止盈。 使用 SL 和 TP 会牺牲性,但同时能限制风险。
请注意,我采用了非常激进的网格。
GRID_COEFFICIENTS = np.linspace(1, 5, num= GRID_SIZE)
array([1. , 1.44444444, 1.88888889, 2.33333333, 2.77777778, 3.22222222, 3.66666667, 4.11111111, 4.55555556, 5. ])
最后的乘数等于 5。 这意味着该系列中最后一笔订单的手数比初始手数高五倍,这带来了额外的风险。 您可以选择更多稳妥的模式。
为什么该机器人在 2016 年或更早的时间内会停止工作? 对于这个问题,我没有任何有意义的答案。 似乎在外汇市场上有很长的七年周期,或者较短周期,它们彼此的形态毫无关联。 这是一个单独的主题,需要进行更详细的研究。
在本文中,我尝试讲述可用于训练模型或神经网络,提升其马丁格尔交易能力的技术。 本文介绍了一种现成的解决方案,您可参考它来创建自己的交易机器人。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
