在 2018 年 6 月,OpenAI 提出了 GPT 神经网络模型,该模型立即在多种语言类测试中展现出极佳结果。 GDP-2 于 2019 年出现,而 GPT-3 则于 2020 年 5 月提出。 这些模型展示了神经网络生成相关文本的能力。 尚有其他实验涉及生成音乐和图像的能力。 这一模型的主要缺点与它们涉及的计算资源相关。 在配备 8 颗 GPU 的计算机上训练第一个 GPT 花费了一个月的时间。 为了解决新问题,使用预先训练的模型,可部分弥补这一缺陷。 但考虑到模型的规模,需要大量资源来维持模型的运行。
从概念来讲,GPT 模型是在之前研究的变换器基础上构建的。 主要思路是基于大数据针对模型进行无监督预训练,然后再依据相对少量的标记数据进行微调。
分两步训练的原因在于模型规模。 像 GPT 这样的现代深度机器学习模型涉及大量参数,可多达数亿个。 因此,这种神经网络的训练需要大量的训练样本。 当采用监督学习时,创建带标记的训练样本集合是件劳动密集型工作。 与此同时,网站上有许多不同的数字化和无标记文本,这些文本非常适合模型的无监督训练。 然而,统计数据表明,无监督学习相较监督学习,其结果要差很多。 因此,在无监督训练之后,可依据相对少量的标记数据样本针对模型进行微调。
无监督学习可令 GPT 学习语言类模型,而针对特定任务,可依据标记数据进一步训练,从而调整模型。 因此,为了执行不同的语言类任务,可以复制并微调一个预训练的模型。 该限制基于采用无监督学习的原始语言集合。
实践表明,这种方法对于广泛的语言问题能产生良好的效果。 例如,GPT-3 模型能够针对给定主题生成连贯流畅的文本。 不过,请注意,指定的模型包含 1750 亿个参数,按顺序依据 570GB 的数据集合上进行了预训练。
尽管 GPT 模型是为处理自然语言类而开发的,但它们在音乐和图像生成任务中也表现出色。
理论上,GPT 模型可与任何数字化数据序列配合使用。 唯一的前置需求是无监督的预学习需要足够的数据和资源。
我们来研究 GPT 模型与之前研究的变换器有何区别。 首先,GPT 模型未使用编码器,因为它们仅使用解码器。 当没有编码器时,模型不再拥有“编码器 - 解码器自关注”内层。 下图展示了 GPT 变换器模块。
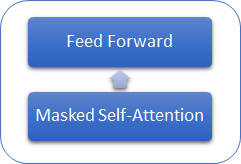
与经典的变换器相似,GPT 模型中的模块在彼此之上构建。 每个模块针对关注机制都有自己的权重矩阵,并具有完全连接的前馈层。 模块的数量决定了模型的规模。 模块堆栈可能会很庞大。 GPT-1 和最小的 GPT-2(小型 GPT-2)有 12 个模块;GPT-2 特大型有 48 个,而 GPT-3 则有 96 个模块。
与传统语言类模型类似,GPT 仅能够发现与序列中先前元素的关系,但无法窥视未来。 但它与变换器不同,GPT 不使用元素的掩码 — 代之,它更改了计算过程。 GPT 会重置 Score 矩阵中后续元素的关注比率。
同时,GPT 可被归类为自回归模型。 每次迭代都会生成一个序列令牌。 生成的令牌会被添加到输入序列中,并馈入模型进行下一次迭代。
与经典变换器一样,自关注机制内的每个令牌都会生成三个向量:一个 query,一个 key,和一个 value。 在自回归模型当中,在每次新迭代里,输入序列仅能由 1 个令牌更改,因此每个令牌无需重新计算向量。 因此,GPT 中的每一层只在序列有新元素时计算向量。 每个变换器模块都保存其向量,以备后用。
这种方式令模型能够在接收最终令牌之前逐词生成文本。
当然,GPT 模型采用多目击者关注机制。
在开始之前,我们来简要地复习一下算法:
针对所有自关注目击者的一个序列。 进而,对于每个关注的目击者,2-5 中的动作是相同的。
作为第 3 步和第 4 步的结果,我们获得了平方矩阵 Score,该平方矩阵的大小依据序列中元素的数量来确定,在其内每个 'query' 的上下文中所有元素的合计为 “1”。
为了实现我们的模型,我们在 CNeuronBaseOCL 基类的基础上创建一个新类 CNeuronMLMHAttentionOCL。 我故意退后一步,且没有使用之前创建的关注类。 这是因为目前我们采用了新的“多目击者自关注”创建原理。 早前,在文章第十部分中,我们创建了 CNeuronMHAttentionOCL 类,该类可顺序提供 4 个关注线程的重新计算。 线程数量在方法里是硬编码的,因此更改线程数量会需要大量工时,这会涉及修改类及其方法的相关代码。
警告。 如上所述,GPT 模型采用含有相同(不可更改)超参数的相同变换器模块的堆栈,唯一的区别在于其所正在训练的矩阵。 因此,我决定创建一个多层模块,它允许创建带有超参数的模型,在创建类时这些模型可作为传递参数。 这包括堆栈中变换器模块的重复次数。
结果就是,我们有了一个类,它可基于一些指定的参数来创建几乎整个模型。 因此,在新类的“保护”部分中,我们声明五个变量来存储模块参数:
| iLayers | 模型中的变换器模块数量 |
| iHeads | 自关注目击者的数量 |
| iWindow | 输入窗口大小(1 个输入序列令牌) |
| iWindowKey | 内部向量 Query、Key、Value 的维度 |
| iUnits | 输入序列中的元素(令牌)数量 |
还有,在受保护部分中,声明 6 个数组,来存储缓冲区集合,其内是我们的张量和训练权重矩阵:
| QKV_Tensors | 存储张量 Query、Key、Value,及其梯度的数组 |
| QKV_Weights | 存储 Wq、Wk、Wv 权重矩阵、及其动量矩阵集合的数组 |
| S_Tensors | 存储 Score 矩阵、及其梯度集合的数组 |
| AO_Tensors | 存储自关注机制输出张量、及其梯度的数组 |
| FF_Tensors | 存储前馈模块输入、隐藏和输出张量、及其梯度的数组 |
| FF_Weights | 存储前馈模块权重矩阵、及其动量的数组。 |
我们将在以后实现它们时,再研究该类方法。
class CNeuronMLMHAttentionOCL : public CNeuronBaseOCL { protected: uint iLayers; ///< Number of inner layers uint iHeads; ///< Number of heads uint iWindow; ///< Input window size uint iUnits; ///< Number of units uint iWindowKey; ///< Size of Key/Query window //--- CCollection *QKV_Tensors; ///< The collection of tensors of Queries, Keys and Values CCollection *QKV_Weights; ///< The collection of Matrix of weights to previous layer CCollection *S_Tensors; ///< The collection of Scores tensors CCollection *AO_Tensors; ///< The collection of Attention Out tensors CCollection *FF_Tensors; ///< The collection of tensors of Feed Forward output CCollection *FF_Weights; ///< The collection of Matrix of Feed Forward weights ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::FeedForward().@param NeuronOCL Pointer to previos layer. virtual bool ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ); ///< \brief Convolution Feed Forward method of calling kernel ::FeedForwardConv(). virtual bool AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true); ///< \brief Multi-heads attention scores method of calling kernel ::MHAttentionScore(). virtual bool AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out); ///< \brief Multi-heads attention out method of calling kernel ::MHAttentionOut(). virtual bool SumAndNormilize(CBufferDouble *tensor1, CBufferDouble *tensor2, CBufferDouble *out); ///< \brief Method sum and normalize 2 tensors by calling 2 kernels ::SumMatrix() and ::Normalize(). ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateWeightsMomentum() or ::UpdateWeightsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previos layer. virtual bool ConvolutuionUpdateWeights(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *momentum1, CBufferDouble *momentum2, uint window, uint window_out); ///< Method for updating weights in convolution layer.\details Calling one of kernels ::UpdateWeightsConvMomentum() or ::UpdateWeightsConvAdam() in depends on optimization type (#ENUM_OPTIMIZATION). virtual bool ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ); ///< Method of passing gradients through a convolutional layer. virtual bool AttentionInsideGradients(CBufferDouble *qkv,CBufferDouble *qkv_g,CBufferDouble *scores,CBufferDouble *scores_g,CBufferDouble *gradient); ///< Method of passing gradients through attention layer. public: /** Constructor */CNeuronMLMHAttentionOCL(void); /** Destructor */~CNeuronMLMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMLMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
在类的构造函数当中,我们为类的超参数设置初始值,并初始化集合数组。
CNeuronMLMHAttentionOCL::CNeuronMLMHAttentionOCL(void) : iLayers(0), iHeads(0), iWindow(0), iWindowKey(0), iUnits(0) { QKV_Tensors=new CCollection(); QKV_Weights=new CCollection(); S_Tensors=new CCollection(); AO_Tensors=new CCollection(); FF_Tensors=new CCollection(); FF_Weights=new CCollection(); }
相应地,我们类的析构函数中的集合数组删除了。
CNeuronMLMHAttentionOCL::~CNeuronMLMHAttentionOCL(void) { if(CheckPointer(QKV_Tensors)!=POINTER_INVALID) delete QKV_Tensors; if(CheckPointer(QKV_Weights)!=POINTER_INVALID) delete QKV_Weights; if(CheckPointer(S_Tensors)!=POINTER_INVALID) delete S_Tensors; if(CheckPointer(AO_Tensors)!=POINTER_INVALID) delete AO_Tensors; if(CheckPointer(FF_Tensors)!=POINTER_INVALID) delete FF_Tensors; if(CheckPointer(FF_Weights)!=POINTER_INVALID) delete FF_Weights; }
类的初始化,以及模型的构建是在 Init 方法当中执行。 该方法会从参数里接收:
| numOutputs | 后续一层中所需创建链接的元素数量 |
| myIndex | 层中的神经元索引 |
| open_cl | OpenCL 对象指针 |
| window | 输入窗口大小(输入序列令牌) |
| window_key | 内部向量 Query、Key、Value 的维度 |
| heads | 自关注目击者(线程)数量 |
| units_count | 输入序列中的元素数量 |
| layers | 在模型堆栈中的模块(层)数量 |
| optimization_type | 在训练期间的参数优化方法 |
bool CNeuronMLMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint window_key,uint heads,uint units_count,uint layers,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,window*units_count,optimization_type)) return false; //--- iWindow=fmax(window,1); iWindowKey=fmax(window_key,1); iUnits=fmax(units_count,1); iHeads=fmax(heads,1); iLayers=fmax(layers,1);
在方法伊始,我们调用相应的方法来初始化父类。 请注意,我们没有执行基础的检查来验证所收到的 OpenCL 对象指针,和输入序列的大小,因为这些检查已在父类方法中实现。
成功初始化父类之后,我们将超参数保存到相应的变量当中。
接着,我们计算所要创建的张量大小。 请注意,以前的组织多目击者关注的修改方式。 我们不会为 'query'、'key' 和 'value' 向量创建单独的数组 - 它们将合并到一个数组。 进而,我们不会为每个关目击者创建单独的数组。 代之,我们将为 QKV(query + key + value)、Scores和自关注机制的输出创建通用数组。 这些元素将在张量中的索引级别切分为序列。 当然,这种方式更难以理解。 在张量中查找所需元素也许会更加困难。 但是,它能令模型变得更灵活,根据关注目击者的数量,并依据内核级别的并行线程来组织规划所有关注目击者的并发重新计算。
QKV_Tensor(数字)张量的大小定义为内部向量(query + key + value)的三个大小与目击者数量的乘积。 级联权重矩阵 QKV_Weight 的大小定义为输入序列令牌的三个大小的乘积,并依据偏移元素、内部向量的大小和关注目击者数量递增。 与此类似,我们计算剩余张量的大小。
uint num=3*iWindowKey*iHeads*iUnits; //Size of QKV tensor uint qkv_weights=3*(iWindow+1)*iWindowKey*iHeads; //Size of weights' matrix of QKV tensor uint scores=iUnits*iUnits*iHeads; //Size of Score tensor uint mh_out=iWindowKey*iHeads*iUnits; //Size of multi-heads self-attention uint out=iWindow*iUnits; //Size of our tensor uint w0=(iWindowKey+1)*iHeads*iWindow; //Size W0 tensor uint ff_1=4*(iWindow+1)*iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2=(4*iWindow+1)*iWindow; //Size of weights' matrix 2-nd feed forward layer
断定所有张量的大小之后,依据模块中关注层的数量运行一个循环,创建必要的张量。 请注意,在循环体内规划了两个嵌套循环。 第一重循环为 value 张量及其梯度创建数组。 第二重为权重矩阵及其矩创建数组。 请注意,对于最后一层,不会为前馈块输出张量及其梯度创建新的数组。 代之,将指向父类输出和梯度数组的指针加到集合之中。 如此简单的步骤避免了在数组之间传递数值的不必要迭代,并且消除了不必要的内存消耗。
for(uint i=0; i<iLayers; i++) { CBufferDouble *temp=NULL; for(int d=0; d<2; d++) { //--- Initialize QKV tensor temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(num,0)) return false; if(!QKV_Tensors.Add(temp)) return false; //--- Initialize scores temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(scores,0)) return false; if(!S_Tensors.Add(temp)) return false; //--- Initialize multi-heads attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(mh_out,0)) return false; if(!AO_Tensors.Add(temp)) return false; //--- Initialize attention out temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 1 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(4*out,0)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i==iLayers-1) { if(!FF_Tensors.Add(d==0 ? Output : Gradient)) return false; continue; } temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(out,0)) return false; if(!FF_Tensors.Add(temp)) return false; } //--- Initialize QKV weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; for(uint w=0; w<qkv_weights; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!QKV_Weights.Add(temp)) return false; //--- Initialize Weights0 temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w=0; w<w0; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; for(uint w=0; w<ff_1; w++) { if(!temp.Add(GenerateWeight())) return false; } if(!FF_Weights.Add(temp)) return false; //--- for(int d=0; d<(optimization==SGD ? 1 : 2); d++) { temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights,0)) return false; if(!QKV_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(w0,0)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initialize FF Weights temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_1,0)) return false; if(!FF_Weights.Add(temp)) return false; temp=new CBufferDouble(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.BufferInit(ff_2,0)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
结果就是,对于每一层,我们获得以下张量矩阵。
| QKV_Tensor |
|
| S_Tensors |
|
| AO_Tensors |
|
| FF_Tensors |
|
| QKV_Weights |
|
| FF_Weights |
|
创建数组集合之后,以“true” 退出方法。 附件中提供了所有类及其方法的完整代码。
传统上,前馈是在 feedForward 方法中组织的,该方法在参数中接收指向神经网络上一层的指针。 在方法开始时,检查所接收指针的有效性。
bool CNeuronMLMHAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false;
接着,我们规划一个循环来重新计算模块的所有层。 不像先前所述的其他类的类似方法,该方法是顶层的。 经简化的操作规划,准备数据和调用辅助方法(下面将讲述这些方法的逻辑)。
在循环伊始,我们从集合中接收与当前层相对应的 QKV 和 QKV_Weights 张量的输入数据缓冲区。 然后我们调用 ConvolutionForward 来计算向量 Query、Key 和 Value。
for(uint i=0; (i<iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferDouble *inputs=(i==0? NeuronOCL.getOutput() : FF_Tensors.At(6*i-4)); CBufferDouble *qkv=QKV_Tensors.At(i*2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),inputs,qkv,iWindow,3*iWindowKey*iHeads,None)) return false;
当增加关注层时,我遇到了一些障碍。 在某个点,我收到错误 5113 ERR_OPENCL_TOO_MANY_OBJECTS。 因此,我不得不考虑把所有张量永久存储在 GPU 内存之中。 故此,完成操作后,我释放了将在此步骤中不再使用的缓冲区。 在您的代码中,不要忘记从 GPU 内存的已释放缓冲区里读取最后的数据。 在本文所提供的类中,缓冲区数据是通过内核初始化方法读取的,稍后我们将进行讨论。
CBufferDouble *temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree();
与此类似,调用相应的方法计算“自关注”机制值的关注分数和权重矢量。
//--- Score calculation temp=S_Tensors.At(i*2); if(IsStopped() || !AttentionScore(qkv,temp,true)) return false; //--- Multi-heads attention calculation CBufferDouble *out=AO_Tensors.At(i*2); if(IsStopped() || !AttentionOut(qkv,temp,out)) return false; qkv.BufferFree(); temp.BufferFree();
在计算“多目击者关注”之后,将级联的关注输出折叠为输入序列大小,添加两个向量,并对结果进行常规化。
//--- Attention out calculation temp=FF_Tensors.At(i*6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out,temp,iWindowKey*iHeads,iWindow,None)) return false; out.BufferFree(); //--- Sum and normalize attention if(IsStopped() || !SumAndNormilize(temp,inputs,temp)) return false; if(i>0) inputs.BufferFree();
变换器中的自关注机制后面是由两个完全连接层组成的前馈模块。 然后,将结果添加到输入序列当中。 最终的张量在常规化馈入下一层。 在我们的情况下,我们终止了循环。
//--- Feed Forward inputs=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),inputs,temp,iWindow,4*iWindow,LReLU)) return false; out=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); out.BufferFree(); out=FF_Tensors.At(i*6+2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),temp,out,4*iWindow,iWindow,activation)) return false; temp.BufferFree(); temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); //--- Sum and normalize out if(IsStopped() || !SumAndNormilize(out,inputs,out)) return false; inputs.BufferFree(); } //--- return true; }
完整的方法代码在下面的附件中提供。 现在,我们研究从 FeedForward 方法调用辅助方法。 我们调用的第一个方法是 ConvolutionForward。 它在前馈方法的每个周期里调用四次。 在方法主体中,调用卷积层的前向传递内核。 在这种情况下,对于输入序列的每个单独令牌,该方法扮演的是完全连接层的角色。 该解决方案在文章第八部分中进行了更详细的讨论。 与前面讲述的解决方案相比,新方法从参数里接收指向缓冲区的指针,以便传输数据到 OpenCL 内核。 因此,在方法开始时,我们会检查所收指针的有效性。
bool CNeuronMLMHAttentionOCL::ConvolutionForward(CBufferDouble *weights, CBufferDouble *inputs,CBufferDouble *outputs, uint window, uint window_out, ENUM_ACTIVATION activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(outputs)==POINTER_INVALID) return false;
接下来,我们在 GPU 内存中创建缓冲区,并将必要的信息传递给它们。
if(!weights.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!outputs.BufferCreate(OpenCL)) return false;
后随文章第八部分中讲述的代码,未进行任何更改。 所调用的内核按原样使用,没有任何更改。
uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=outputs.Total()/window_out; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,outputs.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,inputs.Total()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,window); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,window_out); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activ); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardConv: %d",GetLastError()); return false; } //--- return outputs.BufferRead(); }
进而,feedForward 方法代码中调用了 AttentionScore 方法,该方法调用内核,计算并常规化关注分数 - 然后将这些结果值写入 Score 矩阵。 为此方法编写了一个新内核。 在我们研究该方法本身之后,再加以考虑。
如同先前的方法,AttentionScore 接收指向初始数据缓冲区的指针,并将获取的值记录在参数当中。 如此,在方法开始时,我们检查所收指针的有效性。
bool CNeuronMLMHAttentionOCL::AttentionScore(CBufferDouble *qkv, CBufferDouble *scores, bool mask=true) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID) return false;
遵照上述逻辑,我们来创建与 GPU 进行数据交换的缓冲区。
if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false;
准备工作完成之后,我们进入指定内核参数。 该内核的线程将在两个维度上创建:在输入序列元素的上下文中,以及关注目击者的上下文中。 这可为序列的所有元素和所有关注目击者提供并行计算。
uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionScore,def_k_mhas_score,scores.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_dimension,iWindowKey); OpenCL.SetArgument(def_k_MHAttentionScore,def_k_mhas_mask,(int)mask);
接着,我们进入进行内核调用。 计算结果在 'score' 缓冲区中读取。
if(!OpenCL.Execute(def_k_MHAttentionScore,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionScore: %d",GetLastError()); return false; } //--- return scores.BufferRead(); }
我们来查看所谓的 MHAttentionScore 内核逻辑。 如上所示,内核从参数里接收指向 qkv 源数据数组的指针,和记录结果得分的数组。 还有,内核在参数中接收内部向量的大小(Query、Key)和一个启用屏蔽后续元素算法的标志。
首先,我们获得正在处理的查询 q 的序号,和关注目击者 h。 再有,我们获得查询和关注目击者数量的维度。
__kernel void MHAttentionScore(__global double *qkv, ///<[in] Matrix of Querys, Keys, Values __global double *score, ///<[out] Matrix of Scores int dimension, ///< Dimension of Key int mask ///< 1 - calc only previous units, 0 - calc all ) { int q=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1);
根据获得的数据,判断 'query' 和 'score' 在数组中的移位。
int shift_q=dimension*(h+3*q*heads); int shift_s=units*(h+q*heads);
另外,计算分数校正系数。
double koef=sqrt((double)dimension); if(koef<1) koef=1;
关注分数是在循环里进行计算的,在其内我们将遍历相应关注目击者里整个元素序列的键值。
在循环开始时,检查使用关注机制的条件。 如果启用了此功能,则检查密钥的序列号。 如果当前键值与序列的下一个元素对应,则将零分数写入“分数”数组,然后转到下一个元素。
double sum=0; for(int k=0;k<units;k++) { if(mask>0 && k>q) { score[shift_s+k]=0; continue; }
如果计算关注分数是为所分析的键值 ,则我们组织一个嵌套循环来计算两个向量的乘积。 请注意,循环主体有两条计算分支:一条分支使用矢量计算,而另一条分支则没有这种计算。 若从 key 向量的当前位置到最后一个元素有 4 个或更多元素时,采用第一条分支;第二条分支则在 key 向量元素数量并非 4 的倍数时,处理最后的元素。
double result=0; int shift_k=dimension*(h+heads*(3*k+1)); for(int i=0;i<dimension;i++) { if((dimension-i)>4) { result+=dot((double4)(qkv[shift_q+i],qkv[shift_q+i+1],qkv[shift_q+i+2],qkv[shift_q+i+3]), (double4)(qkv[shift_k+i],qkv[shift_k+i+1],qkv[shift_k+i+2],qkv[shift_k+i+3])); i+=3; } else result+=(qkv[shift_q+i]*qkv[shift_k+i]); }
根据变换器算法,关注分数利用 SoftMax 函数进行常规化。 为了实现此功能,我们将向量乘积的结果除以校正系数,并判断结果值的指数。 计算结果应写入 “score” 张量的相应元素之中,并加到指数总和当中。
result=exp(clamp(result/koef,-30.0,30.0)); if(isnan(result)) result=0; score[shift_s+k]=result; sum+=result; }
与此类似,我们将计算所有元素的指数。 为了完成关注分数的 SoftMax 常规化,我们规划另一个循环,在其中 “Score” 张量的所有元素都除以先前算出的指数和。
for(int k=0;(k<units && sum>1);k++) score[shift_s+k]/=sum; }
在循环结束时退出内核。
我们继续利用 feedForward 方法,并研究 AttentionOut 辅助方法。 该方法从参数里接收指向三个张量指针:QKV、Scores 和 Out。 该方法的结构类似于之前研究的结构。 它在两个维度上启动 MHAttentionOut 内核:序列元素和关注目击者。
bool CNeuronMLMHAttentionOCL::AttentionOut(CBufferDouble *qkv, CBufferDouble *scores, CBufferDouble *out) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(qkv)==POINTER_INVALID || CheckPointer(scores)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) return false; uint global_work_offset[2]= {0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iHeads; if(!qkv.BufferCreate(OpenCL)) return false; if(!scores.BufferCreate(OpenCL)) return false; if(!out.BufferCreate(OpenCL)) return false; //--- OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_qkv,qkv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_score,scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MHAttentionOut,def_k_mhao_out,out.GetIndex()); OpenCL.SetArgument(def_k_MHAttentionOut,def_k_mhao_dimension,iWindowKey); if(!OpenCL.Execute(def_k_MHAttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel MHAttentionOut: %d",GetLastError()); return false; } //--- return out.BufferRead(); }
如同以前的内核一样,考虑到多目击者关注,重新编写了 MHAttentionOut。 它采用单一缓冲区来处理 queries、keys 和 values 张量。 内核从参数里接收指向张量 Score、QKV、Out 的指针,和 value 向量大小。 第一和第二个缓冲区提供原始数据,最后一个则用于记录结果。
另外,在内核开始时,判断要处理的查询 q 的序号,关注目击者 h,以及查询和关注目击者的数量维度。
__kernel void MHAttentionOut(__global double *scores, ///<[in] Matrix of Scores __global double *qkv, ///<[in] Matrix of Values __global double *out, ///<[out] Output tensor int dimension ///< Dimension of Value ) { int u=get_global_id(0); int units=get_global_size(0); int h=get_global_id(1); int heads=get_global_size(1);
接下来,判断所需关注分数的位置,以及正在分析的输出值向量第一个元素的位置。 此外,计算 QKV 张量中一个元素的向量的长度 - 该值将用于确定 QKV 张量中的偏移。
int shift_s=units*(h+heads*u); int shift_out=dimension*(h+heads*u); int layer=3*dimension*heads;
我们将针对主体计算实现嵌套循环。 外循环将以 values 向量的大小运行;内循环将按照原始序列中的元素数量执行。 在外循环开始时,我们声明一个保存计算结果数值的变量,并将其初始化为零。 内循环开始为 values 向量定义一个移位。 请注意,内循环的步长等于 4,这是因为稍后我们将使用向量计算。
for(int d=0;d<dimension;d++) { double result=0; for(int v=0;v<units;v+=4) { int shift_v=dimension*(h+heads*(3*v+2))+d;
如同在 MHAttentionScore 内核中一样,我们将计算分为两个线程:一个采用向量计算,而
另一个则没有它们。 第二个线程仅当序列长度并非 4 的倍数,处理最后的元素。
if((units-v)>4) { result+=dot((double4)(scores[shift_s+v],scores[shift_s+v+1],scores[shift_s+v+1],scores[shift_s+v+3]), (double4)(qkv[shift_v],qkv[shift_v+layer],qkv[shift_v+2*layer],qkv[shift_v+3*layer])); } else for(int l=0;l<(int)fmin((double)(units-v),4.0);l++) result+=scores[shift_s+v+l]*qkv[shift_v+l*layer]; } out[shift_out+d]=result; } }
退出嵌套循环后,将结果值写入输出张量的相应元素。
进而,在 feedForward 方法中,调用上述的 ConvolutionForward 方法。 附件中提供了所有方法和函数的完整代码。
与所有之前研究过的类一样,后馈过程包含两个子过程:传播误差梯度和更新权重。 在 calcInputGradients 里已经实现了第一部分。 在 updateInputWeights 中则实现了第二部分。
calcInputGradients 方法的构造与 feedForward 类似。 该方法从参数里接收指向神经网络上一层的指针,这是为了传递误差梯度。 因此,在方法开始时,需检查所收到指针的有效性。
bool CNeuronMLMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
然后,我们锁定从神经元下一层接收到的梯度张量,并规划一个循环遍历所有内层,依次计算误差梯度。 由于这是反馈过程,因此循环将以相反的顺序遍历内层。
for(int i=(int)iLayers-1; (i>=0 && !IsStopped()); i--) { //--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2),out_grad,FF_Tensors.At(i*6+1),FF_Tensors.At(i*6+4),4*iWindow,iWindow,None)) return false; CBufferDouble *temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(i*6+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+3); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(i*6+4),FF_Tensors.At(i*6),temp,iWindow,4*iWindow,LReLU)) return false;
在循环开始时,计算由变换器前馈模块的神经元的完全连接层传播过来的误差梯度。 该迭代由 ConvolutionInputGradients 方法执行。 方法完成后释放缓冲区。
由于我们的算法实现了数据流贯穿整个过程,因此应该对误差梯度实现相同的过程。 如此,把从前馈模块获得的误差梯度,与从前一层神经元接收到的误差梯度相加。 为了消除“崩溃梯度”的风险,需把两个向量的总和进行常规化。 所有这些操作都是在 SumAndNormilize 方法中执行的。 方法完成后释放缓冲区。
//--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; if(i!=(int)iLayers-1) out_grad.BufferFree(); out_grad=temp; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(i*6+4); temp.BufferFree(); temp=FF_Tensors.At(i*6); temp.BufferFree();
进而在算法当中,我们将误差梯度除以关注目击者。 这是调用调用 ConvolutionInputGradients方法处理 W0 矩阵来完成的。
//--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i*(optimization==SGD ? 6 : 9)),out_grad,AO_Tensors.At(i*2),AO_Tensors.At(i*2+1),iWindowKey*iHeads,iWindow,None)) return false; temp=FF_Weights.At(i*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=AO_Tensors.At(i*2); temp.BufferFree();
进而在 AttentionInsideGradients 方法中,规划沿关注目击者的梯度传播。
if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i*2),QKV_Tensors.At(i*2+1),S_Tensors.At(i*2),S_Tensors.At(i*2+1),AO_Tensors.At(i*2+1))) return false; temp=QKV_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2); temp.BufferFree(); temp=S_Tensors.At(i*2+1); temp.BufferFree(); temp=AO_Tensors.At(i*2+1); temp.BufferFree();
在循环的末尾,我们计算传递到上一层的误差梯度。 在此,从前一次迭代接收到的误差梯度将通过级联张量 QKV_Weights 传递,然后将接收到的向量与从自关注机制前馈模块而来的误差梯度求和,并对结果进行常规化,以便消除崩溃梯度。
CBufferDouble *inp=NULL; if(i==0) { inp=prevLayer.getOutput(); temp=prevLayer.getGradient(); } else { temp=FF_Tensors.At(i*6-1); inp=FF_Tensors.At(i*6-4); } if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(i*2+1),inp,temp,iWindow,3*iWindowKey*iHeads,None)) return false; //--- Sum and normalize gradients if(IsStopped() || !SumAndNormilize(out_grad,temp,temp)) return false; out_grad.BufferFree(); if(i>0) out_grad=temp; temp=QKV_Weights.At(i*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(i*2+1); temp.BufferFree(); } //--- return true; }
不要忘记释放占用的数据缓冲区。 请注意,前一层的数据缓冲区保留在 GPU 内存中。
我们来看一下被调用的方法。 如您所见,调用频率最高的方法是 ConvolutionInputGradients,它基于卷积层的类似方法,并且针对当前任务进行了优化。 该方法从参数里接收指向权重张量、下一层梯度、上一层输出数据和张量的指针,以便存储迭代结果。 同样,该方法从参数里接收输入和输出数据窗口的大小,以及所采用的激活函数。
bool CNeuronMLMHAttentionOCL::ConvolutionInputGradients(CBufferDouble *weights, CBufferDouble *gradient, CBufferDouble *inputs, CBufferDouble *inp_gradient, uint window, uint window_out, uint activ) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(weights)==POINTER_INVALID || CheckPointer(gradient)==POINTER_INVALID || CheckPointer(inputs)==POINTER_INVALID || CheckPointer(inp_gradient)==POINTER_INVALID) return false;
在方法伊始,检查所接收指针的有效性,并在 GPU 内存中创建数据缓冲区。
if(!weights.BufferCreate(OpenCL)) return false; if(!gradient.BufferCreate(OpenCL)) return false; if(!inputs.BufferCreate(OpenCL)) return false; if(!inp_gradient.BufferCreate(OpenCL)) return false;
创建数据缓冲区之后,实现相应的 OpenCL 程序内核调用。 在此,我们所采用的卷积网络内核并无变化。
//--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=inputs.Total(); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_w,weights.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_g,gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_o,inputs.GetIndex()); OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv,def_k_chgc_matrix_ig,inp_gradient.GetIndex()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_outputs,gradient.Total()); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_step,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_in,window); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_window_out,window_out); OpenCL.SetArgument(def_k_CalcHiddenGradientConv,def_k_chgc_activation,activ); //Comment(com+"\n "+(string)__LINE__+"-"__FUNCTION__); if(!OpenCL.Execute(def_k_CalcHiddenGradientConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel CalcHiddenGradientConv: %d",GetLastError()); return false; } //--- return inp_gradient.BufferRead(); }
AttentionInsideGradients方法还会从 ConvolutionInputGradients 方法里调用,其构造根据类似的算法。 请参阅附件中的方法代码。 现在,我们看一下从指定方法调用的 OpenCL 程序内核,因为所有计算都是在内核中执行。
MHAttentionInsideGradients 内核是由线程在两个维度上启动的:序列元素和关注目击者。 内核从参数里接收指向级联 QKV 张量及其梯度的张量、Scores 矩阵张量及其梯度、前一次迭代的误差梯度张量以及键向量的大小的指针。
__kernel void MHAttentionInsideGradients(__global double *qkv,__global double *qkv_g, __global double *scores,__global double *scores_g, __global double *gradient, int dimension) { int u=get_global_id(0); int h=get_global_id(1); int units=get_global_size(0); int heads=get_global_size(1); double koef=sqrt((double)dimension); if(koef<1) koef=1;
在方法开始时,我们获得处理后的序列元素和注意头的序号,以及它们的大小。 另外,我们计算 Scores 矩阵,并更新系数。
然后,我们规划一个循环来计算 Scores 矩阵的误差梯度。 在循环之后设置屏障,我们可以跨线程同步所有计算过程。 仅在Scores 矩阵的梯度完全重新计算之后,算法才会切换到下一个运算模块。
//--- Calculating score's gradients uint shift_s=units*(h+u*heads); for(int v=0;v<units;v++) { double s=scores[shift_s+v]; if(s>0) { double sg=0; int shift_v=dimension*(h+heads*(3*v+2)); int shift_g=dimension*(h+heads*v); for(int d=0;d<dimension;d++) sg+=qkv[shift_v+d]*gradient[shift_g+d]; scores_g[shift_s+v]=sg*(s<1 ? s*(1-s) : 1)/koef; } else scores_g[shift_s+v]=0; } barrier(CLK_GLOBAL_MEM_FENCE);
我们来实现另一个循环,以便计算 queries、key 和 value 向量的误差梯度。
//--- Calculating gradients for Query, Key and Value uint shift_qg=dimension*(h+3*u*heads); uint shift_kg=dimension*(h+(3*u+1)*heads); uint shift_vg=dimension*(h+(3*u+2)*heads); for(int d=0;d<dimension;d++) { double vg=0; double qg=0; double kg=0; for(int l=0;l<units;l++) { uint shift_q=dimension*(h+3*l*heads)+d; uint shift_k=dimension*(h+(3*l+1)*heads)+d; uint shift_g=dimension*(h+heads*l)+d; double sg=scores_g[shift_s+l]; kg+=sg*qkv[shift_q]; qg+=sg*qkv[shift_k]; vg+=gradient[shift_g]*scores[shift_s+l]; } qkv_g[shift_qg+d]=qg; qkv_g[shift_kg+d]=kg; qkv_g[shift_vg+d]=vg; } }
附件中提供了所有方法和函数的完整代码。
权重在 updateInputWeights 方法中更新,其依据先前研究的 feedForward 和 calcInputGradients 方法的原理构建。 在此方法中,仅顺序调用了一个更新卷积网络权重的 ConvolutuionUpdateWeights 辅助方法。
bool CNeuronMLMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL)==POINTER_INVALID) return false; CBufferDouble *inputs=NeuronOCL.getOutput(); for(uint l=0; l<iLayers; l++) { if(IsStopped() || !ConvolutuionUpdateWeights(QKV_Weights.At(l*(optimization==SGD ? 2 : 3)),QKV_Tensors.At(l*2+1),inputs,(optimization==SGD ? QKV_Weights.At(l*2+1) : QKV_Weights.At(l*3+1)),(optimization==SGD ? NULL : QKV_Weights.At(l*3+2)),iWindow,3*iWindowKey*iHeads)) return false; if(l>0) inputs.BufferFree(); CBufferDouble *temp=QKV_Weights.At(l*(optimization==SGD ? 2 : 3)); temp.BufferFree(); temp=QKV_Tensors.At(l*2+1); temp.BufferFree(); if(optimization==SGD) { temp=QKV_Weights.At(l*2+1); } else { temp=QKV_Weights.At(l*3+1); temp.BufferFree(); temp=QKV_Weights.At(l*3+2); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)),FF_Tensors.At(l*6+3),AO_Tensors.At(l*2),(optimization==SGD ? FF_Weights.At(l*6+3) : FF_Weights.At(l*9+3)),(optimization==SGD ? NULL : FF_Weights.At(l*9+6)),iWindowKey*iHeads,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)); temp.BufferFree(); temp=FF_Tensors.At(l*6+3); temp.BufferFree(); temp=AO_Tensors.At(l*2); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+3); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+3); temp.BufferFree(); temp=FF_Weights.At(l*9+6); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1),FF_Tensors.At(l*6+4),FF_Tensors.At(l*6),(optimization==SGD ? FF_Weights.At(l*6+4) : FF_Weights.At(l*9+4)),(optimization==SGD ? NULL : FF_Weights.At(l*9+7)),iWindow,4*iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+1); temp.BufferFree(); temp=FF_Tensors.At(l*6+4); temp.BufferFree(); temp=FF_Tensors.At(l*6); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+4); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+4); temp.BufferFree(); temp=FF_Weights.At(l*9+7); temp.BufferFree(); } //--- if(IsStopped() || !ConvolutuionUpdateWeights(FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2),FF_Tensors.At(l*6+5),FF_Tensors.At(l*6+1),(optimization==SGD ? FF_Weights.At(l*6+5) : FF_Weights.At(l*9+5)),(optimization==SGD ? NULL : FF_Weights.At(l*9+8)),4*iWindow,iWindow)) return false; temp=FF_Weights.At(l*(optimization==SGD ? 6 : 9)+2); temp.BufferFree(); temp=FF_Tensors.At(l*6+5); if(temp!=Gradient) temp.BufferFree(); temp=FF_Tensors.At(l*6+1); temp.BufferFree(); if(optimization==SGD) { temp=FF_Weights.At(l*6+5); temp.BufferFree(); } else { temp=FF_Weights.At(l*9+5); temp.BufferFree(); temp=FF_Weights.At(l*9+8); temp.BufferFree(); } inputs=FF_Tensors.At(l*6+2); } //--- return true; }
附件中提供了所有类及其方法的完整代码。
与之前所有文章一样,我们在创建新类之后应对基类进行修改,以便确保网络能正常运行。
我们来添加一个新的类标识符。
#define defNeuronMLMHAttentionOCL 0x7889 ///<Multilayer multi-headed attention neuron OpenCL \details Identified class #CNeuronMLMHAttentionOCL
同样,在定义模块中,我们添加处理 OpenCL 程序新内核的常量。
#define def_k_MHAttentionScore 20 ///< Index of the kernel of the multi-heads attention neuron to calculate score matrix (#MHAttentionScore) #define def_k_mhas_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhas_score 1 ///< Matrix of Scores #define def_k_mhas_dimension 2 ///< Dimension of Key #define def_k_mhas_mask 3 ///< 1 - calc only previous units, 0 - calc all //--- #define def_k_MHAttentionOut 21 ///< Index of the kernel of the multi-heads attention neuron to calculate multi-heads out matrix (#MHAttentionOut) #define def_k_mhao_score 0 ///< Matrix of Scores #define def_k_mhao_qkv 1 ///< Matrix of Queries, Keys, Values #define def_k_mhao_out 2 ///< Matrix of Outputs #define def_k_mhao_dimension 3 ///< Dimension of Key //--- #define def_k_MHAttentionGradients 22 ///< Index of the kernel for gradients calculation process (#AttentionInsideGradients) #define def_k_mhag_qkv 0 ///< Matrix of Queries, Keys, Values #define def_k_mhag_qkv_g 1 ///< Matrix of Gradients to Queries, Keys, Values #define def_k_mhag_score 2 ///< Matrix of Scores #define def_k_mhag_score_g 3 ///< Matrix of Scores Gradients #define def_k_mhag_gradient 4 ///< Matrix of Gradients from previous iteration #define def_k_mhag_dimension 5 ///< Dimension of Key
还有,我们在神经网络类构造函数中添加新内核的声明。
//--- create kernels opencl.SetKernelsCount(23); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers"); opencl.KernelCreate(def_k_MHAttentionGradients,"MHAttentionInsideGradients"); opencl.KernelCreate(def_k_MHAttentionScore,"MHAttentionScore"); opencl.KernelCreate(def_k_MHAttentionOut,"MHAttentionOut");
并在神经网络构造函数中创建一种新型的神经元。
case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl=new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_mlattention_ocl.Init(outputs,0,opencl,desc.window,desc.window_out,desc.step,desc.count,desc.layers,desc.optimization)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; delete temp; return; } neuron_mlattention_ocl=NULL; break;
我们还要将新的神经元类的处理添加到 CNeuronBaseOCL 神经元基类的调度方法之中。
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronMLMHAttentionOCL *mlat=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; case defNeuronMLMHAttentionOCL: mlat=TargetObject; temp=GetPointer(this); return mlat.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
附件中提供了所有类及其方法的完整代码。
已经创建了两个智能交易系统来测试新架构:Fractal_OCL_AttentionMLMH 和 Fractal_OCL_AttentionMLMH_v2。 这些 EA 是基于上一篇文章的 EA 创建的,仅替换了关注区域。 Fractal_OCL_AttentionMLMH EA 有一个 5 层模块,带有 8 个自关注目击者。 第二个 EA 使用一个 12 层模块,带有 12 个自关注目击者。
在同一数据集上测试了新的神经网络类,该数据集在之前的测试中曾经用过:神经网络馈入 EURUSD,时间帧为 H1,最后 20 根烛条的历史数据。
测试结果证实了这个假设,即更多的参数需要更长的训练时间。 在第一个训练迭代,参数较少的智能交易系统展现出的结果更稳定。 然而,随着训练时间的延申,带有大量参数的智能交易系统会展现出更佳的数值。 通常,在 33 个迭代之后,Fractal_OCL_AttentionMLMH_v2 的误差降低到 Fractal_OCL_AttentionMLMH EA 的误差水平以下,且它会进一步保持低水平。
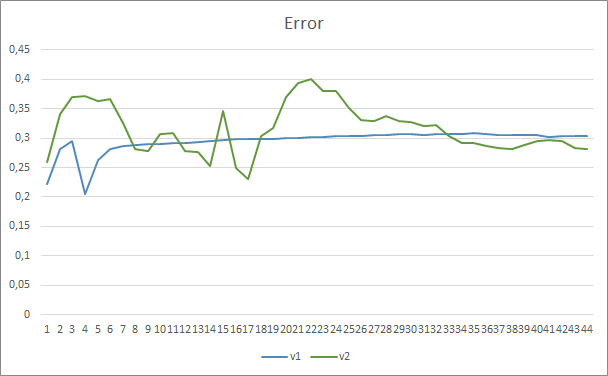
遗漏的形态参数显示了相似的结果。 在训练开始时,Fractal_OCL_AttentionMLMH_v2 EA 的非平衡参数遗漏了超过 50% 的形态。 但随着训练持续,该值逐渐下降,经过 27 个迭代之后,稳定在 3-5%,而参数较少的 EA 表现出更平滑的结果,但同时却遗漏了 10-16% 的形态。
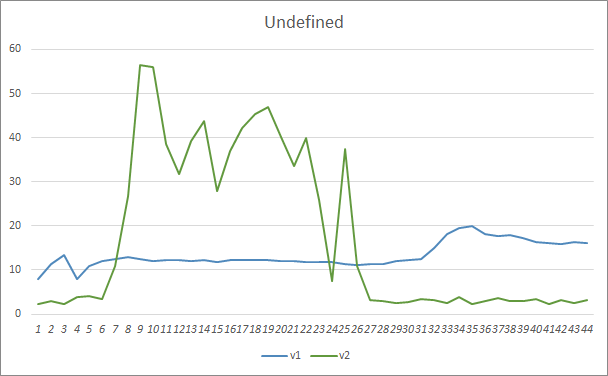
在形态预测准确性方面,两款智能交易系统均展现出均等的结果,为 22-23%。
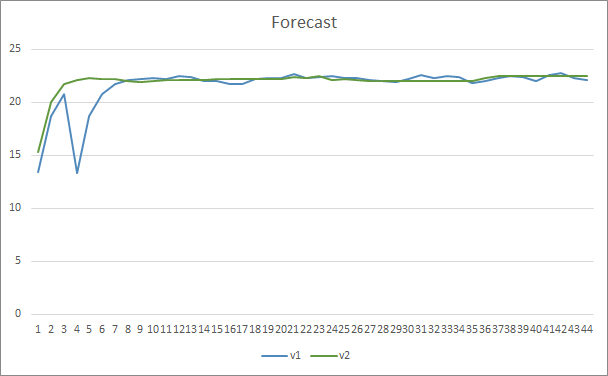
在本文中,我们创建了一个新的关注神经元类,与 OpenAI 提出的 GPT 体系结构类似。 当然,不可能以完整的形式重复和训练这些架构,因为它们的训练和操作会占用大量时间和资源。 不过,若出于在神经网络中创建交易机器人的目的,我们所创建的对象能出色工作。
…
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH.mq5 | 智能交易系统 | 采用 GTP 架构的分类神经网络(输出层中有 3 个神经元)和 5 个关注层的智能交易系统 |
| 2 | Fractal_OCL_AttentionMLMH_v2.mq5 | 智能交易系统 | 采用 GTP 架构的分类神经网络(输出层中有 3 个神经元)和 12 个关注层的智能交易系统 |
| 3 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 4 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
| 5 | NN.chm | HTML 帮助 | 经编译的 CHM 文件。 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...