在之前的文章中,我们采用了不同类型的神经元,但我们始终利用随机梯度下降法来训练神经网络。 该方法可称为基本方法,在实践中经常会用到其变体。 不过,还有许多其他的神经网络训练方法。 今天,我提议研究自适应学习方法。 这一族方法可在神经网络训练期间改变神经元学习速率。
您知道并非所有馈入神经网络的特征值都会对最终结果产生相同的影响。 一些参数可能会包含很多噪声,且比其他变化更频繁,振幅也有所不同。 其他参数的样本可能包含稀有值,当采用固定学习速率训练神经网络时,这些稀有值可能不会被注意到。 之前研究过的随机梯度下降方法的缺点之一是在此类样本上无法使用优化机制。 结果就是,学习过程可能在局部最小值处停止。 可采用自适应方法训练神经网络来解决该问题。 这些方法能够在神经网络训练过程中动态改变学习率。 这样的方法及其变体有很多数量。 我们来研究其中最受欢迎的。
自适应梯度法于 2011 年提出。 它是随机梯度下降法的一种变体。 经由比较这些方法的数学公式,我们轻易注意到一个不同之处:对于所有之前的训练迭代,AdaGrad 的学习率除以梯度平方和的平方根。 这种方式可降低频繁更新参数的学习率。
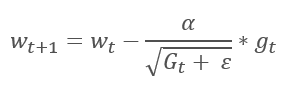
而该方法的主要缺点来自其公式:梯度的平方和只能增长,因此学习率趋于 0。 这最终会导致训练停止。
利用这种方法需要额外的计算和内存分配,以便保存每个神经元的梯度平方和。
AdaGrad 方法的逻辑延续自 RMSProp 方法。 为了避免学习率跌落到 0,在更新权重的公式分母中,已用梯度平方的指数均值替换过去的梯度平方和。 这种方法消除了分母中数值的恒定无限增长。 甚而,它更加关注表征模型当前状态的最新梯度值。
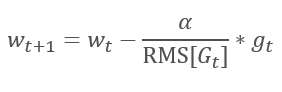
Adadelta 自适应方法几乎与 RMSProp 同时提出。 此方法类似,它在更新权重的公式分母中采用了平方梯度总和的指数均值。 但与 RMSProp 不同,此方法彻底拒绝更新公式中的学习率,并在所分析参数中用之前修改的平方和的指数均值来替代。
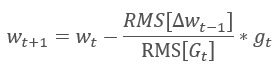
这种方式能够从更新权重的公式中删除学习率,并创建高度自适应的学习算法。 然而,此方法需要额外的计算迭代,并为存储每个神经元的额外值而分配内存。
2014 年,Diederik P.Kingma 和 Jimmy Lei Ba 提出了自适应动量评估方法(Adam)。 根据作者的说法,该方法结合了 AdaGrad 和 RMSProp 方法的优点,非常适合在线训练。 该方法在不同样本上始终展现出良好的结果。 在各种软件包中,通常建议按照默认使用它。
该方法基于计算出的梯度 m 的指数平均值,和平方梯度 v 的指数平均值。 每个指数平均值都有其自己的超参数 ß,由它判定平均周期。
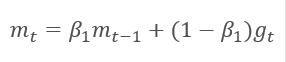
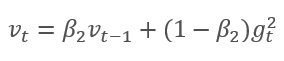
作者建议默认采用 ß1 0.9 和 ß2 0.999。 在此情况下,m0 和 v0 取零值。 采用这些参数,上面介绍的公式在训练开始时返回值接近 0,因此开始时的学习率会很低。 为了加快学习过程,作者建议修改所获得的动量。
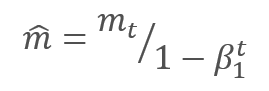
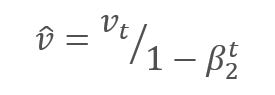
通过调整校正梯度动量 m 与平方梯度 v 的校正动量的平方根之间的比率来更新参数。 为避免除零,在分母里加入接近 0 的常数 Ɛ。 依据学习因子 α 调整所得比率,学习因子 α 在这种情况下是学习步幅的上限。 作者建议默认采用 α 0.001。
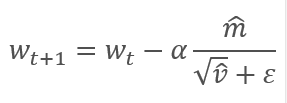
研究过理论方面之后,我们便可以进行实际实现了。 我建议采用作者提供的默认超参数来实现 Adam 方法。 进而,您可以尝试其他超参数变体。
早前建立的神经网络采用随机梯度下降法进行训练,为此我们已经实现了反向传播算法。 现有的反向传播功能可用来实现 Adam 方法。 我们只需要实现权重更新算法。 这个功能需经由 updateInputWeights 方法,它是在每个神经元类里实现的。 当然,我们不会删除之前创建的随机梯度下降算法。 我们来创建一个替代算法,令您可以选择要采用的训练方法。
研究 CNeuronBaseOCL 类的 Adam 方法实现。 首先,创建 UpdateWeightsAdam 内核实现 OpenCL 方法。 指向以下矩阵的指针则会通过参数传递给内核:
__kernel void UpdateWeightsAdam(__global double *matrix_w, __global double *matrix_g, __global double *matrix_i, __global double *matrix_m, __global double *matrix_v, int inputs, double l, double b1, double b2)
另外,在内核参数中,传递输入数据数组的大小和 Adam 算法的超参数。
在内核伊始,获取在两维的流序列号,其分别指示当前层和先前层的神经元数量。 使用接收到的编号,判断缓冲区中已处理元素的初始编号。 请注意,第二维中的结果流编号应乘以 “4”。 这是因为为了减少流数量和程序执行的总时间,我们将利用含有 4 个元素的向量计算。
{
int i=get_global_id(0);
int j=get_global_id(1);
int wi=i*(inputs+1)+j*4;
判断已处理元素在数据缓冲区中的位置后,声明矢量变量,并用相应的数值填充它们。 利用先前讲述的方法,并在向量中将缺失数据填充零值。
double4 m, v, weight, inp; switch(inputs-j*4) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[wi],0,0,0); m=(double4)(matrix_m[wi],0,0,0); v=(double4)(matrix_v[wi],0,0,0); break; case 1: inp=(double4)(matrix_i[j],1,0,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0); m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0); v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0); break; case 2: inp=(double4)(matrix_i[j],matrix_i[j+1],1,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0); break; case 3: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; default: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; }
梯度向量是通过将当前神经元的梯度乘以输入数据向量而获得的。
double4 g=matrix_g[i]*inp;
接下来,计算梯度和平方梯度的指数平均值。
double4 mt=b1*m+(1-b1)*g; double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;
计算参数变化增量。
double4 delta=l*mt/sqrt(vt);
请注意,我们尚未调整内核中的接收动量。 在此有意省略了此步骤。 因为 ß1和 ß2 对于所有神经元和 t 都是相同的,其在这里是 神经元参数更新的迭代次数,对于所有神经元也相同,然后对于所有神经元校正因子也将相同。 这就是为什么我们不会重新计算每个神经元的因子,而是在主程序代码中对其进行一次性计算,并将其传递给内核,以便依据该值调整后续的学习系数的原因。
在增量计算完成之后,我们只需要调整权重系数,并更新缓冲区中已计算的动量即可。 然后退出内核。
switch(inputs-j*4) { case 2: matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; case 1: matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; case 0: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; break; default: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; matrix_w[wi+3]+=delta.s3; matrix_m[wi+3]=mt.s3; matrix_v[wi+3]=vt.s3; break; } };
此代码还有另一个技巧。 请注意 switch 运算符中 case 情况的相反顺序。 此外, break 操作符仅在 case 0 和 default 情况之后使用。 这种方式可避免所有变体重复相同的代码。
构建内核之后,我们需要对主程序代码进行修改。 首先,在 “define” 模块里添加操控内核的常量。
#define def_k_UpdateWeightsAdam 4 #define def_k_uwa_matrix_w 0 #define def_k_uwa_matrix_g 1 #define def_k_uwa_matrix_i 2 #define def_k_uwa_matrix_m 3 #define def_k_uwa_matrix_v 4 #define def_k_uwa_inputs 5 #define def_k_uwa_l 6 #define def_k_uwa_b1 7 #define def_k_uwa_b2 8
创建指示训练方法的枚举,并在枚举中添加动量缓冲区。
enum ENUM_OPTIMIZATION { SGD, ADAM }; //--- enum ENUM_BUFFERS { WEIGHTS, DELTA_WEIGHTS, OUTPUT, GRADIENT, FIRST_MOMENTUM, SECOND_MOMENTUM };
然后,在 CNeuronBaseOCL 类主体中,添加缓冲区,用来存储动量、指数平均常数、训练迭代计数器,以及保存训练方法的变量。
class CNeuronBaseOCL : public CObject { protected: ......... ......... .......... CBufferDouble *FirstMomentum; CBufferDouble *SecondMomentum; //--- ......... ......... const double b1; const double b2; int t; //--- ......... ......... ENUM_OPTIMIZATION optimization;
在类构造函数中,设置常量的值,并初始化缓冲区。
CNeuronBaseOCL::CNeuronBaseOCL(void) : alpha(momentum), activation(TANH), optimization(SGD), b1(0.9), b2(0.999), t(1) { OpenCL=NULL; Output=new CBufferDouble(); PrevOutput=new CBufferDouble(); Weights=new CBufferDouble(); DeltaWeights=new CBufferDouble(); Gradient=new CBufferDouble(); FirstMomentum=new CBufferDouble(); SecondMomentum=new CBufferDouble(); }
不要忘记在类的析构函数中加入删除缓冲区对象的代码。
CNeuronBaseOCL::~CNeuronBaseOCL(void) { if(CheckPointer(Output)!=POINTER_INVALID) delete Output; if(CheckPointer(PrevOutput)!=POINTER_INVALID) delete PrevOutput; if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; if(CheckPointer(Gradient)!=POINTER_INVALID) delete Gradient; if(CheckPointer(FirstMomentum)!=POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)!=POINTER_INVALID) delete SecondMomentum; OpenCL=NULL; }
在类初始化函数的参数中,添加训练方法,并根据指定的训练方法来初始化缓冲区。 如果采用随机梯度下降法进行训练,初始化增量缓冲区,并删除动量缓冲区。 如果采用 Adam 方法,初始化动量缓冲区,并删除增量缓冲区。
bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type) { if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0) return false; OpenCL=open_cl; optimization=optimization_type; //--- .................... .................... .................... .................... //--- if(numOutputs>0) { if(CheckPointer(Weights)==POINTER_INVALID) { Weights=new CBufferDouble(); if(CheckPointer(Weights)==POINTER_INVALID) return false; } int count=(int)((numNeurons+1)*numOutputs); if(!Weights.Reserve(count)) return false; for(int i=0;i<count;i++) { double weigh=(MathRand()+1)/32768.0-0.5; if(weigh==0) weigh=0.001; if(!Weights.Add(weigh)) return false; } if(!Weights.BufferCreate(OpenCL)) return false; //--- if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID) { DeltaWeights=new CBufferDouble(); if(CheckPointer(DeltaWeights)==POINTER_INVALID) return false; } if(!DeltaWeights.BufferInit(count,0)) return false; if(!DeltaWeights.BufferCreate(OpenCL)) return false; if(CheckPointer(FirstMomentum)==POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)==POINTER_INVALID) delete SecondMomentum; } else { if(CheckPointer(DeltaWeights)==POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum)==POINTER_INVALID) { FirstMomentum=new CBufferDouble(); if(CheckPointer(FirstMomentum)==POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count,0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum)==POINTER_INVALID) { SecondMomentum=new CBufferDouble(); if(CheckPointer(SecondMomentum)==POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count,0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; } } else { if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; } //--- return true; }
另外,修改权重更新方法 updateInputWeights。 首先,根据训练方法创建分支算法。
bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=Neurons(); global_work_size[1]=NeuronOCL.Neurons(); if(optimization==SGD) {
对于随机梯度下降法,按原样调用整个代码。
OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha); ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError()); return false; } }
在 Adam 方法分支中,为相应的内核设置数据交换缓冲区。
else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex())) return false;
然后调整当前训练迭代的学习率。
double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
设置训练超参数。
if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons())) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2)) return false;
由于我们在内核中采用矢量值进行计算,因此将第二维的线程数减少了四倍。
uint rest=global_work_size[1]%4; global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);
准备工作完成后,调用内核,并增加训练迭代计数器。
ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError()); return false; } t++; }
分支后,无论采用哪种训练方法,均应读取重新计算的权重。 正如我在上一篇文章中解释的那样,还必须为隐藏层读取缓冲区,因为此操作不仅读取数据,且还会开启内核执行。
//--- return NeuronOCL.Weights.BufferRead(); }
除了训练方法计算的算法之外,还需要调整存储和加载有关先前神经元训练结果信息的方法。 在 Save 方法中,实现训练方法的保存,并添加训练迭代计数器。
bool CNeuronBaseOCL::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; if(FileWriteInteger(file_handle,Type())<INT_VALUE) return false; //--- if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE) return false;
保存的缓冲区方法两种训练方法通用,并未改变。
if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle)) return false; if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle)) return false; if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle)) return false; //--- if(CheckPointer(Weights)==POINTER_INVALID) { FileWriteInteger(file_handle,0); return true; } else FileWriteInteger(file_handle,1); //--- if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle)) return false;
之后,分别为每种训练方法创建分支算法,同时保存特定的缓冲区。
if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle)) return false; } else { if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle)) return false; if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle)) return false; } //--- return true; }
在 Load 方法中以相同的顺序进行类似的修改。
附件中提供了所有方法和函数的完整代码。
为了令所有类都保持相同的操作条件,在类中进行类似修改,以纯 MQL5 进行操作,不使用 OpenCL。
首先,在 CConnection 类里添加存储动量数据的变量,并在类构造函数中设置初始值。
class CConnection : public CObject { public: double weight; double deltaWeight; double mt; double vt; CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }
还必须将新变量的处理添加到保存和加载连接数据的方法当中。
bool CConnection::Save(int file_handle) { ........... ........... ........... if(FileWriteDouble(file_handle,mt)<=0) return false; if(FileWriteDouble(file_handle,vt)<=0) return false; //--- return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CConnection::Load(int file_handle) { ............ ............ ............ mt=FileReadDouble(file_handle); vt=FileReadDouble(file_handle); //--- return true; }
下一步,在 CNeuronBase 神经元类里添加存储优化方法和权重更新迭代计数器的变量。
class CNeuronBase : public CObject { protected: ......... ......... ......... ENUM_OPTIMIZATION optimization; const double b1; const double b2; int t;
然后,神经元初始化方法也需要修改。 在方法的参数中添加一个指示优化方法的变量,并将其保存在上面定义的变量之中。
bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type) { optimization=optimization_type;
之后,我们根据优化方法创建算法分支,并将其添加到 updateInputWeights 方法当中。 在遍历连接之前,重新计算调整后的学习率,并在循环中创建两个计算权重的分支。
bool CNeuron::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t)); int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); CConnection *con=neuron.Connections.At(m_myIndex); if(CheckPointer(con)==POINTER_INVALID) continue; if(optimization==SGD) con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); else { con.mt=b1*con.mt+(1-b1)*gradient; con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001; con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt); t++; } } //--- return true; }
在保存和加载方法里添加新变量的处理逻辑。
下面的附件中提供了所有方法的完整代码。
除在神经元类里进行修改之外,还需要在我们的代码中修改其他对象。 首先,我们需要将有关训练方法的信息从主程序传递到神经元。 来自主程序的数据经由 CLayerDescription 类传递给神经网络类。 应向该类里添加相应的方法,从而传递有关训练方法的信息。
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
现在,针对 CNet 神经网络类的构造函数做最后的补充。 在初始化网络神经元之处添加一个优化方法的指示,OpenCL 内核的使用次数递增,并声明一个新的优化内核 - Adam。 以下是修改后的构造函数代码,其中以高亮标记的是修改部分。
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
//---
CLayer *temp;
CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
CNeuronBase *neuron=NULL;
CNeuronProof *neuron_p=NULL;
int output_count=0;
int temp_count=0;
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
CNeuronBaseOCL *neuron_ocl=NULL;
switch(desc.type)
{
case defNeuron:
case defNeuronBaseOCL:
neuron_ocl=new CNeuronBaseOCL();
if(CheckPointer(neuron_ocl)==POINTER_INVALID)
{
delete temp;
return;
}
if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
{
delete temp;
return;
}
neuron_ocl.SetActivationFunction(desc.activation);
if(!temp.Add(neuron_ocl))
{
delete neuron_ocl;
delete temp;
return;
}
neuron_ocl=NULL;
break;
default:
return;
break;
}
}
else
for(int n=0; n<neurons; n++)
{
switch(desc.type)
{
case defNeuron:
neuron=new CNeuron();
if(CheckPointer(neuron)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
neuron.Init(outputs,n,desc.optimization);
neuron.SetActivationFunction(desc.activation);
break;
case defNeuronConv:
neuron_p=new CNeuronConv();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronProof:
neuron_p=new CNeuronProof();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronLSTM:
neuron_p=new CNeuronLSTM();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
output_count=(next!=NULL ? next.window : desc.step);
if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
neuron=neuron_p;
break;
}
if(!temp.Add(neuron))
{
delete temp;
delete layers;
return;
}
neuron=NULL;
}
if(!layers.Add(temp))
{
delete temp;
delete layers;
return;
}
}
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(5);
opencl.KernelCreate(def_k_FeedForward,"FeedForward");
opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
return;
}
附件中提供了所有类及其方法的完整代码。
经由 Adam 方法进行的优化测试,其所依据条件与早期测试中使用的相同:品种 EURUSD,时间帧 H1,20 根连续烛条的数据馈入网络,并根据最近两年的历史进行训练。 已为测试创建了 Fractal_OCL_Adam 智能交易系统。 该智能交易系统的创建,则是基于 Fractal_OCL EA,在主程序的 OnInit 函数中描述神经网络时,指定 Adam 优化方法。
desc.count=(int)HistoryBars*12; desc.type=defNeuron; desc.optimization=ADAM;
层和神经元的数量没有变化。
智能交易系统初始化时的随机权重为 -1 到 1,不包括零值。 在测试期间,在第二个训练迭代之后,神经网络误差稳定在 30% 左右。 您可能还记得,采用随机梯度下降法学习时,在第 5 个训练迭代之后,误差稳定在 42% 左右。
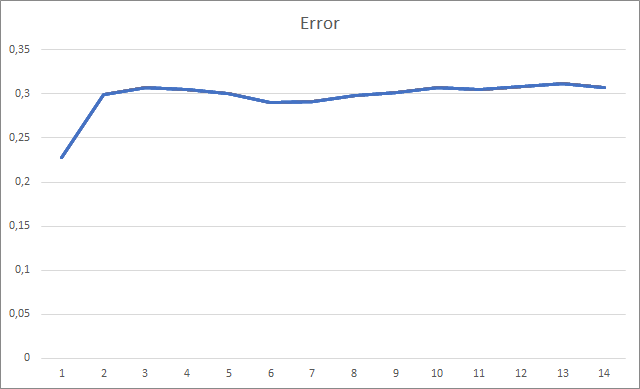
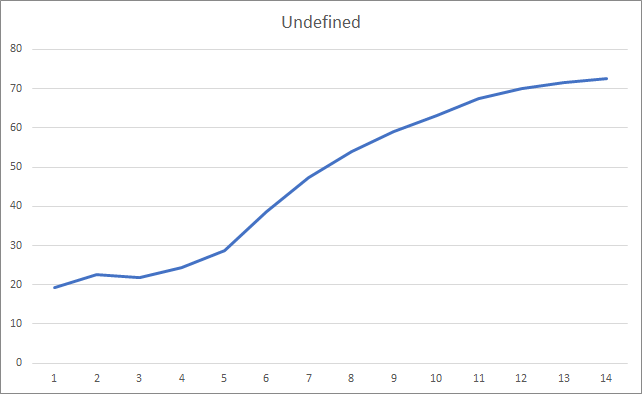
缺失的分形图形展示出数值递增贯穿于整个训练过程。 不过,经过 12 个训练迭代之后,数值递增率逐渐降低。 第 14 个迭代后,该值等于 72.5%。 当训练相似的神经网络时采用随机梯度下降方法,则在不同学习率的情况下,经过 10 个迭代后分形缺失率为 97-100%。
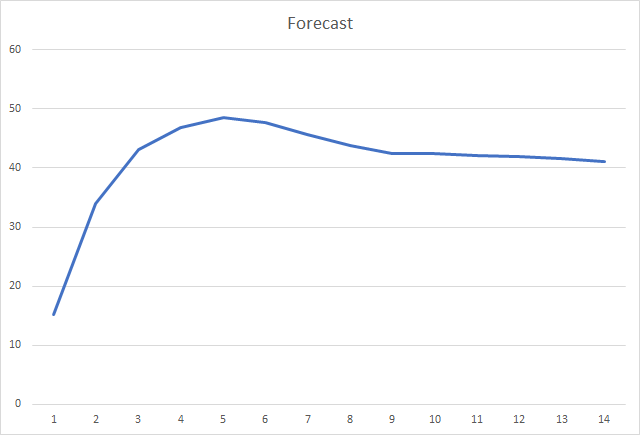
而且,最重要的指标可能是正确定义的分形的百分比。 第五次学习迭代后,该值达到 48.6%,然后逐渐下降到 41.1%。 采用随机梯度下降法时,在 90 个迭代之后该值不超过 10%。
本文研究优化神经网络参数的自适应方法。 我们已将 Adam 优化方法添加到先前创建的神经网络模型当中。 在测试过程中,采用 Adam 方法训练神经网络。 当采用随机梯度下降法训练相似的神经网络时,结果超过了之前得到的结果。
完成的工作表明我们正朝着目标前进。
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Fractal_OCL_Adam.mq5 | 智能交易系统 | 一款采用 OpenCL 和 Adam 训练方法的分类神经网络 EA(输出层中有 3 个神经元) |
| 2 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 3 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
