在上一篇文章中,我试图提供一个关于主要机器学习模型创建步骤及其进一步实际应用的总体思路。在这一部分中,我想从简单的模型切换到具有统计意义的模型。由于创建一个基于机器学习的交易系统不是一个简单的任务,我们将从一些数据准备改进开始,这将有助于实现最佳结果。可以使用各种重采样技术来改进源数据的表示(训练示例)。本文将讨论其中一种技术。
上一篇文章中使用的标签的简单随机抽样有一些缺点:
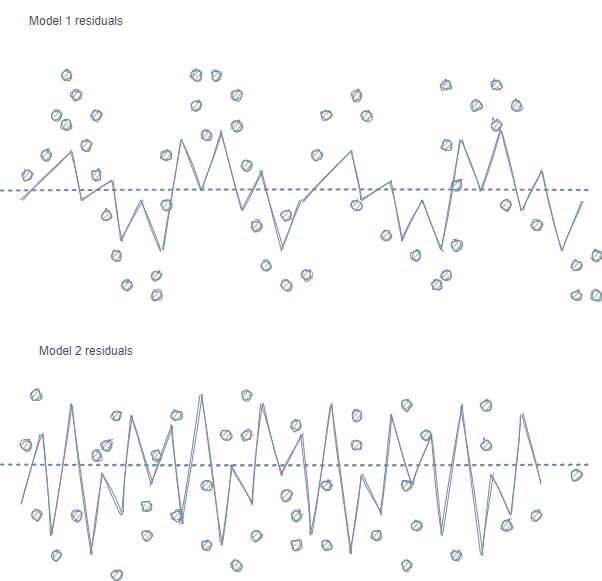
模型1具有残差的自相关,可以将其与某些市场属性的模型过度拟合(例如,与训练数据的波动性相关)进行比较,而其他模式则不考虑在内。模型2具有具有相同方差的残差(平均值),这表明模型覆盖了更多信息或发现了其他依赖性(除了相邻样本的相关性)。
对于分类也观察到了同样的效果,尽管它不那么直观,因为它只有几个类,与回归模型中使用的连续变量形成对比。然而,这种影响仍然可以通过皮尔逊残差和类似的度量来衡量。应该消除这些依赖关系(如模型1中的依赖关系)。

当使用随机抽样时,样本集可能有交叉,这可能导致不同类别的点之间的距离(例如,欧几里德距离)减小,并且导致同一类别的点之间的距离增大,这导致在训练阶段创建一个过于复杂的模型,具有许多分隔类别的边界。特征的微小偏差会导致模型预测从一个类跳到另一个类。这种影响破坏了模型在新数据上的稳定性,必须加以消除。
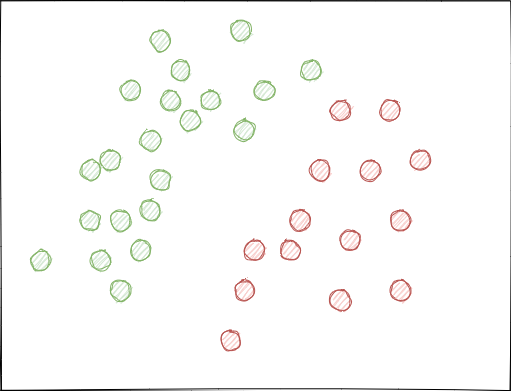
理想情况下,类标签不应在要素空间中相交,并且应线性(如下所示)或通过任何其他简单方法分开。此解决方案将为新数据提供更大的模型稳定性。
本文使用了前一部分中修改和改进的函数。载入数据:
LOOK_BACK = 5 MA_PERIODS = [15, 55, 150, 250] SYMBOL = 'EURUSD' MARKUP = 0.00010 TIMEFRAME = mt5.TIMEFRAME_H1 START_DATE = datetime(2020, 1, 1) TSTART_DATE = datetime(2015, 1, 1) STOP_DATE = datetime(2021, 1, 1) # make dataset pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=10, max=25, add_noize=0) res = tester(pr, plot=True) pca_plot(pr)
由于原始数据集的维数是20个特征(look_back*len(ma_periods))或任何其他大的特征,所以在平面上显示它不是很方便。让我们使用PCA方法,只显示5个主要组件,这将允许以最少的信息损失压缩特征空间:
如果您不熟悉PCA(主成分分析),请在谷歌中搜索。
def pca_plot(data): from sklearn.decomposition import PCA pca = PCA(n_components = 5) components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]])) components['labels'] = data['labels'].reset_index(drop = True) import seaborn as sns g = sns.PairGrid(components, hue="labels", height=1.2) g.map_diag(sns.histplot) g.map_offdiag(sns.scatterplot) g.add_legend() plt.show()
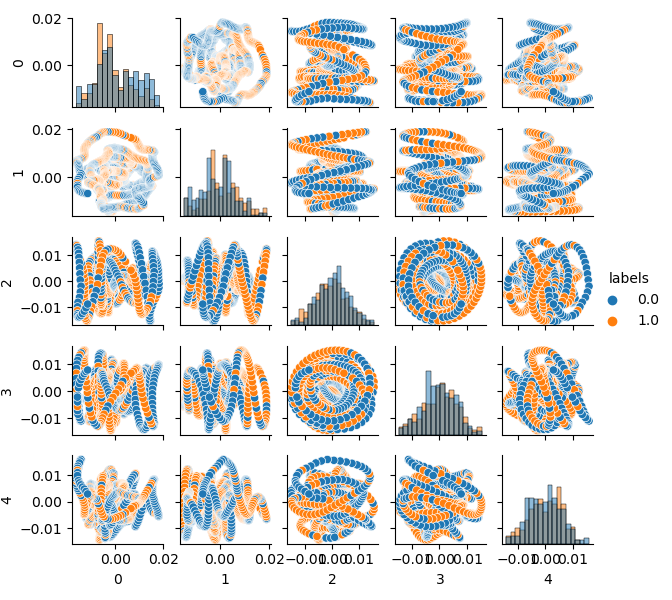
现在您可以看到每个组件对另一个组件的依赖性:这是二维特征空间,标记为类0和类1。组件对形成循环,这与通常的点云不同。这是由点的自相关引起的。如果你使这一行变细,环形就会消失。另一个事实是,这些类有很强的重叠。为了以最小的错误对标签进行分类,分类器必须创建一个非常复杂的模型,具有许多分割边界。我们可以说,原始数据集只是垃圾,而规则已经声明垃圾输入-垃圾输出(Garbage in — Garbage out,GIGO)。为了避免GIGO哲学,使研究更有意义,我建议改进机器学习模型(例如CatBoost)中原始数据的表示。
为了有效地将特征空间划分为两类,我们可以使用 K-means 方法实现聚类。这将给出如何理想分割特征空间的想法。
源数据集分为两个簇;显示五个主要组件:
# perform K-means clustering over dataset from sklearn.cluster import KMeans pr = get_prices(look_back=LOOK_BACK) X = pr[pr.columns[1:]] kmeans = KMeans(n_clusters=2).fit(X) y_kmeans = kmeans.predict(X) pr['labels'] = y_kmeans pca_plot(pr)
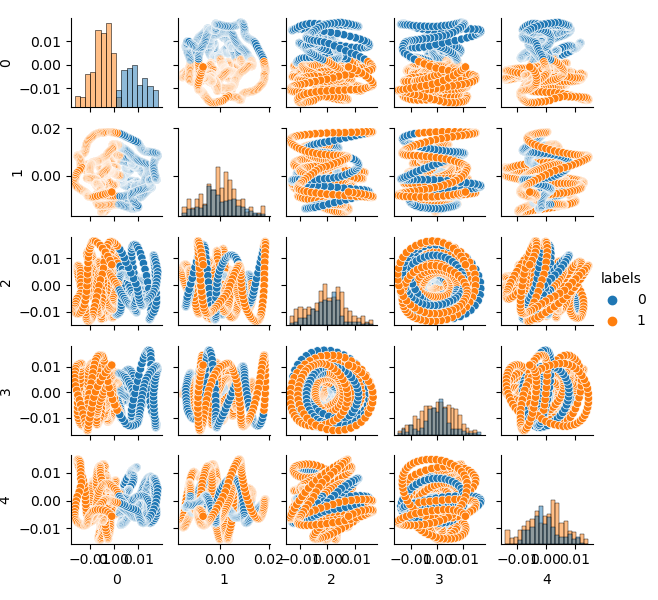
特征空间看起来很理想,但是类标签(0,1)显然不符合可以获利的交易。此示例仅说明了比GIGO数据集更合适的特征空间。这就是为什么我们需要在理想数据和垃圾数据之间进行折衷。这就是我们下一步要做的。
“我不能创造的,我就无法理解。”
—Richard Feynman
在本节中,我们将考虑学习“理解”数据并重新创建新数据的模型。
k-means 聚类方法相对简单,易于理解。但是,它有许多缺点,不适合我们的情况。特别是,由于它不是概率的,所以在许多实际情况下它的性能较差。假设这种方法将圆(或超球体)放置在给定数量的质心周围,其半径由簇的最外点确定。此半径严格限制每个簇的点集。因此,所有的簇只能用圆和超球体来描述,而真正的簇并不总是满足这个标准(因为它们可以是椭圆形或椭圆的形式)。这将导致不同簇值的重叠。
更先进的算法是高斯混合模型,该模型搜索多元高斯概率分布的混合,从而对数据集进行最佳建模。因为模型是概率的,所以这会输出一个实例被分类为特定集群的概率。另外,每个簇不是与一个严格定义的球体相关联,而是与一个光滑的高斯模型相关联,该模型不仅可以表示为圆,还可以表示为在空间中任意定向的椭圆。
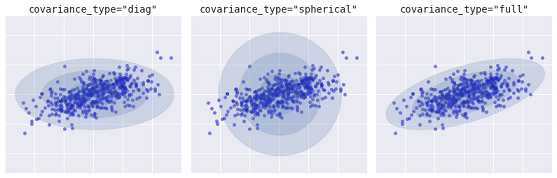
不同类型的概率模型,取决于 covariance_type (协变量类型)
下面是通过k-means和GMM获得的聚类的比较(来源):
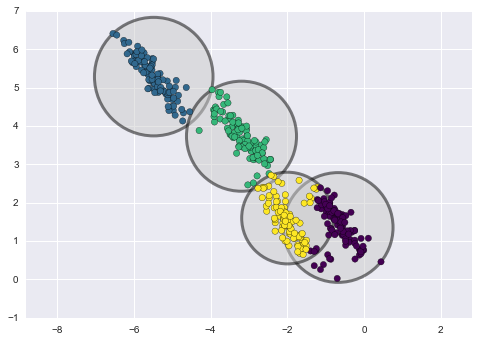
K-means 聚类
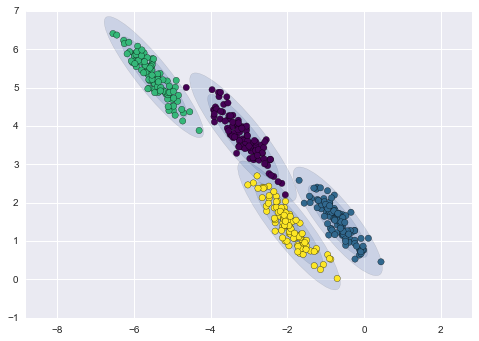
GMM 聚类
事实上,高斯混合模型(GMM)算法并不是真正的聚类算法,因为它的主要任务是估计概率密度。该模型中的聚类表示为从描述该数据的概率分布生成的数据。因此,在估计每个聚类的概率密度之后,可以从这些分布生成新的数据集。这些数据集将与原始数据相似,但它们具有或多或少的可变性,并且具有较少的异常值。此外,在许多情况下,数据集的相关性会降低。我们可以获得随机样本,然后利用这些样本训练 CatBoost 分类器。
首先,需要对源数据进行聚类,包括类标签:
# perform GMM clustering over dataset from sklearn import mixture pr_c = pr.copy() X = pr_c[pr_c.columns[1:]] gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)
可以选择的主要参数是n_components。根据经验,它被设置为75(簇)。其他参数不太重要,这里不考虑。模型训练后,我们可以从GMM模型的多元分布中生成一些人工样本,并可视化几个主要组成部分:
# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)
请注意,标签也已被聚集,因此它们不再表示二进制序列。标签再次转换为上述代码中的值(0;1)。现在,可以使用 pca_plot() 函数显示生成的特征空间:
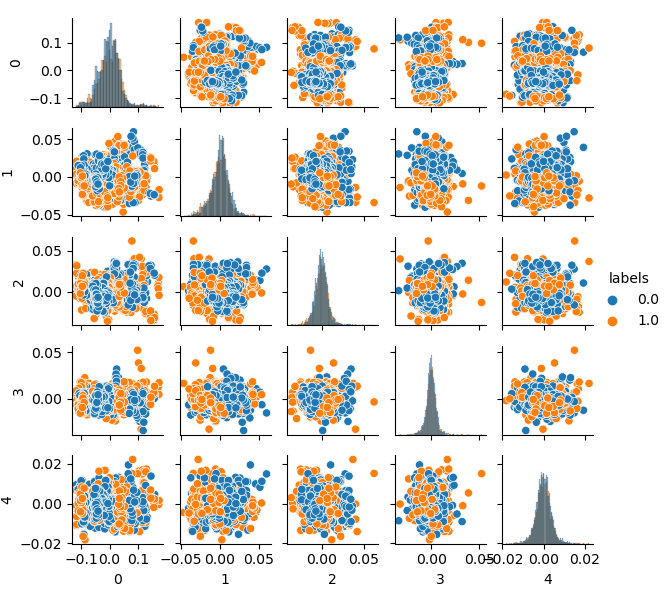
如果您将此图与前面介绍的GIGO数据集图进行比较,您可以看到它没有数据循环。特征和标签之间的相关性降低了,这应该会对学习结果产生积极的影响。同时,标签有时倾向于形成更密集的簇,模型可能变得更简单,划分边界更少。我们在消除垃圾数据问题方面取得了部分预期效果。尽管如此,数据基本相同,我们只是对原始数据重新取样。
如果GMM随机生成样本,这将导致数据的多元化。可以使用暴力算法选择最佳的模型,为此编写了一个专门的暴力算法函数:
# brute force loop def brute_force(samples = 5000): # sample new dataset generated = gmm.sample(samples) # make labels gen = pd.DataFrame(generated[0]) gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True) gen.loc[gen['labels'] >= 0.5, 'labels'] = 1 gen.loc[gen['labels'] < 0.5, 'labels'] = 0 X = gen[gen.columns[:-1]] y = gen[gen.columns[-1]] # train\test split train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True) #learn with train and validation subsets model = CatBoostClassifier(iterations=500, depth=6, learning_rate=0.1, custom_loss=['Accuracy'], eval_metric='Accuracy', verbose=False, use_best_model=True, task_type='CPU') model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False) # test on new data pr_tst = get_prices(TSTART_DATE, START_DATE) X = pr_tst[pr_tst.columns[1:]] X.columns = [''] * len(X.columns) #test the learned model p = model.predict_proba(X) p2 = [x[0]<0.5 for x in p] pr2 = pr_tst.iloc[:len(p2)].copy() pr2['labels'] = p2 R2 = tester(pr2, MARKUP, plot=False) return [R2, samples, model]
我已经强调了代码中的要点。首先,从GMM分布生成n个随机样本。然后利用这些数据训练 CatBoost 模型。函数返回测试器中计算的R^2分数。请注意,模型不仅使用训练周期数据进行测试,而且还使用早期数据。例如,该模型从2020年初开始接受数据培训,并从2015年初开始使用数据进行测试。您可以随意更改日期范围。
让我们编写一个循环,多次调用指定的函数,并将每次传递的结果保存到一个列表中:
res = []
for i in range(50):
res.append(brute_force(10000))
print('Iteration: ', i, 'R^2: ', res[-1][0])
res.sort()
test_model(res[-1])
然后对列表进行排序,列表末尾的模型具有最佳的R^2分数。让我们展示最好的结果:
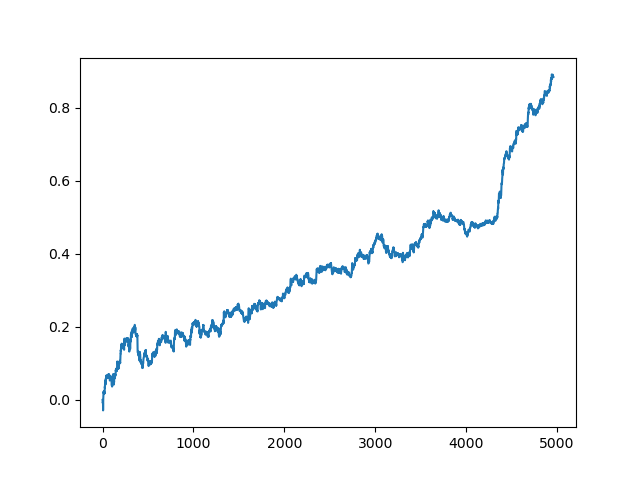
图表的最后(右)部分(约1000笔交易)是一个培训数据集,从2020年初开始,其余部分使用的是模型培训中未使用的新数据。由于模型按升序排序,根据R^2度量,我们可以用较低的分数测试以前的模型:
test_model(res[-2]) 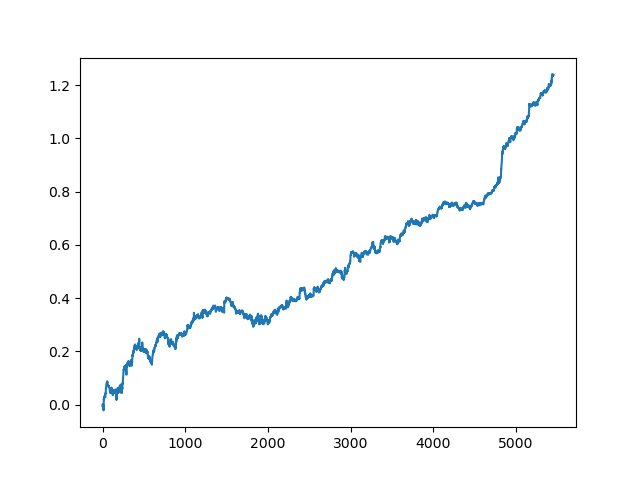
您还可以查看R^2分数本身:
>>> res[-2][0] 0.9576444017048906
正如你所看到的,现在这个模型是在一个很长的五年时间里测试的,尽管它是在一年的时间里训练的。然后,可以将模型导出为MQH格式。CatBoost模型对象位于嵌套列表中,索引为2—第一个维度包含模型编号。这里我们导出索引为[-2]的模型(排序列表末尾的第二个):
# export best model to mql export_model_to_MQL_code(res[-2][2])
导出后,可以在标准 MetaTrader 5 策略测试器中测试模型。由于自定义测试仪中的点差小于实际数据,因此曲线略有不同。不过,它们的大体形状是一样的。
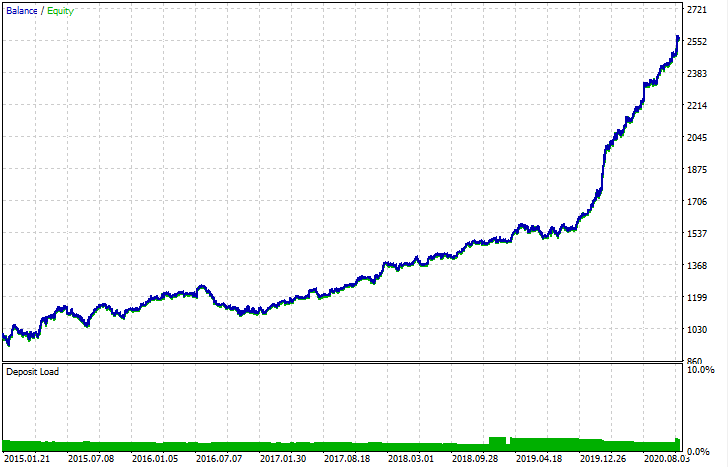
模型训练包含许多随机成分,这些成分每次都是不同的。例如,交易的随机抽样、GMM训练(也有随机性因素)、后验GMM分布的随机抽样和 CatBoost 训练(也有随机性因素)。因此,整个程序可以重新启动几次以获得最佳结果。如果无法获得稳定的模型,则应调整 LOOK_BACK 参数和移动平均数及其周期数。您还可以更改从GMM接收的样本数,以及训练和测试间隔。
对程序的 Python 代码进行了一些更改,它们需要一些澄清。
现在,可以设置具有不同平均周期的移动平均线列表。多个 MA 的组合通常对训练结果有积极的影响。
MA_PERIODS = [15, 55, 150, 250]
增加了测试过程、模型评估和选择的可配置开始日期。
TSTART_DATE = datetime(2015, 1, 1)
随机抽样函数经历了许多变化,添加了 add_noize 参数,允许您向原始数据集添加噪波。这将通过增加回撤和混合交易使交易变得不太理想。有时,通过引入0.1-02级的误差,可以在新数据上改进模型。
现在考虑到了点差,未涵盖点差的交易将标记为2.0的标签,然后由于不具信息性而从数据集中删除。
def add_labels(dataset, min, max, add_noize = 0.1): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True) if add_noize==0: return dataset # add noize to samples noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize) noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize) noize_b = noize_b+1 noize_s = noize_s-1 dataset.update(noize_b) dataset.update(noize_s) return dataset
tester 函数现在返回R^2分数:
def tester(dataset, markup = 0.0, plot = False): last_deal = int(2) last_price = 0.0 report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] if last_deal == 2: last_price = dataset['close'][i] last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 1 report.append(report[-1] - markup + (dataset['close'][i] - last_price)) last_price = dataset['close'][i] continue if last_deal == 1 and pred < 0.5: last_deal = 0 report.append(report[-1] - markup + (last_price - dataset['close'][i])) last_price = dataset['close'][i] y = np.array(report).reshape(-1,1) X = np.arange(len(report)).reshape(-1,1) lr = LinearRegression() lr.fit(X,y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.plot(report) plt.show() return lr.score(X,y) * l
通过主组件方法添加了数据可视化的辅助函数,这可能有助于更好地理解您的数据。
def pca_plot(data): from sklearn.decomposition import PCA pca = PCA(n_components = 5) components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]])) components['labels'] = data['labels'].reset_index(drop = True) import seaborn as sns g = sns.PairGrid(components, hue="labels", height=1.2) g.map_diag(sns.histplot) g.map_offdiag(sns.scatterplot) g.add_legend() plt.show()
代码分析器已经扩展,现在它考虑了移动平均值的所有周期,这些周期被添加到MQL程序中,之后 fill_arrays 函数形成一个特征向量。
def export_model_to_MQL_code(model):
model.save_model('catmodel.h',
format="cpp",
export_parameters=None,
pool=None)
# add variables
code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
code += 'int hnd[];\n'
code += 'int OnInit() {\n'
code += 'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'
count = len(MA_PERIODS) - 1
for i in MA_PERIODS:
code += 'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
count -= 1
code += 'return(INIT_SUCCEEDED);\n'
code += '}\n\n'
# get features
code += 'void fill_arays(int look_back, double &features[]) {\n'
code += ' double ma[], pr[], ret[];\n'
code += ' ArrayResize(ret,' + str(LOOK_BACK) +');\n'
code += ' CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
code += ' for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
code += ' CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
code += ' for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
code += ' ret[f] = pr[f] - ma[f];\n'
code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
code += ' ArraySetAsSeries(features, true);\n'
code += '}\n\n'
本文以一个简单的生成模型GMM(Gaussian Mixture Model,混合高斯模型)为例说明了如何对原始数据集进行重采样。该模型通过改进特征空间的特征,提高了CatBoost分类器在新数据上的性能。为了选择最佳的模型,我们已经实现了一个迭代数据重采样,有可能选择期望的结果。
这是一种从初级模型到有意义模型的突破。通过花费最少的精力开发一个交易策略的逻辑组件,你可以得到有趣的基于机器学习的交易机器人。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...