我是一个拥有超过5年经验的自动策略和软件开发人员。在这篇文章中,我将为那些刚刚开始外汇交易或任何其他交易的人揭开神秘的面纱。此外,我会尽量回答最流行的交易问题。
我希望这篇文章对初学者和有经验的交易者都有用。另外,请注意,这纯粹是我基于实际经验和研究的设想。
在我的产品中可以找到一些提到的机器人和指标。但这只是一小部分。我开发了各种各样的机器人,它们应用了大量的策略。我将试图展示所描述的方法如何让人们洞悉市场的真实本质,以及哪些策略值得关注。
如果你知道在哪里进入和退出市场,你可能不需要知道其他任何事情。不幸的是,出入场点问题是一个难以捉摸的问题。乍一看,您总是可以确定一个模式并遵循它一段时间。但是,如果没有先进的工具和指标,如何检测它呢?最简单且总是重复出现的模式是趋势和横盘。趋势是一个方向的长期运动,而横盘意味着更频繁的反转。
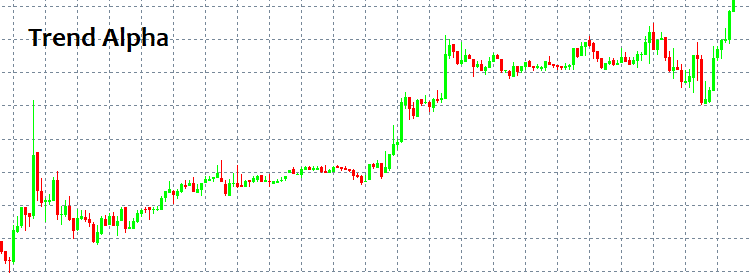
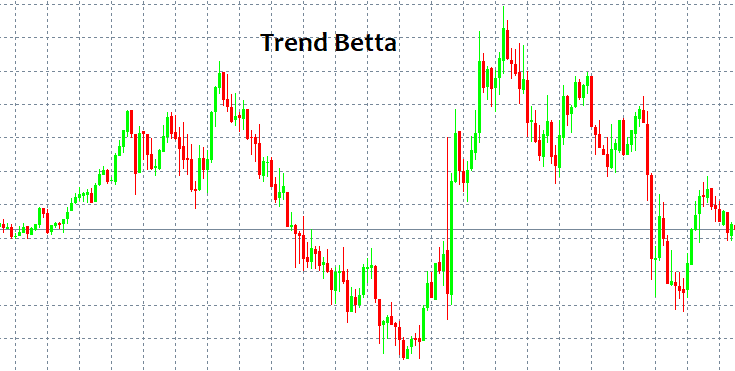

这些模式很容易被发现,因为人眼可以在没有任何指标的情况下找到它们。这里的主要问题是,我们只能在模式被触发之后才能看到它。此外,没有人能保证有任何模式。没有任何模式可以保住您的存款不被摧毁,无论使用什么样的策略。我将尝试用数学语言来提供可能的原因。
让我告诉你一些有关价格和使市场价格变化的动力的事情。市场上有两种力量——市场和限价。类似地,有两种订单——市价单和限价单。限价买家和卖家填充了市场深度,而市价买卖参与其中。市场深度基本上是一个垂直的价格尺度,表明那些愿意购买或出售的东西。在限价卖家和买家之间,永远有一个间隙,这个间隙叫做点差。点差是最佳买入和卖出价格之间的距离,以最小价格移动单位来衡量。买家想以最便宜的价格购买,而卖家想以最高价出售。因此,买方的限价单总是位于底部,而卖方的限价单总是位于顶部。标记买家和卖家进入市场深度,两个订单(限额和市场订单)相连。当限价订单被触发时,市场就会发生变化。
当一个活跃的市价订单出现时,它通常含有止损和获利。与限价订单类似,这些止损水平分散在市场四周,形成价格加速或反转水平。一切都取决于止损水平的数量和类型,以及交易量。知道了这些水平,我们就可以说价格可能加速或逆转。
限价订单也会形成难以通过的波动和集群。它们通常出现在重要的价格点,比如一天或一周的开盘。在讨论基于水平的交易时,交易员通常是指限价订单的水平。所有这些可以简单地显示如下。
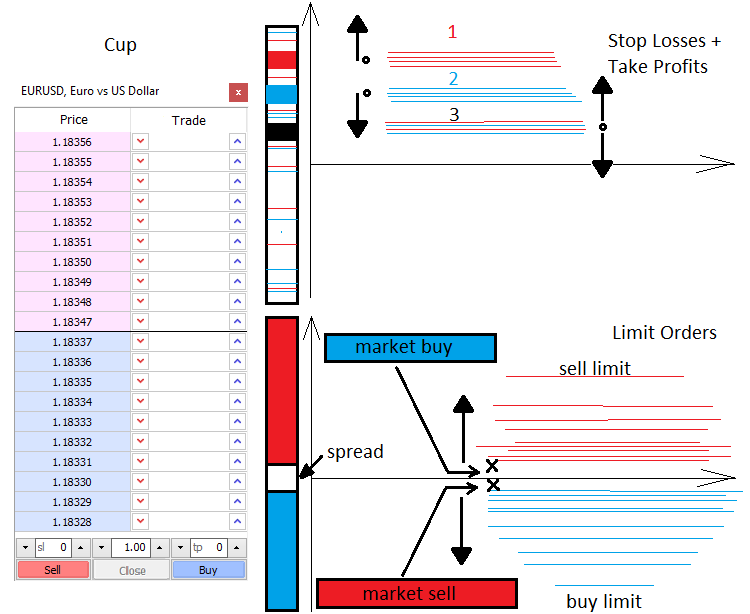
我们在 MetaTrader 窗口中看到的是t参数的离散函数,其中t是时间。函数是离散的,因为报价点(tick)的数目是有限的。在当前情况下,报价点是中间不包含任何内容的点。报价点是可能的价格离散化的最小元素,较大的元素是柱、M1、M5、M15烛形等。市场既有随机因素,又有模式因素。这些模式可以有不同的规模和持续时间。然而,市场在很大程度上是一个概率性的、混乱的、几乎不可预测的环境。要理解市场,就要用概率论的概念来看待市场。引入概率和概率密度的概念需要离散化。
为了介绍预期收益的概念,我们首先需要考虑术语“事件”和“穷尽事件”:
С1和С2事件形成一组完全相反的事件(即,在任何情况下都会发生其中一个事件)。因此,这些概率之和等于1 P2(tp,sl) + P2(tp,sl) = 1. 这个方程式以后可能会很有用。
在测试 EA 交易或者人工策略时,如果使用随机开启仓位,以及随机止损和获利,我们将会得到随机的结果,而预期收益会等于“-(点差)”,如果我们可以把点差设为0,结果就是0。这表明无论止损水平如何,在随机市场上我们总是得到零预期收益。在非随机市场上,只要市场具有相关的模式,我们总是得到一个损益。我们可以通过假设预期收益(Tick[0].Bid-Tick[1].Bid)也等于零得出相同的结论。这些结论非常简单,可以通过多种方式得出。
这是主要的无序市场方程描述了混乱使用限价水平打开和关闭订单的预期收益。在解完最后一个方程后,我们得到了所有我们感兴趣的概率,包括完全随机性和相反的情况,只要我们知道限价数值。
这里提供的方程只适用于最简单的情况,可以推广到任何策略。这正是我现在要做的,以达到一个完整的理解,什么构成了最终的预期回报,我们需要使它不为零。另外,让我们引入利润因子的概念,并写出相应的方程式。
假设我们的策略包括通过止损水平和一些其他信号来关闭仓位。为此,我将引入С3、С4事件空间,其中第一个事件通过止损水平关闭仓位,而第二个事件通过信号关闭仓位。它们也构成了一组完整的对立事件,所以我们可以用类比来写:
M=P3*M3+P4*M4=P3*M3+(1-P3)*M4, 其中 M3=P1*tp-(1- P1)*sl, 而 M4=Sum(P0[i]*pr[i]) - Sum(P01[j]*ls[j]); Sum( P0[i] )+ Sum( P01[j] ) =1
换句话说,我们有两个相反的事件。它们的结果形成了另外两个独立的事件空间,在这里我们也定义了完整的组。然而,P1、P2、P0[i] 和 P01[j] 概率现在是有条件的,而P3和P4是假设的概率。条件概率是假设发生时事件发生的概率。一切都严格按照总概率公式(贝叶斯公式)进行。我强烈建议你仔细研究一下,以掌握这件事。对于完全无序的交易, M=0.
现在这个等式变得更加清晰和宽泛,因为它考虑了通过止损水平和信号来关闭。我们可以更进一步地遵循这个类比,写出任何策略的一般方程式,甚至考虑到动态止损水平。这就是我要做的。让我们来介绍N个新的事件,形成一个完整的组,这意味着以类似的止损和获利来开始交易。CS[1] .. CS[2] .. CS[3] ....... CS[N] . 类似地, PS[1] + PS[2] + PS[3] + ....... +PS[N] = 1.
M = PS[1]*MS[1]+PS[2]*MS[2]+ ... + PS[k]*MS[k] ... +PS[N]*MS[N] , MS[k] = P3[k]*M3[k]+(1- P3[k])*M4[k], M3[k] = P1[k] *tp[k] -(1- P1[k] )*sl[k], M4[k] = Sum(i)(P0[i][k]*pr[i][k]) - Sum(j)(P01[j][k] *ls[j][k] ); Sum(i)( P0[i][k] )+ Sum(j)( P01[j][k] ) =1.
和之前 (更加简单) 的方程类似, 如果是无序交易并且没有点差,那么 M=0。你能做的最多的就是改变策略,但是如果它没有合理的基础,你只需要改变这些变量的平衡,仍然得到0。为了打破这种不必要的均衡,我们需要知道市场在任何一个固定的运动区间内向任何方向运动的概率,或者在一段时间内预期的价格运动收益。入场/出场点的选择取决于此。如果你设法找到他们,那么你将有一个有利可图的战略。
现在让我们来建立利润因子方程。PF = Profit/Loss. 利润因子是利润与亏损的比率。如果该数字超过1,则该策略是有利可图的,否则就不是。这可以使用预期收益重新定义。PrF=Mp/Ml. 这意味着预期净利润回报与预期净亏损的比率。让我们写下他们的方程式。
Sum(i)( P0[i][k] ) + Sum(j)( P01[j][k] ) =1.
为了更深入地理解,我将描述所有嵌套事件:
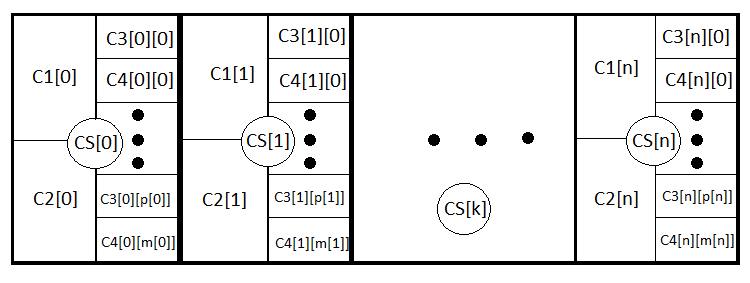
事实上,这两个等式是相同的,尽管第一个等式缺少与损失相关的部分,而第二个等式缺少与利润相关的部分。在无序交易的情况下,PrF=1,前提是价差再次等于零。M 和 PrF 是两个足以从各个方面评估策略的值。
特别是,有能力评估趋势或横盘性质的某一工具使用相同的概率理论和组合数学。此外,利用概率分布密度也可以从随机性中找出一些差异。
我将建立一个随机值分布概率密度图,其离散价格间隔固定的H步。让我们假设,如果价格向任何方向移动了H个点,那么就已经进行了一步。X轴是以垂直价格图的形式显示一个随机值,以步数计量。在这种情况下,需要n个步骤,因为这是评估整体价格变动的唯一方法。
在定义了这些数值之后,计算u和d:
要提供总的“s”向上移动步数(该值可以是负的,表示向下移动步数),应提供一定数量的向上和向下移动步数:“u”、“d”。最终的“s”向上或向下移动取决于总的所有步数:
n=u+d;
s=u-d;
这是一个由两个方程组成的系统。求解它得到u和d:
u=(s+n)/2, d=n-u.
但是,并非所有的“s”值都适合某个“n”值。可能的s值之间的步长始终等于2。这样做是为了给“u”和“d”提供自然数的值,因为它们将用于组合数学,或者更确切地说,用于计算组合。如果这些数字是分数,那么我们就不能计算阶乘,阶乘是所有组合数学的基石。下面是18个步骤的所有可能场景,该图显示了事件选项的范围。
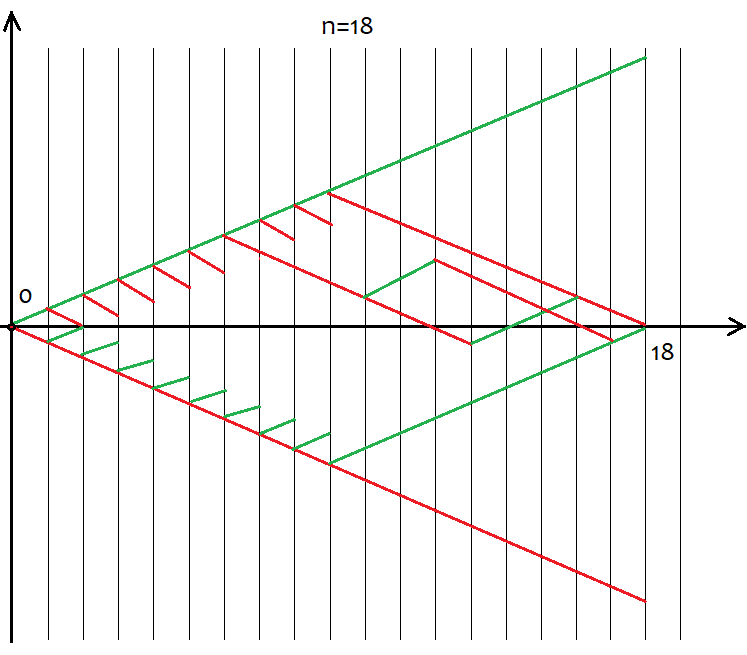
很容易定义期权的数量包括2^n,因为每个步骤后只有两个可能的移动方向-上升或下降。没有必要试图抓住每一个选项,因为这是不可能的。相反,我们只需要知道我们有n个独特的单元,其中u和d应该分别是向上和向下的。具有相同u和d的选项最终提供相同的s。为了计算提供相同“s”的选项总数,我们可以使用组合数学中的组合公式 С=n!/(u!*(n-u)!),以及等效方程С=n!/(d!*(n-d)!)。在u和d不同的情况下,我们得到了相同的C值。由于组合可以由上升段和下降段组成,这必然导致有重复。那么我们应该用什么片段来组成组合呢?答案是任意的,因为这些组合是等价的,尽管它们不同。我将在下面使用基于MathCad 15的应用程序来证明这一点。
现在我们已经确定了每个场景的组合数,我们可以确定特定组合(或事件,无论您喜欢什么)的概率。P = С/(2^n). 可以为所有“s”计算该值,并且这些概率之和始终等于1,因为这些选项中的一个无论如何都会发生。基于这个概率数组,我们可以在s步为2的情况下建立相对于s随机值的概率密度图。在这种情况下,可以简单地通过将概率除以s步长(即除以2)来获得特定步长处的密度。原因是我们无法为离散值建立连续函数。此密度保持与左右半步相关,即1。它帮助我们找到节点,并允许数值积分。对于负的“s”值,我将简单地镜像相对于概率密度轴的图形。对于偶数n值,节点编号从0开始,对于奇数n值,节点编号从1开始。在偶数n值的情况下,我们不能提供奇数s值,而在奇数n值的情况下,我们不能提供偶数s值。下面的计算应用程序屏幕截图阐明了这一点:
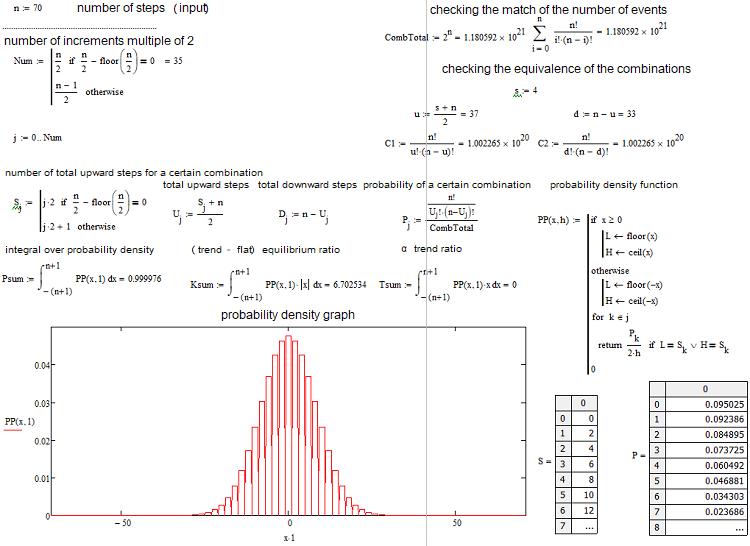
它列出了我们需要的一切。应用程序附在下面,这样您就可以尝试不同的参数。最热门的问题之一是如何界定当前的市场形势是趋势还是横盘。我已经提出了我自己的公式来量化一个工具的趋势或平坦性质。我把趋势分为阿尔法趋势和贝塔趋势。阿尔法意味着一种趋势,要么买要么卖,而贝塔只是一种趋势,继续运动,没有明确界定买或是卖。最后,横盘意味着回到初始价格的趋势。
不同交易者对趋势和横盘的定义差别很大。我试图给所有这些现象下一个更严格的定义,因为即使对这些问题及其量化方法有一个基本的理解,也允许应用许多以前被认为是死的或过于简单的策略。以下是主要方程式:
K=Integral(p*|x|)
或者
K=Summ(P[i]*|s[i]|)
第一个选项用于连续随机变量,而第二个选项用于离散随机变量。为了更清楚,我已经使离散值连续,因此使用了第一个方程。积分的跨度从负到正无穷大。这是均衡或趋势比率。在计算了一个随机值后,我们得到了一个平衡点,用来比较报价的真实分布和参考分布。如果 Кp > K, 市场可以被认为是趋势性的。富国 Кp < K, 市场就属于横盘。
我们可以计算出比率的最大值。它等于 KMax=1*Max(|x|) or KMax=1*Max(|s[i]|). 我们也可以计算出比率的最小值。它等于 KMin=1*Min(|x|) = 0 or KMin=1*Min(|s[i]|) = 0. KMid 是中点, 最小值和最大值是评估所分析区域的趋势或横盘性质所需的全部百分比。
if ( K >= KMid ) KTrendPercent=((K-KMid)/(KMax-KMid))*100 else KFletPercent=((KMid-K)/KMid)*100.
但这仍然不足以充分描述这种情况。还有需要解决的第二个比率 T=Integral(p*x), T=Summ(P[i]*s[i])。它基本上显示了上升步骤数量的预期收益,同时也是阿尔法趋势的一个指标。Tp > 0 表示买入趋势, 而 Tp < 0 表示卖出趋势, 也就是说 T=0 用于随机游走。
让我们找到这个比率的最大值和最小值: TMax=1*Max(x) 或者 TMax=1*Max(s[i]), 最小值的绝对值等于最大值, 只不过它是负的 TMin= - TMax. 如果我们测量从100到-100的α趋势百分比,我们可以编写与上一个类似的计算公式:
APercent=( T /TMax)*100.
如果百分比为正,则趋势为牛市,如果为负,则趋势为熊市。情况可能混合出现。可能存在α-横盘和α-趋势,但不同时存在α-横盘和α-趋势。下面是上述陈述的图解,以及为不同步数构造的密度图的示例。
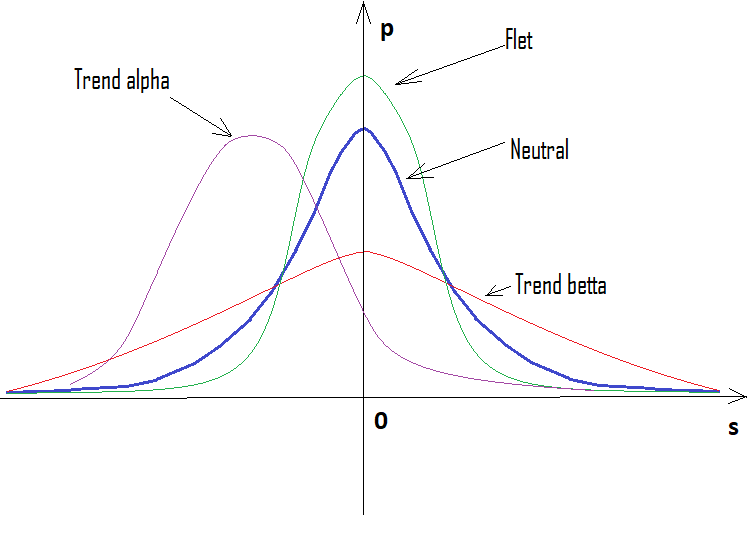
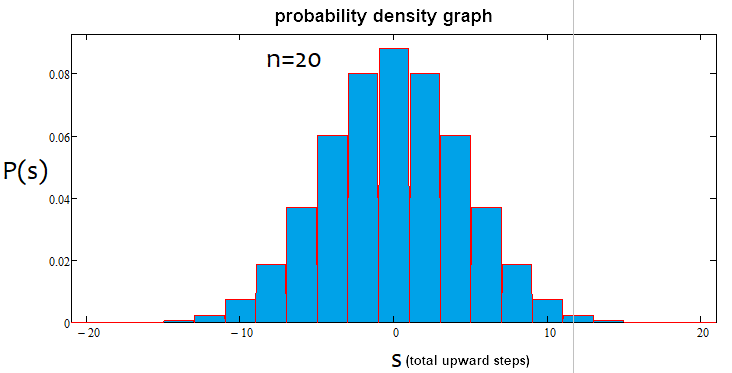
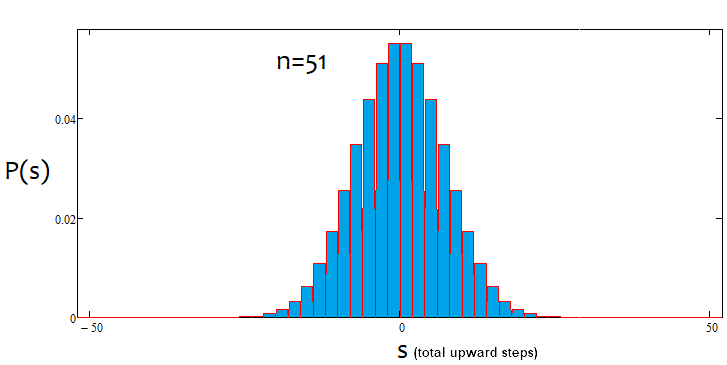
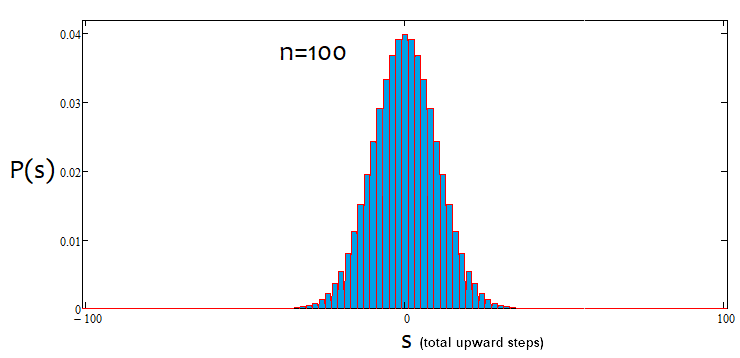
如我们所见,随着步数的增加,图形变得越来越窄,越来越高。对于每个步数,对应的alpha和betta值是不同的,就像分布本身一样。更改步数时,应重新计算参考分布。
所有这些方程都可以用来建立自动交易系统。这些算法也可以用来开发指标。一些交易者已经在EA中实现了这些功能。我确信一件事:应用这种分析比避免它要好。那些熟悉数学的人会马上想出一些新的方法来应用它,而那些不熟悉数学的人将不得不做出更多的努力。
在这里,我将把我简单的数学研究转化为一个指标,检测市场进入点,并作为开发EA交易的基础。我将使用 MQL5 开发指标。但是,代码要是可适应的,以便最大限度地移植到MQL4。一般来说,只有当代码变得不必要的麻烦和不可读时,我才尝试使用最简单的方法求助于OOP。然而,这在90%的情况下是可以避免的。不必要的彩色面板、按钮和图表上显示的大量数据只会妨碍视觉感知。相反,我总是尽量少用视觉工具。
让我们从指标的输入参数开始。
input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing ) input uint StepsMemoryI=2000;//Steps In Memory input uint StepsI=40;//Formula Steps input uint StepPoints=30;//Step Value input bool bDrawE=true;//Draw Steps
当指标加载时,我们能够以最后的烛形为基础,对一定数量的步数进行初始计算。我们还需要缓冲区来存储有关最后一步的数据。新数据将取代旧数据。它的大小是有限的。在图表上用同样的尺寸画步骤。我们应该指定步骤的数量,为其构建分布并计算必要的值。然后我们应该以点为单位告知系统步长,以及是否需要可视化步长。步骤要通过在图表上绘图来可视化。
我在一个单独的窗口中选择了指示器样式,显示中立分布和当前情况。有两条线,不过最好有第三条。不幸的是,指标功能并不意味着在一个单独的主窗口中绘图,所以我不得不求助于绘图。
我总是使用以下小方法来访问柱形图数据,就像在MQL4中一样:
//variable to be moved in MQL5 double Close[]; double Open[]; double High[]; double Low[]; long Volume[]; datetime Time[]; double Bid; double Ask; double Point=_Point; int Bars=1000; MqlTick TickAlphaPsi; void DimensionAllMQL5Values()//set the necessary array size { ArrayResize(Close,BarsI,0); ArrayResize(Open,BarsI,0); ArrayResize(Time,BarsI,0); ArrayResize(High,BarsI,0); ArrayResize(Low,BarsI,0); ArrayResize(Volume,BarsI,0); } void CalcAllMQL5Values()//recalculate all arrays { ArraySetAsSeries(Close,false); ArraySetAsSeries(Open,false); ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); ArraySetAsSeries(Volume,false); ArraySetAsSeries(Time,false); if( Bars >= int(BarsI) ) { CopyClose(_Symbol,_Period,0,BarsI,Close); CopyOpen(_Symbol,_Period,0,BarsI,Open); CopyHigh(_Symbol,_Period,0,BarsI,High); CopyLow(_Symbol,_Period,0,BarsI,Low); CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); CopyTime(_Symbol,_Period,0,BarsI,Time); } ArraySetAsSeries(Close,true); ArraySetAsSeries(Open,true); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); ArraySetAsSeries(Volume,true); ArraySetAsSeries(Time,true); SymbolInfoTick(Symbol(),TickAlphaPsi); Bid=TickAlphaPsi.bid; Ask=TickAlphaPsi.ask; } ////////////////////////////////////////////////////////////
现在,代码尽可能与MQL4兼容,我们能够快速轻松地将其转换为MQL4模拟。
为了描述这些步骤,我们首先需要描述节点。
struct Target//structure for storing node data { double Price0;//node price datetime Time0;//node price bool Direction;//direction of a step ending at the current node bool bActive;//whether the node is active }; double StartTick;//initial tick price Target Targets[];//destination point ticks (points located from the previous one by StepPoints)
此外,我们还需要一个点来计算下一步。节点存储有关自身和结束于其上的步骤的数据,以及指示节点是否处于活动状态的布尔组件。只有当节点数组的整个内存都被实节点填满时,才会计算实分布,因为它是按步骤计算的。没有步骤 - 就不计算。
此外,我们需要有能力在每个报价点(tick)更新步骤的状态,并在初始化指标时按柱形图进行近似计算。
bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node { if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and shift the array back { for(int i=ArraySize(Targets)-1;i>0;i--)//first move everything back { Targets[i]=Targets[i-1]; } //after that, generate a new node Targets[0].bActive=true; Targets[0].Time0=Time00; Targets[0].Price0=Price00; Targets[0].Direction= Price00 > StartTick ? true : false; //finally, redefine the initial tick to track the next node StartTick=Price00; return true; } else return false; } void StartCalculations()//approximate initial calculations (by bar closing prices) { for(int j=int(BarsI)-2;j>0;j--) { UpdatePoints(Close[j],Time[j]); } }
接下来,描述计算所有中性线参数所需的方法和变量。其纵坐标表示特定组合或结果的概率。我不喜欢称之为正态分布,因为正态分布是一个连续的量,而我建立了一个离散值的图。此外,正态分布是一个概率密度,而不是我们指标实例中的概率。建立概率图比建立密度图更方便。
int S[];//array of final upward steps int U[];//array of upward steps int D[];//array of downward steps double P[];//array of particular outcome probabilities double KBettaMid;//neutral Betta ratio value double KBettaMax;//maximum Betta ratio value //minimum Betta = 0, there is no point in setting it double KAlphaMax;//maximum Alpha ratio value double KAlphaMin;//minimum Alpha ratio value //average Alpha = 0, there is no point in setting it int CalcNumSteps(int Steps0)//calculate the number of steps { if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0); else return int((Steps0-1)/2.0); } void ReadyArrays(int Size0,int Steps0)//prepare the arrays { int Size=CalcNumSteps(Steps0); ArrayResize(S,Size); ArrayResize(U,Size); ArrayResize(D,Size); ArrayResize(P,Size); ArrayFill(S,0,ArraySize(S),0);//clear ArrayFill(U,0,ArraySize(U),0); ArrayFill(D,0,ArraySize(D),0); ArrayFill(P,0,ArraySize(P),0.0); } void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays { ReadyArrays(Size0,Steps0); double CT=CombTotal(Steps0);//number of combinations for(int i=0;i<ArraySize(S);i++) { S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ; U[i]=int((S[i]+Steps0)/2.0); D[i]=Steps0-U[i]; P[i]=C(Steps0,U[i])/CT; } } void CalculateBettaNeutral()//calculate all Alpha and Betta ratios { KBettaMid=0.0; if ( S[0]==0 ) { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=1;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } else { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } KBettaMax=S[ArraySize(S)-1]; KAlphaMax=S[ArraySize(S)-1]; KAlphaMin=-KAlphaMax; } double Factorial(int n)//factorial of n value { double Rez=1.0; for(int i=1;i<=n;i++) { Rez*=double(i); } return Rez; } double C(int n,int k)//combinations from n by k { return Factorial(n)/(Factorial(k)*Factorial(n-k)); } double CombTotal(int n)//number of combinations in total { return MathPow(2.0,n); }
所有这些函数都应该在正确的位置调用。这里的所有函数要么用于计算数组的值,要么实现一些辅助数学函数,前两个除外。它们在初始化期间与中性分布的计算一起被调用,并用于设置数组的大小。
接下来,以同样的方式创建用于计算实际分布及其主要参数的代码块。
double AlphaPercent;//alpha trend percentage double BettaPercent;//betta trend percentage int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option int Np[];//number of actual profitable outcomes of a specific case int Nm[];//number of actual losing outcomes of a specific case double Pp[];//probability of a specific profitable step double Pm[];//probability of a specific losing step int Sm[];//number of losing steps void ReadyMainArrays()//prepare the main arrays { if ( S[0]==0 ) { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)-1); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)-1); ArrayResize(Sm,ArraySize(S)-1); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i+1]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } else { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)); ArrayResize(Sm,ArraySize(S)); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } } void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps { ActionsTotal=(Size0-1)-(Steps0-1); } bool CalculateMainArrays(int Steps0)//count the main arrays { int U0;//upward steps int D0;//downward steps int S0;//total number of upward steps if ( Targets[ArraySize(Targets)-1].bActive ) { ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); for(int i=1;i<=ActionsTotal;i++) { U0=0; D0=0; S0=0; for(int j=0;j<Steps0;j++) { if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++; else D0++; } S0=U0-D0; for(int k=0;k<ArraySize(S);k++) { if ( S[k] == S0 ) { Np[k]++; break; } } for(int k=0;k<ArraySize(Sm);k++) { if ( Sm[k] == S0 ) { Nm[k]++; break; } } } for(int k=0;k<ArraySize(S);k++) { Pp[k]=Np[k]/double(ActionsTotal); } for(int k=0;k<ArraySize(Sm);k++) { Pm[k]=Nm[k]/double(ActionsTotal); } AlphaPercent=0.0; BettaPercent=0.0; for(int k=0;k<ArraySize(S);k++) { AlphaPercent+=S[k]*Pp[k]; BettaPercent+=MathAbs(S[k])*Pp[k]; } for(int k=0;k<ArraySize(Sm);k++) { AlphaPercent+=Sm[k]*Pm[k]; BettaPercent+=MathAbs(Sm[k])*Pm[k]; } AlphaPercent= (AlphaPercent/KAlphaMax)*100; BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100; Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen return true; } else return false; }
这里一切都很简单,但是有更多的数组,因为图形并不总是相对于垂直轴镜像。为了实现这一点,我们需要额外的数组和变量,但一般的逻辑很简单:计算特定案例结果的数量,然后除以所有结果的总数。这就是我们得到所有概率(纵坐标)和相应横坐标的方法。我不打算深入研究每个循环和变量。所有这些复杂性都需要避免将值移动到缓冲区的问题。这里的一切几乎都是一样的:定义数组的大小并对它们进行计数。接下来,计算alpha和betta趋势百分比,并将它们显示在屏幕的左上角。
它仍然是定义什么和在哪里调用。
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA); SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA); CleanAll(); DimensionAllMQL5Values(); CalcAllMQL5Values(); StartTick=Close[BarsI-1]; ArrayResize(Targets,StepsMemoryI);//maximum number of nodes CalculateAllArrays(StepsMemoryI,StepsI); CalculateBettaNeutral(); StartCalculations(); ReadyMainArrays(); CalculateActionsTotal(StepsMemoryI,StepsI); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { CalcAllMQL5Values(); if ( UpdatePoints(Close[0],TimeCurrent()) ) { if ( CalculateMainArrays(StepsI) ) { if ( bDrawE ) RedrawAll(); } } int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1; for(int i=0;i<ArraySize(Sm);i++) { iterator++; NeutralBuffer[iterator]=P[ArraySize(S)-1-i]; CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i]; } for(int i=0;i<ArraySize(S);i++) { iterator++; NeutralBuffer[iterator]=P[i]; CurrentBuffer[iterator]=Pp[i]; } return(rates_total); }
这里使用 CurrentBuffer 和 NeutralBuffer 作为缓冲区。为了更清楚,我介绍了离市场最近的烛形上的显示。每个概率都在一个单独的柱上。这使我们摆脱了不必要的麻烦。只需放大和缩小图表即可查看所有内容。这里不显示CleanAll()和RedrawAll()函数。它们可以被注释掉,不需要渲染就可以正常工作。此外,我还没有把绘图块包含在这里,你可以在附件里找到。那里没有什么值得注意的。指标也附在下面,有两个版本 — 用于 MetaTrader 4 和 MetaTrader 5,
如下所示。
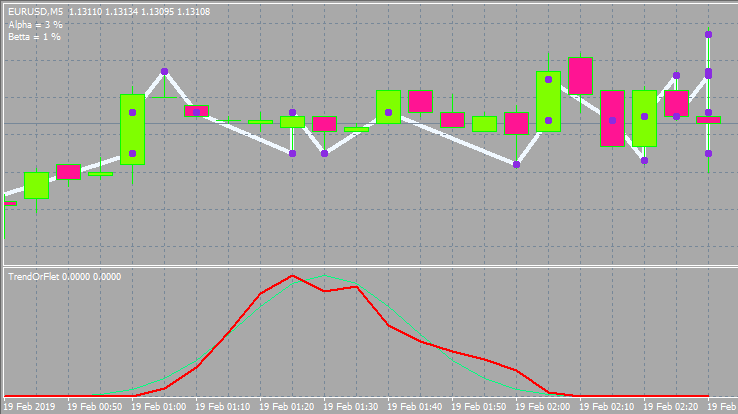
下面是带有其他输入和窗口样式的选项。
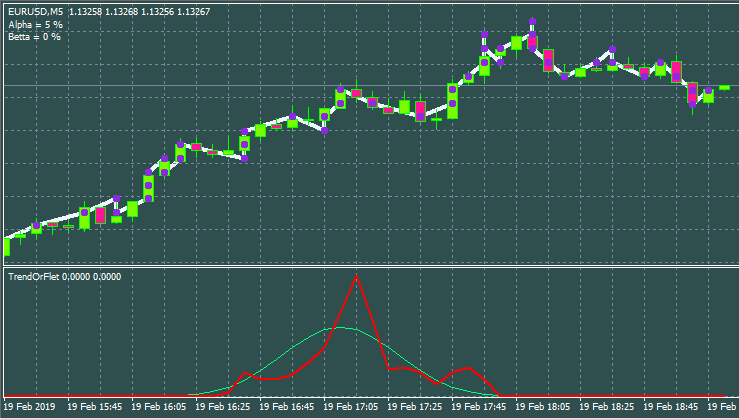
我已经看法并看过很多策略。以我微薄的经验,最值得注意的事情发生在使用网格或马丁格尔或两者兼而有之时。严格地说,马丁格尔和网格的期望收益都是0。不要被上升的图表所愚弄,因为总有一天你会损失惨重。市场上可以找到一些有效的网格 EA,它们工作得不错,甚至显示出 3 到 6 的利润银子,这是一个很高的数值。此外,它们在任何货币对上都保持稳定。但要想出一个能让你获胜的过滤器并不容易。上面描述的方法允许你把这些信号分类,网格需要一个趋势,而方向并不重要。
马丁格尔和网格是最简单而常见策略的例子,但是,不是每个人都能以正确的方法使用它们。自适应 EA 交易更加复杂一点,他们能够适应任何情况,无论是横盘,趋势或任何其他模式。它们通常涉及到从市场的某一部分寻找模式,并在短时间内进行交易,希望这种模式能保持一段时间。
另一组是由具有神秘、非传统算法的奇异系统组成的,它们试图利用市场的混乱性质获利。这种系统是基于纯粹的数学,能够在任何工具和时间段盈利。利润不大,但很稳定。我最近一直在处理这样的系统。这一组还包括基于暴力的机器人。暴力可以使用额外的软件来执行。在下一篇文章中,我将展示这样一个程序的我的版本。
基于神经网络和类似软件的机器人占据了顶部的环境。由于神经网络是人工智能的原型,这些机器人显示出非常不同的结果,具有最高的复杂度。如果一个神经网络经过适当的开发和训练,它能够显示出任何其他策略所无法比拟的最高效率。
至于套利,在我看来,它的可能性现在几乎等于零。我有类似的EA没有取得成效。
有人出于兴奋在市场上交易,有人寻找容易和快速的钱,而有人想通过方程和理论研究市场过程。此外,有些交易者没有其他选择,因为他们没有退路。我基本上属于后一类。以我所有的知识和经验,我目前没有一个盈利稳定的帐户。我有EA在测试中表现良好,但一切都不像看起来那么容易。
那些努力快速致富的人很可能会面临相反的结果。毕竟,市场不是为普通交易者创造的。它的目的正好相反。然而,如果你有足够的勇气大胆地进入这个话题,那么请确保你有足够的时间和耐心。结果不会很快。如果你没有编程技巧,那么你几乎没有机会。我见过很多伪交易者在完成20-30笔交易后吹嘘一些业绩。在我的例子中,在我开发了一个好的EA之后,它可能会工作一到两年,但是它不可避免地会失败……在很多情况下,它从一开始就不起作用。
当然,也有人工交易,但我认为它更类似于艺术。总之,在市场上赚钱是可能的,但你要花很多时间。我个人认为这不值得。从数学的角度来看,市场只是一条无聊的二维曲线。我当然不想一辈子都看烛形。
我相信圣杯是不可能的。我有相对简单的EA来证明这一点。不幸的是,他们的预期收益几乎无法弥补点差。我认为几乎每个开发者都有策略来证实这一点。市场上有很多机器人在各个方面都可以称为圣杯。但是用这样的系统赚钱是非常困难的,因为你需要为每一个pip而奋斗,同时还需要启用利差回报和合作计划。具有可观利润和低存款量的圣杯是罕见的。
如果你想自己开发一个圣杯,那么最好是看看神经网络。他们在利润方面有很大的潜力。当然,你可以尝试结合各种各样方法和暴力算法,我建议你马上深入研究神经网络。
奇怪的是,在我开发了大量的EA之后,关于圣杯是否存在以及在哪里寻找圣杯的问题的答案对我来说非常简单和明显。
所有交易者都想要三样东西:
第一点在这里是最重要的。如果你有一个有利可图的策略(不管它是手动的还是算法的),你总是想干预,这是不允许的。有利可图的交易比失败的交易少的情况下,会产生相当大的心理影响,破坏交易系统。最重要的是,当你处于亏损状态时,不要急于赢回你的损失。否则,你可能会发现自己损失更大。记住预期的回报。当前头寸的权益损失是多少并不重要。真正重要的是仓位总数和损益率。
下一个重要的事情是你在交易中的手数大小。如果你当前在盈利状态,确保逐渐减小手数。否则,就加大。但是,它只能增加到某个阈值,这是正向和反向的马丁格尔。如果你仔细想想,你可以开发自己的EA完全基于很多变化。这将不再是一个网格或马丁格尔,而是更复杂和更安全的东西。此外,这种EA可以在报价历史上的所有货币对上工作。这个原则即使在一个混乱的市场中也能起作用,无论你在哪里,如何进入,都无关紧要。如果使用得当,你将补偿所有的点差和佣金,如果使用得当,即使你在随机点和随机方向进入市场,你也将获得利润。
为了减少损失和增加利润,尽量在负半波买入,在正半波卖出。半路通常表示当前市场区域内的买方或卖方之前的活动,这反过来意味着其中一些已经是市场活动,而未平仓仓位迟早会平仓,将价格推向相反的方向。这就是为什么市场具有波动结构。我们到处都能看到这些波浪。购买之后是出售,反之亦然。用同样的标准平仓。
每个人的观点都是主观的。最后,一切都取决于你,不管怎样。尽管存在种种不利因素和浪费时间,但每个人都想创建自己的超级系统,收获自己决心的果实。否则,我完全看不到钻研外汇交易的意义。这项活动对包括我在内的许多交易者仍有吸引力。每个人都知道这种感觉叫什么,但听起来很幼稚。因此,我不会命名它,以免引战。)

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
