概述

在很久以前，金融市场形成初期，没有计算机，且在实际市场中进行实际商品交易时，将价格序列表示为时间间隔（或时间帧）的经典方法既已出现。 一天内的所有价格变化太多，很难加以存储。 甚至，它并没啥用，因为价格没有快速变化。 因此，显而易见的解决方案是按规则时间间隔记录价格值。 听起来合乎逻辑：“今天小麦的价格为 90 分，而昨天的价格为 80 分” 。一切都非常清晰：需求增长，价格上涨。 与今天的市场交易相比，成交并不多，这就是为什么价格重新定义很罕见的原因。

随着价格数据分析的出现和发展，它目标是更好地预测价格行为，并随着交易操作数量的增加，人们了解特定时间段最高价和最低价就变得很重要。 也就是说，昨天 80 分、今天 90 分的有关价格信息已不再足够。 人们想知道在指定时间段内，最高价和最低价触及何处。 那就是发明著名的烛条和柱线的时候。

随着交易操作数量的增加，价格序列的离散化变得越来越准确。 现在，我们已经用到分钟离散化，甚至有时更小的帧率，例如一秒和十秒。

价格序列按时间离散化的主要优点如下：

• 方便。 我们能确切地知道下一分钟将形成下一根柱线，并且我们将收到新的开盘价、收盘价、最高价和最低价。
• 资源效率。 如果不需要更高的精度，则烛条表示法在一个时间段内只能存储 4 位数字。 如果您打算存储出价、要价和最终价格的每次变化，那么一年的历史记录数量将非常庞大，高达数 GB。 如果您需要下载和存储 10-20 年的价格历史记录，且您关注的不只一个，而是 200-500 个品种，那么这将是一个真正麻烦。 甚或，需要庞大的计算机资源来处理 GB 字节的历史记录。 这就是为什么烛条分析和处理如今看起来更具吸引力的原因。
• 易于缩放和z直观分析。 当需要查看大图时，可以将离散化比例增加到数周甚至数月，并且在显示时可根据需要显示多个年份的数据。 如果需要更高的精度，则可以减小比例，甚至查看一分钟内正在发生的情况。 
• 时间线性。 在此演绎中，最方便的事情可能是每年间隔的历史记录在视觉上占用大约相同的屏幕空间。 在图表上查找前一年或前一小时既简单又直观。 直观上，时间的线性似乎是一个非常重要的参数，但有时候“正确”的决定是违反直觉的。
• 易于比较不同产品的价格。

信号离散化功能

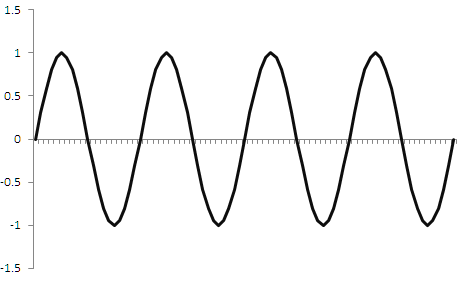
数据离散化不仅在交易中需要，而且在许多其他信号处理领域中也需要。 例如，在音乐中，原始的连续信号被数字化。 在进行编码时会利用时间离散。 按规则的时间间隔将信号幅度值写入存储器。 然后可以利用某些操作将该信号转换回连续信号。 连续信号离散化是一个经过充分研究的领域。 例如，遵循 Kotelnikov（Nyquist-Shannon 奈奎斯特）定理的规则指出：“如果离散频率是信号频率的 2 倍或更多，则可以完全恢复信号”。 因此，如果信号频率为 1 赫兹，则读取其幅度值时必须每秒至少 2 次（即频率为 2 赫兹）。 只有在这种情况下，才能在离散化后重获其原始形式。 图例 1 示意如果我们以 2 赫兹的采样率离散 1 赫兹的正弦波会发生什么。 信号显示为绿色，离散化的结果显示为红色。

图例 1.

离散化后，正弦波将被转换为三角波。 当然会有一些误差，但可用低通滤波器将该三角信号转换回正弦波。 这意味着我们可以恢复信号，并保留其思想，周期和幅度，尽管会有一些误差。 这样的失真在音乐中会被认为是至关重要的，但在交易当中则无关紧要。 但如果离散频率小于原始信号频率会如何？ 在下面的图例 2 中展示一个示例。

---->>

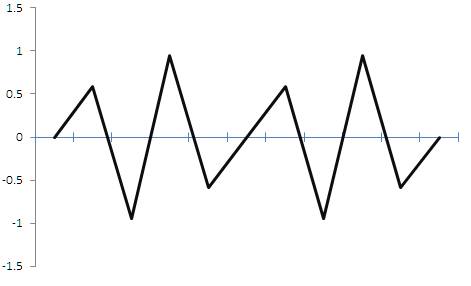
图例 2.

该示意图表明，如果离散频率小于信号频率两倍，则结果信号将大大失真，实际上我们收到的是一个与原始信号无关的随机信号。 当在交易里应用时，第一种情况将允许我们在发现高点时卖出，而在我们看到低点时买入。 还有，我们已知频率的情况。 错误的离散化之后，我们会丢失有关幅度和信号频率的信息。 由于选择了错误的离散频率，已知特征的确定周期性信号会变化为未知特征的随机非周期性信号。

从以上知识中得出两个合乎逻辑的问题：“在离散价格序列时，我们是否犯了错误？” 和 “价格序列是离散信号还是连续信号，其参数是什么？” 

答案并不简单，而是非常重要的。

价格序列是离散的还是连续的？

如果我们知晓市场价格形成机制，就可以回答这个问题。 我不会对其进行详述，因为在文章“ 以莫斯科交易所的衍生产品市场为例的交易定价原理”中已提供了详述。 一些参与者在市场深度里订单，而另一些参与者以所需价格买入所需额度。 这是价格图表形成时所发生的情况。 这些级别是离散的，即能够按一定的精度在 1、2、3 等价格下订单。 由于您可以购买1、2、3 个或更多单位，因此出价中设定的价格和由买方购买的数量也是离散的。 下面的图例 3 示意市场深度的示例； 您会看到价格和数量均为离散值。 

图例 3.

故此，我们可以得出结论，价格序列图表实际上是离散的。 在参与者买入离散性交易额度之后，价格沿着离散级别移动。 

价格的作用是什么

我们发现价格序列本身是离散的，但是价格变化是哪个参数的函数？

将音频信号离散化为规则间隔是可以接受的解决方案，因为音频信号是随时间变化的函数。 信号本身是取决于时间的幅度。 该信号属性是基本的。 这就是为什么于此没有问题的原因。

价格序列拥有不同的性质。 此处，幅度（价格）随时间变化，但时间不是价格变化的原因。 如果您试图找出价格变动的原因，那么问题就不那么简单了。 可以制定若干个假设：

1. 价格是交易的函数。 价格会随交易的执行而变化，因为交易操作会推动价格。 但是交易操作可能不会导致价格变化。 例如，有 10 支股票可用，价格为 1 美元。 参与者买入了 4 支股票，且剩余的 6 支股票价格相同。 因此，虽执行了交易操作，但价格没有改变。 但是，该操作把可提供此价格的交易量减低了，当下一位参与者买走了整个剩余交易量时，可能就会导致价格进一步变化。 价格仅在 1 美元的股票可供存量不足以满足需求，且可用额度被全部买走后才会发生变化。 在这种情况下，ASK（要价） 价格将升至 1.1 美元。 不过，其他参与者仍然能够以 1 美元的价格下订单，并将 ASK 价格回调。
2. 价格是市场上所有交易操作的函数。 价格不仅会当参与者在某个价位买断交易量的价格时发生变化，且在他们简单地取消订单，或将其移至其它价位时也会发生变化。 因此，随没有交易操作，但 BID（出价） 和 ASK（要价） 价格也会变动。
3. 价格是“收益”的函数。 价格可以变化，因为参与者为自己重新定义了资产价值。 重新定义资产价值可能有完全不同的原因。 无论任何情况下，资产价值的重新定义与参与者的利益密切相关。 从理论上讲，既定价格对包括买主和卖主在内的整体参与者来说都是最有利的（即便这种益处是负面的）。 最初创建市场是为了收益最大化，并判定买卖双方都可接受的最佳均衡价格。 该收益可能与某种资产无关。 例如，投资基金会需要紧急出售一种资产。 即使有亏损，他们也准备这样做，因为他们可以通过执行此操作获得其他好处，例如，他们可以购买其他资产，或向客户分红。 收益的性质可以不同。 在这种情况下，对于每位参与者，价格是针对收益每次重新定义的函数。
4. 价格是其自身的函数。 显然，每次价格变化都会导致市场参与者的收益发生变化。 收益能够在价格不变的情况下变化，但当价格变化时，参与者的收益也会改变。 这并非对价格变化的最准确描述，但它令我们能够大致逼近理想模型，并做出一些假设，这些假设对将来的结果不会产生重大影响。 基本交易价格变化。 即使我们选择了分红策略（忽略价格），支付分红最终也会导致价格变化。 在这种情况下，价格变化是将图表向左平移的信号。 仅当价格移动 1 个点时，才会记录价格变化。 可以使用任何步长，具体取决于偏好的尺度：每次向上或向下移动 n 个点时，都可以记录价格值。 

我认为第三种选项最有可能，说明价格是重定义收益的函数。 但是不可能为了离散序列而计算每名参与者的收益。 在前两种情况下，可以计算出交易所市场中的交易和非交易操作，但是也有困难。 例如，一种资产可以在两个或多个不同的交易所进行交易。 或是，如果存在资产的衍生产品，例如期货和期权，我们是否需要计算与资产间接相关的操作？ 这些问题需要单独进行大量的研究。 在任何情况下，这四种情况都是间接相关的。 第四个选项，在于价格是其自身的函数，能够进一步的研究，前提是我们假设这是一个粗糙的模型。

资产价格的变化率取决于交易数量。 交易操作越多，价格变化就越频繁，这就意味着其中存在直接的相关性。 相应地，如果市场上有很多参与者，他们会进行很多交易操作，从而会导致每名参与者的收益更频繁地重新定义。 从而，每名参与者会尝试更频繁地重新定义价格，从而导致更多的交易，故资产价格变化的频率将很高。

依时间间隔和随机分量进行价格序列离散化的特征

根据我们的粗略模型，价格是其自身的函数，并且仅当价格变化一定点数时才离散化价格。 即使这不是很正确，该假设也将令您对该主题有进一步的了解，且不会影响最终结果。 甚或，为了能盈利，我们需要知道价格已经改变。 另外，我们需要知道它是如何变化的，从而据此搜索形态。 

价格每浮动 1 个点数（此处一个点数是价格最小的可能变动）将等于一个步长。 我们看看时间序列离散后会发生什么。 显然，每单位时间内价格覆盖的点数取决于交易活动。 交易活动（执行的交易操作数）越高，价格最终将经历的步长越多。 交易活动与价格变化没有直接关系，但价格变化取决于交易活动：交易活动越高，价格变动就越多。 依赖性是间接的，但相关性为正。 假设一步长是 10 个点数。 在示例中将使用一小时的烛条。 下面的两个示意图展示的是以砖形表示的价格。 这些砖形类似于 Renko 柱线，但它们所依据的构造原理略有不同。 它们使用经典烛条的最高价和最低价，在砖块形成时间显示最高价和最低价。 像烛条一样，砖形拥有 4 个特征：开盘价、最高价、最低价和收盘价。 与烛条的区别在于，开盘价和收盘价之间的距离始终是固定的，并以点数为单位表示。 当价格垂直覆盖 N 个点数时，该砖形收盘。 例如，块形大小为 10 个点数。 一旦价格垂直移动 10 个点数后，该砖形收盘，一个新的砖形开始。

图例 4.

如果一个转形等于一个 N 点数的一个步长，那么我们来看看一小时烛条内部发生了什么。 图例 4 示意在形成一小时烛条期间发生的走势。 在上图中，价格在一小时内垂直覆盖了 10 块砖。 如果砖形大小为 10 个点数，则烛条大小为 100 个点数。 在整个烛条的形成时间里，总共有 25 块砖形成，这等于 25 个步长。 下图显示了另一个示例，其中在烛条形成期间，价格移动了 0 块砖，或 0 个点数。 在价格形成期间，价格总共移动了 40 块砖，或 40 个步长。 现在，我们来查看包含此类烛条的图表。 如图例 5 所示。 烛条每小时收盘一次，价格序列绝对不是时间的函数。 在简化情况下，它是交易操作的函数，交易操作与覆盖的点数成正相关。 由于我们将点数转换为砖形，因此砖块数量与交易数量呈正相关。 实际上，每个烛条（假设一小时）实际上具有随机数量的砖形，或每个步长 N 个点数。 进而，我们将了解为什么这很重要。 这是因为尽管市场上发生了一些交易，但烛条在一定时间后依然按时收盘。 时间是一个外部参数，与价格过程仅有一点的相关性。 换言之，价格变化不是因为经过了一个小时，而是由于其他一些原因，其中之一也可能是流逝的时间。

图例 5.

交易活动会随着时间的推移而发生显著变化。 此外，不同交易产品的交易活动是不同的。 此外，算法交易的发展导致每个时间单位内的操作数量和交易额的增加，这意味着在 2010 年和 2020 年之间进行直接烛条比较是不正确的，因为每根烛条包含的操作次数不同。

现在，我们进一步简化，然后随机漫游入场。 当然，市场不是随意漫游的，但这种方式，会更容易理解它。 稍后，我们将回到实际市场。

中心极限定理指出，足够大量的具有近似相同比例的弱相关随机变量的总和（没有一项对总和具有支配性或决定性的贡献）大致呈正态分布。 当应用于我们的情况时，我们可以从该定理得出结论，平均而言，我们的随机过程将覆盖 N 个步长的距离，该距离与步长的平方根大致成正比。 如果一块砖形是 1 个步长，那么对于 100 块砖形，平均价格将垂直覆盖 100^0.5 = 10 块砖形。 在个别情况下可能会有所不同，但平均而言，随机序列将遵循正态分布规则。 此随机序列的步长数量稍微依赖时间，因为步长数量是由价格活动生成的，而价格活动随时间的变化很大。

因此，随机价格系列的一小时烛条的大小，平均而言与 N^0.5 成比例，其中 N 是烛条台内部的步长数量。 这意味着一小时烛条的大小将服从正态分布律。 进而，考虑到烛条中可以存在随机的步长数量这一事实，我们可以得出结论，烛条尺寸也将服从正态分布定律。 即，烛条大小等于该烛条内步长数量的平方根。 我们来验证一下此声明。 为此目的，我将使用 50,000 根 1 分钟的 GBPUSD 烛条，持续时间为 2020.05.18 至 2020.07.03。

1. 我们发现一分钟烛条平均大小的模值 - 这将作为步长。 为此，从每下一根烛条的收盘价中减去每前一根烛条的收盘价，并取模值。 我得到了 1 分钟 GBPUSD 烛条的平均大小 = 0.000170
2. 现在，我们找到同一时期一小时烛条的平均大小（一小时烛条包含 60 根 1 分钟烛条）。 为此，从下一个小时烛条的收盘价中减去前一个小时烛条的收盘价，并取模值。 我得到了一小时 GBPUSD 烛条的平均大小 = 0.001117
3. 现在，如果我们假设价格序列是随机漫游的，那么我们现在来找出每小时覆盖的平均价格应该是多少。 要找到此数值，请将 1 分钟烛条的平均大小乘以步长数量的平方根，再乘以平均步长。 我们有 60 => 0.000170*(60^0.5) = 0.001315。 如果原始系列遵循正态分布定律，则一小时烛条的大小将趋于该平均大小值。
4. 我们比较实际烛条和随机漫游烛条的平均大小（实际 0.001117）≈（理论 0.001315）。 差值仅有 0.0002。 由此可得出结论，我们关于烛条尺寸服从正态分布定律的假设是正确的，并由真实品种的市场数据所证实。 0.0002 的差值不明显。

此外，使用获得的一小时烛条，我们实际上组合并分析了价格序列某些片段的序列，其幅度遵循正态分布定律。 自然，如果我们移到更高的时间帧，我们将得到全部相同的烛条，烛条的大小与步长数量的平方根成正比。 现在回到图例 2：如果一个序列被错误地离散，输出结果将是一个随机序列。 实际上，经由时间离散化，我们将价格序列转换为随机序列。 好吧，时间离散序列仍然可以具有形态，因为市场不是随机序列，它与时间具有间接依赖性，但是分析这样的序列和识别形态变得更加困难。 这是时间离散，导致价格序列中的所谓“噪声”和非平稳性 - 人们经常对此进行讨论，但没人解释过这些噪声的来源。 现在，噪声不仅当信号离散化时会出现，而且还包括一个随机分量，出现这种情况是由于价格序列的离散化参数不正确，因其本身就是离散的。

为了确保我们由一小时烛条获得的结果不是偶然巧合，我们针对日线烛条重复相同的过程。 每天有 24 小时。 由于货币对是全天交易的，因此我们假设日线烛条包含 1440 根 1 分钟烛条。 我们针对 H1 采用与 1 分钟数据相同的采样间隔。 这次，为方便起见，相关数据以表格形式表示。

如您所见，如果不是一个真正的行情，而是一个随机漫游，则日线烛条的实际平均大小与理论预测的大小不会有太大差异。 包含历史数据和计算结果的 Excel 文件如下。

为了计算较高时间帧烛条的平均大小，我们采用了 1 分钟时间帧数据。 但是，如果我们得到比即时报价数据更低的价格 - 将会产生不同的结果吗？ 我们要做的是：

1. 以相同时间段（从真实帐户）中获取 1 分钟烛条的即时报价数据，并计算一分钟烛条的平均即时报价次数 - 平均数字为每分钟 59.99 次即时报价。 
2. 加载即时报价数据，并找出平均即时报价大小，它等于 0.000014378。 
3. 计算 1 分钟烛条的理论大小为 (59.99^0.5)*0.00014378=0.000111363
4. 计算一小时烛条的理论大小为 ((59.99*60)^0.5)* 0.000014378= 0.00086

如您所见，M1 和 H1 烛条的平均尺寸与理论值相差无几，如果是随机漫游，价格序列将具有该理论值。 由此，我们可以得出结论，由于某种原因，价格序列的行为就像是随机漫游，这可能是由于时间间隔的不正确离散所致。

价格序列增量的分布密度

定量评估可以粗略估计价格系列烛条尺寸如何与随机漫游烛条尺寸相对应。 绘制价格序列增量分布密度更有趣，这将令我们能够直观地评估其与随机漫游增量分布密度的相似性或差异。

分析的重要部分是数据准备。 增量密度将依据价格在 60 分钟（1 小时）内（即 60 步）移动的点数进行计算。 此处，我们需要知道 1 分钟烛条的平均大小和步长数量（1 分钟烛条中 1 分钟烛条的数量）。 我们已经计算过 1 分钟烛条的平均大小 - 等于 0.000170。 1 分钟烛条中 1 分钟烛条的数量是 60。 这意味着价格每小时可以走 60 步，每步为 0.000170。 因此，极端情况是价格从起点连续上涨 60 个点数，或下跌 60 个点数。 因此，分布密度估计是在 -0.00017*60=-0.0102 和 0.00017*60=0.0102 之间的范围内。 换言之，我们知道如果价格仅上涨，且步长为 0.00017，那么它将在 60 步（在一小时内）达到最大值 0.0102。 此外，对于 60 步，价格只能采用离散级别 0、0.00034、0.00068、0.00102 ... 0.0102 和类似的负数值。 图例 6 示意价格为何会恰好位于这些级别。

图例 6.

如果某个离散函数从零点数开始，其步长等于 1，并执行 6 步，则它最终可以垂直移动 6、4、2 或 0 个段落，并且只能采用双倍步长的离散值。 我们的情况类似：如果 1 分钟烛条的平均大小为 0.00017，那么价格可以采用离散级别，其间隔等于烛条大小的两倍。 实际上，烛条可以具有不同的大小，不仅是 0.00017，这就是价格可以取中间值的原因。 因此，为了进行分析，我们将统计落入间隔内的，有两倍平均蜡烛大小的事件。 为了找到价格序列分布结果的差异，将其与随机漫游的分布进行比较。 随机漫游的特征是，每个下一步的方向变化概率为 50％，且没有记忆。 图例 7 以黑色示意价格序列的概率密度分布，以红色示意随机漫游的概率密度分布。

图例 7.

从图例 7 可以看出，价格序列概率分布密度几乎与随机漫游概率分布密度相匹配。 与随机漫游分布密度相比，价格序列概率分布密度拥有略高的峰值，略窄，且略微向右偏移。 这表明价格序列中每个下一步出现逆转的可能性略高于 50％，并且有小型的上升趋势，但这些差异并不大。 从这种偏差中获利似乎并不很困难，但我们将在下一篇文章中进行讨论。 在此，我们取理想的随机变量进行处理，该随机变量具有足够大的样本，将趋向基准。 使用表格绘制随机漫游的概率密度分布图，其中的一部分如图例 8 所示。

图例 8.

该概率密度分布图证实了我们早前的结论，即烛条尺寸（在这种情况下为 H1 烛条）趋向于价格序列随机漫游烛条。 它还可通过直观更准确地评估这一事实。

本文中提到的所有数据和计算都附带在下面的 xlsx 文件之中。

高低波动区

细心的交易者可能会注意到，行情上的烛条通常按“大”和“小”尺寸分组（波动率高和低的区域），这意味着图表不是随机漫游，而是有形态的。 如果时间离散引入了严重的失真，则不会观察到这种效果。 然而，可以通过以下事实来解释此事实：烛条大小取决于在此烛条内执行的交易操作的数量。 这该如何验证？ 您可以简单地查看带有即时报价交易量的图表 - “小烛条”时段伴随着较低的即时报价次数，而“大烛条”时段伴随着较高的即时报价次数。 如果我们假设一次即时报价就是一步，那么价格在“大烛条”期间会走更多的步数，但是烛条的大小仍然与步数的平方根乘以平均步长成正比（图例 9 中的示例） 。 即时报价的交易量则与交易活动直接相关：交易越活跃，单位时间内经历的交易次数就越多。 交易所市场提供了真实交易量的历史记录，您可以在其中看到即时报价交易量与真实交易量密切相关，这也表明交易量与交易活动强度之间的关系。

图例 9.

这也证明了时间离散化对最终的价格序列形式造成了严重的扭曲，从而令价格分析更加困难。 这种扭曲导致了另一类交易系统的出现，即所谓的“夜间剥头皮”。 我并不是说它们不能产生利润，但是在开发这样的系统时有必要考虑价格序列代表的这种特殊性，并进行额外的研究以便回答以下问题：“是否存在逆转的可能性？这些区域真的比趋势延续的可能性高吗？”，和 “这些区域的统计特征是否可以产生利润？”，因为此类系统均是基于这种形态的。 

替代价格序列离散化

上述分析的简单结论表明，即时报价数据更适合处理和分析，因为它们避免了价格序列中的离散化误差。 如果需要更大的尺度，我们将使用 10 或 100 个即时报价的砖形。 但问题在于，即时报价本身也是离散化的一种方法。 这种方法被广泛采用，但由于价格不是接收到的即时报价的函数，因此它仍然会在过程中引入失真。 价格至少是已执行交易的函数，而交易也许并不总会产生即时报价。 交易所的即时报价与真实交易有某种联系。 但是在外汇市场上，每家公司都可以提供任意数量的即时报价，并且很难辨识哪个是正确的。 因此，即使我们简单地假设价格是交易的函数，也很明显，即时报价会扭曲价格序列，并引入可能导致错误的随机分量。

相应的离散问题是数据分析的重要组成部分。 例如，图例 10 示意两个比特币兑美元价格的图表。 上面的图表是周线常规烛条图表，下面的图表以 N 个点数为砖形离散化。 它是相同的周期，相同的砖形数量/烛条数量，但离散方法不同。 您可以看到相同资产的图表不同。 自然而然的问题出现了：“这两种表述哪个是正确的？”

图例 10.

我得出的结论是，正确的显示应考虑到价格序列的离散性。 然而，由于离散性的性质仍然未知，因此运用这种离散化方法，其反映我和其他市场参与者所产生的盈亏将会“更准确”。 因此，最好根据构成我们收益的数据进行分析。 也就是说，我们不应该考虑价格的即时变化，而应该只考虑价格变化了多少。

时间离散化的另一种备案是固定幅度离散化，其中假定价格是其自身的函数。 这些是我们早前讨论的砖形。 价格垂直移动 N 个点数后，将 N 个点数的砖形收盘。 也许这不是最好的方法，但是我们对价格已覆盖了多少个点数感兴趣，因为这会影响我们产生的盈亏。 甚至，每个参与者的利益在价格垂直超过 N 个点数后就会发生变化。 这意味着价格是其自身函数的模型最接近真实交易。 图例 11 示意以固定大小的砖形离散的正弦曲线。 形状丢失了，但保留了主要特征，包括周期和幅度。

图例 11.

即使离散化参数设置不正确，仍将保留幅度和周期的数值。 图例 12 展示了一个示例，说明砖形尺寸太大时会发生什么。 砖形内的部分信息会丢失，因此准确性较差（数据压缩不可避免），但保留了有关幅度和周期的信息。 如果砖形尺寸大于价格序列幅度，则不会显示砖形。 因此，与图例 2 相对比，如果选择了错误的离散化参数，则原始确定性信号不会变成随机信号。

图例 12

这样可以消除时间离散价格序列时引入的随机分量，以及在源序列的参数函数未知的情况下。 此方法比时间离散化效果更好，并且可以方便地缩放图表，缩放比例可达精度最高的 1 个点数。

结束语

• 价格序列的性质是离散的，其源于定价结构。
• 市场价格不是时间的函数，而是与经济过程紧密相关的函数，目前不太可能将它们全部考虑在内。
• 将价格序列离散化为时间间隔会引入明显的随机分量； 这扭曲了价格图表的真实形状，给带有未知参数的复杂过程增加了噪音和不稳定。
  
• 在开发价格序列离散化方法时，必须要考虑价格是哪个参数的函数。
• 除其他原因外，由于不正确的离散化参数，导致价格序列不稳定。
• 可以分析时间离散的价格图表，从而找到形态，但有必要考虑上述方面，以便更好地理解所发现形态的特殊性质。
• 思路是开发其他价格序列离散化方法，这些方法在原始数据中引入的失真要小得多。 本文当中已介绍了一种这样的方法。
• 在开发交易算法和统计市场研究时，应考虑所用价格序列离散化的特殊特征。