在第一篇文章中,我们阐述了市场记忆的概念,该概念的确定可作为某种顺序的价格增量的长期依赖性。 我们还进一步研究了市场中存在的“季节性形态”的概念。 直至目前,这两个概念是分开存在的。 本文之目的是展示“市场记忆”的季节性,它通过在紧凑的时间段内任意顺序增量的最大相关性,以及在远期时间段内的最小相关性来表达。
我们提出以下设想:
价格增量的相关性取决于季节形态的存在,以及附近增量的集簇。
我们尝试以一种随性直观且略带数学风格的方式来确认或反驳它。
根据经典方法,按照缺乏一系列相关性来判断价格增量中不存在形态。 如果没有自相关,则将一系列增量视为随机的,且可相信进一步搜索形态是无效的。
我们来看一个利用自相关函数直观分析 EURUSD 增量的示例。 所有示例将运用 IPython 执行。
def standard_autocorrelation(symbol, lag):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
standard_autocorrelation('EURUSD', 50)
此函数将 H1 收盘价转换为指定周期的相关差额(所用为滞后 50),并显示自相关图表。
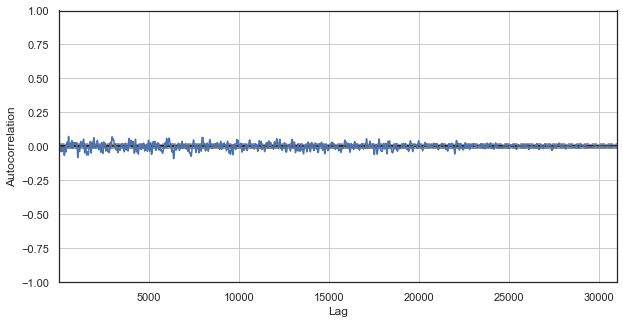
图例 1. 经典价格增量相关图
自相关图表不会揭示价格增里量的任何形态。 相邻增量之间的相关性在零附近波动,所指即为时间序列的随机性。 我们于此可终结计量经济学的分析,得出市场是随机的结论。 然而,我建议从不同的角度回顾自相关函数:与季节性形态关联的背景下。
我设想价格增量的相关性可能是由于存在季节性形态而产生的。 故此,我们从示例中把所有时段(特定时间除外)排除。 因之,我们将创建一个含有自己特定属性的新时间序列。 为这个序列构建一个自相关函数:
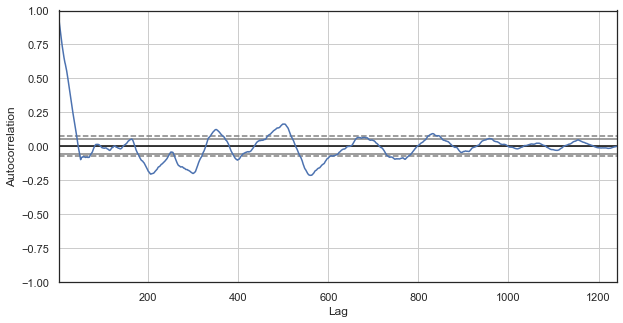
图例 2. 排除了时段的价格增量相关性图表(仅剩每天的第一小时)
新序列的相关图表观感更佳。 当前与以前的增量有更强的依赖关系。 当增量之间的时间差值递增时,依赖性降低。 这意味着当天的第一小时增量与前一天的第一小时增量紧密相关,依此类推。 这个非常重要的信息表明存在季节性形态,即增量具有记忆力。
我们已发现,当日的第一小时增量与前一日的第一小时增量之间存在相关性,不过若日间的距离递增时,该相关性会递减。 现在,我们查看相邻时段之间是否存在相关性。 为此,我们修改代码:
def seasonal_autocorrelation(symbol, lag, hour1, hour2):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
seasonal_autocorrelation('EURUSD', 50, 1, 2)
在此,删除第一和第二个之外的所有时段,然后计算新序列的差值,并构建自相关函数:
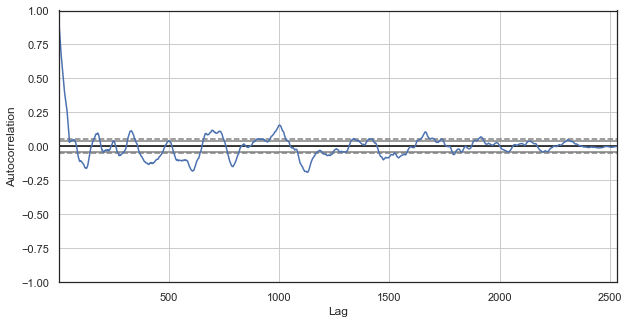
图例 3. 排除时段的价格增量相关性图表(仅剩每天的第一和第二个小时)
显而易见,最近的时段序列依然具有高度相关性,这表明它们之间有相关性,且相互影响。 我们能否可靠获取所有时段的相对分数,而不仅仅是选定的某一个? 为此,我们用到下面描述的方法。
我们来继续探索市场,并尝试确认原始设想。 我们在更高层面来观察。 下面的函数顺序从时间序列中删除时段,只剩一个时段。 它建立该系列的价格差值,并研判与依据其他时段所构建序列的相关性:
#calculate correlation heatmap between all hours def correlation_heatmap(symbol, lag, corrthresh): out = pd.DataFrame() rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') for i in range(24): ratesH = None ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna() out[str(i)] = ratesH['close'].reset_index(drop=True) plt.figure(figsize=(10, 10)) corr = out.corr() # Generate a mask for the upper triangle mask = np.zeros_like(corr, dtype=np.bool) mask[np.triu_indices_from(mask)] = True sns.heatmap(corr[corr >= corrthresh], mask=mask) return out out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)
该函数接受增量顺序(时间滞后),以及相关性阈值,低于该阈值的时段则被舍弃。 此为结果:

图例 4. 2015-2020 年间不同时段增量之间的相关性热点图。
很显然,以下集簇具有最大的相关性:0-5 和 10-14 时段。 在上一篇文章中,我们基于第一个集簇创建了一个交易系统,该集簇以不同的方式发现(借助箱线图)。 现在,这些形态在热点图上也可见。 现在,我们查看第二个有趣的集簇,并对其进行分析。 以下是集簇的摘要统计信息:
out[['10','11','12','13','14']].describe()
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 |
| mean | -0.001016 | -0.001015 | -0.001005 | -0.000992 | -0.000999 |
| std | 0.024613 | 0.024640 | 0.024578 | 0.024578 | 0.024511 |
| min | -0.082850 | -0.084550 | -0.086880 | -0.087510 | -0.087350 |
| 25% | -0.014970 | -0.015160 | -0.014660 | -0.014850 | -0.014820 |
| 50% | -0.000900 | -0.000860 | -0.001210 | -0.001350 | -0.001280 |
| 75% | 0.013460 | 0.013690 | 0.013760 | 0.014030 | 0.013690 |
| max | 0.082550 | 0.082920 | 0.085830 | 0.089030 | 0.086260 |
所有集簇时段的参数都非常接近,不过所分析样本的平均值为负数(若以五位小数为基准,则约 100 个点)。 平均增量的偏移表明,市场在这几个时段内暴跌的可能性大于上涨的可能性。 还值得注意的是,由于趋势分量的出现,增量滞后的递增会导致时段间的相关性更大,而滞后的递减会导致较低的值。 不过,集簇的相对排列几乎未变。
例如,对于单个滞后,时段 12、13 和 14 的增量仍然强烈相关:
plt.figure(figsize=(10,5)) plt.plot(out[['12','13','14']]) plt.legend(out[['12','13','14']]) plt.show()
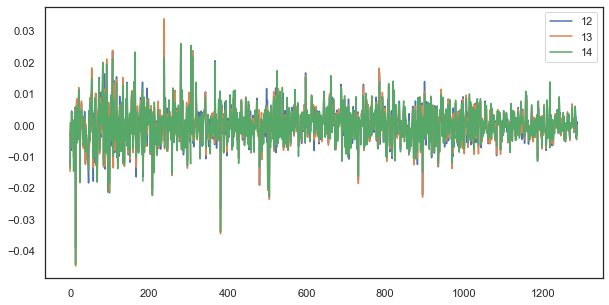
图例 5. 由不同时段组成的含有单个滞后的一系列增量之间的视觉相似性
记住设想:
价格增量的相关性取决于季节形态的存在,以及附近增量的集簇。 f
正如我们在自相关图和热点图上所见,时段增量依赖性与过去/近期时段的增量都相关。 第一种现象源于日内某些时段的事件会重复发生。 第二个现象与一定周期内的波动性集簇有关。 这两种现象应分开考虑,并在可能的情况下加以组合。 在本文中,我们将针对特定时段增量(从时间序列中删除所有其他时段)基于其前值的依赖性进行额外的研究。 该研究最有趣的部分将在下一篇文章中实施。
# calculate joinplot between real and predicted returns def hourly_signals_statistics(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') # price differences for every hour series H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna() H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna() # current returns for both hours HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True) # previous returns for both hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1]) # or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) predicted = HF-(HF2-HL2) real = HL # correlation joinplot between two series outcorr = pd.DataFrame() outcorr['Hour ' + str(hour)] = H['close'] outcorr['Hour ' + str(hour2)] = H2['close'] # real VS predicted prices out = pd.DataFrame() out['real'] = real['close'] out['predicted'] = predicted['close'] out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))] # plptting results from scipy import stats sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)
此为以上清单中所做所为的解释。 通过删除不必要的时段,形成了两个序列,基于计算出的价格增量(其差额)。 该序列的时段在 “hour” 和 “hour2” 参数中确定。 然后,我们获得每小时延迟为 1 的序列,即 HF 序列比 HL 领先一个值 — 这能够计算实际增量和预测增量,以及它们之间的差值。 首先,我们为第一个和第二个小时的增量构建一个散点图:
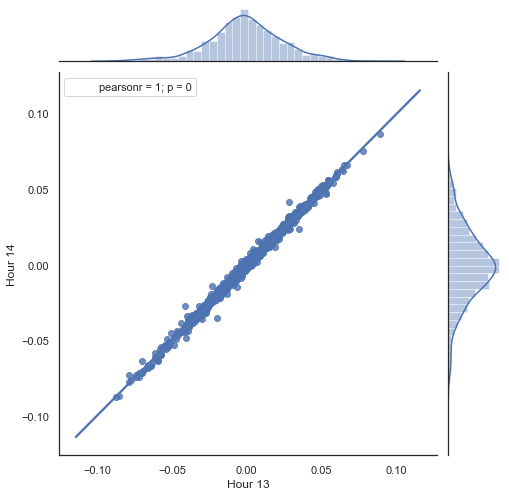
图例 5. 2015-2020 年间第 13 和 14 小时的增量散点图。
如预期的那样,增量高度相关。 现在,我们尝试根据前一个增量预测下一个增量。 为此,此处的一个简单公式,可以预测下一个值:
基本方程式: ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
或者 Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1]))
这是对所得公式的解释。 为了预测未来的增量,我们立于零号柱线上。 预测下一个增量的值ret [-1]。 为此,从当前增量中减去前一个增量(“lag”)和下一个增量(lag-1)之差。 如果两个相邻时段间的增量相关性很强,则能期待所预测增量可由该公式描述。 以下是针对收盘价的方程解释。 因此,未来的预测基于三个增量。 第二部分代码预测了将来的增量,并将其与实际增量进行比较。 此为图表:
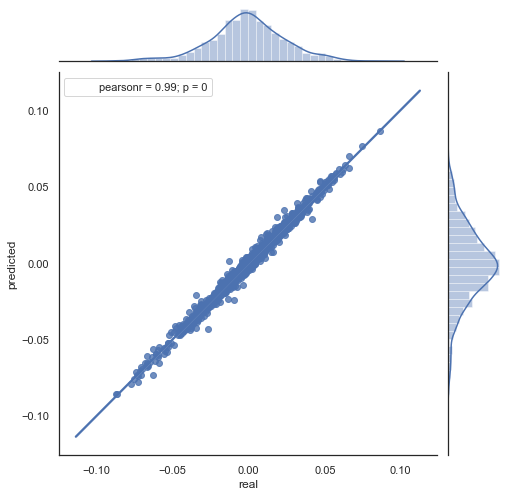
图例 6. 2015-2020 年间实际和预测增量的散点图。
您可以看到图例 5 和 6 中的图表相似。 这意味着通过相关性判断形态的方法足以胜任。 同时,数值散布在整个图表中;它们并不在同一条直线上。 这些是预测误差,会对预测产生负面影响。 它们应该分别处理(这超出了本文的讨论范围)。 零附近的预测并不是很有趣:如果下一个价格增量的预测等于当前值,则您无法从中获利。 可以利用 rfilter 参数过滤预测。
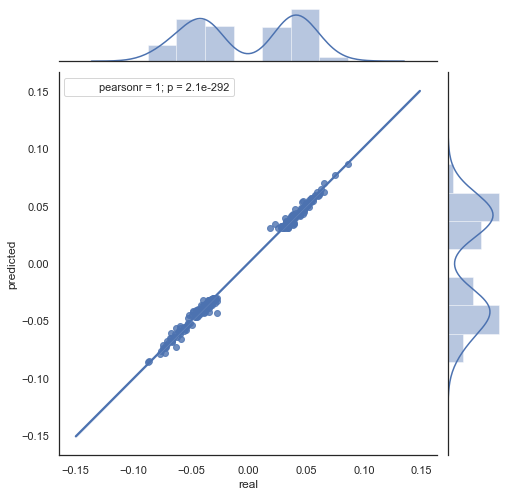
图例 7. 2015-2020 年间 rfilter = 0.03 的实际和预测增量散点图。
请注意,热点图是利用 2015 年到当前日期的数据创建的。 我们将偏移日期回退到 2000 年:
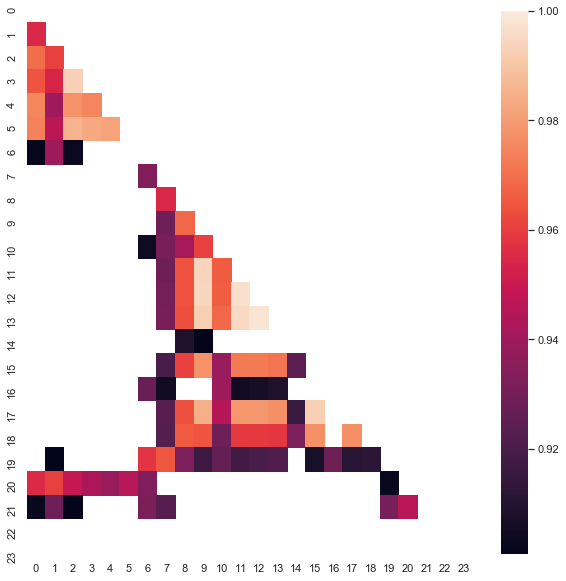
图例 8. 2000 年至 2020 年间不同时段增量之间的相关性热点图。
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 |
| mean | 0.000470 | 0.000470 | 0.000472 | 0.000472 | 0.000478 |
| std | 0.037784 | 0.037774 | 0.037732 | 0.037693 | 0.037699 |
| min | -0.221500 | -0.227600 | -0.222600 | -0.221100 | -0.216100 |
| 25% | -0.020500 | -0.020705 | -0.020800 | -0.020655 | -0.020600 |
| 50% | 0.000100 | 0.000100 | 0.000150 | 0.000100 | 0.000250 |
| 75% | 0.023500 | 0.023215 | 0.023500 | 0.023570 | 0.023420 |
| max | 0.213700 | 0.212200 | 0.210700 | 0.212600 | 0.208800 |
如您所见,热点图稍微变薄了,而 13 和 14 时段之间的依赖关系却有所减少。 同时,增量的平均值为正数,这为买入设定了更高的优先级。 平均值的偏移不允许在两个时段内进行有效交易,因此您必须选择。
我们看一下此期间的散点图(这里我只提供实际的\预测图):

图例 9. 2000 年至 2020 年间 rfilter = 0.03 的实际和预测增量的散点图。
数值的散布增加了,对于这么长的时间内,这是一个负面因素。
因此,我们获得了某些时段的实际增量和预测增量的分布公式和近似概念。 为了更加清晰,依赖性可在 3D 图中直观呈现。
# calculate joinplot between real an predicted returns def hourly_signals_statistics3D(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') rates = pd.DataFrame(rates['close'].diff(lag)).dropna() out = pd.DataFrame(); for i in range(hour, hour2): H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None; H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True) H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True) HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True); # current hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # last day hours predicted = HF-(HF2-HL2) real = HL out3D = pd.DataFrame() out3D['real'] = real['close'] out3D['predicted'] = predicted['close'] out3D['predictedABS'] = predicted['close'].abs() out3D['hour'] = i out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))] out = out.append(out3D) import plotly.express as px fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000) fig.show() hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)
该函数利用已知的公式来计算预测值和实际值。 每个单独的散点图显示每小时的实际/预测的依赖性,就好像在前一天的时段 100 增量处生成了信号一样。 以 10:00 到 23:00 时段为例。 相邻最近的时段之间相关性最大。 随着距离的增加,相关性减小(散点图变得更像圆形)。 从第 16 小时开始,其它时段相对前一天的 10 时几乎没有依赖性。 利用附件,您可以旋转 3D 对象,并选择片段,从而获得更多详细信息。
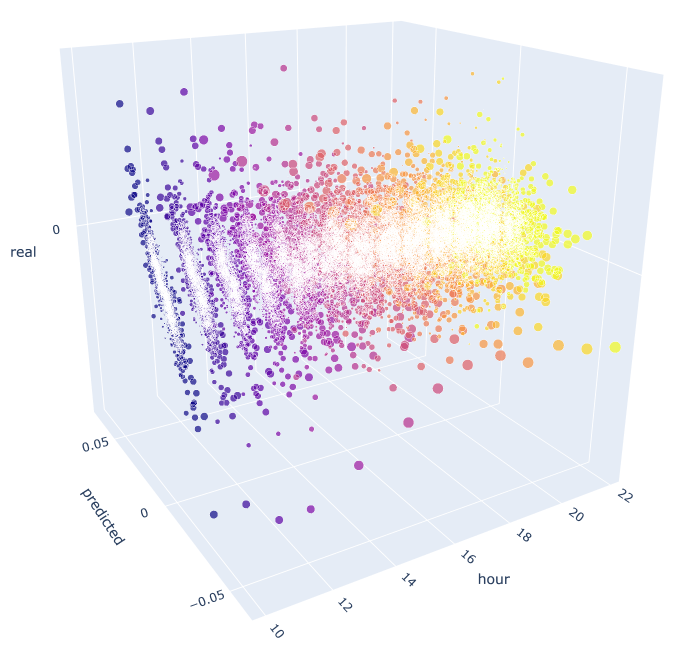
图例 10. 2015 年至 2020 年实际和预测增量的 3D 散点图。
现在是时候创建一个智能交易系统来查看其工作原理了。
与上一篇文章中的示例类似,该机器人仅依据某个特定时段当前与前一个增量之间的统计关系形成的季节性形态进行交易 。 区别在于,其它时段会运用基于提议的公式交易。
我们来研究一个基于统计的结果公式进行交易的示例:
input int OpenThreshold = 30; //Open threshold input int OpenThreshold1 = 30; //Open threshold 1 input int OpenThreshold2 = 30; //Open threshold 2 input int OpenThreshold3 = 30; //Open threshold 3 input int OpenThreshold4 = 30; //Open threshold 4 input int Lag = 10; input int stoploss = 150; //Stop loss input int OrderMagic = 666; //Orders magic input double MaximumRisk=0.01; //Maximum risk input double CustomLot=0; //Custom lot
检测到含有形态的间隔:{10、11、12、13、14}。 有基于此,可以分别为每时段设置 “Open threshold” 参数。 这些参数类似于图例 9 中的 “rfilter”。 `Lag' '变量包含增量的滞后值(请记住,默认情况下,我们分析的滞后为 25,即 H1 时间帧上的将近一天)。 可以为每个时段分别设置 Lag,但为简单起见,此处所有时段都采用相同的数值。 所有持仓的止损也相同。 所有这些参数都可以优化。
交易逻辑如下:
void OnTick() { //--- if(!isNewBar()) return; CopyClose(NULL, 0, 0, Lag*2+1, prArr); ArraySetAsSeries(prArr, true); const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1])); TimeToStruct(TimeCurrent(), hours); if(hours.hour >=10 && hours.hour <=14) { //if(countOrders(0)==0) // if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) // OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN); if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) { if(pr <= -signal && hours.hour==10) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic); if(pr <= -signal1 && hours.hour==11) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic); if(pr <= -signal2 && hours.hour==12) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic); if(pr <= -signal3 && hours.hour==13) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic); if(pr <= -signal4 && hours.hour==14) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic); } } }
“pr” 常数由上述指定公式计算得出。 该公式预测下一根柱线的价格增加。 然后检查每个时段的条件。 如果增量达到特定时段的最小阈值,则达成卖出。 我们已经发现,在 2015 年至 2020 年间,若平均增量转移到负数区域会令买入无效,您可自行检查这一点。
我们采用图例 11 中指定的参数启动遗传优化,并查看结果:
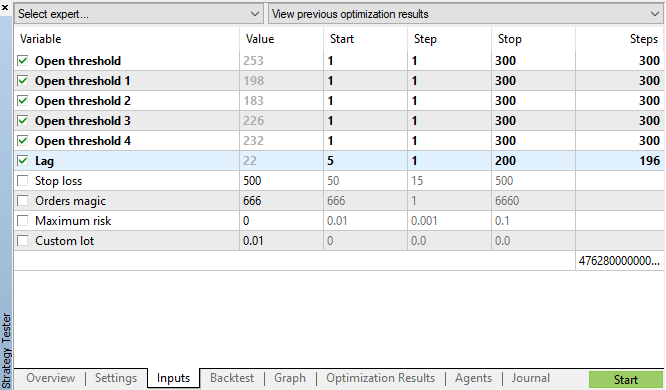
图例 11. 遗传优化参数表
我们查看一下优化图表。 在最优间隔中,最有效的滞后值位于 17-30 时段之间,这与我们的假设非常接近:当天特定时段的增量依赖于前一天同一时段:
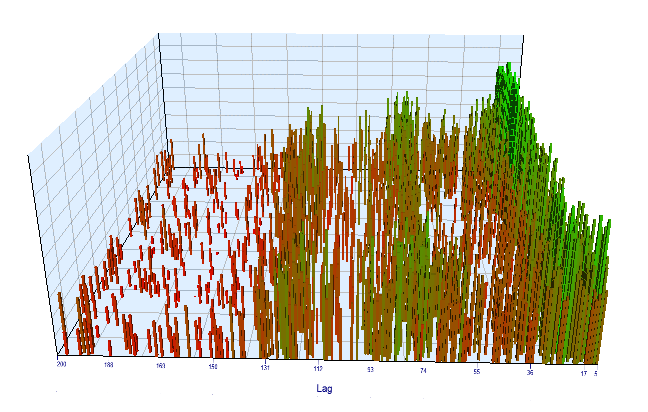
图例 12. 优化间隔中 “Lag” 变量与 “Order threshold” 变量的关系
正向图表看起来类似:
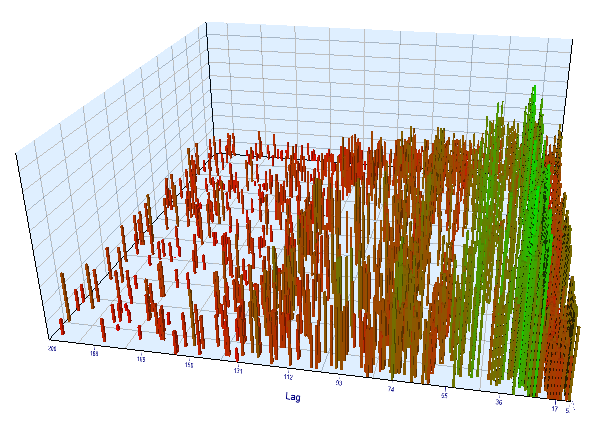
图例 13. 正向间隔中 “Lag” 变量与 “Order threshold” 变量的关系
此为来自复盘测试和正向优化表格的最佳结果:
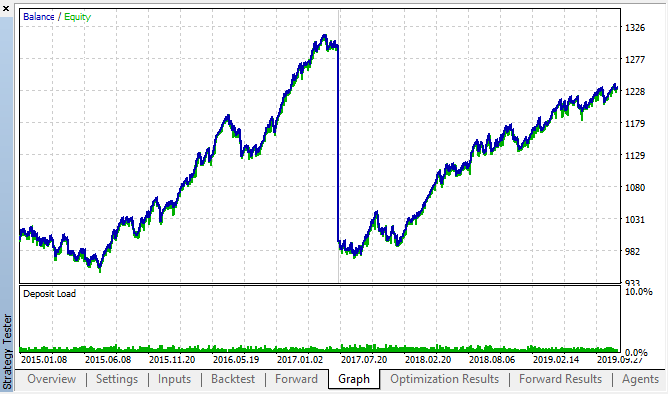
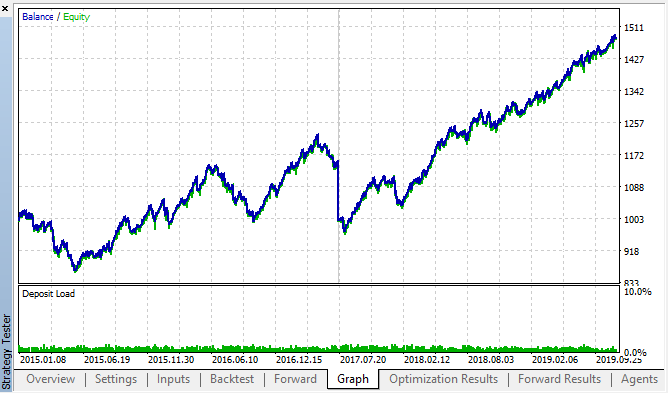
图例 14, 15. 复盘测试和正向优化图表
可以看出,这种形态在整个 2015–2020 年间持续存在。 我们可以假设计量经济学方法效果良好。 在一周的接下来几天中,同一时段的增量之间存在依赖关系,并且存在一些集簇(依赖关系可能不是同一时段,而是临近的时段)。 在下一篇文章中,我们将分析如何运用第二种形态。
我们在 M15 时间帧内执行附加检查。 假设我们正在当前时间和前一天的相同时段之间寻找相同的相关性。 在这种情况下,有效滞后必须大 4 倍,并且必须约为 24*4=96,因为每个小时包含四个 M15 周期。 我已经采用相同的设置和 M15 时间帧优化了智能交易系统。
在最佳间隔中,所得的有效滞后小于60,这很奇怪。 也许优化器找到了另一种形态,或者 EA 优化过度。
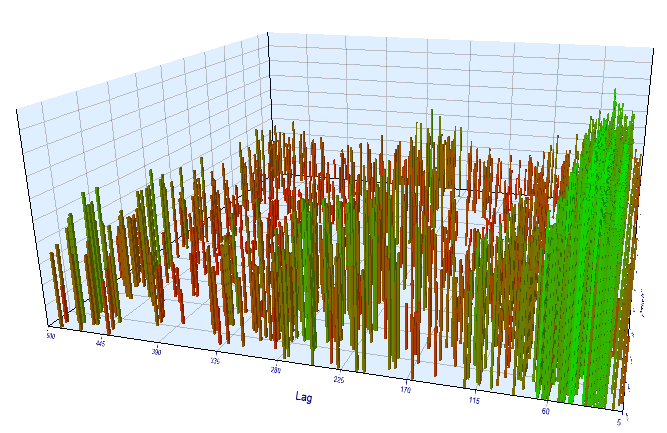
图例 16. 优化间隔中 “Lag” 变量与 “Order threshold” 变量的关系
至于正向测试结果,有效滞后是正常的,对应于 100,这可确认形态。
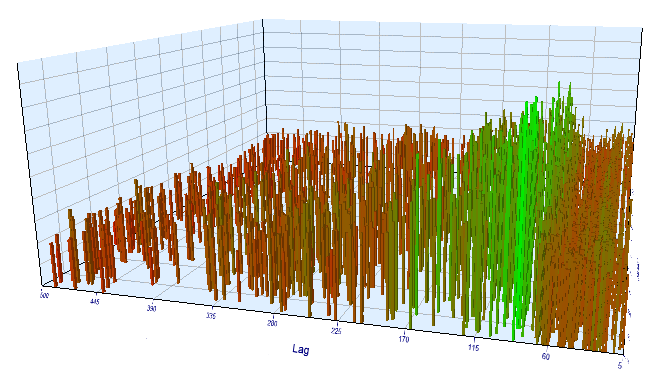
图例 17. 正向间隔中 “Lag” 变量与 “Order threshold” 变量的关系
我们查看最佳回测和正向结果:
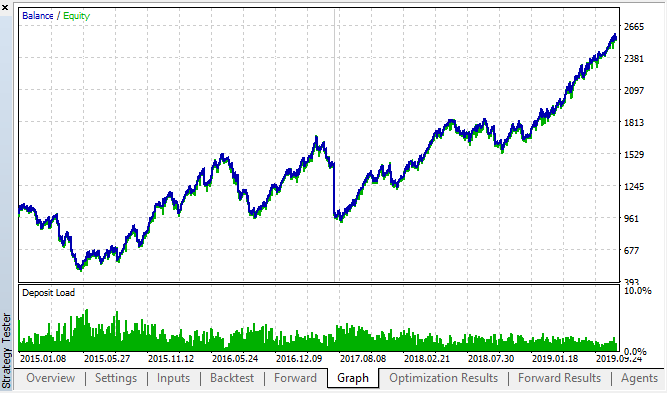
图例 18. 回测和正向; 最好的正向通关成绩
所得曲线类似于 H1 图表曲线,交易次数显著增加。 也许,该策略可在更低的时间帧里进行优化。
在本文中,我们提出以下设想:
价格增量的相关性取决于季节形态的存在,以及附近增量的集簇。
第一部分已完全得到确认:来自不同时间周的时段增量之间存在相关性。 第二个陈述已被隐式确认:相关性具有集簇性,这意味着当前时段增量还取决于相邻时段增量。
请注意,建议的智能交易系统绝不是依据所发现相关性进行交易的唯一可能变体。 所提出的逻辑反映了作者对相关性的看法,而 EA 优化只是为了进一步确认可由统计研究发现该形态。
由于我们研究的第二部分需要附加的实质性研究,因此在下一篇文章中,我们将利用一款简单的机器学习模型来完全该假设第二部分的确认或反驳。
附件包含现成的框架,保存为 Jupyter 笔记本格式,您可以利用该框架来研究其他金融工具。 利用随附的测试 EA 可进一步测试结果。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
