人工智能正在我们生活的各个方面提升覆盖面。 许多新刊物涌现,指出“神经网络已被训练为...”。然而,人工智能仍然伴随着奇妙的事物。 这个想法似乎非常复杂,超自然和玄之又玄。 所以,只有一群科学家才能创造出来这种超凡神迹。 利用我们的家用 PC 似乎无法开发类似的程序。 但请相信我,这并不困难。 我们尝试了解神经网络是什么,以及如何在交易中运用它。
维基百科如此定义神经网络:
人工神经网络(ANN)是受到构成动物大脑的生物神经网络的启发建立的计算系统。 ANN 基于称之为人工神经元的单元或节点连接而成的集合,可模拟生物大脑中的神经元耦合模型。
如此,神经网络是由人工神经元组成的实体,其相对关系有组织地编制。 这些关联类似于生物大脑。
下图展示了一个简单的神经网络示意图。 此处,圆圈表示神经元,且神经元之间直观地以线连接。 神经元被划分为三组,每组位于一层中。 蓝色表示神经元输入层,意即源信息输入。 绿色和红色是输出神经元,输出神经网络的运算结果。 它们之间是灰色神经元,形成隐藏层。
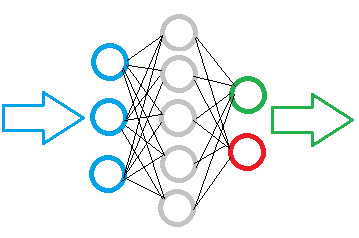
尽管划分了一些层,但整个网络是由相同的神经元构建的,输入信号可对应若干个元素,而结果仅对应一个元素。 输入数据在神经元内进行处理,然后输出简单的逻辑结果。 例如,可以为 “是” 或 “否”。 当应用于交易时,输出的结果可作为交易信号,或交易方向。
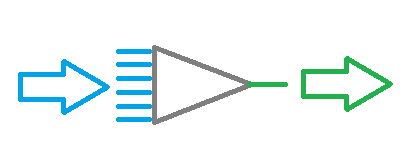
初始信息输进到神经元输入层,然后进行处理,处理后的结果作为下一层神经元的源信息。 逐层重复操作,直至到达输出层神经元为止。 因此,原始数据经逐层处理并过滤,最后生成结果。
取决于任务的复杂性和所创建模型,每一层中神经元的数量可以变化。 一些网络变体可能包括多个隐藏层。 这种更先进的神经网络可以解决更复杂的难题。 然而,这需要更多的计算资源。
因此,在创建神经网络模型时,必须定义要处理的数据体量和期望的结果。 这会影响模型层中所需神经元的数量。
如果我们需要将 10 个元素的数据数组输入到神经网络,则网络输入层应包含 10 个神经元。 如此即可接受数据数组的所有 10 个元素。 超出的输入神经元即是多余。
输出神经元的品质由期望的结果检验。 为了获得无歧义的逻辑结果,一个输出神经元就足够了。 如果您希望接收若干个问题的答案,请为每个问题创建一个神经元。
隐藏层充当分析中心,用于处理和分析接收到的信息。 因此,该层中神经元的数量取决于前一层数据的可变性,即每个神经元都代表某种事件的假设。
隐藏层的数量由源数据和预期结果之间的因果关系判定。 例如,如果我们希望为 “5 个为什么” 创建模型,则逻辑解决方案是使用 4 个隐藏层,这些隐藏层与输出层相配合可对源数据分解 5 个问题。
总结:
我们现已研究了神经网络的结构,我们来继续创建人工神经元模型。 所有的数学计算和决策制定都在该神经元内部执行。 此处会引发一个问题:我们如何才能基于相同的源数据以及运用相同的公式来实现众多不同的解决方案? 解决方案是改变神经元之间的连接。 为每个连接判定其权重系数。 此权重设定了输入值将对结果产生多少影响。
神经元的数学模型包含两个功能。 首先汇总输入数据与其权重系数的乘积。
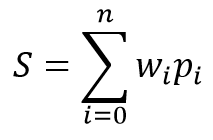
基于得到的数值,在所谓的激活(activation)函数中计算结果。 实际上,会用到激活函数的各种变体。 最常用的方法如下:
激活函数的选择取决于要解决的问题。 例如,如果我们期望源数据的处理结果是一个逻辑答案,则首选 sigmoid 函数。 对于交易目的,我更喜欢使用双曲正切。 数值 "-1" 对应于卖出信号,“1” 对应于买入信号。 中值结果代表不确定性。
如上所述,每个神经元和整个神经网络的可变性结果取决于神经元之间连接的所选权重。 权重选择问题称为神经网络学习。
可以按照各种算法和方法来训练网络:
学习方法取决于神经网络的源数据和任务集合。
当有足够的初始数据集合,且提出的问题有相应的正确答案时,会采用监督学习。 在学习过程中,将初始数据输入到网络中,并用已知的正确答案验证输出。 之后,调整权重来降低误差。
当存在一组初始数据而没有相应的正确答案时,会采用无监督学习。 在这种方法中,神经网络搜索相似的数据集合,并允许将源数据划分为相似的组。
在没有正确答案,但我们知晓所需结果的情况下,采用强化学习。 在学习过程中,源数据被输入到网络中,然后尝试解决该问题。 结果验证之后,发送反馈作为一定的奖励。 在学习期间,网络尝试得到最大的奖励。
在本文中,我们将采用监督学习。 举例,我采用向后反馈算法。 这种方法可以持续地实时训练神经网络。
该方法基于利用神经网络输出的误差来校正其权重。 学习算法由两个阶段构成。 首先,网络根据输入数据计算结果值,然后用参考值验证该数值,并计算误差。 接下来,执行逆向传递,将误差从网络输出端反馈到输入端,并调整所有权重因子。 这是一种交互式方法,网络可因此逐步得以训练。 利用历史数据学习后,可于在线模式下进一步对网络训练。
向后反馈方法采用随机阶梯下沉法,能达到可接受的最小误差。 以在线模式进一步训练网络能够在很长的时间段内维持该最低级别。
现在,我们进入本文的实施部分。 为了令神经网络(NN)操作更加直观,我们仅用 MQL5 语言创建示例,无需任何第三方函数库。 我们从创建存储有关神经元之间基本连接数据的类开始。
首先,创建 СConnection 类以便存储一个连接的权重系数。 它作为 CObject 类的子级创建。 该类将包含两个双精度类型变量:“weight” 存储权重,和 deltaWeight,其内我们会存储最后一次的变化权重值(在学习当中会用到)。 为避免调用额外方法来处理该变量,令它们作为公开变量。 在类构造函数中设置变量的初始值。
class СConnection : public CObject { public: double weight; double deltaWeight; СConnection(double w) { weight=w; deltaWeight=0; } ~СConnection(){}; //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); };
为了能够保存有关连接的更多信息,我们创建一个将数据保存到文件(Save),以及读取该数据的方法(Load)。 这些方法基于经典方案:在方法参数中接收文件句柄,然后验证之后将数据写入(或在 Load 方法中读取)。
bool СConnection::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(file_handle,weight)<=0) return false; if(FileWriteDouble(file_handle,deltaWeight)<=0) return false; //--- return true; }
下一步是创建一个存储权重的数组:基于 CArrayObj 的 CArrayCon。 此处,我们重写了两个虚方法,CreateElement 和 Type。 第一个创建新元素,第二个识别我们的类。
class CArrayCon : public CArrayObj { public: CArrayCon(void){}; ~CArrayCon(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7781); } };
在创建新元素的 CreateElement 方法的参数中,我们将传递此新元素的索引。 在方法里验证有效性,检查数据存储数组的大小,并在必要时调整大小。 然后创建 СConnection 类的新实例,并随机赋予初始权重。
bool CArrayCon::CreateElement(const int index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- m_data[index]=new СConnection(MathRand()/32767.0); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; m_data_total=MathMax(m_data_total,index); //--- return (true); }
下一步是创建人工神经元。 如早前所述,我采用双曲正切作为神经元的激活函数。 结果值的范围在 “-1” 和 “1” 之间。 "-1" 代表卖出信号,而 "1" 意即买入信号。
与先前的 CConnection 元素类似,CNeuron 人工神经元类继承自 CObject 类。 不过它的结构稍微复杂一些。
class CNeuron : public CObject { public: CNeuron(uint numOutputs,uint myIndex); ~CNeuron() {}; void setOutputVal(double val) { outputVal=val; } double getOutputVal() const { return outputVal; } void feedForward(const CArrayObj *&prevLayer); void calcOutputGradients(double targetVals); void calcHiddenGradients(const CArrayObj *&nextLayer); void updateInputWeights(CArrayObj *&prevLayer); //--- methods for working with files virtual bool Save(const int file_handle) { return(outputWeights.Save(file_handle)); } virtual bool Load(const int file_handle) { return(outputWeights.Load(file_handle)); } private: double eta; double alpha; static double activationFunction(double x); static double activationFunctionDerivative(double x); double sumDOW(const CArrayObj *&nextLayer) const; double outputVal; CArrayCon outputWeights; uint m_myIndex; double gradient; };
在类构造函数参数中,传递外向神经元连接数量,和层中神经元的序号(后续神经元识别时会用到)。 在方法主体中,设置常量,保存接收到的数据,并创建外向连接的数组。
CNeuron::CNeuron(uint numOutputs, uint myIndex) : eta(0.15), // net learning rate alpha(0.5) // momentum { for(uint c=0; c<numOutputs; c++) { outputWeights.CreateElement(c); } m_myIndex=myIndex; }
setOutputVal 和 getOutputVal 方法用于访问神经元的结果值。 神经元的结果值是在 feedForward 方法中计算的。 前一层神经元作为该方法的输入参数。
void CNeuron::feedForward(const CArrayObj *&prevLayer) { double sum=0.0; int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *temp=prevLayer.At(n); double val=temp.getOutputVal(); if(val!=0) { СConnection *con=temp.outputWeights.At(m_myIndex); sum+=val * con.weight; } } outputVal=activationFunction(sum); }
方法主体包含一个循环,可遍历所有上一层神经元。 结果神经元的值和权重的乘积,也在方法主体中汇总。 在计算出总和后,将由 activationFunction 方法计算得出神经元值(神经元激活函数作为单独方法予以实现)。
double CNeuron::activationFunction(double x) { //output range [-1.0..1.0] return tanh(x); }
下一个方法模块用于神经网络学习。 为激活函数创建一个计算导数的方法 ActivationFunctionDerivative。 这能判断求和函数中所需的变化,以便补偿结果神经元值的误差。
double CNeuron::activationFunctionDerivative(double x) { return 1/MathPow(cosh(x),2); }
接下来,创建两个调整权重的梯度计算方法。 我们需要创建两种方法,因为对于输出层和隐藏层的神经元,应以不同的方式计算结果值的误差。 对于输出层,误差计算是结果值与参考值之间的差值。 对于隐藏层神经元,误差计算则为:基于神经元之间的连接权重,与后一层所有神经元的梯度进行加权的总和。 计算作为单独的 sumDOW 方法实现。
void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer) { double dow=sumDOW(nextLayer); gradient=dow*CNeuron::activationFunctionDerivative(outputVal); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CNeuron::calcOutputGradients(double targetVals) { double delta=targetVals-outputVal; gradient=delta*CNeuron::activationFunctionDerivative(outputVal); }
然后将误差乘以激活函数的导数来判定梯度。
我们来详究 sumDOW 方法,该方法判定隐藏层的神经元误差。 该方法接收指向神经元下一层的指针作为参数。 在方法主体中,首先将结果值的合计 “sum” 清零,然后在循环里遍历下一层所有神经元,并将神经元的梯度与其连接权重的乘积求和。
double CNeuron::sumDOW(const CArrayObj *&nextLayer) const { double sum=0.0; int total=nextLayer.Total()-1; for(int n=0; n<total; n++) { СConnection *con=outputWeights.At(n); CNeuron *neuron=nextLayer.At(n); sum+=con.weight*neuron.gradient; } return sum; }
上述准备工作一旦完成后,我们只需创建 updateInputWeights 方法即可重新计算权重。 在我的模型中,神经元存储外向权重,因此权重更新方法在参数中接收神经元的上一层。
void CNeuron::updateInputWeights(CArrayObj *&prevLayer) { int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); СConnection *con=neuron.outputWeights.At(m_myIndex); con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight; } }
方法主体包含一个循环遍历上一层所有神经元,权重调整则表示对当前神经元的影响。
请注意,权重调整依据两个系数执行:eta(当前导数降低反应)和 alpha(惯性系数)。 这种方式可将许多后续学习的迭代影响进行一定的平均,并可滤除噪音数据。
创建人工神经元后,我们需要将所创建的对象合并到单个实体当中,即神经网络。 结果对象必须灵活,且必须允许创建不同配置的神经网络。 这令我们能够在各种任务里采用生成的解决方案。
如上所述,神经网络由层次化神经元组成。 所以,第一步是将神经元合并为一层。 我们来创建 CLayer 类。 其中的基本方法是自 CArrayObj 继承而来。
class CLayer: public CArrayObj { private: uint iOutputs; public: CLayer(const int outputs=0) { iOutputs=outpus; }; ~CLayer(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7779); } };
在 CLayer 类初始化方法的参数中,设置下一层的元素数量。 另外,我们重写两个虚方法:CreateElement(创建该层的新神经元)和 Type(对象识别方法)。
创建新神经元时,请在方法参数中指定其索引。 在方法主体中检查收到的索引有效性。 然后检查数组的大小,以便存储指向神经元对象实例的指针,并在必要时增加数组的大小。 之后,创建神经元。 如果成功创建新的神经元实例,则设置其初始值,并更改数组中的对象数量。 然后以 “true” 退出该方法。
bool CLayer::CreateElement(const uint index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CNeuron *neuron=new CNeuron(iOutputs,index); if(!CheckPointer(neuron)!=POINTER_INVALID) return false; neuron.setOutputVal((neuronNum%3)-1) //--- m_data[index]=neuron; m_data_total=MathMax(m_data_total,index); //--- return (true); }
按照类似的方法,创建 CArrayLayer 类存储指向我们网络层的指针。
class CArrayLayer : public CArrayObj { public: CArrayLayer(void){}; ~CArrayLayer(void){}; //--- virtual bool CreateElement(const uint neurons, const uint outputs); virtual int Type(void) const { return(0x7780); } };
与前一个类的区别在于 CreateElement 方法,该方法创建一个新的数组元素。 在此方法参数中,指定要创建的当前层和其他层中神经元的数量。 在方法主体中,检查层中神经元的数量。 如果在所创建的层中没有神经元,则以 “false” 退出。 然后检查是否有必要调整存储指针数组的大小。 之后,可以创建对象实例:创建一个新层,并实现一个循环来创建神经元。 检查每一步中所创建的对象。 如果发生错误,则以 “false” 值退出。 创建所有元素后,在数组中保存指向所创建层的指针,并以 “true” 退出。
bool CArrayLayer::CreateElement(const uint neurons, const uint outputs) { if(neurons<=0) return false; //--- if(m_data_max<=m_data_total) { if(ArrayResize(m_data,m_data_total+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CLayer *layer=new CLayer(outputs); if(!CheckPointer(layer)!=POINTER_INVALID) return false; for(uint i=0; i<neurons; i++) if(!layer.CreatElement(i)) return false; //--- m_data[m_data_total]=layer; m_data_total++; //--- return (true); }
为层和层的数组创建单独的类,以便能够创建不同配置的各种神经网络,而无需修改类。 这是一个灵活的实例,允许输入所需数量的层,意即每层的神经元。
现在,我们来研究创建神经网络的 CNet 类。
class CNet { public: CNet(const CArrayInt *topology); ~CNet(){}; void feedForward(const CArrayDouble *inputVals); void backProp(const CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals); double getRecentAverageError() const { return recentAverageError; } bool Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; private: CArrayLayer layers; double recentAverageError; };
在上述类中,我们已经实现了很多必需的工作,因此神经网络类本身仅包含最少的变量和方法。 该类的代码仅包含两个用于计算和存储平均误差的统计变量(recentAverageSmoothingFactor 和 recentAverageError),以及指向包含网络层的 “layers” 数组指针。
我们来研究该类的方法的细节。 在类构造函数的参数中传递指向 int 数据数组的指针。 数组中的元素数量表示层数,而数组中的每个元素都包含相应层里的神经元数量。 因此,这个通用类可用于创建任何级别复杂度的神经网络。
CNet::CNet(const CArrayInt *topology) { if(CheckPointer(topology)==POINTER_INVALID) return; //--- int numLayers=topology.Total(); for(int layerNum=0; layerNum<numLayers; layerNum++) { uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1)); if(!layers.CreateElement(topology.At(layerNum), numOutputs)) return; } }
在方法主体中,检查所传递指针的有效性,并实现循环来创建神经网络中的层。 外向连接值为零代表输出层。
feedForward 方法计算神经网络值。 在参数中,该方法接收基于计算神经网络的结果值计算得出的输入值数组。
void CNet::feedForward(const CArrayDouble *inputVals) { if(CheckPointer(inputVals)==POINTER_INVALID) return; //--- CLayer *Layer=layers.At(0); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=inputVals.Total(); if(total!=Layer.Total()-1) return; //--- for(int i=0; i<total && !IsStopped(); i++) { CNeuron *neuron=Layer.At(i); neuron.setOutputVal(inputVals.At(i)); } //--- total=layers.Total(); for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) { CArrayObj *prevLayer = layers.At(layerNum - 1); CArrayObj *currLayer = layers.At(layerNum); int t=currLayer.Total()-1; for(int n=0; n<t && !IsStopped(); n++) { CNeuron *neuron=currLayer.At(n); neuron.feedForward(prevLayer); } } }
在方法主体中,检查所接收指针和网络零层指针的有效性。 然后,将接收到的初始值设置为零层神经元的结果值,并实现一个双重循环,从第一隐藏层到输出神经元,阶段性重新计算整个神经网络中的神经元结果值。
利用 getResults 方法得到结果,该方法包含一个循环,收集来自输出层神经元的结果值。
void CNet::getResults(CArrayDouble *&resultVals) { if(CheckPointer(resultVals)==POINTER_INVALID) { resultVals=new CArrayDouble(); } resultVals.Clear(); CArrayObj *Layer=layers.At(layers.Total()-1); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=Layer.Total()-1; for(int n=0; n<total; n++) { CNeuron *neuron=Layer.At(n); resultVals.Add(neuron.getOutputVal()); } }
神经网络学习过程是在 backProp 方法中实现的。 该方法接收参数中的数值数组引用。 在方法主体中,检查接收到的数组的有效性,并计算结果层的均方误差。 然后,在循环中重新计算所有层的神经元的梯度。 之后,在最后一个方法层中,根据较早计算出的梯度更新神经元之间的连接权重。
void CNet::backProp(const CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return; CArrayObj *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double delta=targetVals[n]-neuron.getOutputVal(); error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; //--- for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); neuron.calcOutputGradients(targetVals.At(n)); } //--- for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CArrayObj *hiddenLayer=layers.At(layerNum); CArrayObj *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped();++n) { CNeuron *neuron=hiddenLayer.At(n); neuron.calcHiddenGradients(nextLayer); } } //--- for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CArrayObj *layer=layers.At(layerNum); CArrayObj *prevLayer=layers.At(layerNum-1); total=layer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=layer.At(n); neuron.updateInputWeights(prevLayer); } } }
为了避免在程序重新启动时再次训练系统,我们创建保存数据到本地文件的 “Save” 方法,和从文件中加载已保存数据的 “Load” 方法。
附件中提供了所有类方法的完整代码。
本文的目的是展示如何在家中创建神经网络。 当然,这只是冰山之一角。 本文所研究的仅是可能的一个版本,即感知器,它是由 Frank Rosenblatt 于1957 年引入的。 自该模型引入以来已有 60 多年的历史,并且出现了许多其他模型。 不过,感知器模型仍然可行,并产生了良好的结果 — 您可以自行测试该模型。 那些想深入了解人工智能概念的人应该阅读相关资料,因为即使占用一系列的篇幅,也无法涵盖所有内容。
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | NeuroNet.mqh | 类库 | 创建神经网络(感知器)的类库 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
