本文是有关 OpenCL 或开放运算语言编程系列短篇出版物中的第一篇。在提供对于 OpenCL 的支持之前,当前形式的 MetaTrader 5 平台并不允许直接(即以原生方式)享用多核处理器加速运算的优势。
显然,开发人员可以一直重复表示”此终端为多线程“以及“每个 EA/脚本均在独立线程中运行”,但编码人员却没有机会来相对简单地并行执行下述简单循环(一个计算 pi 值 = 3.14159265... 的代码):
long num_steps = 1000000000; double step = 1.0 / num_steps; double x, pi, sum = 0.0; for (long i = 0; i<num_steps; i++) { x = (i + 0.5)*step; sum += 4.0/(1.0 + x*x); } pi = sum*step;
然而,早在 18 个月以前,在 "Articles" 部分即有一篇名为《MetaTrader 5 中的并行计算》的趣文问世。不过,这篇文章给人的印象却是:尽管该方法设计精巧,但却有些不自然 - 上述循环中为加快运算而编写的整个程序层次结构(EA 交易和两个指标)可能会适得其反。
我们已经了解并没有支持 OpenMP 的计划,而且也清楚添加 OMP 需要对编译器进行大刀阔斧的重新编程。唉,难道就没有易于学习、简单实惠的代码解决方案吗?
因此,原生支持 МQL5 中 OpenCL 的消息一经公布,就受到了热烈欢迎。从同一新闻跟帖的第 22 页起,MetaDriver 就开始发布允许评估 CPU 与 GPU 上的实现差异的脚本。一时间,OpenCL 引起了广泛关注。
本文作者一开始决定对上述现象不予关注。极为低端的计算机配置(奔腾 G840/8 Gb DDR-III 1333/无显卡)似乎无法实现对 OpenCL 的有效利用。
不过,在安装 AMD APP SDK(AMD 加速并行运算软件开发套件)后,一款由 AMD 开发的专业软件(首个脚本由 MetaDriver 提出,且仅在独立显卡可用时才可运行)在作者的计算机中成功运行,并且与单核处理器上的标准脚本运行时间相比,其速度提升远非微不足道,而是足足快了约 25 倍!后来,由于在支持团队的协助下成功安装了 Intel OpenCL Runtime,同一脚本的运行时间更是快到了 75 倍。
仔细研究 ixbt.com 论坛及网站上的资料后,作者发现 Intel 的集成图形处理器 (IGP) 支持 OpenCL 1.1,但仅适用于 Ivy Bridge 处理器及以上版本的处理器。这样一来,在采用上述配置的 PC 中实现的加速便不可能与 IGP 有关,而在此特定情况下,OpenCL 程序代码就只能在 х86 核心的 CPU 上执行。
当作者与 ixbt.com 网站的专家共同研究加速数据后,他们立即做出了答复:这一切实际上都是源语言 (MQL5) 优化不足而造成的。在 OpenCL 专业人员群体中,众所周知,如果对 С++ 语言中的源代码进行了正确优化(当然前提是使用某种多核处理器和 SSEx 向量指令),则在最佳状态下能够使 OpenCL 仿真效果提升几十个百分点;而在最糟糕的情况下,甚至会出现数据丢失的现象(比如数据传输花费了过多<时间>)。
因此便出现了另一种假设:应充分重视 MetaTrader 5 中 OpenCL 完全仿真的“不可思议的”加速数据,而不是将其归因于 OpenCL 本身的出色。要发挥 С++ 程序中某个合理优化过的 GPU 的强大优势,只能通过一块功能极为强大的独立显卡来实现,因为其在某些算法中的计算能力远远超出了目前任何 CPU 的能力。
据此终端的开发人员称,其还未能实现合理优化。他们还暗示,优化后的加速程度会有数倍提升。而 OpenCL 中的加速数据也会相应减少“数倍”之多。但是,它们仍会远大于一。
这是学习 OpenCL 语言的不错理由(即便您的显卡不支持 OpenCL 1.1 或完全没有显卡),我们将谈到这一方面。不过首先,我还要简单讲讲必要的基础知识,那就是支持 Open CL 的软件及相应硬件。
1.1.AMD
相应的软件分别由 AMD、Intel 和 NVidia 提供,三家公司均为 Khronos 集团的成员;Khronos 集团为非营利性行业协会成员,负责制定与异构环境中的计算相关的不同语言规范。
Khronos 集团官网提供了一些有用资料,例如:
在学习 OpenCL 的过程中经常会用到这些文档,因为该终端并未提供与 OpenCL 相关的任何帮助信息(仅提供了一段 OpenCL API 摘要)。上述三家公司(AMD、Intel 和 NVidia)都是视频硬件供应商,每一家都有自己的 OpenCL 运行时实现和各自的软件开发工具包 - SDK。我们以 AMD 产品为例,深入讲解一下显卡选择的一些特性。
如果您的 AMD 显卡不是特别旧(2009-2010 年或以后首发),那就很简单了 - 只需升级一下显卡,就足以立即发挥功效了。OpenCL 兼容显卡列表请参见此处。另一方面,即便是当时还挺不错的显卡,比如 Radeon HD 4850 (4870),在处理 OpenCL 时也是麻烦多多。
如果您还没有 AMD 显卡,但特别想添加的话,那么请首先查看其规格。您可以在这里看到一个相当全面的 《最新 AMD 显卡规格表》。以下是最重要的注意事项:
现在来看下第二种情况:没有显卡,或是现有显卡不支持 OpenCL 1.1,而您却配有一个 AMD 处理器。您可以在此下载包含了运行时间以及 SDK、内核分析器和效能评测器的 AMD APP SDK。安装 AMD APP SDK 后,处理器就会被识别为一台 OpenCL 设备。而且,您还将能够在 CPU 仿真模式下开发功能完善的 OpenCL 应用程序。
与 AMD 不同,SDK 的主要特征在于其也可兼容 Intel 处理器(虽然在 Intel CPU 上开发时,原生 SDK 还会明显更加高效,因为其支持最近才可用于 AMD 处理器的 SSE4.1、SSE4.2 和 AVX 指令集)。
1.2. Intel
开始使用 Intel 处理器前,最好先下载 Intel OpenCL SDK/Runtime。
我们必须指出以下方面:
说实话,有关 Intel 的 OpenCL 支持的问题尚未得到完全解决,所以我们期望该终端的开发人员将来能给出一些解释。基本上,关键在于没有人会去为您关注内核代码错误(OpenCL 内核是一个在 GPU 上执行的程序) - 它可不是 MQL5 编译器。编译器只会取入一整行的内核,然后再尝试运行它。举个例子,比如您未声明内核中使用的某内部变量 х,该内核仍会严格执行,就会有错误也一样。
但是,您将在终端内获取的所有错误,归结之后也就十来个,其中有些已于 CLKernelCreate() 和 CLProgramCreate() 函数的 API OpenCL 相关帮助中有所描述。语言语法与 C 语言非常相似,并通过向量函数和数据类型得以增强(实际上,该语言是 1999 年被作为 ANSI C 标准采用的 C99)。
作者调试 OpenCL 代码时,使用的是 Intel OpenCL SDK 离线编译器;它比盲目地在 MetaEditor 中寻找内核错误方便太多了。希望以后的情况会变得更好。
1.3. NVidia
遗憾的是,作者并未搜索这一主题的相关信息。不过一般性建议仍是一样的。新款 NVidia 显卡的驱动程序会自动支持 OpenCL。
基本上,作者对 NVidia 显卡并没有什么异议,但根据查找到的信息和论坛讨论中获取到的知识,得出了如下结论:对于非图形运算而言,AMD 显卡似乎在性价比方面优于 NVidia 显卡。
现在我们来谈下编程。
要开发首款简单程序,我们需要这样来定义任务。在并行程序设计的过程当中,必须习惯使用 pi 值的计算结果(比如约等于 3.14159265)。
为此,应采用下述公式(作者之前从未见过这种特殊的公式,但它似乎是真的):
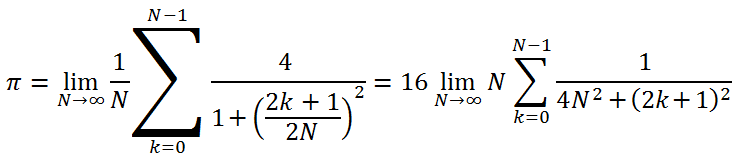
我们想将该值的计算结果精确到 12 个小数位。基本上,可利用 100 万次左右的迭代来实现该精度,但这个数字不会赋予我们评估在 OpenCL 中运算优点的能力,因为 GPU 上运算的持续时间太短了。
进行 GPGPU 编程时建议选择相应的运算量,以便让 GPU 任务至少持续 20 毫秒。在本例中,由于 GetTickCount() 函数与 100 ms 相比存在明显误差,所以该限制值要设置得更高一些。
下面是用于实现本运算的 MQL5 程序:
//+------------------------------------------------------------------+ //| pi.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" long _num_steps = 1000000000; long _divisor = 40000; double _step = 1.0 / _num_steps; long _intrnCnt = _num_steps / _divisor; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { uint start,stop; double x,pi,sum=0.0; start=GetTickCount(); //--- first option - direct calculation for(long i=0; i<_num_steps; i++) { x=(i+0.5)*_step; sum+=4.0/(1.+x*x); } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); //--- calculate using the second option start=GetTickCount(); sum=0.; long divisor=40000; long internalCnt=_num_steps/divisor; double partsum=0.; for(long i=0; i<divisor; i++) { partsum=0.; for(long j=i*internalCnt; j<(i+1)*internalCnt; j++) { x=(j+0.5)*_step; partsum+=4.0/(1.+x*x); } sum+=partsum; } pi=sum*_step; stop=GetTickCount(); Print("The value of PI is "+DoubleToString(pi,12)); Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds"); Print("_______________________________________________"); return(0); } //+------------------------------------------------------------------+编译并运行此脚本后,我们得到以下结果:
2012.05.03 02:02:23 pi (EURUSD,H1) The time to calculate PI was 8.783 seconds 2012.05.03 02:02:23 pi (EURUSD,H1) The value of PI is 3.141592653590 2012.05.03 02:02:15 pi (EURUSD,H1) The time to calculate PI was 7.940 seconds 2012.05.03 02:02:15 pi (EURUSD,H1) The value of PI is 3.141592653590
pi 值 ~ 3.14159265 以两种稍微不同的方式来计算。
第一种几乎可以说是证明具有多线程库(如 OpenMP、Intel TPP、Intel MKL 等)能力的一种经典方法。
第二种则是相同的计算,只不过采用了双循环的形式。由 10 亿次迭代构成的整个计算过程被分解成几个大型的外层循环块(其中包含了 40000 次迭代),而每个循环块都会执行 25000 次构成内部循环的“基本”迭代。
可以看出,此次运算的运行慢了 10-15%。但是,转换为 OpenCL 时,我们就打算将这种特定计算作为基础。主要原因在于选择了内核(GPU 上进行的基本计算任务),这样便在将数据从一个存储区域传输到另一存储区域所花的时间与照此运行内核中的计算量之间实现了一个合理的折衷。由此,就当前任务而言,一般来说,该内核将成为第二种计算算法的内部循环。
现在,我们利用 OpenCL 来计算该值。一份完整程序代码的后面会是绑定在 OpenCL 上的宿主语言 (MQL5) 函数特征的相关简短说明。但是首先,我想强调与可能会干扰 OpenCL 中编码的典型“障碍”相关的几个要点:
这里就是带有 OpenCL 内核的脚本代码:
//+------------------------------------------------------------------+ //| OCL_pi_float.mq5 | //+------------------------------------------------------------------+ #property copyright "Copyright (c) 2012, Mthmt" #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs; input int _device=0; /// OpenCL device number (0, I have CPU) #define _num_steps 1000000000 #define _divisor 40000 #define _step 1.0 / _num_steps #define _intrnCnt _num_steps / _divisor string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(int arg) { return IntegerToString(arg); } const string clSrc= "#define _step "+d2s(_step,12)+" \r\n" "#define _intrnCnt "+i2s(_intrnCnt)+" \r\n" " \r\n" "__kernel void pi( __global float *out ) \r\n" // type float "{ \r\n" " int i = get_global_id( 0 ); \r\n" " float partsum = 0.0; \r\n" // type float " float x = 0.0; \r\n" // type float " long from = i * _intrnCnt; \r\n" " long to = from + _intrnCnt; \r\n" " for( long j = from; j < to; j ++ ) \r\n" " { \r\n" " x = ( j + 0.5 ) * _step; \r\n" " partsum += 4.0 / ( 1. + x * x ); \r\n" " } \r\n" " out[ i ] = partsum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart() { Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt)); int clCtx=CLContextCreate(_device); int clPrg = CLProgramCreate( clCtx, clSrc ); int clKrn = CLKernelCreate( clPrg, "pi" ); uint st=GetTickCount(); int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float CLSetKernelArgMem(clKrn,0,clMem); const uint offs[ 1 ] = { 0 }; const uint works[ 1 ] = { _divisor }; bool ex=CLExecute(clKrn,1,offs,works); //--- Print( "CL program executed: " + ex ); float buf[]; // type float ArrayResize(buf,_divisor); uint read=CLBufferRead(clMem,buf); Print("read = "+i2s(read)+" elements"); float sum=0.0; // type float for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt]; float pi=float(sum*_step); // type float Print("pi = "+d2s(pi,12)); CLBufferFree(clMem); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); double gone=(GetTickCount()-st)/1000.; Print("OpenCl: gone = "+d2s(gone,3)+" sec."); Print("________________________"); return(0); } //+------------------------------------------------------------------+
稍后会更对脚本代码进行更为详细的阐述。
同时编译并启动程序,以获取下述内容:
2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) ________________________ 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) OpenCl: gone = 5.538 sec. 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) pi = 3.141622066498 2012.05.03 02:20:20 OCl_pi_float (EURUSD,H1) read = 40000 elements 2012.05.03 02:20:15 OCl_pi_float (EURUSD,H1) FLOAT: _step = 0.000000001000; _intrnCnt = 25000
可以看出,运行时间略有缩短。但我们还不能满足于此:其 pi 值约等于 3.14159265,明显只精确到了小数点后 3 位。该计算之所以不精确,是因为在实际运算中,内核采用的是精确度明显低于所要求 12 个小数位的浮点型数据。
根据 MQL5 文档,浮点型数据的精度仅为 7 个有效位数。而双精度类型的数据精度则会达到 15 个有效位数。
因此,我们需要让实际数据类型“更加精确”。在上述代码中,要用双精度类型替换的浮点类型数据所在行都会标以注释——///浮点型。利用相同的输入数据编译后,我们会获得下述内容(带源代码的新文件 - OCL_pi_double.mq5):
2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) OpenCl: gone = 12.480 sec. 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:25:35 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.03 03:25:23 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
运行时间大幅增加,甚至超过了运行不含 OpenCL 的源代码的时间(8.783 秒)。
“很明显,是双精度型拖慢了计算速度”,您可能会这么想。不过,让我们来试下对输入参数 _divisor 进行大幅修改,将其从 40000 改成 40000000:
2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) OpenCl: gone = 5.070 sec. 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.03 03:26:55 OCL_pi_double (EURUSD,H1) read = 40000000 elements 2012.05.03 03:26:50 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25
这样做并未影响到精度,而且运行时间还比浮点型情况下的时间稍短一些。但是,如果我们只是将所有整型从”长整型“改为“整型”,并恢复此前值 _divisor = 40000,则内核运行时间会降至一半:
2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) ________________________ 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) OpenCl: gone = 2.262 sec. 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) pi = 3.141592653590 2012.05.16 00:22:46 OCL_pi_double (EURUSD,H1) read = 40000 elements 2012.05.16 00:22:44 OCL_pi_double (EURUSD,H1) DOUBLE: _step = 0.000000001000; _intrnCnt = 25000
您始终都要记住:如果有一个相当“长”却“轻”的循环(即由大量迭代构成,而其中每个又都没有多少运算的循环),则只需将数据类型从 "重"(长型 - 8 字节)改为 "轻"(整型 - 4 字节)即可大幅缩短内核运行时间。
现在,我们暂时停下编程试验,专注于内核代码整体“绑定”的含义,以便对我们要做的工作有一些认知。我们暂且用内核代码“绑定”来指代 OpenCL API,即一个允许内核与主程序(本例中为 MQL5 中的程序)进行通信的指令系统。
3.1. 创建上下文
下面给出一个创建上下文的命令,即一个用于管理 OpenCL 对象和资源的环境。
int clCtx = CLContextCreate( _device );
首先,简单介绍下这种平台模型。
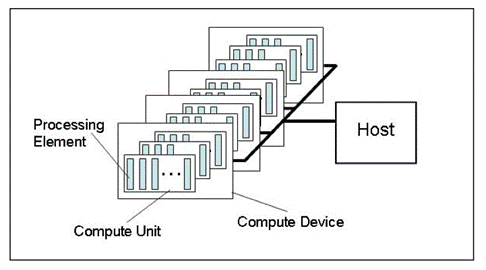
图 1. 某运算平台的抽象模型
此图所示为某运算平台的一个抽象模型。它对显卡相关硬件结构的描述还不够特别详细,但非常贴近真实,总体思路还不错。
主机为控制整个程序执行进程的主 CPU。它可以识别出几种 OpenCL 设备(计算设备)。在大多数情况下,如果交易者在系统单元中配备了用于计算的显卡,则显卡会被视为一个设备(而双处理器显卡则会被视为两个设备!)。此外,主机本身(即 CPU)始终被视为一个 OpenCL 设备。平台内的每个设备都有独一无二的编号。
如果设备中配备了对应 х86 核心的 CPU(其中包括 Intel CPU “虚拟”核心,即通过超线程技术创建的“核心”),则每个设备中都会配备多个计算单元;对于显卡而言,则会是 SIMD Engine (单指令多数据引擎),即遵守 《GPU 计算。AMD/ATI Radeon 架构特征》条款的 SIMD 核心与微处理器。功能强大的显卡通常有 20 个左右的 SIMD 核心。
每个 SIMD 核心都包含了流处理器,比如说,Radeon HD 5870 显卡的每个 SIMD 引擎中都有 16 个流处理器。
最终,每个流处理器都含有 4 到 5 个处理部件,即同一显卡中的 ALU(算数逻辑单元)。
要注意的是:所有主要图形硬件供应商使用的术语相当混乱,对于新人来说,就更是如此。"bees" 这样一个常用于 OpenCL 相关论坛跟帖中的词,其含义也不是始终明了。然而,线程数量(即如今显卡中计算的同步线程)非常庞大。比如说,Radeon HD 5870 显卡中的估算线程数量就有 5000 个之多。
下图所示为该显卡的标准技术规格。

图 2. Radeon HD 5870 GPU 特性
下面进一步指定的一切(OpenCL 资源)都有必要与通过 CLContextCreate() 函数创建的上下文进行关联:
所创建的上下文可描述为一个空字段,在其下方填上设备名称。
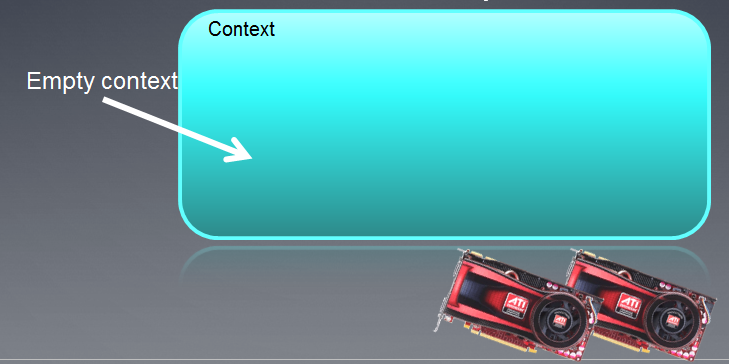
图 3. OpenCL 上下文
函数执行后,上下文字段目前为空。
要注意的是,MQL5 中的 OpenCL 上下文只用于处理一个设备。
3.2. 创建程序
int clPrg = CLProgramCreate( clCtx, clSrc );
CLProgramCreate() 函数会创建一个 "OpenCL program" 资源。
"Program" 对象实际上是一些精选的 OpenCL 内核(下文中再行讨论),但在实现 MetaQuotes 的过程中,OpenCL 程序中却明显只能有一个内核。要创建 "Program" 对象,应确保将源代码(此处为 - clSrc)读取到一个字符串中。
本例中无需如此,因为 clSrc 字符串已经被声明为一个全局变量:

下图所示为作为此前所创建上下文一部分的程序。

图 4. 程序为上下文的一部分
如果程序未能编译,则开发人员要在编译器的输出处独立发起一个数据请求。一个功能完善的 OpenCL API 拥有 API 函数 clGetProgramBuildInfo(),调用该函数后会在编译器输出处返回一个字符串。
当前版本 (b.642) 并不支持该函数,但很有必要将其加入 OpenCL API,从而为 OpenCL 开发人员提供有关内核代码正确性的更多详情。
来自设备(显卡)的 "Tongues"(语言)为命令队列,很明显,MQL5 不会在 API 层面上提供支持。
3.3. 创建内核
CLKernelCreate() 函数会创建一个 OpenCL 资源 "Kernel"(内核)。
int clKrn = CLKernelCreate( clPrg, "pi" );
所谓内核,就是一个在 OpenCL 设备上运行的程序中声明的函数。
在本例中,它就是名称为 "pi" 的 pi() 函数。"kernel" 对象就是内核的函数加上各自的自变量。该函数的第二个自变量为函数名称,应与程序中的函数名称完全匹配。

图 5. 内核
只要针对一个内核设置不同自变量,并将同一函数声明为内核,便可以尽量多次使用 "kernel" 对象。
现在,我们来说下 CLSetKernelArg() 和 CLSetKernelArgMem() 函数,不过先简单介绍下设备内存中存储的对象吧。
3.4. 内存对象
首先,我们要清楚,要在 GPU 上处理的任何“较大”对象,都要先在 GPU 本身的内存中创建,或是从主机内存 (RAM) 中移除。我们所说的“较大”对象是指缓冲区(一维数组)或是二维(2D)、三维(3D)的图像。
缓冲区是一个包含不同相邻缓冲区元素的大片存储区域。既可能是简单数据类型(字符、双精度、浮点、长型等),也可能是复杂数据类型(结构、并集等)。独立缓冲区元素可实现直接访问、读取和写入。
现在,我们要深入研究一下图像,因为它是一种独特的数据类型。该终端开发人员在 OpenCL 相关跟帖的首页上提供了代码,暗示开发人员并未参与到图像的使用中。
在引入的代码中,创建缓冲区的函数如下所示:
int clMem = CLBufferCreate( clCtx, _divisor * sizeof( double ), CL_MEM_READ_WRITE );
其中第一个参数是 OpenCL 缓冲区将其作为资源实现关联的一个上下文句柄;第二个参数是分配给该缓冲区的内存;而第三个参数则显示可以利用该对象完成哪些工作。返回值是 OpenCL 缓冲区(如已成功创建)的一个句柄或 -1 (如因某错误而无法创建)。
在本例中,缓冲区是在 GPU 内存(即 OpenCL 设备)中直接创建的。如果它未使用该函数即在 RAM 中创建,则要如下图所示被移往 OpenCL 设备内存 (GPU):
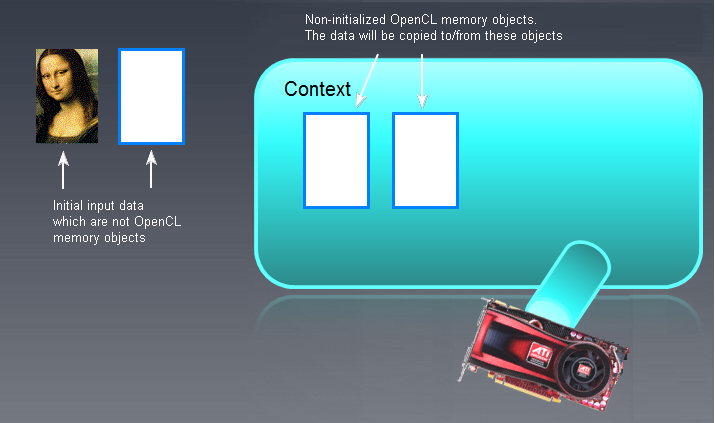
图 6. OpenCL 内存对象
左侧显示了 OpenCL 内存对象以外的输入/输出缓冲区(不一定是图像 - 此处的蒙娜丽莎仅作为说明用途!)。空的、未初始化的 OpenCL 内存对象在主要上下文字段中的显示位置要更靠右侧。初始数据“蒙娜丽莎”随后会被移至 OpenCL 上下文字段中,而且无论 OpenCL 程序输出何种内容,都需要移回左侧,即进入 RAM 中。
OpenCL 中在主机/OpenCL 设备间往来复制数据所用的术语如下:
写入命令(主机 -> 设备)会通过数据完成内存对象的初始化,同时在设备内存中放置该对象。
请牢记:设备中可用内存对象的有效性并未在 OpenCL 规格中指定,因为其取决于设备相应硬件的供应商。所以,创建内存对象时务必谨慎。
内存对象初始化完毕并写入设备后,图片就会如下所示:
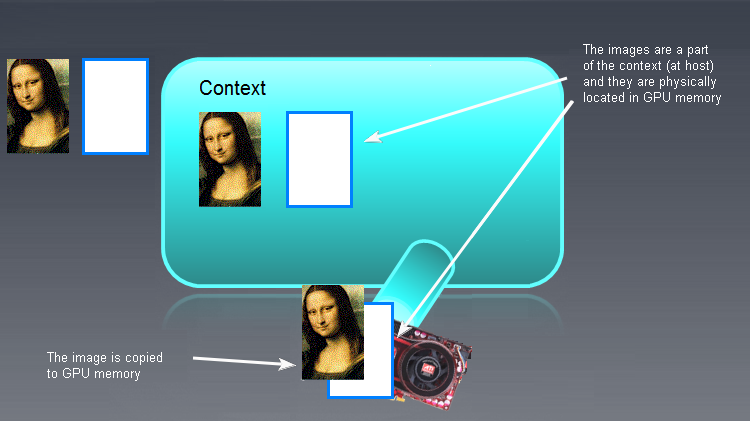
图 7. OpenCL 内存对象的初始化结果
现在,我们可以继续讲解用于设置内核参数的函数了。
3.5. 设置内核参数
CLSetKernelArgMem( clKrn, 0, clMem );
CLSetKernelArgMem() 函数会将此前创建的缓冲区定义为内核的一个零值参数。
如果现在来看一看内核代码中的相同参数,即能看到其显示如下:
__kernel void pi( __global float *out )
在内核中,与通过 API 函数 CLBufferCreate() 创建的类型相同的是 out[ ] 数组。
也有一个类似的函数用于设置非缓冲区参数:
bool CLSetKernelArg( int kernel, // handle to the kernel of the OpenCL program uint arg_index, // OpenCL function argument number void arg_value ); // function argument value
举个例子,如果我们决定将某个双精度 x0 设置为内核的第二个参数,则首先需要在 MQL5 程序中声明和初始化:
double x0 = -2;
而接下来还需调用该函数(也在 MQL5 代码中):
CLSetKernelArg( cl_krn, 1, x0 );
经过上述操作后,该图显示如下:
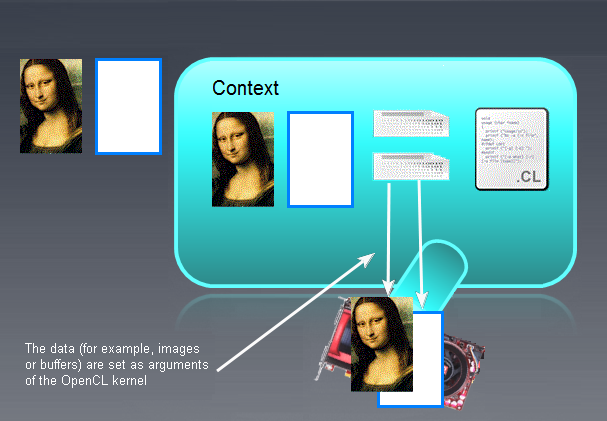
图 8. 内核参数的设置结果
3.6. 程序执行
bool ex = CLExecute( clKrn, 1, offs, works );
作者并未在 OpenCL 规格中发现对该函数的直接模拟。该函数会使用指定参数执行内核 clKrn。最后一个参数 'works' 会设置运算任务每次计算要执行的任务数量。该函数会证明 SPMD(单程序多数据)原理:每调用该函数一次,就会利用其自身的参数创建内核实例(其实例数量等于工作参数值);根据惯例,这些内核实例会同时执行,但是在不同的流核心上(对于 AMD 而言)。
OpenCL 的普遍性在于这种语言未绑定到代码执行过程中涉及的底层硬件基础架构:编码人员无需了解硬件规格即可正常执行 OpenCL 程序。该程序仍会被执行。不过仍强烈建议了解这些规格,以提升代码的效率(比如速度)。
比如说,此代码在作者未配备独立显卡的硬件设备上竟然运行良好。也就是说,作者对于发生仿真全过程的 CPU 本身的结构都很不了解。
到此为止,OpenCL 程序终于成功执行,现在我们可以在主程序中使用其结果了。
3.7. 读取输出数据
下面是主程序从设备读取数据的一部分:
float buf[ ]; ArrayResize( buf, _divisor ); uint read = CLBufferRead( clMem, buf );
请记住,从 OpenCL 中读取数据是指将该数据从设备复制到主机中。上述三行显示了其完成方式。只需在主程序中将同一类型的 buf[] 缓冲区声明为读取 OpenCL 缓冲区,再调用该函数即可。在主程序(本文是在 MQL5 语言中)中创建的缓冲区类型可与内核中的缓冲区类型不同,但其大小则必须完全匹配。
该数据现已复制到主机内存中,完全可供我们在主程序(即 MQL5 中的程序)中使用。
在 OpenCL 设备上完成所有必需的运算后,所有对象中的内存都应被释放。
3.8. 所有 OpenCL 对象的析构
该操作使用以下命令来完成:
CLBufferFree( clMem ); CLKernelFree( clKrn ); CLProgramFree( clPrg ); CLContextFree( clCtx );
这些函数系列的主要特点在于,对象应按其创建的相反顺序予以销毁。
现在,我们简单看一下内核代码本身。
3.9. 内核
可以看出,整个内核代码就是一个由多个字符串构成的单一长型字符串。
内核头部看起来与标准函数类似:
__kernel void pi( __global float *out )
针对内核头部有几项要求:
内核主体与 C 语言中的标准代码没有任何不同。
重要须知:字符串:
int i = get_global_id( 0 );
中的 i 为 GPU 内的用于确定该单元格内计算结果的若干计算单元。此结果会被进一步写入到输出数组(本例中是 out[])中,然后等到从 GPU 内存将数组读取到 CPU 内存中后,其值又会被添加到主程序中。
要注意的是,OpenCL 程序代码中的函数可能不只一个。例如,可以在“主”内核函数 pi() 中调用 pi() 函数以外的简单内联函数。稍后我们再进一步讨论这种情况。
现在,我们已经对 MetaQuotes 实现中的 OpenCL API 有了大致了解,可以继续尝试了。本文中,作者并不打算深入研究允许最大限度优化运行时间的硬件的详情。目前的主要任务,同样是提供 OpenCL 编程的入门知识。
换而言之,该代码还相当简单,因为它没有考虑硬件规格。同时,它又极具普遍性,所以可在任何硬件上执行 - AMD 出品的 CPU、IGP(CPU 中集成的 GPU)或 AMD / NVidia 出品的独立显卡。
在进一步研究采用向量数据类型进行简单优化之前,我们首先得熟悉它们。
向量数据类型专门针对 OpenCL,这将其与 C99 区分开来。其中包括任意的 (u)charN、(u)shortN、(u)intN、(u)longN、floatN 类型,其中 N = {2|3|4|8|16}。
这些类型应该用在我们清楚(或假设)内置编译器会设法实现其他并行计算的时候。这里我们需要注意,情况并不总是这样,即便是内核代码仅与 N 值有区别,而在其它各方面都完全一致(作者会自行判断)。
下表所示为 内置数据类型:

表 1. OpenCL 中的内置向量数据类型
任何设备都支持上述数据类型。每种数据类型都具有相应的 API 类型,用于实现内核与主程序之间的通信。这在目前的 MQL5 实施过程中并未提供,但问题不大。
其它类型也有,但应在使用时明确指定,因为并非所有设备都支持它们:

表 2. OpenCL 中的其它内置数据类型
此外,还有一些有待 OpenCL 提供支持的保留数据类型。它们在语言“规范”中占用了相当长的篇幅。
要声明一个向量类型的常量或变量,应遵循简单直观的原则。
下面列出了几个示例:
float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f); uint4 u = ( uint4 ) ( 1 ); /// u is converted to a vector (1, 1, 1, 1). float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) ); float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f ); float4 f = ( float4 ) ( 1.0f, 2.0f ); /// error
可以看出,只需将两相比对的、位于右侧的数据类型与左侧声明的变量“宽度”相匹配即可(此处为 4)。唯一例外就是在分量与标量相等的情况下发生的标量向向量的转换(第 2 行)。
所有向量数据类型都采用了一种简单的向量分量处理机制。它们一方面是向量(数组),另一方面又是结构。那么,比如说向量的第一分量宽度为 2 (例如 float2 u),则可作为 u.x 处理;而第二分量则作为 u.y 处理。
long3 u 类型向量的三个分量分别为:u.x、u.y、u.z。
至于 float4 u 类型向量,则依次会是 .xyzw,即 u.x、u.y、u.z、u.w。
float2 pos; pos.x = 1.0f; // valid pos.z = 1.0f; // invalid because pos.z does not exist float3 pos; pos.z = 1.0f; // valid pos.w = 1.0f; // invalid because pos.w does not exist
您可以一次选择多个分量,甚至对其重新排列(组标记):
float4 c; c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); c.z = 1.0f; c.xy = ( float2 ) ( 3.0f, 4.0f ); c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f ); float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 swiz= pos.wzyx; // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f ) float4 dup = pos.xxyy; // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )组标记分量,即多个分量的规格,可能会出现在赋值语句的左侧(即左值):
float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f ); pos.xw = ( float2 ) ( 5.0f, 6.0f ); // pos = ( 5.0f, 2.0f, 3.0f, 6.0f ) pos.wx = ( float2 ) ( 7.0f, 8.0f ); // pos = ( 8.0f, 2.0f, 3.0f, 7.0f ) pos.xyz = ( float3 ) ( 3.0f, 5.0f, 9.0f ); // pos = ( 3.0f, 5.0f, 9.0f, 4.0f ) pos.xx = ( float2 ) ( 3.0f, 4.0f ); // invalid as 'x' is used twice pos.xy = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // mismatch between float2 and float4 float4 a, b, c, d; float16 x; x = ( float16 ) ( a, b, c, d ); x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw ); x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz ); // invalid as the component a.xxxxxxx is not a valid vector type
各个分量都可利用另一标记进行访问,这些标记包括十六进制数字前插入的字符 s (或 S),或是组标记中的多个数字:
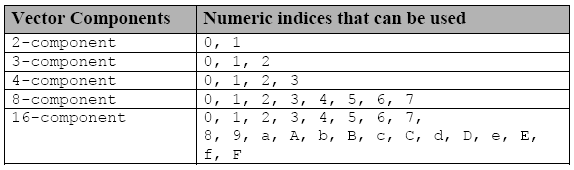
表 3. 用于访问向量数量类型各个分量的索引
如果您声明一个向量变量 f
float8 f;则 f.s0 是向量的第 1 个分量,f.s7 是第 8 个分量。
float16 x;则 x.sa (或 x.sA)是向量 x 的第 11 个分量;而 x.sf (或 x.sF)则指向量 x 的第 16 个分量。
数值索引 (.s0123456789abcdef) 与字母标记 (.xyzw) 不得与带有分量组标记的相同标识符混淆。
float4 f, a; a = f.x12w; // invalid as numeric indices are intermixed with the letter notations .xyzw a.xyzw = f.s0123; // valid
最后,还有一种方法来操作采用 .lo、.hi、.even、.odd 的向量类型分量。
其后缀使用如下:
例如:
float4 vf; float2 low = vf.lo; // vf.xy float2 high = vf.hi; // vf.zw float2 even = vf.even; // vf.xz float2 odd = vf.odd; // vf.yw
此标记可以重复使用,直到出现一个标量(非向量数据类型)为止。
float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f ); float2 s = u.lo.lo; // ( 1.0f, 2.0f ) float2 t = u.hi.lo; // ( 5.0f, 6.0f ) float2 q = u.even.lo; // ( 1.0f, 3.0f ) float r = u.odd.lo.hi; // 4.0f
至于 3 分量向量类型,其情况就稍微复杂一些:严格来讲,它是一个 4 分量向量类型,且第 4 分量的值未定义。
float3 vf = (float3) (1.0f, 2.0f, 3.0f); float2 low = vf.lo; // ( 1.0f, 2.0f ); float2 high = vf.hi; // ( 3.0f, undefined );
简单的运算规则 (+, -, *, /)。
针对同一维度的向量定义所有指定的算术运算,并按分量逐个完成。
float4 d = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f ); float4 w = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f ); float4 _sum = d + w; // ( 6.0f, 10.0f, 13.0f, 3.0f ) float4 _mul = d * w; // ( 5.0f, 16.0f, 30.0f, -4.0f ) float4 _div = w / d; // ( 5.0f, 4.0f, 3.333333f, -0.25f )
唯一例外是一个操作数为标量,而另一个为向量的情况。在这种情况下,标量类型会被计算为向量中声明的数据类型,同时,标量本身也会被转换为一个维度与向量操作数相同的向量。接下来再执行一次算术运算。关系运算符 (<, >, <=, >=) 也是如此。
OpenCL 语言还支持可能由内置数据类型构成的派生的 C99 原生数据类型(比如结构、并集、数组等),这些内置数据类型列在了本章节首个图表中。
还有最后一件事:如果您要使用 GPU 进行精确计算,那么毫无疑问,必须使用双精度数据类型以及随之而来的 doubleN。
为此,只需将以下行:
#pragma OPENCL EXTENSION cl_khr_fp64 : enable
插入到内核代码的开头处即可。
此信息已足够您理解以下大部分内容。如果您有任何疑问,请参阅《OpenCL 1.1 规范》。
说实在的,作者未能立即编写出一个带有向量数据类型的工作代码。
开始时,作者并未过多注意阅读语言规范,而是觉得只要在内核中声明一个向量数据类型(例如 double8),一切问题都会自然解决了。而且,作者所尝试的仅将一个输出数组声明为 double8 向量的数组这一做法也失败了。
我过了一段时间才意识到,要有效完成内核的向量化并实现真正的加速,这些还绝对不够。通过将结果输出到向量数组中还无法解决这一问题,因为不仅需要能快速输入和输出数据,还需要对其进行快速计算。如果顺利实现,则可加速进程并提升效率,使得最终有可能开发出一套更快的代码。
但事情没这么简单。尽管上述内核代码几乎可以实现盲调,但由于使用了向量数据,查找错误已变得相当困难。我们可以从此类标准消息
ERR_OPENCL_INVALID_HANDLE - invalid handle to the OpenCL program
或以下消息中
ERR_OPENCL_KERNEL_CREATE - internal error while creating an OpenCL object
得到哪些富有建设性的信息呢?
因此,作者不得不求助于 SDK。在这种情况下,考虑到作者的硬件配置,碰巧是 Intel OpenCL SDK 提供的 Intel OpenCL SDK 离线编译器(32 位)(适用于 Intel 之外的 CPU/GPU,SDK 也应包含相关的离线编译器)。因为它允许在不绑定到主机 API 的情况下调试内核代码,所以非常方便。
您只需将内核代码插入到编译器窗口(尽管未使用 MQL5 代码中采用的形式,而是替换成了没有外部引用字符和 "\r\n" (回车字符)),并按下带有齿轮图标的 Build 按钮即可。
如此一来,Build Log (构建日志)窗口就会显示与构建过程及其进展相关的信息:
图 9. Intel OpenCL SDK 离线编译器中的程序编译
为了获取不含引用字符的内核代码,用主机语言 (MQL5) 编写一个简单程序 WriteCLProgram() 会很有用,该程序可将内核代码输出到文件。现已将其包含在主程序代码中。
编译器的消息并不总是很明确,但已经比当前 MQL5 可提供的多很多了。可以在编译器中即时修复错误,而且一旦您确定没有任何错误,就可以使用 MetaEditor 将修复程序传送到内核代码中。
还有最后一件事。作者最初的想法是开发出一种向量化代码,该代码能够通过设置单一全局变量 "number of the channels"来处理 double4、double8 和 double16。好几天来作者一直在费劲地使用拼接操作符 ## (出于某种原因该符号无法在内核代码中进行操作),最终还是完成了。
在此期间,作者成功地开发出一个含有三个内核代码(其中每个都适合其大小 - 4、8 或 16)的脚本的工作代码。虽然本文不会提供此中间代码,但还是值得一提,因为您可能想轻松编写一个内核代码。此脚本实施的代码 (OCL_pi_double_several_simple_kernels.mq5) 附于本文末尾的下方。
这里是向量化内核的代码:
"/// enable extensions with doubles \r\n" "#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _intrnCnt ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" "#define _CH " + i2s( _ch ) + " \r\n" "#define _DOUBLETYPE double" + i2s( _ch ) + " \r\n" " \r\n" "/// extensions for 4-, 8- and 16- scalar products \r\n" "#define dot4( a, b ) dot( a, b ) \r\n" " \r\n" "inline double dot8( double8 a, double8 b ) \r\n" "{ \r\n" " return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi ); \r\n" "} \r\n" " \r\n" "inline double dot16( double16 a, double16 b ) \r\n" "{ \r\n" " double16 c = a * b; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot4( c.lo.lo + c.lo.hi + c.hi.lo + c.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double16 v16 = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 ); \r\n" " double8 v8 = v16.lo; \r\n" " double4 v4 = v16.lo.lo; \r\n" " double2 v2 = v16.lo.lo.lo; \r\n" " \r\n" " /// all vector-related with the calculated type \r\n" " _DOUBLETYPE in; \r\n" " _DOUBLETYPE xVect; \r\n" " _DOUBLETYPE sumVect = ( _DOUBLETYPE ) ( 0.0 ); \r\n" " _DOUBLETYPE doubleOneVect = ( _DOUBLETYPE ) ( 1.0 ); \r\n" " _DOUBLETYPE doubleCHVect = ( _DOUBLETYPE ) ( _CH + 0. ); \r\n" " _DOUBLETYPE doubleSTEPVect = ( _DOUBLETYPE ) ( _STEP ); \r\n" " \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in = v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j ); \r\n" " xVect = ( in + 0.5 ) * doubleSTEPVect; \r\n" " sumVect += 4.0 / ( xVect * xVect + 1. ); \r\n" " } \r\n" " out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n" "} \r\n";
除了设置“向量通道”数量的新全局常量 _ch 以及变小了好几倍的 _ch 的全局常量 _intrnCnt 以外,外部主程序的变化不大。正因为此,作者决定不在此展示主程序了。可以在本文末尾下方随附的脚本中找到该程序 (OCL_pi_double_parallel_straight.mq5)。
可以看出,除了内核 pi() 的“主”函数之外,现在我们已有两个用于确定向量 dotN( a, b ) 的无向积的内联函数,以及一个宏置换。由于 OpenCL 中的 dot() 函数被定义为与维数不超过 4 的向量相关,所以包括了这些函数。
之所以使用可重新定义 dot() 函数的 dot4() 宏,只是为了方便调用带有所计算名称的 dotN() 函数:
" out[ i ] = dot" + i2s( _ch ) + "( sumVect, doubleOneVect ); \r\n"
如果我们使用的是通常不带指数 4 形式的 dot() 函数,则当 _ch = 4 (向量化通道数量为 4)时,我们将无法如此轻松地调用它。
这一行说明了特定内核形式(其特点在于此类内核在主程序中作为一个字符串进行处理)的另一个有用功能:我们可以在内核中使用计算得出的标识符,不仅包括函数标识符,还包括数据类型标识符!
下面随附了含有该内核的完整主程序代码 (OCL_pi_double_parallel_straight.mq5)。
运行带有 "width" 为 16 ( _ch = 16 ) 向量的脚本后,可得到以下结果:
2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) ================================================== 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) CPUtime / GPUtime = 4.130 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The time to calculate PI was 8.830 seconds 2012.05.15 00:15:47 OCL_pi_double2_parallel_straight (EURUSD,H1) SMARTER: The value of PI is 3.141592653590 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The time to calculate PI was 8.002 seconds 2012.05.15 00:15:38 OCL_pi_double2_parallel_straight (EURUSD,H1) DULL: The value of PI is 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: gone = 2.138 sec. 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) OPENCL: pi = 3.141592653590 2012.05.15 00:15:30 OCL_pi_double2_parallel_straight (EURUSD,H1) read = 20000 elements 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) CLProgramCreate: unknown error. 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.15 00:15:28 OCL_pi_double2_parallel_straight (EURUSD,H1) ==================================================
可以看出,即使是使用向量数据类型进行优化,也无法让内核变快。
但是,如果在 GPU 上运行相同代码,则速度增加要明显得多。
根据 MetaDriver 提供的信息(显卡为 HIS Radeon HD 6930,CPU 为 AMD Phenom II x6 1100T),同样的代码会产生以下结果:
2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) ================================================== 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) CPUtime / GPUtime = 84.983 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The time to calculate PI was 14.617 seconds 2012.05.14 11:36:07 OCL_pi_double2_parallel_straight (AUDNZD,M5) SMARTER: The value of PI is 3.141592653590 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The time to calculate PI was 14.040 seconds 2012.05.14 11:35:52 OCL_pi_double2_parallel_straight (AUDNZD,M5) DULL: The value of PI is 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: gone = 0.172 sec. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) read = 20000 elements 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) CLProgramCreate: unknown error. 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125 2012.05.14 11:35:38 OCL_pi_double2_parallel_straight (AUDNZD,M5) ==================================================
这里还有一个内核(可以在以下随附的 OCL_pi_double_several_simple_kernels.mq5 文件中找到,但这里就不演示了)。
该脚本实现了作者此前的想法,当时他临时放弃了编写“单一”内核模块的尝试,并打算针对不同的向量维数 (4, 8, 16, 32) 编写四个简单的内核模块:
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable \r\n" "#define _ITERATIONS " + i2s( _itInKern ) + " \r\n" "#define _STEP " + d2s( _step, 12 ) + " \r\n" " \r\n" "typedef struct \r\n" "{ \r\n" " double16 lo; \r\n" " double16 hi; \r\n" "} double32; \r\n" " \r\n" "inline double32 convert2double32( double a ) \r\n" "{ \r\n" " double32 b; \r\n" " b.lo = ( double16 )( a ); \r\n" " b.hi = ( double16 )( a ); \r\n" " return b; \r\n" "} \r\n" " \r\n" "inline double dot32( double32 a, double32 b ) \r\n" "{ \r\n" " double32 c; \r\n" " c.lo = a.lo * b.lo; \r\n" " c.hi = a.hi * b.hi; \r\n" " double4 _1 = ( double4 ) ( 1., 1., 1., 1. ); \r\n" " return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo + c.lo.hi.hi + \r\n" " c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo + c.hi.hi.hi, _1 ); \r\n" "} \r\n" " \r\n" "__kernel void pi( __global double *out ) \r\n" "{ \r\n" " int i = get_global_id( 0 ); \r\n" " \r\n" " /// define vector constants \r\n" " double32 _v32; \r\n" " _v32.lo = ( double16 ) ( 0., 1., 2., 3., 4., 5., 6., 7., \r\n" " 8., 9., 10., 11., 12., 13., 14., 15. ); \r\n" " _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23., \r\n" " 24., 25., 26., 27., 28., 29., 30., 31. ); \r\n" " \r\n" " /// all vector-related with undefined type \r\n" " double32 xVect; \r\n" " double32 sumVect = convert2double32( 0.0 ); \r\n" " double32 double1Vect = convert2double32( 1.0 ); \r\n" " \r\n" " double32 in; \r\n" " /// work only with 16-vectors in the loop! \r\n" " for( long j = 0; j < _ITERATIONS; j ++ ) \r\n" " { \r\n" " in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j ); \r\n" " in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j ); \r\n" " xVect.lo = ( in.lo + 0.5 ) * _STEP; \r\n" " xVect.hi = ( in.hi + 0.5 ) * _STEP; \r\n" " sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. ); \r\n" " sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. ); \r\n" " } \r\n" " out[ i ] = dot32( sumVect, double1Vect ); \r\n" "} \r\n";
该内核模块实施的是向量维数 32。新向量类型和几个必要的内联函数均在该内核的主函数以外进行了定义。除此之外(这很重要!),主循环内的所有计算都只有意地使用标准向量数据类型制成;非标准类型会在循环外进行处理。这样便能够大幅缩短代码的执行时间。
在我们的计算中,该内核看起来并不比用于宽度为 16 的向量慢,但也快不了多少。
根据 MetaDriver 提供的信息,含该内核 (_ch=32) 的脚本会产生下述结果:
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec. 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590 2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: unknown error or no error. 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; vectorization channels - 32 2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================
作者心里非常清楚,用作说明 OpenCL 资源的任务对于此语言来说并不是特别典型。
如果只是翻开一本教科书、照搬一个大型矩阵乘的标准示例放到这里,则会简单得多。很明显,那样的示例一定让人印象深刻。但是,是否有大量 mql5.com 论坛用户参与到需要大型矩阵相乘的金融运算呢?这很值得怀疑。作者想要选择自己的示例,克服其本人曾遭遇的所有困难,同时尝试与他人分享经验。当然,你们才是评判者,亲爱的论坛用户们。
与使用 MetaDriver 脚本后获得的大量效率提升相比,OpenCL 仿真(仅通过 CPU 进行)所实现的效率提升已被证明是微不足道。但在某个适合的 GPU 上,即使我们忽略在 AMD 的 CPU 上运行时间稍长这一事实,它至少也会比通过仿真实现的效率提升高出一个数量级。OpenCL 仍值得学习,尽管其在运算速度方面的提升极其有限!
作者的下一篇文章有望解决真实硬件上 OpenCL 抽象模式显示特性的相关问题。具备这些方面的知识,有时可以在相当程度上进一步加快运算速度。
作者要在这里特别感谢 MetaDriver 提供极为宝贵的编程与性能优化建议,同时感谢支持团队提供了使用 Intel OpenCL SDK 的可能性。
随附文件目录如下:

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...