第一篇文章《OpenCL:连接并行世界的桥梁》是对 OpenCL 主题内容的一个简要介绍。它解决了 OpenCL 中程序(尽管不太准确,但亦称为一个内核)与 MQL5 的外部(主机)程序之间交互的基本问题。有些语言的性能(比如向量数据类型的使用),都是通过 pi = 3.14159265... 的计算举例证明。
某些情况下程序的性能有可观的优化空间。但是,前文所述的都是朴素优化,因为它们并未考虑到执行所有计算要用到的硬件规格。而大多数情况下,此类规格的相关知识会让我们明明白白地实现明显超越 CPU 性能的提速。
为论述此类优化,作者不得不求助于那个不再原始、很可能是 OpenCL 相关文献中研究最为完善的一个示例。即两个大型矩阵相乘。
我们进入主题 - OpenCL 存储模型以及其在实际硬件架构上实施的独特性。
1.1. OpenCL 存储模型
一般来说,根据计算机平台,各存储系统彼此之间的差异很大。比如说,现代所有的 CPU 都支持自动数据缓存;而与之对照的 GPU 却并不总是这样。
为确保代码的可移植性,OpenCL 中采用了一种抽象存储模型,需要在实际硬件上实施此模型的程序员和提供商都可以遵照。理论上,OpenCL 中定义的存储如下图所示:
图 1. OpenCL 存储模型
一旦将数据从主机传输到设备,就会将其存储于全局设备内存中。按相反方向传输的任何数据,亦会存储于全局内存中(但这次是到全局主机内存中)。关键词 __global (双下划线!)是一个修饰符,表示与特定指针关联的数据已被存储于全局内存中:
__kernel void foo( __global float *A ) { /// kernel code }
设备中的所有计算单元均可访问全局内存,就像主机系统中的 RAM 一样。
而常量存储器,与其名称不同的是,并不一定存储只读数据。该存储类型专为那些每个元素都可以同时被所有 工作单元访问的数据而设计。带有常数值的变量当然亦归入此类。OpenCL 模型中的常量存储器,是全局内存的一部分,而传输到全局内存的存储对象,则可因此指定为 __constant。
本地内存是指每个设备专用的高速暂存存储器。硬件中,它通常以片上存储器的形式存在,但是对于 OpenCL 没有完全相同的特定要求。
访问此类存储会导致低得多的延迟,而存储带宽亦会因此比全局存储大得多。我们会试着充分利用其较低的延迟来优化内核性能。
根据 OpenCL 规范,本地内存中的变量既可以在内核头中声明:
__kernel void foo( __local float *sharedData ) { }亦可在其主体内声明:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }注意:动态数组不能在内核主体中声明;您始终都要指定其大小。
在下面针对两个大型矩阵相乘的内核优化过程中,您可以看出如何处理本地数据,以及作者经历过的、其于 MetaTrader 5 中蕴含的实施特征。
不包含指针的局部变量与内核自变量默认都是私有型(如指定为不带 __local 修饰符)。实际情况中,这些变量通常都位于寄存器中。反过来也是一样,私有数组与 任何溢出寄存器通常都位于片外存储,即较高的延迟存储。我们引用一些维基百科的相关信息:
在许多编程语言中,编程人员都会有任意地配置许多变量的错误观念。但在编译时,编译器必须决定在一个较小及有限寄存器组的系统中如何分配这些变量。并非所有变量都是在同一时间使用(或“活动”),所以有些寄存器可能被分配超过一个变量。然而,两个变量若在同一时间使用,就不可能在不破坏其值的情况下分配给相同的寄存器。
无法被分配到相同寄存器的变量必须保留在 RAM(随机存取存储器)中,在需要读取或写入时才会被加载,这个过程被称为溢出。RAM 访问速度明显低于寄存器访问速度,这会降低编译程序的运行速度,所以一个经过优化的编译器会尽可能的将更多的变量放置在寄存器。寄存器压力这个词被使用在当硬件寄存器数量比起理想数量少的状况,高压的情况通常代表需要更多溢出及重载。
我们所说的 OpenCL 内存模型与现代 GPU 的存储结构非常相似。下图显示了 OpenCL 内存模型与 GPU AMD Radeon HD 6970 内存模型之间的关联。
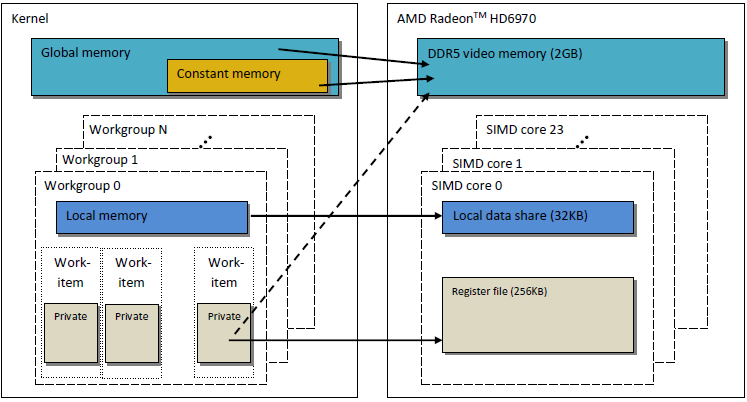
图 2. Radeon HD 6970 存储结构与抽象 OpenCL 内存模型的关联
我们继续更加详细地研究研究与具体 GPU 内存实施相关的问题。
1.2. 现代独立 GPU 中的内存
1.2.1. 合并内存请求
对于内核性能的优化,此信息亦非常重要,因为主要目标是达到高存储带宽。
看一看下图,更好地了解一下内存寻址过程:
图 3. 全局设备内存中的寻址数据图
假设指向某个整型变量 int 数组的指针为地址 Х = 0x00001232。每个 int 占用 4 字节内存。假设某线程(是对执行内核代码的某工作单元的一种软件模拟)的地址数据位于 Х[ 0 ]:
int tmp = X[ 0 ];
我们假设存储总线宽度为 32 字节(256 位)。这种总线宽度在 Radeon HD 5870 之类的强大 GPU 中很常见。而其它某些 GPU 的数据总线宽度可能有所不同,比如有些 NVidia 型号达到 384 位甚至 512 位。
存储总线的寻址要与其结构对应,即首要的是其宽度。换言之,内存中的数据存储于每一个 32 字节(256 位)的块中。不管我们在 0x00001220 到 0x0000123F 的范围内如何编址(此范围内都是精确的 32 字节,您可以自己看),我们都会得到地址 0x00001220 作为读取的起始地址。
访问地址 0x00001232 会返回地址在 0x00001220 到 0x0000123F 范围内的所有数据,即 8 个 int 数字。因此,仅有 4 个字节(一个 int 数字)的有用数据,而其余的 28 个字节(7 个 int 数字)则无用:
图 4. 由内存获取所需数据的方案图
我们需要的位于之前指定地址 - 0x00001232 - 处的数字,已包含于方案图之中。
为能最大化使用此总线,GPU 尝试把通过不同线程访问的内存合并成为一个单一的存储请求;存储访问越少越好。背后的原因在于,访问全局设备内存会占用我们的时间,并由此极大地影响程序运行速度。看一看内核代码的下一行:
int tmp = X[ get_global_id( 0 ) ];
假设我们的数组 Х 来自前文给出的示例。那么,前 16 个线程(内核)就会访问从 0x00001232 到 0x00001272 的地址(此范围内有 16 个 int 数字,即 64 字节)。如果每个请求都通过内核独立发送,无需提前合并到一个单一内核中,那么 16 个请求中的每一个都会包含 4 字节的有用数据以及 28 字节的无用数据,所以总共就是 64 个已用字节以及 448 个未用字节。
此计算基于每次访问位于同一 32 字节存储块中某个地址都会返回绝对一致数据的事实。这是关键所在。将多个请求合并到单一、一致的请求会更加准确,从而减少无用的请求。此操作于下文均称为合并,而按此合并的请求则被称为相干性。
图 5. 获取所需数据仅需三个存储请求
上图中每个单元格均为 4 字节。本例中, 3 个请求便已足够。如果数组的开头已按地址与每个 32 字节的存储块的开头地址对齐,那么甚至 2 个请求就够了。
在 AMD GPU 64 中,线程是波前的一部分,并因此应按 SIMD 执行中的相同指令执行。按 get_global_id( 0 ) 排列的 16 个线程,刚好是波前的四分之一,都被合并为一个相干请求,有实现总线的高效使用。
下图所示,是一致性请求所需存储带宽与非相干性(即“自发”请求)的对比说明。这里使用的是 Radeon HD 5870,但 NVidia 显卡亦可见类似结果。
图 6. 相干与非相干请求所需存储带宽的对比分析
可以清楚地看出,相干存储请求允许将存储带宽加大一个数量级。
1.2.2. 存储库
存储器由数据实际存放的库构成。在现代 GPU 中,通常都是 32 位(4 字节)字。串行数据存放于相邻的存储库中。访问串行元素的线程组不会出现任何库冲突。
而库冲突的最大负面影响,则见于本地 GPU 内存当中。因此,最好是通过定位于不同存储库的相邻线程来访问本地数据。
在 AMD 硬件上,产生库冲突的波前直到所有本地内存操作结束之后才会停止。如此会导致串行化,要并行执行的代码块会借此串行执行。它对内核的性能有极其负面的影响。
图 7. 不存在库冲突的存储访问方案图
上图所示为不带库冲突的存储访问,因为所有线程都访问不同的数据。
我们再来看一看存在库冲突的存储访问:
图 8. 存在库冲突的存储访问
但这一情况有例外:如果所有访问都是到一个相同的地址,则库可以执行一次广播以避免延迟:
图 9. 所有线程均访问同一个地址
访问全局内存时也会出现类似事件,但这种冲突的影响微乎其微。
以下方列出的 Radeon 5xxx 系列中的部分显卡规格为例:
图 10. 中高端 Radeon HD 58xx 显卡的技术规格
现在,我们继续编程。
2.1. MQL5 代码
对比前一篇文章《OpenCL:连接并行世界的桥梁》,手头的是标准任务,即两个矩阵相乘。之所以选择它,是因为从各个不同的来源渠道,都能找到大量有关此主题的信息。它们大都是通过这样或那样的方式,提供或多或少的协调解决方案。这就是我们要走的路,一步一步地澄清模型结构的意义,同时牢记:我们面对的是实际硬件。
下面是一个在线性代数领域中著名的矩阵乘法公式,专门针对计算机运算进行了修改。第一个指数是矩阵行号,第二个是列号。通过顺序将第一与第二矩阵中的每一个元素连续积添加到累积和的方式,计算出每一个输出矩阵元素。最终,此累积和就是计算得出的输出矩阵元素:
图 11. 矩阵乘法公式
图示如下:
图 12. 矩阵乘法算法(以某输出矩阵元素的计算为例)图解
很容易就可以看出,只要两个矩阵的维数都等于 N,则相加与相乘的次数都可以通过函数 O(N^3) 估算得出:要计算每一个输出矩阵元素,您需要获取第一矩阵中某行与第二矩阵中某列的无向积。它大约需要 2*N 次相加和相乘。所需的估算通过乘以矩阵元素数量 N^2 获取。由此,粗略的代码运行时在相当大程度上取决于 N 的次方。
下文出于方便目的,矩阵的行数与列数均设置为 2000;它们可以为任意数字,但不能太大。
MQL5 中的代码并非十分复杂:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
列表 1. 主机上的初始顺序程序
采用不同参数的性能结果:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
可以看出,我们对于运行时对线性矩阵尺寸依赖性的估算看起来是正确的:所有矩阵维数增加两倍,就会导致运行时增加大约 8 倍。
简单说说这种算法:循环顺序可以在乘法函数 mul() 中任意更改。结果表明它对运行时有相当大的影响:最慢与最快运行时变量的比率约为 1.73。
本文仅阐述了最快变量;其余经过测试的变量,均见本文末尾处随附的代码(matr_mul_2dim.mq5 文件)。在这方面,《OpenCL 编程指南》 (Aaftab Munshi、Benedict R. Gaster、Timothy G. Mattson、James Fung、Dan Ginsburg) 中曾作如下陈述(第 512 页):
显然这些并非我们可以实施的初始“非并行”代码的全部优化。有一些与硬件((S)SSEx 指令)相关,而其它的则是纯粹的算法,比如 施特拉森算法, 铜匠维诺格拉特算法等。注意:导致速度大幅度超越传统算法的施特拉森算法的相乘矩阵尺寸非常小,仅为 64х64。本文中,我们会学习线性尺寸高达几千(大约高达 5000)的快速相乘矩阵。
2.2. 该算法于 OpenCL 中的第一次实施
现在,我们将此算法移植到 OpenCL,创建 ROWS1 (行1)* COLS2 (列2)线程,即由内核中删除两个外层循环。每个线程都会执行 COLSROWS 迭代,让内部循环仍是内核的一部分。
由于我们必须要为 OpenCL 内核创建三个线性缓冲区,所以有必要重新调整初始算法,以使其与此内核算法尽量接近。带有线性缓冲区的“单核 CPU”上,会随同内核代码一起,提供“非并行”程序代码。带有二维数组的代码的最优性,并不意味着其仿真亦针对线性缓冲区最优:必须重复所有测试。因此,我们再一次选择 c-r-cr 作为与线性代数中矩阵乘法标准逻辑对应的初始变量。
也就是说,要避免矩阵/缓冲区寻址混淆,请回答主要问题:如果矩阵 Matr (M 行乘以 N 列)在 GPU 内存中排列为一个线性缓冲区,那么我们该如何计算某元素 Matr[ row ][ column ] 的线性偏移呢?
事实上,GPU 内存中的矩阵布局并没有什么固定顺序,因为它是由问题的逻辑单独决定的。例如:两个矩阵的元素在缓冲区排列方面可以有所不同,因为就所涉的矩阵相乘算法而言,矩阵是非对称的,即第一矩阵的行乘以第二矩阵的列。如此重新安排,可以极大地影响到每次内核迭代中,从全局 GPU 内存顺序读取矩阵元素的运算性能。
该算法的第一次实施,会带有同样方式排列的矩阵 - 按行优先顺序。首先将第一行元素放入缓冲区,然后是第二行的所有元素,如此递推。下述为扁平公式,线性存储上方矩阵 Matr[ M (rows) ][ N (columns) ] 的一种二维体现:
图 13. 将二维索引空间转化为在 GPU 缓冲区内线性排列矩阵的算法
上图还举例说明了在线性存储上按列优先顺序呈二维矩阵表示的方式。
下面是一个我们在 OpenCL 设备上执行的程序首次实施的代码,经过少量删减:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
列表 2. OpenCL 中程序的首次实施
最后两个函数会在验证计算的准确性时用到。文末附有完整代码 (matr_mul_1dim.mq5)。注意:维数不必只与方块矩阵对应。
更深一步的变更几乎始终只关系到内核代码,因此下文只谈内核修改代码。
引入 REALTYPE 类型,是为了方便将计算精确度从浮点型改为双精度。应当指出的是,REALTYPE 类型不仅在主机程序中声明,还在内核中声明。如有必要,有关此类型的任何变更,都要在两个地方同时做出——主机程序的 #define 与内核代码的 #define 。
代码执行结果(下文皆为浮点数据类型)
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
如在 Radeon HD 4870 (_device = 1) 上执行:
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
可以看出,此内核在 GPU 上的执行要慢得多。但是,我们还未专门针对 GPU 进行优化。
几条结论:
我们知道,一个维数为 2000 的矩阵,其每个元素的计算大约需要 2 * 2000 次加法/乘法。通过乘以矩阵元素的数量 (2000 * 2000),就会得出 160 亿次浮点型数据运算的总数。也就是说,CPU 上的此次执行用时 115.628 秒,对应着下述数据流速度
另一方面,要知道迄今为止矩阵维数为 2000 的“单核 CPU”的最快运算,其完成仅 83.663 秒(请参见我们第一个不带 OpenCL 的代码)。因此
我们以此数据作为参照,作为我们优化的起始点。
与之类似,CPU 上利用 OpenCL 进行的计算会得到:
最后,计算 GPU 上的吞吐量:
2.3. 消除非相干数据访问
从该内核代码中,您很容易就会看到几个非最优项。
查看一下内核中循环的主体:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
很容易看出,运行循环计数器 (cr++) 时,会从第一个缓冲区 in1[] 中取连续数据。而来自第二缓冲区 in2[] 的数据,则以 COLS2 为“间隔”获取。换句话说,从第二缓冲区获取的数据的主要部分都没用,因为存储请求将是非相干的(参见 1.2.1. 合并内存请求)。要处理好这种情况,通过更改数组 in2[] 中索引的计算公式及其生成模式,修改三处代码即足够:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];现在,当循环计数器 (cr++) 值变化时,两个数组的数据都会被顺序获取,不带任何“间隔”。
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- checkRandom() 函数中的验证码:
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];CPU 上的性能结果:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
可以看出,数据的相干访问几乎对 GPU 上的运行时没有任何影响;但却明显地改进了 CPU 上的运行时。它极有可能关系到稍后优化的因素,尤其是我们要尽快摆脱掉的、访问全局变量的超高延迟。
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
该新内核代码,请见文末的 matr_mul_1dim_coalesced.mq5。
内核代码列出如下:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
列表 3. 带有已合并全局存储数据访问的内核
现在,我们继续进一步优化。
众所周知,全局 GPU 存储访问的延迟极其之高(约 600-800 个周期)。比如说,执行一次两个数的加法,就有大约 20 个周期的延迟。在 GPU 上计算时,优化的主要目标就是通过增加计算的吞吐量来隐藏延迟。在此前开发的内核循环中,我们不断地访问全局存储元素,所以浪费了大量的时间。
现在,我们将局部变量和引入内核(可以实现速度提高多倍的访问,因为它是工作单元寄存器中内核的一个私有变量),并待循环结束后,逐一将获取的和值分配给输出数据的元素:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
列表 4. 引入私有变量以计算无向积计算循环中的累积和
完整源代码文件请见文末随附的 matr_mul_sum_local.mq5。
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================这是一次真正的生产率提升!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
顺序优化过程中,我们努力坚持的主要原则如下:首先,您要按照可能的最完善的方式来重新安排数据结构,以使其适于给定的任务、尤其是基础硬件。然后再采用 mad() 或 fma() 之类的快速计算算法,继续精细优化。您要牢记:顺序优化并不一定会导致性能提升 - 这一点不能保证。
2.5. 改进内核执行的操作
在并行编程中,重要的是按照并行运行结构最小化间接成本(所用时间)的组织计算。在维数为 2000 的矩阵中,一个计算某输出矩阵元素的工作单元,会执行占整体任务 1 / 4000000 的工作量。
这很明显太多了,而且与硬件上执行计算的实际单元数量相差甚远。现在,在内核的这个新版本中,我们会计算整个矩阵行,而不是一个元素。
重要的是,现在的任务空间已经从二维变成了一维作为整体的维度 - 整行(而不是矩阵的单一元素)现已于内核的每个任务中进行计算。因此,任务空间转化成为矩阵的行数。
图 14. 输出矩阵整行计算的方案图
内核代码变得更加复杂:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 5. 用于输出矩阵整行计算的内核
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
性能结果(完整的源代码请见 matr_mul_row_calc.mq5):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
我们可以看出,CPU 上的运行时明显恶化,而且在 GPU 上也略微变差(虽然不明显)。也不是全都这么糟糕:这种局部情况暂时恶化的策略变更,只是为了进一步大幅提升其性能。
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. 将第一数组的行迁移到私有内存
矩阵相乘算法的主要特征,就是带有伴随结果累积的大量乘法。此算法的一种恰当、高质量的优化,则应意味着数据传输的最小化。但到目前为止,在无向积累积的主循环计算过程中,我们所有的内核修改都存储于全局内存的三个矩阵中的其中两个。
这就意味着,每个无向积(实际上是每个输出矩阵元素)的所有输入数据,都通过整个存储层次(从全局到私有)以相关延迟持续优化。针对输出矩阵每一经过计算的行,通过确保每个工作单元都重复使用第一矩阵的同一行来减少流量。
图 15. 将第一矩阵的行迁移到工作单元的私有内存
无需在主机程序代码中做任何修改。而且,内核中的改动也极其细微。鉴于中间一维私有数组在内核中生成的事实,GPU 试着将其置于执行此内核的单元的私有内存中。把第一矩阵所需行从全局复制到私有内存中。也就是说,值得注意的是,即便是这种复制也相对较快。其中的关键在于,由全局向私有内存复制第一数组行元素,代价最大的就是相干法;而与计算输出矩阵行的主双精确度循环的运行时相比,复制的间接成本算是相当适中了。
内核代码(主循环中被注释掉的代码是之前版本中已有的内容):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 6. 工作单元私有内存中带有第一矩阵行的内核。
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
CPU 吞吐量还保持与上一次大致相同的水平,而 GPU 吞吐量则回到曾达到过的最高水平,但处于新能力中。注意:CPU 吞吐量就像是被当场冻结了一样,只是有些微的不稳定;而 GPU 吞吐量则是大幅飙升(尽管不都是这样)。
我们要说明一点,实际的算术吞吐量会稍高一些,因为是将第一矩阵的行复制到私有内存中,所以现在执行的运算比以前更多。但是,它对最终吞吐量的估算影响不大。
源代码请见 matr_mul_row_in_private.mq5。
2.7. 将第二数组的列迁移至本地内存
现在,下一步要做什么就不难猜到了。我们已经采取了相应的步骤,隐藏与输出及第一输入矩阵关联的延迟。还剩下第二矩阵。
对于矩阵相乘中使用的无向积的更加细致的研究显示:在计算输出矩阵行的过程中,组内的所有工作单元均通过该设备对来自第二相乘矩阵相同列的数据进行重新优化。如下图所示:
图 16. 将第二矩阵的列迁移到工作组的 Local Data Share (本地数据共享)
如果构成工作组的工作单元在输出矩阵行开始计算之前,就将第二矩阵的列复制到工作组内存,那么从全局内存迁移的间接成本也会缩减。
这要求对内核和主机程序做出改动。最为重要的改动,就是针对每个内核设置本地内存。它应为显式,因为 OpenCL 中不支持动态内存分配。所以,足够大小的存储对象要首先置入主机,以供于内核中进一步处理。
只有这样在执行内核时,工作单元才会将第二矩阵的列复制到本地内存。而这是利用工作组所有工作单元循环迭代的循环分布并行完成的。但是,所有复制都要在该工作单元开始其主运算(计算输出矩阵行)之前完成。
正因如此,下述命令也要在负责复制的循环之后插入:
barrier(CLK_LOCAL_MEM_FENCE);
这是确保组内工作单元可以“看到”与其它单位协调、处于某特定状态的本地内存的一个“本地内存屏障”。工作组内的所有工作单元,都要先执行直至该屏障的所有命令,才可以继续进行内核的执行。换言之,此屏障是工作组内各工作单元之间的一种特殊同步机制。
OpenCL 中未提供工作组之间的同步机制。
下图所示为活动的屏障图解:
图 17. 活动屏障图解
事实上,看起来似乎只是工作组内的工作单元严格同时执行了代码。这仅仅是 OpenCL 编程模型的一种抽象。
到目前为止,我们在不同工作单元上执行的内核代码还都不需要同步的运算,因为它们之间没有任何将在内核中以编程方式设置的显式通信;此外,它甚至都没有需要。但是,此内核中却要求同步,因为本地数组的填充过程是在工作组的所有单位之间并行分布。
换句话说,每个工作单元都会将其值写入本地数据共享(此处为数组),而无需知道其它工作单元在此写入过程中还有多远。这里设置一个屏障,这样在有必要之前(即在完全生成一个本地数组之前),某特定的工作单元不会继续此内核的执行。
您要明白,该优化很难对 CPU 上的性能产生什么有益的影响:据 Intel 的《OpenCL 优化指南》称:在 CPU 上执行某内核时,所有的 OpenCL 内存对象均由硬件缓存,所以使用本地内存的显式缓存只是增加了不必要(但适度)的间接成本。
这是值得一提的另一个要点——它耗费了本文作者大量时间。它关系到一个事实:局部变量不能在内核函数头中(即编译阶段时,在该终端开发人员构建的当前实施中)传递。其背后的原因在于,为了将内存作为内核函数自变量分配给某个内存对象,我们必须首先利用 CLBufferCreate() 函数在 CPU 内存中显式创建该对象,并作为一个函数参数显式指明其大小。此函数会返回一个内存对象句柄,而该句柄则会进一步存储于全局 GPU 内存中,因为这里是它唯一的容身之处。
但是,本地内存是与全局内存不同的一种类型,所以创建的内存对象不能置入工作组的本地内存中。
功能齐全的 OpenCL API 允许显式分配所需大小的内存,且指针 NULL 会指向内核的自变量,即便是未如此 (CLSetKernelArg() 函数创建内存对象)。然而,CLSetKernelArgMem() 函数作为全功能 API 函数的 MQL5 仿真,其语法不允许我们在未创建内存对象本身的情况下,向其传递已分配给自变量的内存大小。我们可以向 CLSetKernelArgMem() 函数传递的,只是已于全局 CPU 中生成的、以及旨在向全局 GPU 内存迁移的缓冲区句柄。这里有一个悖论。
幸运的是,此内核中还有一种使用局部缓冲区的同等方式。您只需利用 __local 修饰符在内核主体中声明该缓冲区即可。这种情况下,分配到此工作组的本地内存,会在运行时(而非编译阶段)期间被确定。
而内核中继屏障之后出现的命令(代码中的屏障线以红色标示)从本质上来讲,与之前优化过程中的相同。主机程序代码仍相同(源代码请见 matr_mul_col_local.mq5)。
新的内核代码如下:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 7. 被迁移到工作组本地内存的第二数组的列
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
两种情况都显示出了性能劣化,只是不太严重。通过更改工作组的大小,来提高(而非劣化)性能是很可能的。最好将上例作为不同用途 - 说明如何使用本地内存对象。
关于使用本地内存时性能下降,有一种假设可以解释。大约 2 年前,habrahabr.ru 上发表了 《CUDA、GLSL 及 OpenMP 同 OpenCL 的对比》 (俄语)一文,文中称:
换句话说,这是否意味着 2 年前发布产品的本地内存不比全局内存快呢?上文发表的时间表明:在两年之前,Radeon HD 58xx 系列显卡已经面世,但根据作者的说法,还远未完善。我很难相信这一点,尤其是在 AMD 已推出轰动一时的 Evergreen 系列的情况下。我愿意利用更新的显卡来检验一下,比如 HD 69xx 系列。
补充:开启 GPU Caps Viewer (GPU 效能查看器),您会在 OpenCL 选项卡中看到下述内容:
图 18. HD 4870 支持的主要 OpenCL 参数
CL_DEVICE_LOCAL_MEM_TYPE:全局
语言规范中提供的此参数的阐释(表 4.3,第 41 页)如下:
支持的本地内存类型。可以设置为 CL_LOCAL,表明是专用的本地内存存储,比如 SRAM 或 CL_GLOBAL。
由此,HD 4870 本地内存确实是全局内存的一部分,而且该显卡中的任何本地内存操作都因此不再有用,而且不会导致任何快于全局内存情况的发生。此处是另一处链接,其中包括 AMD 专家针对 HD 4xxx 序列这一方面的澄清。这并不一定就是说您的显卡有多糟糕;只是告诉您硬件相关的此类信息可以在哪里找到 - 这种情况下,是在 GPU Caps Viewer 中。
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
最后,我们通过显式完成内核的向量化,来添加几画点睛之笔。于第一数组的行迁移到私有内存阶段衍生的内核 (matr_mul_row_in_private.mq5) 会充当初始内核,因为它似乎是最快的。
2.8. 内核向量化
为避免混淆,最好将此操作划分成多个阶段。在最初的修改中,我们不会更改内核外部参数的数据类型,只会向量化内部循环的计算:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 8. 采用 float4 的内核的部分向量化(仅内部循环)
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
出人意料的是,即便是这种初步的向量化,也在 GPU 上实现了很好的结果;尽管不算太大,但增益似乎仍有 10% 左右。
继续内核中的向量化:将“代价昂贵”的 REALTYPE4 向量类型转换操作,连同显式向量分量的规格一起,传送到填写私有变量 rowbuf[] 的外层辅助循环。内核中仍无变化。
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 9. 摆脱内核主循环中“代价高昂”的类型转换操作
注意:内层(及辅助)循环计数器的最大计数值已经低了 4 倍,而现在第一数组要求的读取操作比之前少了 4 倍 - 读取已经明确成为了一个向量操作。
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================算术吞吐量:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
可以看出,CPU 性能方面的变化相当大,而对于 GPU 而言,几乎就是革命性的变化。源代码请见 matr_mul_vect_v2.mq5。
我们仅利用宽度为 8 的向量来执行与内核上一变量相关的相同操作。作者的决定可以用 GPU 内存带宽为 256 位 (即 32 字节 8 个浮点型数字)来解释;因此,8 个浮点数据的同时处理(等同于 float8 的并行使用)似乎就自然而然了。
请牢记:这种情况下,COLSROWS 值应该可以被 8 整除。这一要求很正常,因为更精细的优化会对数据设置更具体的要求。
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
列表 10. 使用宽度为 8 的向量执行的内核向量化
我们必须在内核代码中,插入允许计算宽度为 8 向量的无向积的内联函数 dot8()。在 OpenCL 中,标准函数 dot() 仅可计算宽度不超过 4 的向量的无向积。源代码请见 matr_mul_vect_v3.mq5。
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
结果出人意料:CPU 上的运行时几乎比之前短了两倍,而 GPU 上的运行时却稍有加长,尽管 float8 对于 HD 4870 来讲,总线宽度已经足够(等同于 256 位)。这里,我们要再一次求助于 GPU Caps Viewer。
相关阐释请见图 18 参数列表的倒数第二行中:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
查阅《OpenCL 规范》,您就会在第 37 页表 4.3 的最后一列看到下述有关此参数的文本:
可以放入向量的内置标量类型的首选朴素向量宽度尺寸。向量宽度被定义为可以存储于该向量中的标度元素的数量。
由此,对于 HD 4870 而言,向量 floatN 的首选向量宽度为 float4 而非 float8。
我们就在这里结束内核优化周期吧。我们还能讲到更多内容,只是限于本文篇幅,就不再深入讨论了。
本文讲述了一些优化能力,但至少要对此内核借以执行的基本硬件多少有些了解,才能启动这些能力。
获取的数据远非最高值,但即便是这样,也建议充分利用现有资源(由该终端开发人员实施的 OpenCL API 不允许控制对于优化而言很重要的一些参数 - 尤其是工作组的大小),通过主机程序执行获得的增益是非常可观的:GPU 上执行的增益,与 CPU (尽管未充分优化)上的顺序程序增益的比率约为 200:1。
我真心地感激 MetaDriver,感谢其提供的宝贵建议,在我还没有独立 GPU 的时候给我利用它的机会。
随附文件目录:

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
