振荡器代表指标的一个子类,该指标围绕中心线在预设的水平内上/下波动。 它们在技术分析中广泛用作交易事件的生成器,例如,当与中心线交叉,或超过某个阈值时。 MACD、RSI、CCI 是常见的振荡器指标,每个振荡器指标都有其独有的特征,例如尝试通过搜索价格的变化率(也称为动量)或寻找主要趋势来预期逆转。
通常,按公式计算两个瞬时之间价格差值的振荡器表现出价格超前 行为(例如 RSI、CCI),而基于均值的振荡器则表现出滞后行为。 举一个相关的例子,MACD 是根据两个均值之间的差值计算得出的,因此可以认为 MACD 同时表现出超前和滞后特性。 依据差值绘图则呈现为直方图的形式,令中心线交叉和发散易于发现。
尽管如此,使用各种振荡器都是利弊互现,因为行情条件变化会增加假信号(尤其是对于超前振荡器),或快速发散,这些都可能会令大多数风险/回报率产生扭曲(滞后振荡器通常会发生这种情况)。 凭经验,交易者每次观察多个振荡器可能是比较明智的选择,如此会得到更多独立的交易信号确认。
在本文中,将介绍“轴心均值振荡器”,它直接派生自累积移动平均值(CMA),尝试为振荡器全景图引入一些新功能。
在统计数据中,移动平均值(MA)也称为简单均线,是取时间序列最后 n 个数据进行平均计算。 当输入新值时,最旧的数值根据先进先出(FIFO)策略遭丢弃。均线价位在金融设定中很有用,因为它们在下跌行情中可以解释为支撑,而在上涨行情中可以解释为阻力。
均线从概念上讲是在固定内存的缓冲区上工作的,它会舍弃比最后界定期限更古老的数据(以及一些信息片)。 如果理想情况下,我们将此类缓冲区扩展到无限大,如此即可计算直至当前界定期限为止的所有数据,于是我们得到了 CMA。
幸运的是,在实际应用中,我们不需要分配无限的内存来存储每个单一界定期限! 实际上,可以用很少的变量来计算 CMA(取决于是否使用递归公式,有关详细信息,请参见下图)。
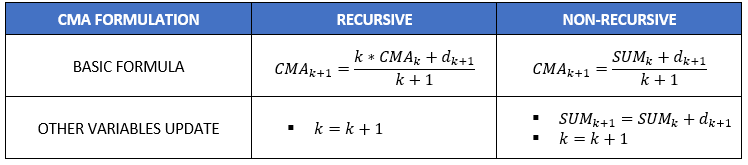
表 1: CMA 的两个公式。
CMA 公式的第二个有趣方面是计数器的存在,该计数器每次递增一个单位。 这意味着下一个 CMA 值是合成的,一部分是完全可预测的元素,且与其他信息互补,可用于预测目的。 例如,在横盘行情下,价格将趋向于 CMA 数值。
CMA 是下文介绍的 PMO 的基本成分。
PMO 建立在常规化指数(我们称为轴心均值(PM))的基础上,该常规化指数是计算最后界定期限和 CMA 之间的分值。
PM 提供了价格与 CMA 的距离 的快速量化解读。 这意味着可以将 PM 视为扩散的量度。 例如,PM 值为 1.0035 仅表示当前值比 CMA 高 0.35%,而 PM 等于 1 则表示当前值与 CMA 完全一致。
鉴于可以为每个数据点重复计算 PM,这意味着每个时间序均可列转换为 PM 信号。 最终,我们将 PMO 定义为两条 PM 信号均线之间的差值。 简而言之,PMO 提供了两条扩散之间差值的度量,因此在交易环境中查看其应用很价值。
既可在相同的 PM 信号上,亦或在两个不同的 PM 信号上计算两个 PMO 的均值。 在本文中,我们考虑分别应用收盘价和开盘价数据获得的 PM 信号的简单均线。

表 2: PM & PMO 公式。
尽管存在相似之处,但此处介绍的 PMO,其体现形式与 MACD 在几个方面存在不同。 MACD 通常应用于价格信号,而 PMO 信号的底层则是 PM。 甚而,虽然在 MACD 中考虑到指数均值,但在此我们只关注简单均值,而将更复杂 PMO 的变体留给该主题的未来工作。
PMO 很少需要直接从其公式中派生出的输入:
//--- input parameters input datetime startingTime; input int MA_close=3; input int MA_open=21;
总共,我们将用到三个缓冲区:
//--- indicator buffers double PMOBuffer[]; double closeBuffer[]; double openBuffer[];
至于所关注的全局变量,必须有一个计数器和两个变量来存储 PMO 计算的收盘价和开盘价之和。 我们还添加了两个其他支持变量,以便跟踪自输入开始时间以来所有缓冲区都要用到的第一个指数。
//----global vars--- int counter=1; double sum_close=0; double sum_open=0; bool first_val_checked; int first_valid_index;
为了支持计算 PMO 的两个均值,必需实现一个计算均值的函数。 必须避免的唯一障碍是在开始时间附近,缓冲区的最开始执行计算的情况。 此刻,没有足够的元素可用于计算。 不过,由于 PM 的定义,我们可以假设将启动时间之前的值设置为 1,从而令均值计算没有任何滞后。 因此,支持函数如下:
double simpleMA(const int pos, const int avg_positions, const double &data[],int arr_tail_pos){ double _local_sum = 0; for(int i=pos+avg_positions-1; i >= pos;i--){ if(i > arr_tail_pos){ _local_sum += 1; // when requested data exceed buffer limit set trailing 1s }else{ _local_sum += data[i]; } } return _local_sum/avg_positions; }
所有内容均已提供,我们终于可以看一下程序核心:
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- ArraySetAsSeries(PMOBuffer,true); ArraySetAsSeries(closeBuffer,true); ArraySetAsSeries(openBuffer,true); ArraySetAsSeries(open,true); ArraySetAsSeries(high,true); ArraySetAsSeries(time,true); //--- return value of prev_calculated for next call int total = rates_total - prev_calculated; double _tmp_sum_close,_tmp_sum_open; if(total > 0){ for(int i=total-1;i>=0;i--){ if(time[i] >= startingTime){ if(first_val_checked == false){ first_val_checked = true; first_valid_index = i; } sum_close += close[i]; sum_open += open[i]; closeBuffer[i] = close[i] *counter / sum_close; openBuffer[i] = open[i]*counter / sum_open; PMOBuffer[i] = simpleMA(i,MA_close,closeBuffer,first_valid_index)-simpleMA(i,MA_open,openBuffer,first_valid_index); counter++; } else{ PMOBuffer[i] = 0; } } }else{ _tmp_sum_close = sum_close +close[0]; _tmp_sum_open = sum_open + open[0]; closeBuffer[0] = close[0] *counter / _tmp_sum_close; openBuffer[0] = open[0] *counter / _tmp_sum_open; PMOBuffer[0] = simpleMA(0,MA_close,closeBuffer,first_valid_index)-simpleMA(0,MA_open,openBuffer,first_valid_index); } return(rates_total); } //+------------------------------------------------------------------+
在此,我们提供了一些在 EURUSD 图表上运行 PMO 所获得的实验结果和注解。 将讨论两个主要主题:
交易层面
如图所示,PMO 和 RSI 之间有极大的相似之处:这两个信号几乎重合。 但是,也存在一些差异。 主要转折在 9 月份附近。 2019 年 9 月 12 日(结合欧洲中央银行的一些官方通讯),细心的读者可能会在 PMO 上看到 “M” Merril 形态,其左肩高于右肩,而 RSI 信号和相关的 EURUSD 价格发生的情况恰好相反。 这是由于价格上涨发生在 9 月。 相对于 CMA,12 日高于第二天观察到的 CMA。 这条信息对于在第二个高峰之后的空头持仓很有用。
与 RSI 的相似之处,我们可以在超买和超卖情况下围绕高峰和低谷考虑逆转,因此可以作为交易策略的早期信号。 尽管 PMO 不受 RSI 的限制,但与零中心线的直接交叉可视为趋势的进一步确认。 如引言中所述,交易成功的良好做法可能就是一次性组合多个信号。
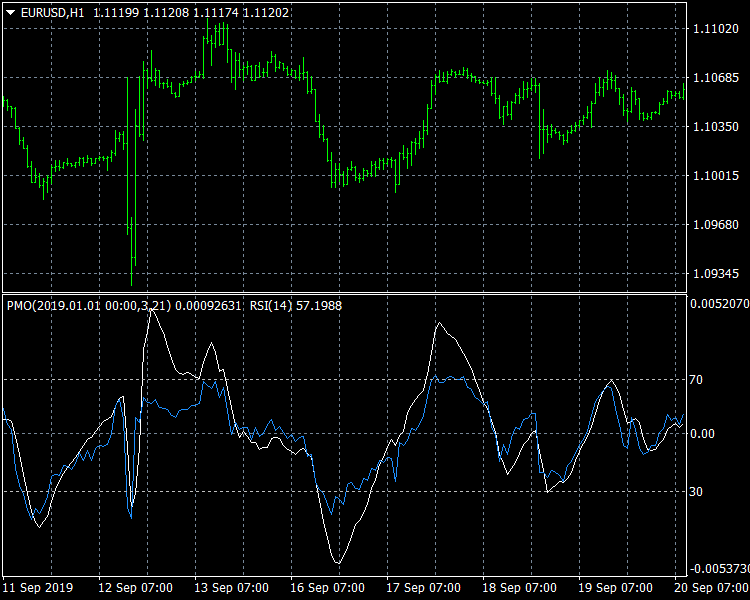
图例 1: PMO(3,21)和 RSI(14)之间的相似之处。
现在,我们能够为运用 PMO 进行交易草拟一套非常基本和简化的“如是 - 则(IF THEN)”规则,从而为基于 PMO 的智能交易系统的未来开发留出更为复杂的策略。
针对行情变化条件的快速响应是成功交易的关键因素:使用均线时,信号越平滑,延迟就越大。 使用 PMO( m,n) 时,m 为振荡器的滞后,而 n 与中心线的交叉滞后有关。 当然,PMO 最快的响应是通过 PMO(1,1) 获得的,这意味着我们可以计算两个 PM 之间的差,而完全不用计算均值。 一个良好的折衷办法是使用 PMO(1, n),其中 n 较小(例如 5),这样可以保证最快的响应速度,以及与零中线交叉不会太滞后。
现在查看零中心线附近的 PMO 值分布很有用。 如本文定义的那样,PMO 不受 RSI 限制,因此分析 PM 值高于或低于某些阈值的可能性也许会很有趣。
下图显示了在 EURUSD 图表上运行 PMO(3,21) 获得的结果,其 H1 时间帧涵盖了 2019 年的前 8 个月。 PMO 值以零为中心形成钟形分布。 轻微的左偏斜可能是由于 EURUSD 过去几个月累积的空头持仓过多。 尽管如此,在零附近的对称性优势,可令我们推断出短线和长线走势之间存在总体平衡。
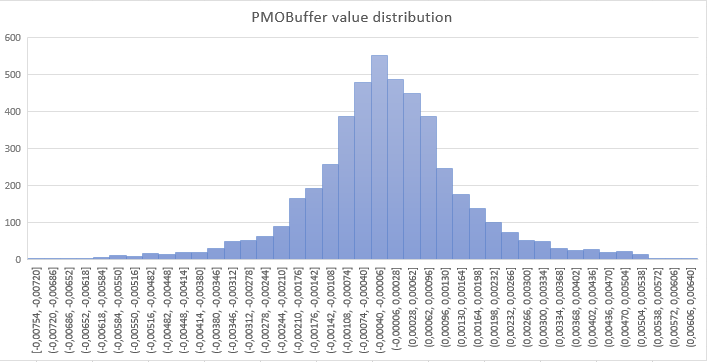
图例 2: PMO(3,21) 数值的分布类似于钟形曲线。 这令我们推测一个准高斯统计模型对于预测目的是有益的。
要考虑的另一个层面是 PMO 和直接根据收盘价和开盘价信号计算的移动平均值之间的关系,而非依据其 PM 对应值。 如下图所示,发现黏合附近 R 平方有很强的相关性。 这意味着处理 PM 信号不会令底层信号失真。 与此同时,由于 PM 计算操作的标准化,据 PM 信号操作还拥有比较不同来源(例如其他货币对)结果的优势。
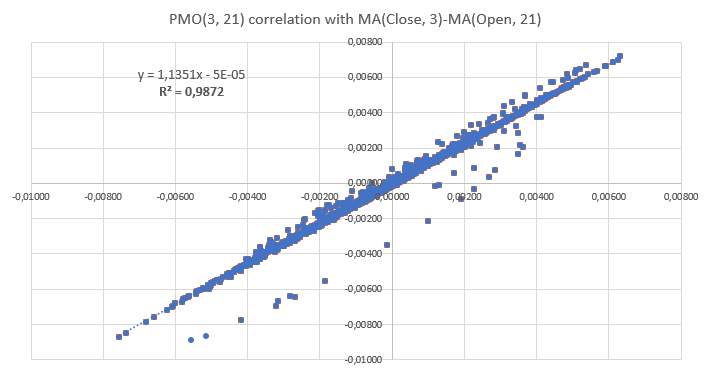
图例 3: PMO(3,21) 与其非常规化版本之间观察到相关性。 获得的几乎呈线性的形状表明,PMO 中采用的常规化在解释底层开盘价和收盘价信号时不会出现重大失真。
在本文中,我介绍了轴心均值振荡器(PMO),它是基于新颖的轴心均值(PM)概念实现的累积移动平均线(CMA),可作为 MetaTrader 平台的交易指标。 所拟议的振荡器与 RSI 或 MACD 等其他众所周知的振荡器相似,但由于使用 CMA,从而具有一些特殊性。 在进一步开发方面,仍有许多工作要做,诸如:基于其他类型平均值的变体,举例来说,基于 PMO 值围绕零中心线的统计分布信息制作的智能系统。
鼓励读者利用所附的文件自行实验。
| 文件 | 说明 |
|---|---|
| PMO.mq4 | 本文所用 PMO 的 MQL4 源代码。 |
| PMO_logger.mq4 | 拥有日志功能的 PMO 数据分析 MQL4 源代码。 实现了两个附加输入:data_logging(true / false 标志)和 filename(字符串)。 |
| PMO.mq5 | PMO 的 MQL5 源代码 |
| PMO_logger.mq5 | 拥有日志功能的 PMO 数据分析 MQL5 源代码。 实现了两个附加输入:data_logging(true / false 标志)和 filename(字符串)。 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...