研报名称：《选股因子系列研究（二十五）——高频因子之已实现波动分解》

研报作者：海通证券 冯佳睿 袁林青

在系列前期报告中（《选股因子系列研究（十九）——高频因子之股票收益分布特征》），我们基于股票高频收益分布特征对于相关因子的选股效果进行了回测。研究发现，股票高频偏度具有较好的选股效果，但是高频方差以及高频峰度并无显著的选股能力。

考虑到股票日收益的波动率同样选股效果不佳，但将其拆分为系统波动以及特质波动后，两个因子皆具有较好的选股效果。本报告尝试对于股票高频波动率进行拆分，并期望从高频波动中提取出有效的选股因子。

“系统波动 特质波动”的拆分方式在高频维度上无法得到具有优秀选股效果的因子。在1分钟的数据频率下，高频特质波动率因子表现较差，并无明显的选股能力。随着数据间隔的增大，该因子的RankIC、ICIR以及多空收益都出现了改善。
?

“上行波动 下行波动”的拆分方式在高频维度上选股效果较好。上行波动率因子在不同的数据频率下皆展现出了一定的选股效果，即前期股票高频上行波动越大，未来1个月收益表现越差。将上行波动率对于股票波动率进行调整后可计算得到上行波动占比，该因子在不同的数据频率下皆具有较好的选股能力。1分钟数据频率下，因子月均IC达-0.083，ICIR为-3.9，月度多空收益为1.89%。
?

“系统波动 特质波动”的拆分得到的高频因子在正交后基本无选股效果残留。
?

上行波动占比因子在正交后依旧具有显著选股能力，且数据频率越高因子选股效果越好。在1分钟频率下，正交后的上行波动占比因子的IC为-0.038，ICIR为-3.6，月度多空收益达0.92%。
?

上行波动占比因子在加入到多因子模型后能够对模型产生进一步的提升。加入1分钟上行波动占比的改进模型，相比于原始模型在复合因子的IC、ICIR、月度胜率以及月度的多空收益上，都有进一步的提升。
?

2017年以来因子截面选股效果较好，仅在6月失效。除了6月外，该因子在其他月份上的IC以及月度多空收益皆为正。虽然该因子在17年对于股票收益有着较好的区分效果，但是无法通过该因子构建单因子组合获取正向收益。

报告第一部分讨论了因子的构建以及因子的选股能力。第二部分从正交因子的角度对于因子的选股能力进行了分析。第三部分对比分析了加入高频因子的改进模型以及未加入高频因子的原始模型。第四部分展示了相关因子2017年以来的表现。

高频波动率的分解

系列前期研究（《“双面”波动率——波动率因子的分解与截面收益》）发现，通过对于波动率进行分解，可从中提取出具有较好选股效果的因子。因此本报告将先尝试从“系统波动 特质波动”的角度对于股票高频收益波动进行分解，并对于分解得到的因子的选股效果进行回测。

高频收益波动分解——“系统波动 特质波动”

对于“系统波动 特质波动”这种拆分方式，投资者需要通过Fama-French回归将股票收益分解为系统收益与特质收益，然后再计算系统收益与特质收益的波动。具体回归方程如下所示：

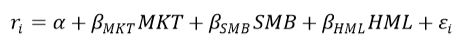
其中，ri为股票收益，MKT为市场收益，SMB为市值溢价，HML为估值溢价，回归残差为股票特质收益。对于高频收益序列也可做类似回归处理，回归因变量为股票高频收益序列，自变量为MKT、SMB以及HML的高频收益序列。其中，回归残差为股票高频特质收益。也即，对于特定时间段的股票i的高频收益序列{ri}，股票高频系统波动、高频特质波动以及高频特异度可定义为：

由于本报告旨在考察因子在月度上的选股效果。故对于任意股票，使用其过去一个月的高频收益序列进行回归并计算对应因子值。

为了体现数据频率对于因子效果的影响，本报告分别使用1分钟、5分钟以及10分钟频率下的股票收益序列进行了因子计算。下表展示了2010年以来，高频系统波动、高频特质波动以及高频特异度的月度选股效果。

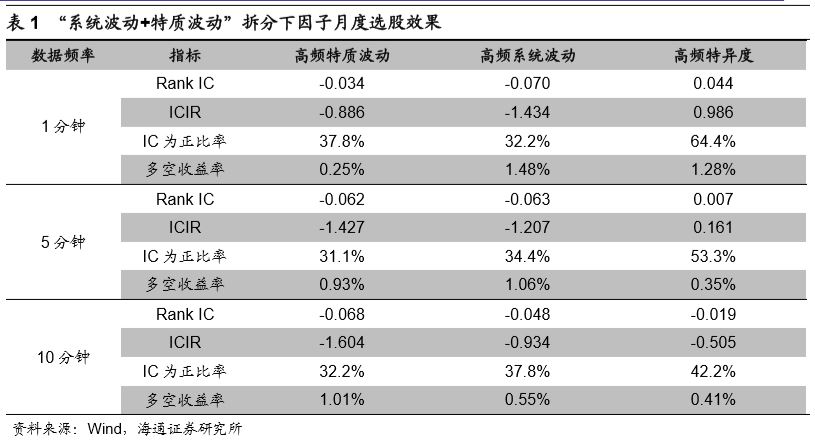
上表从RankIC、ICIR、月度胜率以及月度多空收益率的角度对于因子表现进行了评价。不难发现，“系统波动 特质波动”这种拆分方式并不适用于股票高频收益序列。在1分钟的数据频率下，高频特质波动率因子表现较差，并无明显的选股能力。随着数据间隔的增大，该因子的RankIC、ICIR以及多空收益都出现了改善。因此我们有理由推断，随着数据间隔的进一步扩大，因子的选股效果会逐步回复至日级别的水平。下图展示了1分钟、5分钟以及10分钟数据频率下高频特质波动率因子的分组收益特征。

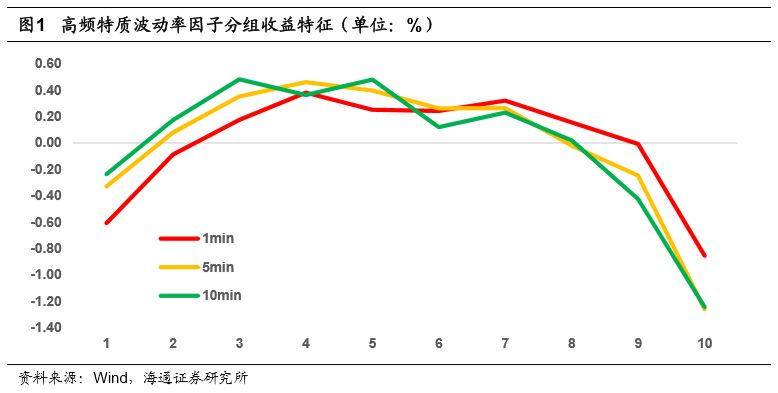
此外，日级别上选股效果极为稳定的特异度因子，在高频维度上的选股效果也不佳。

高频收益波动分解——“上行波动 下行波动”

由于“系统波动 特质波动”的分解方式在高频数据上并未取得较好的结果，本部分尝试从“上行波动 下行波动”的角度对于股票高频波动进行分解。对于某股票i在某段时间上的高频收益序列，其上行波动及下行波动的计算方式如下所示：

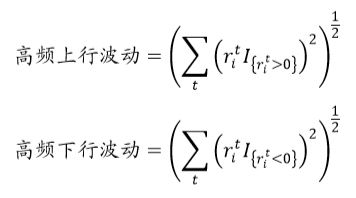
类似地，可定义股票i上行波动占比与下行波动占比，计算方式如下所示：

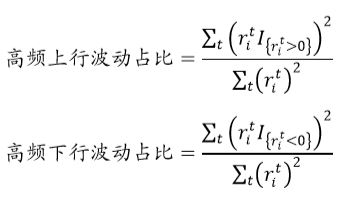
同样使用过去一个月的1分钟、5分钟以及10分钟收益序列计算因子值。下表展示了2010年以来，上行波动、下行波动、上行波动占比的因子月度选股效果。由于截面标准化后，上行波动占比因子与下行波动占比因子的线性相关性为-1，故而下表仅展示上行波动占比因子的选股效果。

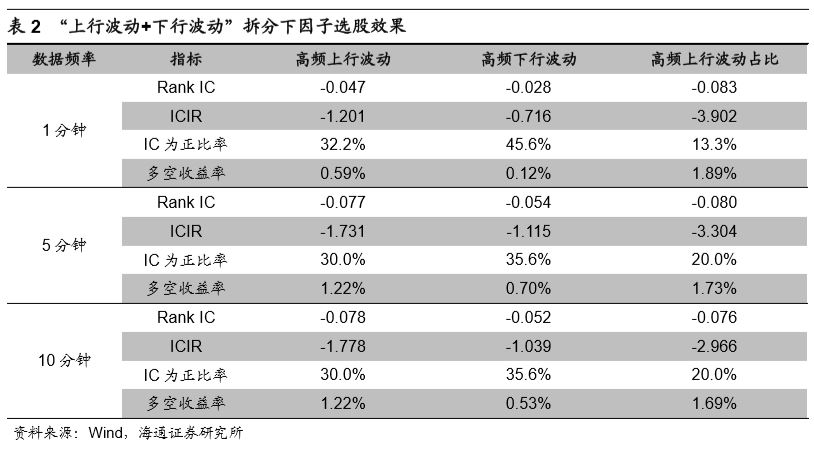
上行波动率因子在不同的数据频率下皆展现出了一定的选股效果，即前期股票高频上行波动越大，未来1个月收益表现越差。根据相关文献的解释，股票高频收益的上行波动衡量了股票价格拉升的特征。假设有两只股票在过去一段时间有着相同的涨幅，其中一只股票的涨幅由持续稳定的小幅上涨累计带来，而另一只股票的上涨源自于股票短期的大幅拉升。那么后者更有可能在收益上出现反转，而后者在因子值上也会体现出较高的上行波动率。

将上行波动率对于股票波动率进行调整后，可计算得到上行波动占比。该因子在不同的数据频率下，皆具有较好的选股能力。1分钟数据频率下，因子月均IC达-0.083，ICIR为3.9，月度多空收益为1.89%。下图展示了该因子在不同数据频率下的分组收益情况。

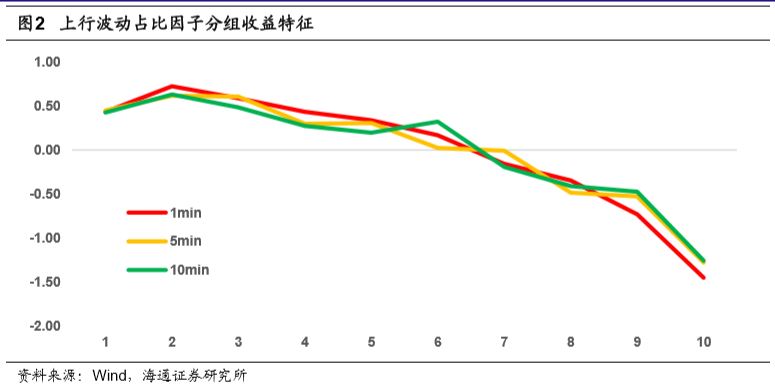
由上图可见，该因子在不同数据频率下，对于股票下一个月的收益都有着较好的区分效果。

上行波动占比分组特征分析

由于上行波动占比呈现出较好的选股效果，我们不得不怀疑因子的选股效果是否来源于现有的选股因子。因此可以使用该因子对于股票进行分组，并统计不同分组股票因子的特征。

下图展示了使用1分钟上行波动占比因子从小到大排序，得到的分组股票（横轴的1-10组）的相关特征。（收益、市值、换手、反转、日级别特异度）

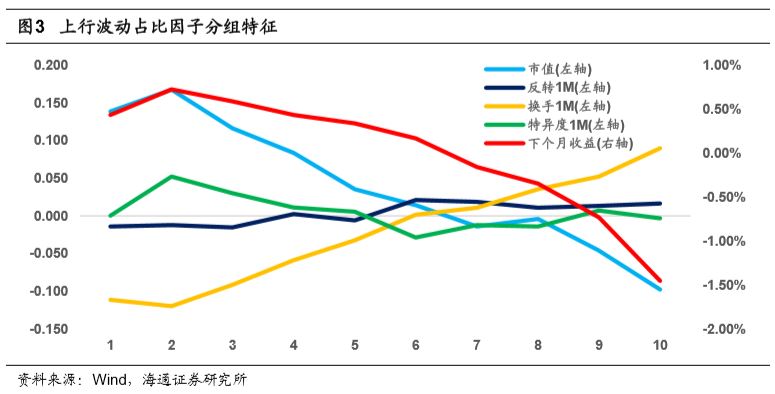
观察上图可知，上行波动占比因子和市值以及换手因子具有较强的相关性，因子多头组合（第1组）呈现出低换手、大市值的特征。因此可以推断，该因子的选股效果并不是来源于市值因子而是来源于换手率因子。此外，上行波动占比和日级别特异度因子以及反转因子相关性较低，组间特征单调性较弱。

因子正交分析

考虑到高频因子与常见因子的相关性，本节对于“系统波动 特质波动”以及“上行波动 下行波动”分解得到的因子进行正交化处理，并对于正交后的因子的选股效果进行回测。

在正交处理中，本章剔除了行业、市值、非线性市值、换手、反转、日级别特异度、估值、成长以及盈利的影响。（详细处理细节可参考专题报告《选股因子系列研究（十七）——选股因子的正交》）

正交处理——“系统波动 特质波动”

下表展示了正交后的高频系统波动、高频特质波动以及高频特异度的选股效果。

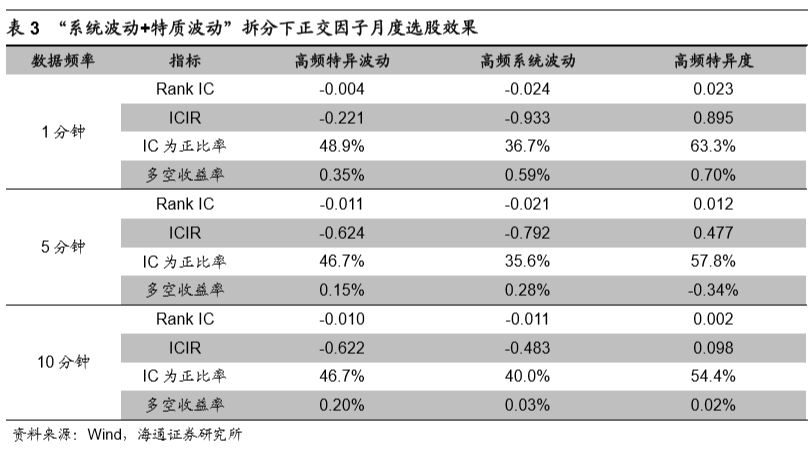
在剔除了常见选股因子的效果后，该类因子在各数据频率下已无选股能力，因子在RankIC、ICIR以及月度多空收益上的表现较差。

正交处理——“上行波动 下行波动”

下表展示了正交后的高频上行波动、高频下行波动以及高频上行波动占比的选股效果。

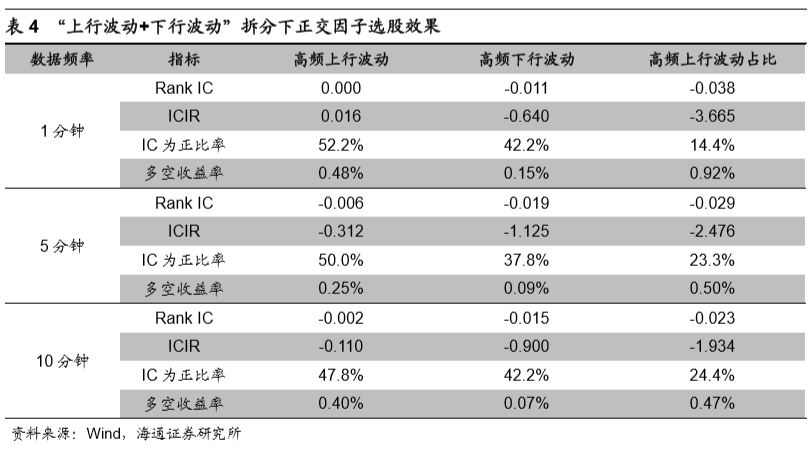
在剔除了常见选股因子的效果后，上行波动占比因子依旧呈现出了显著的选股效果，而且因子选股效果随着数据间隔的缩短而逐渐变强。

在1分钟频率下，正交因子的IC为-0.038，ICIR为-3.6，多空收益达0.92%。因子的选股效果之所以随着数据间隔的缩短而逐渐增强，是因为上行波动占比衡量了股票大幅拉升的特征，而这种特征在数据间隔较短的情况下更容易被识别。

结合上行波动占比因子的原始选股效果以及正交选股效果，我们认为该因子可以被放入多因子模型进行进一步的分析。

多因子模型对比分析

由于新因子的研究最终还是要服务于多因子模型，所以本章主要讨论上行波动占比因子在加入多因子模型后对于模型的影响。

首先，我们会从回归法的角度讨论因子在加入模型后是否具有显著的选股效果。其次，我们会从复合因子的角度观察因子在加入多因子模型后对于模型表现的影响。最后，我们会对于该因子在多因子模型中所占的权重进行分析。

在进行模型对比时，原始模型为使用市值、非线性市值、换手、反转、特异度、估值、成长以及盈利因子，构建的最大化预期收益月度选股组合。其中，因子集合进行正交化处理。改进模型在原始模型的基础上，考虑加入各数据频率下的上行波动占比因子。

本章在进行最大化预期收益多因子组合构建时按照以下规则进行：

1）使用2010年1月至2017年7月间的数据进行回测；
2）每月月末计算因子值，并对因子统一进行截面标准化的处理；
3）分配因子权重时使用历史滚动24月的因子表现；
4）在调仓时，组合按照涨停不买、跌停不卖的规则进行；
5）调仓考虑双边千五的交易费用；
6）选股范围剔除ST股、上市不满6个月的股票。

Fama-MacBeth回归检验

使用2012年1月至2017年7月底之间的数据可分别对于原始模型以及改进模型进行Fama-MacBeth回归检验。由于模型由正交因子组成，所以任意新因子的引入并不会明显影响原有因子回归系数及其显著性。故而，我们可将注意力集中在新加入因子的回归系数及其T统计量上。

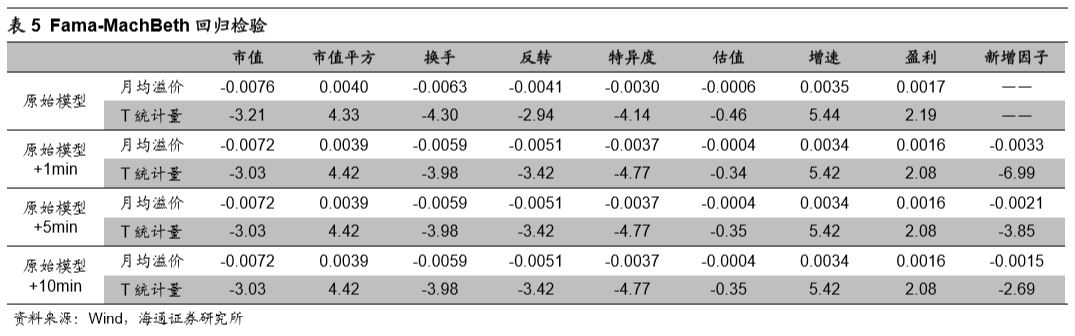
观察上表结果可以发现，1分钟频率下的上行波动占比因子选股效果最强，月均溢价达33bp，同期市值因子月均溢价为72bp，反转因子月均溢价51bp，日级别特异度因子月均溢价37bp。从显著性上看，上行波动占比因子在12年至17年7月间具有十分稳健的选股效果，因子月度溢价T统计量的绝对值接近7。随着数据间隔的增大，因子的月均溢价以及显著性都出现了减弱。此处结果与前文中正交分析的结果一致。

复合因子分析

基于前文提到的模型构成，可分别使用原始模型以及改进模型在2012年1月至2017年7月底间构建全市场月度选股模型。下表从复合因子、模型月度Top-Bottom10%多空收益以及TOP100选股组合的角度，对比了原始模型与改进模型的不同。在进行选股时，剔除上市不满6个月的股票、ST股以及无法交易的股票。

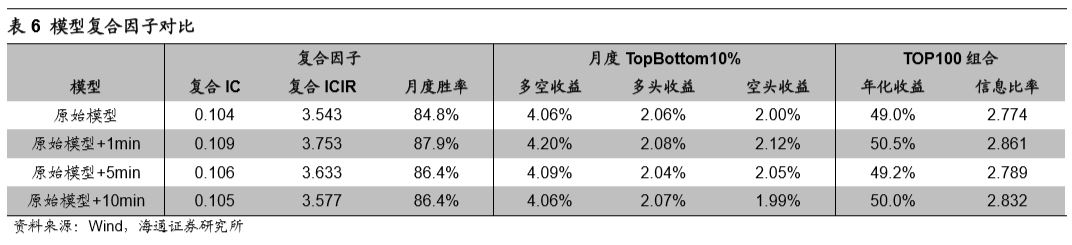
观察上表不难发现，加入1分钟上行波动占比的改进模型相比于原始模型产生全方位的改进，无论是复合因子的IC、ICIR、月度胜率还是月度的多空收益。对于全市场TOP100组合，改进模型也在年化收益以及信息比率上产生了一定的提升。

值得注意的是，虽然改进模型相比于原始模型有一定的提升，但是提升幅度较为有限。考虑到因子加权方式对于改进模型的提升效果有一定的影响，我们会在后一节中对于因子权重占比进行分析。

多因子模型因子权重分配情况

下图展示了加入1分钟频率的上行波动占比的多因子模型的权重分配情况。

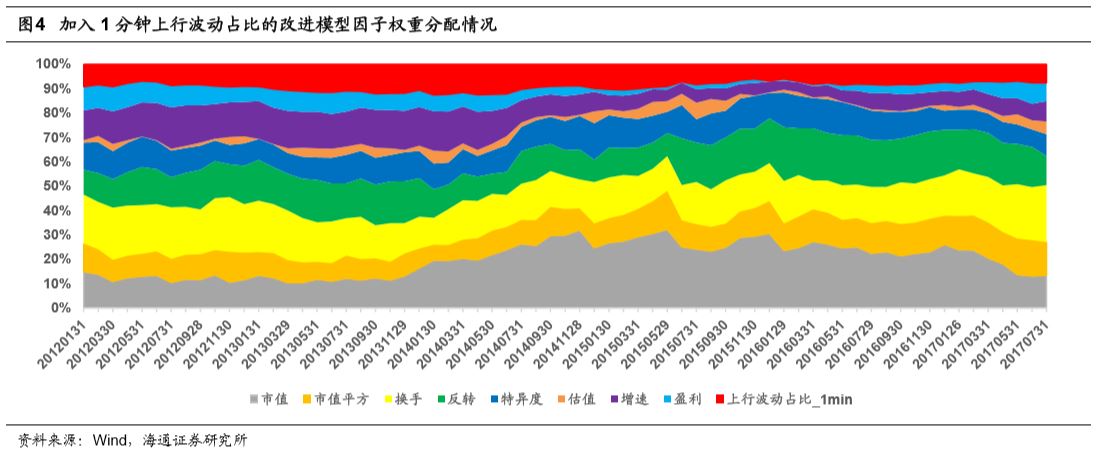
1分钟上行波动占比因子在模型里长期占有约10%的权重，同期，市值权重在15%~30%之间。由于5分钟上行波动占比以及10分钟上行波动占比选股效果较弱，故而这两个因子在对应多因子模型里面所占权重较低（见以下两图）

下图展示了加入5分钟频率的上行波动占比的多因子模型的权重分配情况，新加入因子在模型里所占的权重约为5%。

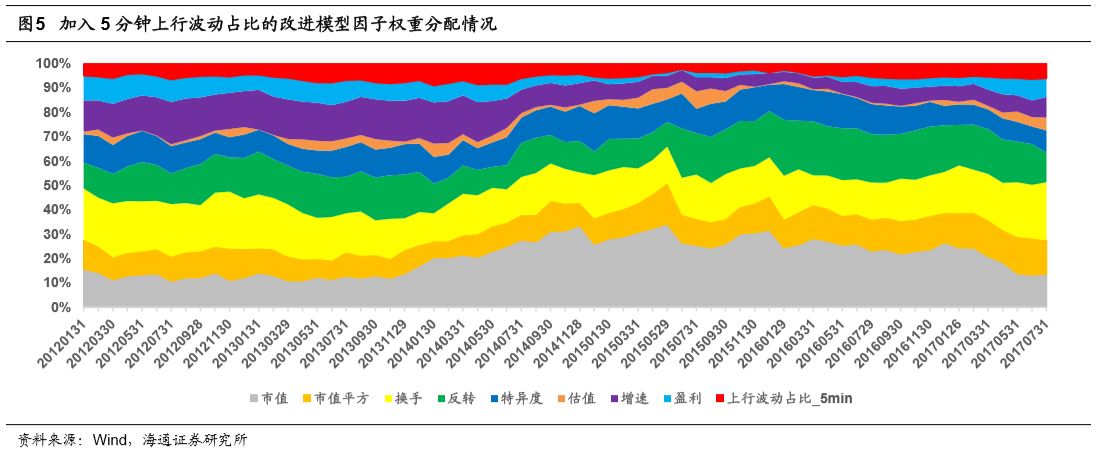
下图展示了加入10分钟频率的上行波动占比的多因子模型的权重分配情况，新加入因子在模型里所占的权重在3%与5%之间。

因子2017年以来的表现

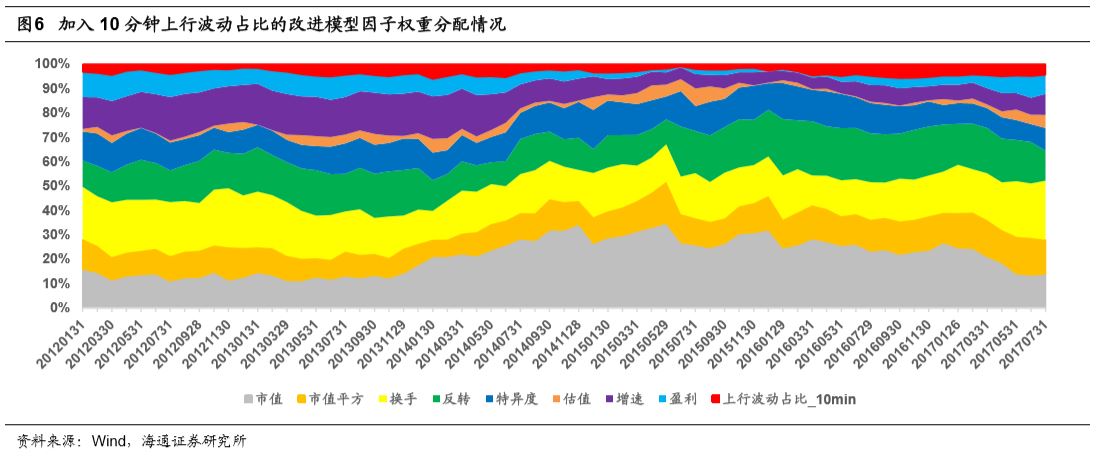
2017年以来市场风格出现了十分明显的切换，许多前几年有效的因子在2017年都出现了失效。下表展示了上行波动占比因子在2017年1月至7月间每月的多空收益以及IC情况。

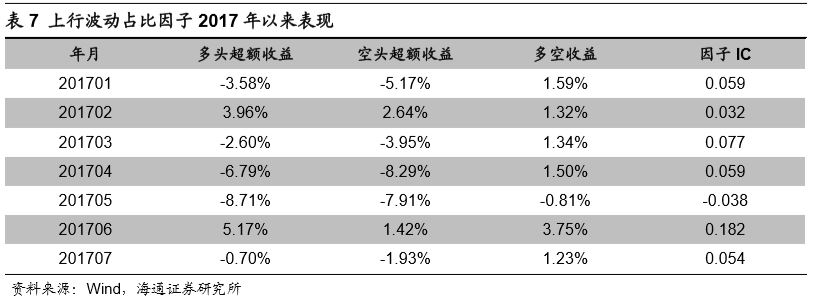
除了6月外，该因子在其他月份上对于股票收益都有着较好的区分效果。但遗憾的是，无法通过该因子构建单因子组合获取正向收益。使用上行波动占比因子构建得到的TOP10%多头组合，在17年以来的累计收益为-13.25%。

总结

在系列前期报告中（《选股因子系列研究（十九）——高频因子之股票收益分布特征》），我们基于股票高频收益分布特征对于相关因子的选股效果进行了回测。研究发现，高频波动因子并无显著的选股能力，故而本报告尝试对于高频波动因子进行提升。

研究发现，“系统波动 特质波动”这种在日级别上较为有效的拆分方式，在高频维度上并不能获得稳健的选股效果，而“上行波动 下行波动”这种拆分方式能够从股票高频收益波动中提取出有效的选股因子——上行波动占比。该因子在剔除了日级别常见选股因子的影响后，依旧具有较好的选股效果。