研报名称:《选股因子系列研究(十九)——高频因子之股票收益分布特征》
研报作者:海通证券 冯佳睿 袁林青
随着传统因子研究的深入,通过使用日级别数据已经很难发现能够在传统技术选股因子之外提供额外选股能力的因子了。考虑到传统因子多使用日级别数据刻画股票日间的形态特征,通过引入日内高频数据刻画股票日内的特征也许能够为模型带来新的信息以及Alpha。这一观点也在本系列前一篇研究(《选股因子系列研究十八——价格形态因子》)中有所印证。
本报告主要使用了股票1分钟价格数据构建了相关因子,对于股票高频收益分布特征(方差、偏度以及峰度)进行了刻画。报告主要分为三部分,第一部分讨论了因子的构建以及计算方式。第二部分从单因子的角度对于因子的选股能力进行了分析。第三部分对比分析了加入高频因子的改进模型以及未加入高频因子的原始模型的表现差距。
高频偏度因子在不同计算方法、不同数据频率下皆具有选股能力。不同频率、不同计算方式下因子的rankIC的绝对值基本维持在0.05~0.06左右,ICIR的绝对值普遍高于2.5,因子IC月度胜率接近80%。结合因子分组收益情况,我们认为高频偏度因子具有进一步研究分析的空间。
正交高频偏度因子同样具有选股能力。考虑到因子与换手率之间的相关性,本文对于高频偏度因子进行了正交化处理并剔除了行业、市值、非线性市值、换手、特异度以及反转因子的影响。正交后的高频偏度因子选股效果虽然有所减弱,但是因子依旧具有选股能力。1分钟的高频偏度因子IC绝对值下降至0.03附近,但ICIR绝对值依旧在2以上。5分钟高频偏度因子受到的影响较大,IC绝对值下降至0.02附近,ICIR绝对值在1.5~1.7之间。
从Fama-MacBeth回归检验来看,高频偏度因子具有额外选股能力。使用2010年1月至2017年3月底之间的数据可分别对于原始模型以及改进模型进行Fama-MacBeth回归检验。观察新增因子回归系数均值以及T统计量可知,各计算频率以及计算方法下的高频偏度因子在回测时间段中具有显著选股能力。此外,1分钟偏度因子选股效果强于5分钟偏度因子选股效果,这一点在回归系数绝对值以及回归系数T统计量绝对值大小上皆有所体现。
改进模型TOP100组合相比于原始模型TOP100组合改进幅度有限。在加入1分钟偏度因子后,TOP100纯多头组合在年化收益、收益回撤比以及信息比率上皆有所提升。在加入5分钟偏度因子后,部分改进模型在年化收益上并未出现改进,仅在收益回撤比以及信息比率上有所提升。
?
1分钟高频偏度因子打分权重略高于5分钟高频偏度因子。改进多因子模型中1分钟高频偏度因子权重占比约为10%,5分钟偏度因子权重占比约为5%
系列前期研究(《选股因子系列研究十八——价格形态因子》)发现,通过引入因子刻画股票日内形态可在现有因子外带来额外选股能力。相关海外研究也表明股票日内价格形态分布特征也对于股票未来收益具有一定预测作用。所以本报告使用了日内分钟级数据构建了相关因子刻画股票日内收益分布的方差、偏度以及峰度。考虑到数据频率对于因子的影响,本文在计算因子时分别使用了股票1分钟对数收益以及股票5分钟对数收益序列。
在任意交易日,基于股票i的高频收益序列{rij}对于市场上交易的股票可计算高频收益方差、高频收益偏度以及高频收益峰度三个指标。常见计算方法如下:
计算方法1

在任意选股时刻,股票的因子值为前N日指标的均值。考虑到在实际进行选股时往往都是月度选股,本报告在计算因子值时使用的是股票过去一个月的均值。考虑到计算方式对于因子的影响,本报告也尝试了使用另外两种不同的方式对于因子进行计算。
计算方法2

计算方法3
由于不同的日内时间段划分会对于收益序列产生一定影响,所以计算方法3的核心思路在于遍历所有时间段的划分,在不同划分下分别计算因子值并进行平均。

本节讨论了高频因子的构建,后文会在不同的数据频率以及不同的计算方式下对于高频方差、高频偏度以及高频峰度进行回测检验。最终我们希望能够在这三个高频因子中得到在不同频率和计算方法下都表现稳定的选股因子。
本节分析讨论了第一部分构建的高频因子的选股效果。2.1~2.3从单因子的角度分别讨论了高频方差、高频偏度以及高频峰度因子的选股能力。2.4简单分析了偏度因子与其他因子的相关性。2.5对于偏度因子进行了正交化处理并分析讨论了正交后因子的选股能力。本节在对于因子选股效果进行回测时使用了2010年1月至2017年3月间的数据,并以月度为周期讨论因子的选股能力。
使用因子值可将市场上所有可交易股票分成10组,并统计不同分组股票在下一个月相对于市场平均收益的超额收益。下图给出了高频方差因子的分组收益特征。本报告中的股票分组按照因子值大小由小到大依次排列。第1组为因子值最小的一组,第10组为因子值最大的一组。
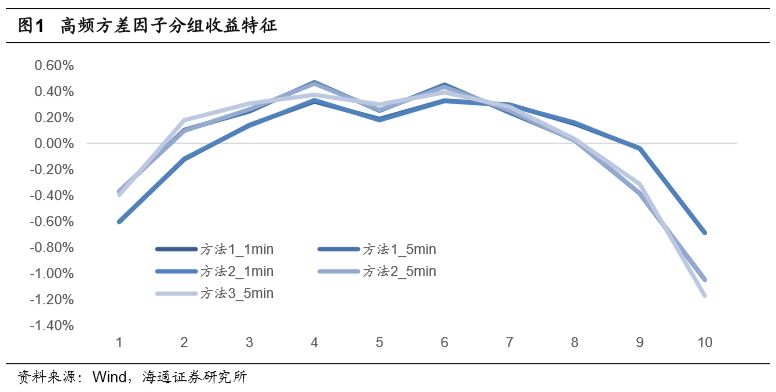
下表详细统计了不同分组股票的平均超额收益情况。
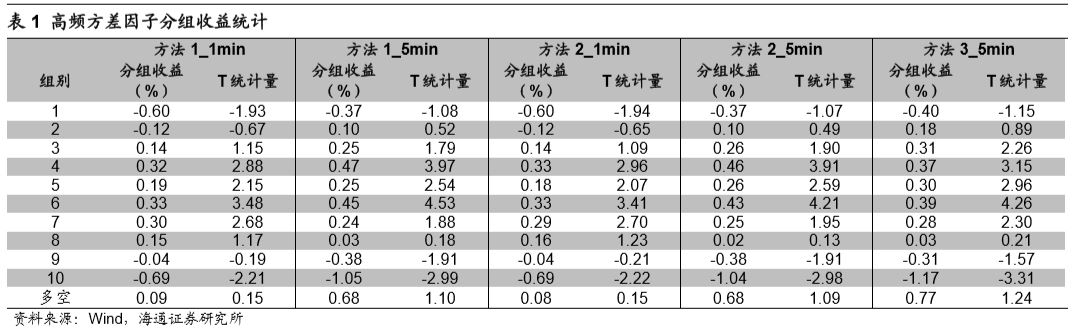
观察上述图表不难发现高频方差因子组间收益单调性较差,因子存在较强的非线性特征。下表统计了不同计算周期以及计算方法下高频方差因子的rankIC、rankICIR、IC胜率。
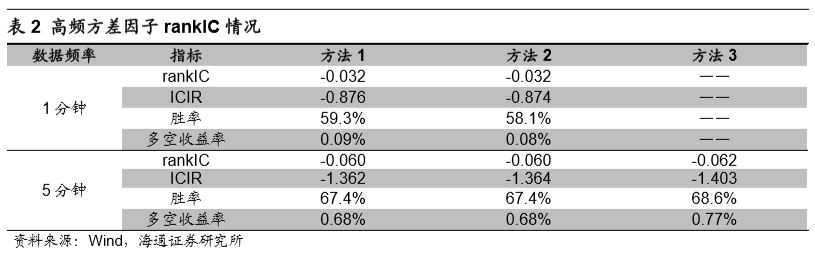
从IC以及ICIR的角度来看,1分钟频率下的高频方差因子并不具有选股能力,5分钟频率下的高频方差因子具有弱选股能力。但是考虑到5分钟高频方差因子组间收益单调性欠佳,本文并不会对于该因子进行进一步分析。
下图展示了不同收益频率以及不同计算方式下高频偏度因子的分组收益特征。
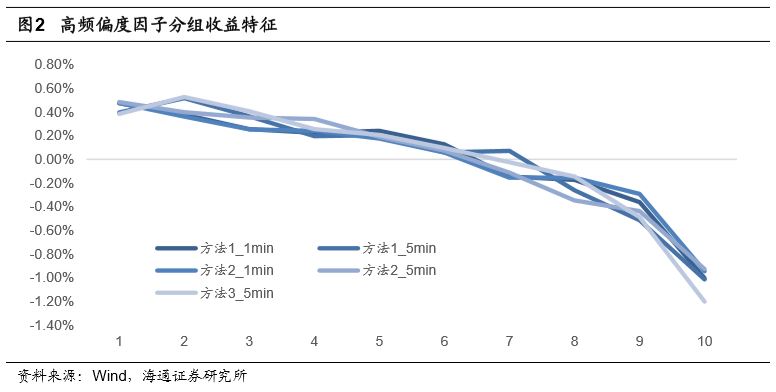
下表详细统计了不同分组股票的平均超额收益情况。
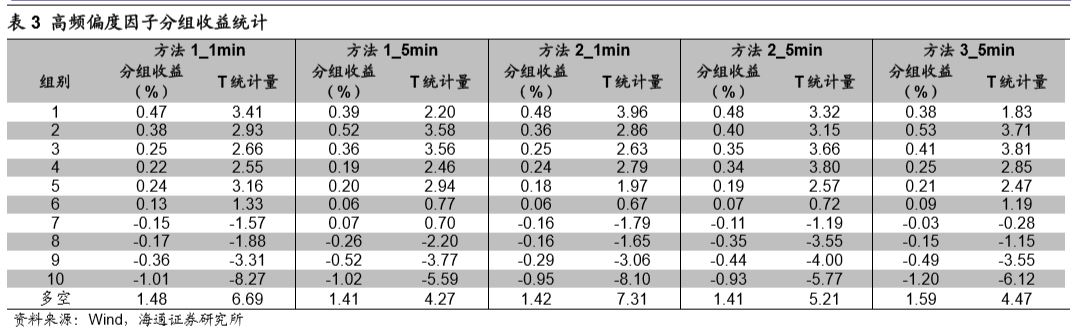
从分组收益可知,高频偏度因子对于股票收益具有较好的区分效果,前期偏度越小的股票未来表现越好。因子月度多空收益约为1.5%,但因子空头收益占比较高。因子多头端平均超额收益约为0.5%,而空头端平均超额收益约为1.0%。下表统计了不同计算周期以及计算方法下高频偏度因子的rankIC、rankICIR、IC胜率。
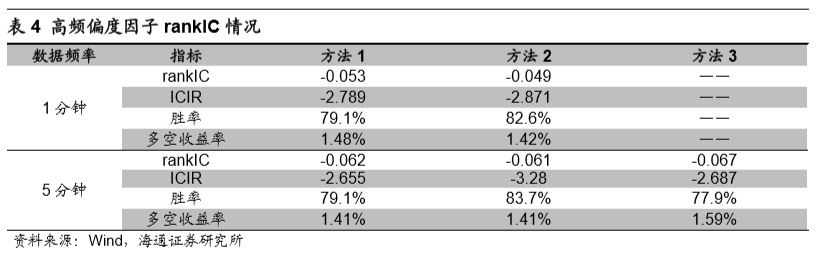
从rankIC以及rankICIR的角度来看,偏度因子同样具有较好的选股能力。不同频率、不同计算方式下因子的rankIC的绝对值基本维持在0.05~0.06左右,ICIR的绝对值普遍高于2.5,因子IC月度胜率接近80%。结合因子分组收益情况,我们认为高频偏度因子具有进一步研究分析的空间。
下图展示了不同收益频率以及不同计算方式下高频峰度因子的分组收益特征。
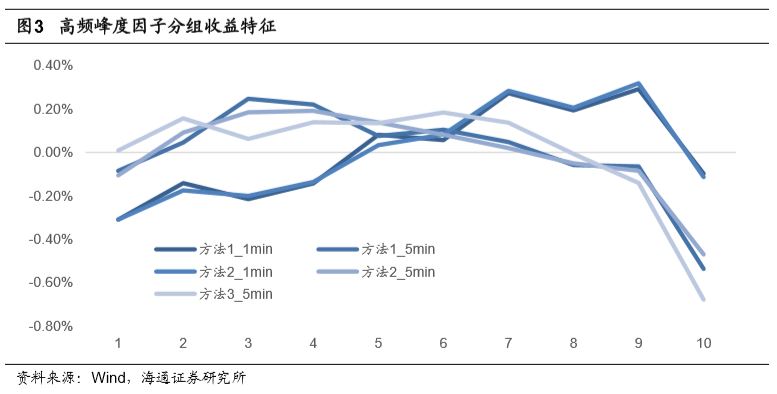
下表详细统计了不同分组股票的平均超额收益情况。
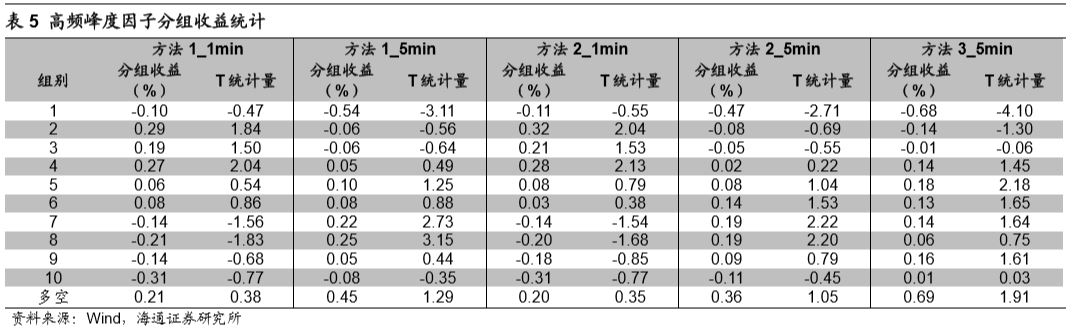
观察上述图表不难发现,不同数据频率下的峰度因子表现存在明显不同。1分钟峰度因子分组收益自第3组开始,随着因子值的上升,分组收益逐渐下降。而5分钟峰度因子,分组收益随着因子值的升高而略有上升。下表统计了不同计算周期以及计算方法下高频峰度因子的rankIC、rankICIR、IC胜率。
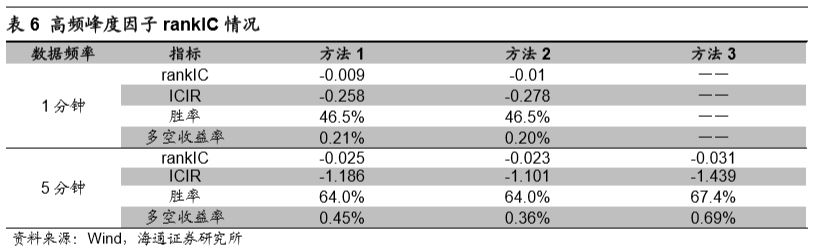
从rankIC以及rankICIR的角度来看,峰度因子选股效果在不同数据频率下同样存在明显差异。简单来说,1分钟峰度因子基本不具有选能力,5分钟峰度因子选股能力较弱。考虑到这种不稳定性,本文暂不对于该因子进行进一步挖掘。
通过上述简单回测可知高频收益偏度因子在不同的收益频率以及不同的计算方法下皆有稳定的选股效果。下图展示了使用高频偏度因子对于股票进行分组后各股票组合的分组特征情况。
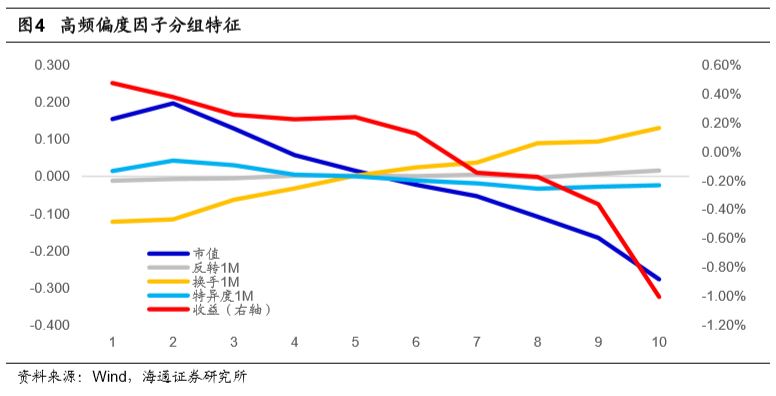
观察上表可知,高频偏度因子多头组合具有大市值、低换手的特征。随着因子值的升高,组别收益逐渐降低。与此同时,组合股票市值逐渐降低,股票前期换手率逐渐升高。因此,高频偏度因子与市值因子负相关,而与换手率因子正相关。此外,不同分组股票对于反转以及特异度的暴露并无明显区分,也即高频偏度因子与反转以及特异度相关性不高。
通过高频方差、高频偏度以及高频峰度因子的初步回测可知,高频偏度因子在不同数据频率以及不同计算方式下皆具有选股能力。考虑到因子与市值以及换手率之间的相关性,本节对于高频偏度因子进行了正交化处理,对于剔除了行业、市值、非线性市值、换手、特异度以及反转影响后的偏度因子进行了回测。(详细处理细节可参考专题报告《选股因子系列研究(十七)——选股因子的正交》。)
下图展示了正交后的高频偏度因子分组收益情况。
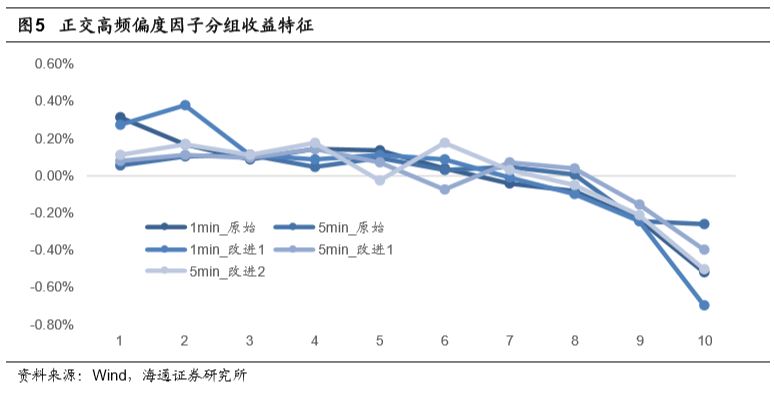
下表统计了不同计算周期以及计算方法下正交高频偏度因子的rankIC、rankICIR、IC胜率。正交后的高频偏度因子选股效果虽受到一定程度的影响,但是因子依旧具有选股能力。1分钟的高频偏度因子IC绝对值下降至0.03附近,但ICIR绝对值依旧在2以上。5分钟高频偏度因子受到的影响较大,IC绝对值下降至0.02附近,ICIR绝对值在1.5~1.7之间。
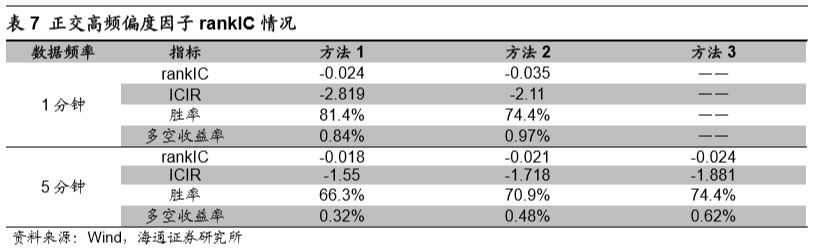
本部分对于不同数据频率、不同计算方法下的高频方差、高频偏度以及高频峰度三个因子进行了回测。从回测结果来看,高频偏度因子具有较为稳健的选股能力。将因子相对于行业、市值、非线性市值、换手、特异度以及反转进行正交后,正交偏度因子依旧具有一定的选股能力。相比而言,正交后的1分钟偏度因子选股能力更强。
##多因子模型回测
由于新因子的研究最终还是要服务于多因子模型,所以本章主要讨论高频偏度因子在加入到多因子模型后对于模型的影响。首先,我们会从回归法的角度讨论因子在加入到模型后是否具有显著的选股效果。其次,我们会从TOP100纯多头组合的角度观察因子在加入到多因子模型后对于模型极端组别表现的影响。
在进行模型对比时,原始模型为使用市值、非线性市值、换手、反转以及特异度因子构建的最大化预期收益月度选股组合。其中,因子集合进行正交化处理。改进模型在原始模型的基础之上考虑加入各数据频率、各计算方法下的高频偏度因子。
本章在进行最大化预期收益多因子组合构建时按照以下规则进行:
1)使用2010年1月至2017年3月间的数据进行回测;
2)每月月末计算因子值,并对因子统一进行截面标准化的处理;
3)分配因子权重时使用历史滚动24月因子表现;
4)在调仓时,组合按照涨停不买、跌停不卖的规则进行;
5)调仓考虑双边千五的交易费用;
6)选股范围剔除ST股、上市不满6个月的股票。
使用2010年1月至2017年2月底之间的数据可分别对于原始模型以及改进模型进行Fama-MacBeth回归检验。由于模型由正交因子组成,所以任意新因子的引入并不会影响原有因子回归系数以及系数的显著性。故而,我们可将注意力集中在新加入因子的回归系数及其T统计量上。
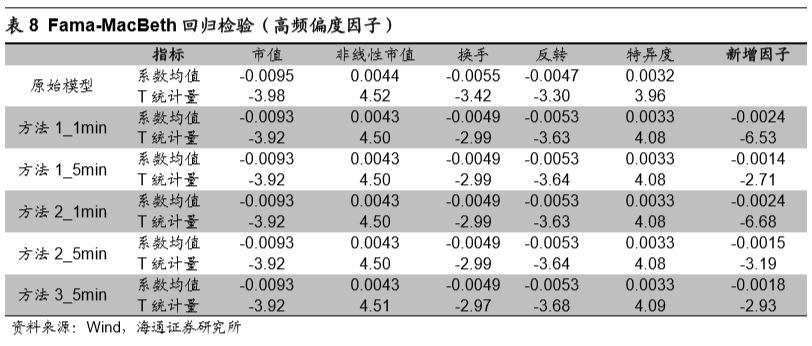
观察新增因子回归系数均值以及T统计量可知,各计算频率以及计算方法下的高频偏度因子在回测时间段中具有显著选股能力。此外,1分钟偏度因子选股效果强于5分钟偏度因子选股效果,这一点在回归系数以及回归系数T统计量绝对值大小上皆有所体现。
基于前文提到的模型构成,可分别使用原始模型以及改进模型在2012年1月至2017年3月底间构建全市场TOP100月度选股组合。在进行选股时剔除上市不满6个月的股票、ST股以及无法交易的股票。下表对比了原始模型TOP100组合以及改进模型TOP100组合的历史表现。
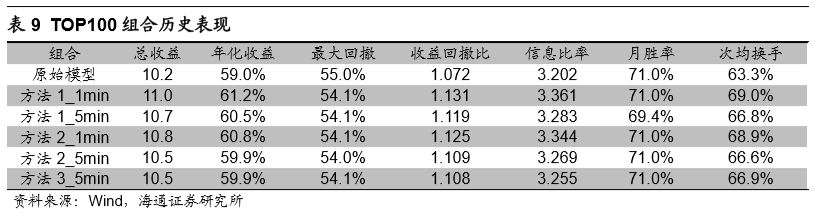
从纯多头组合表现上看,高频因子的引入对于模型极端组合表现的改进较为有限。相比而言,1分钟偏度因子对于组合的提升更为明显。在加入1分钟偏度因子后,TOP100纯多头组合在年化收益、收益回撤比以及信息比率上皆有所提升。在加入5分钟偏度因子后,部分改进模型在年化收益上并未出现改进,仅在收益回撤比以及信息比率上有所提升。这种现象也和前一节中Fama-Macbeth回归的结果相符。
因子对于多因子模型的影响很大程度上取决于因子在模型中所占有的权重,所以本节将展示高频偏度因子在改进模型中所占的权重。
下图展示了加入计算方法1下1分钟偏度因子的多因子模型的因子权重分配情况。从因子权重上看,计算方法1下的1分钟偏度因子在整个多因子模型的权重占比约为10%。
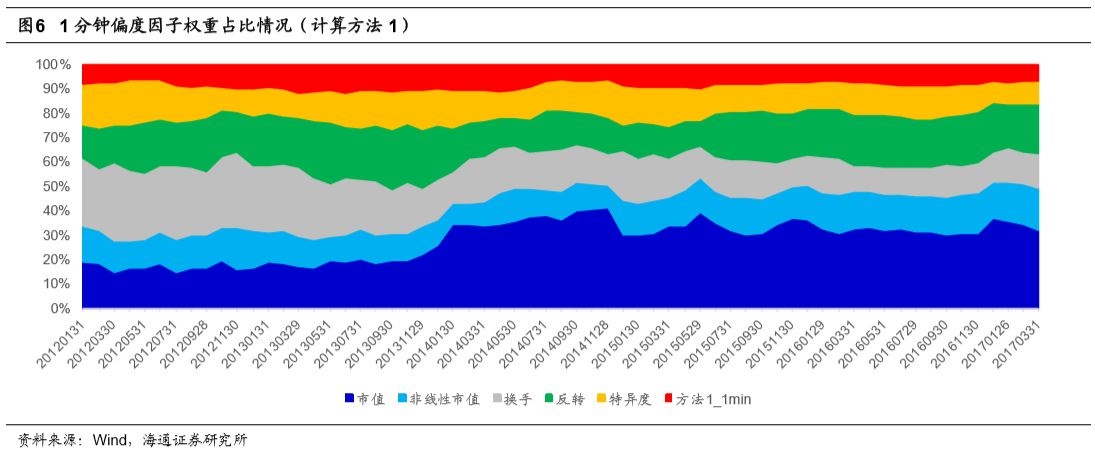
下图展示了加入计算方法1下5分钟偏度因子的多因子模型的因子权重分配情况。从因子权重上看,5分钟偏度因子在整个多因子模型的权重占比低于1分钟偏度因子,权重比例在5%~10%之间波动。
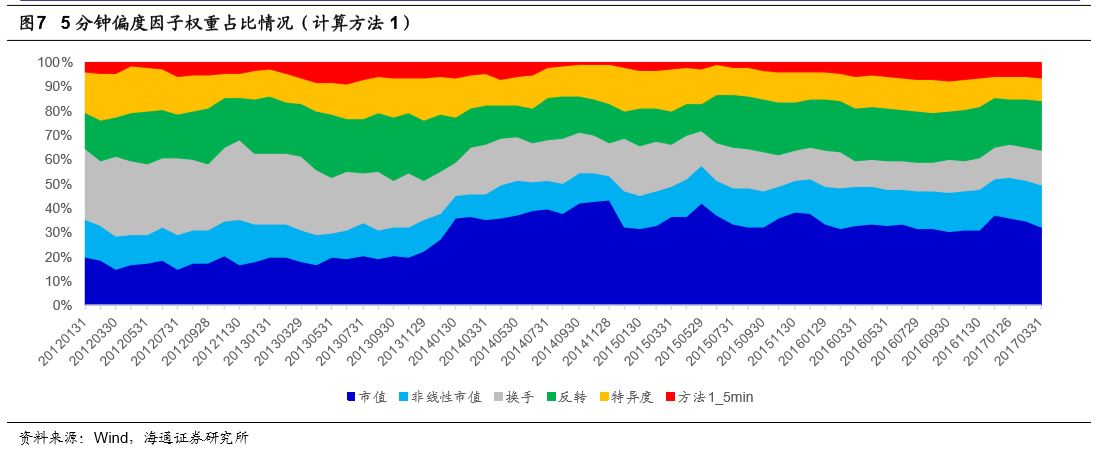
在不同的计算方法下,高频偏度因子的权重占比也并无明显区别。下图展示了方法2下1分钟偏度因子的权重占比。在回测区间中,1分钟偏度因子权重占比也基本在10%左右波动。
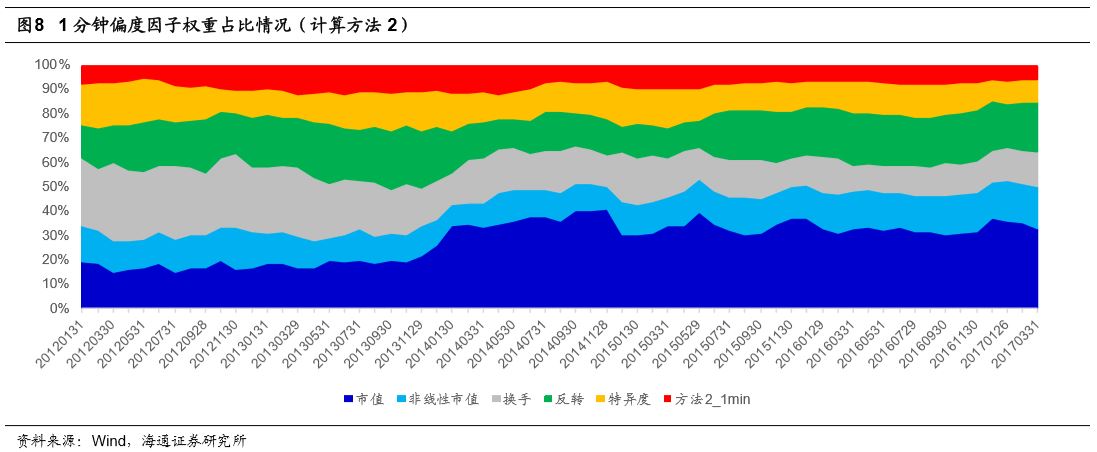
下图展示了计算方法2下5分钟偏度因子的权重占比。5分钟偏度因子的权重比率基本在5%至10%之间波动。
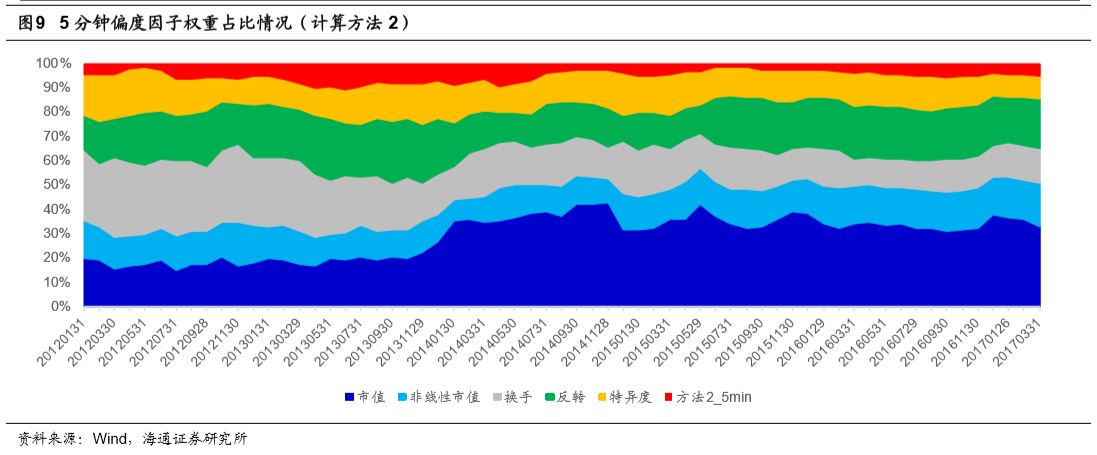
在方法3下,5分钟偏度因子的权重占比依旧没有明显变化,依旧处于5%~10%的范围内。
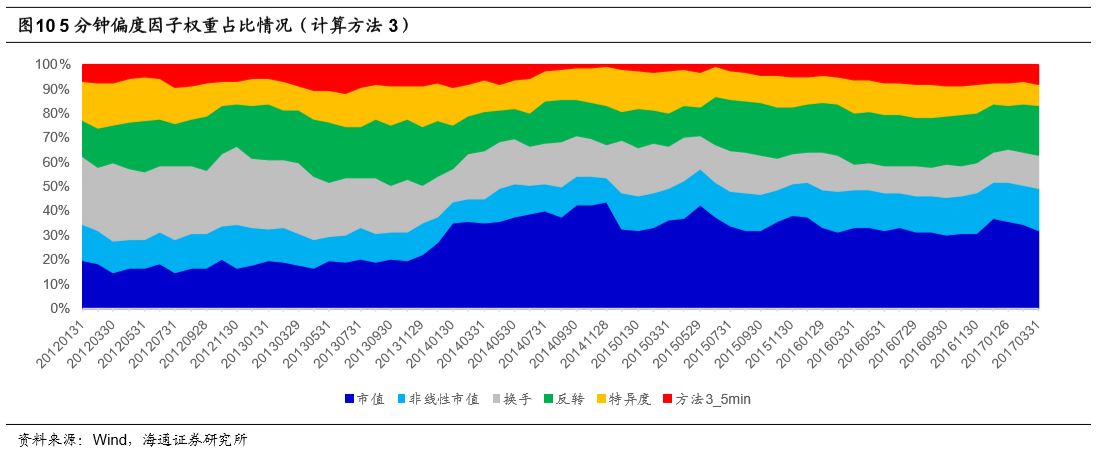
本部分将高频偏度因子放入到了多因子模型的框架中,从Fama-MacBeth回归、TOP100纯多头组合以及因子权重占比三个方面进行了分析。综合来看,高频偏度因子在纳入到多因子模型后能够为模型贡献显著的额外选股能力。但是对于极端组别来说,高频偏度因子能够带来的改进较为有限。从因子权重的角度来看,1分钟偏度权重占比约为10%,5分钟偏度权重占比在5%~10%之间。
本文基于股票高频价格数据,从收益方差、收益偏度以及收益峰度三个角度对于股票高频收益的分布特征进行了刻画。通过回测,我们发现高频偏度因子在不同的数据频率以及不同的计算方法下都有着较为稳健的选股能力。在对于高频偏度因子进行正交处理后,因子依旧保留有一定的选股能力,所以我们认为该因子可以被纳入到多因子模型中进行进一步的分析讨论。
从Fama-MacBeth回归的结果来看,高频偏度因子能够为模型提供显著的额外选股能力。但是对于模型的极端组合来说,因子的引入对于组合的年化收益以及信息比率的提升较为有限。相比而言,1分钟偏度因子对于模型的提升效果更好。此外,从因子权重来看,1分钟偏度因子权重占比约为10%,5分钟偏度因子权重占比在5%~10%之间。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
