流动性市场的大量参与者，他们在经营时会基于不同的投资期限，这便产生了很多市场噪音。 因此，市场的信噪比较低。 尝试整数型时间序列差分能令情况恶化，其会消除残余记忆，并将报价转换为以平稳性为特征的序列。
价格序列有记忆性，因为每个数值都建立在具有悠久历史的价位之上。 时间序列变换，例如增量对数，会裁剪记忆，因为它们是基于有限的窗口长度来创建的。 当转换平稳地消除市场记忆时，统计学家使用复杂的数学方法来提取残余的记忆。 这就是为什么许多相关的经典统计方法会导致虚假的结果。
长期依赖（LRD），也称为长期记忆或长期持续，是一种分析金融时间序列时可能出现的现象。 它可表示为两个价格之间的统计依赖性的衰减率随时间间隔（或它们之间的距离）的增加而增加。 当依赖性衰减慢于指数衰减时，这种现象则被认为具有长期依赖性。 长期依赖通常也与自相似过程相关。 有关 LRD（长期依赖）的详情，请参阅维基百科文章。
价格图表的一个共同特征是非平稳性：它们有很长的价位历史，随时间的推移平均价格会改变。 为了进行统计分析，研究人员需要处理价格增量（或增量的对数），盈利能力或波动性的变化。 这些变换可从价格序列中消除记忆，令时间序列更加平稳。 虽然平稳性是统计结论的必要属性，但并非总需要消除整个记忆，因为记忆是预测模型的基础属性。 例如，均衡（平稳）模型必须包含一些记忆，以便能够评估价格偏离其预期价值的程度。
问题在于价格增量是固定的，但不包含过去的记忆，而价格序列包含全部数量的可用记忆，但它是非稳定性的。 问题出现了：如何差分时间序列令其平稳，同时最大程度地保留可能记忆。 因此，我们理应概括价格增量的概念，以便研究平稳性系列，其中并非所有记忆都被消除。 在这种情况下，比之其他可用方法，价格增量不是价格变换的最优解。
为此，将引入分数型差分的概念。 两个极端之间存在广泛的可能性：单一和零差分。 在一侧来看，它们是完全不同的价格。 从另一侧来看，价格没有任何差别。
分数型差分的应用范围足够广泛。 例如，差分序列通常作为机器学习算法的输入。 问题是，必须在机器学习模型可识别的前提下，显示相应历史阶段的新数据。 在非平稳序列的情况下，由于模型可能地错误操作，新数据也许位于已知数值范围之外。
在各种科技文献中论述的几乎所有用于分析和预测金融时间序列的方法，都提出了整数型差分的概念。
在这方面会出现以下问题：
应用于时间序列分析和预测的分数型差分概念至少可以追溯到霍金斯（Hosking）。 在他文章中，ARIMA 过程家族是广义的，允许差分度拥有分数部分。 这是有道理的，因为分数型差分过程体现出长期持久性或抗持久性，因此比之标准ARIMA 提高了预测能力。 该模型被称为 ARFIMA（自回归分数积分移动平均值）或 FARIMA。 之后，其他作者在主要与加速计算方法相关的文献中有时会提到分数型差分。
这种模型可用于长期记忆时间序列的建模，即，自长期平均值的偏差比指数衰减更慢的情况下。
我们来研究回漂运算符（或滞后算子） B ，应用于实数值矩阵{Xt}，其中 B^kXt = Xt-k，对于任意整数 k ≥ 0。 例如，(1 − B)^2 = 1 − 2B + B^2，其中 B^2Xt = Xt−2，由此，(1 − B)^2Xt = Xt − 2Xt−1 + Xt−2。
注意 (x + y)^n =
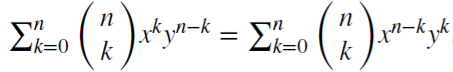针对每个正整数
n。 对于实数值 d，
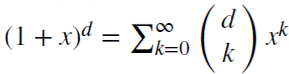则是一个二项式序列。
在分数模型中，
d 可以是具有以下二项式序列正式扩展的实数值：
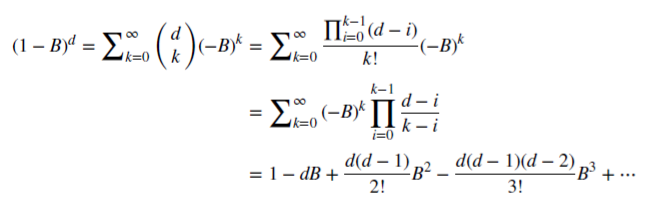
我们来看看有理非负 d 如何能够保留记忆。 该算术序列由标量乘积组成：
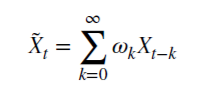
含有权重 𝜔
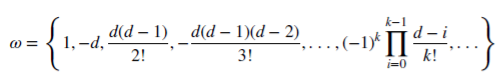
合数值 X
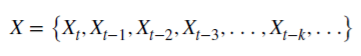
当 d 为正整数时，
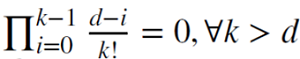，在这种情况下，记忆被裁剪。
例如，d = 1 用于计算增量，
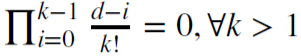且 𝜔
= {1,−1, 0, 0,…}。
分数型差分通常应用于时间序列的整个顺序。 在这种情况下，计算的复杂性更高，而变换序列的偏移则是负数。 Marcos Lopez De Prado 在其 金融机器学习的进展 一书中提出了一种固定宽度窗口的方法，其中当模块 (|𝜔k|) 小于指定阈值 (𝜏) 时，系数顺序会被丢弃。 与传统的扩展窗口方法相比，该过程具有以下优点：对于任何原始序列的顺序它允许具有相等的权重，降低计算复杂度，并消除回漂。 这种转换可以保存有关价位和噪音的记忆。 由于存在记忆、不对称和过度峰度，这种变换不是正态（高斯）分布，然而它可以平稳的。
我们创建一个脚本，令您可以直观地从时间序列的分数型差分中评估获得的效果。 我们会创建两个函数：一个用于获得权重 ω，另一个用于计算序列的新值：
//+------------------------------------------------------------------+ void get_weight_ffd(double d, double thres, int lim, double &w[]) { ArrayResize(w,1); ArrayInitialize(w,1.0); ArraySetAsSeries(w,true); int k = 1; int ctr = 0; double w_ = 0; while (ctr != lim - 1) { w_ = -w[ctr] / k * (d - k + 1); if (MathAbs(w_) < thres) break; ArrayResize(w,ArraySize(w)+1); w[ctr+1] = w_; k += 1; ctr += 1; } } //+------------------------------------------------------------------+ void frac_diff_ffd(double &x[], double d, double thres, double &output[]) { double w[]; get_weight_ffd(d, thres, ArraySize(x), w); int width = ArraySize(w) - 1; ArrayResize(output, width); ArrayInitialize(output,0.0); ArraySetAsSeries(output,true); ArraySetAsSeries(x,true); ArraySetAsSeries(w,true); int o = 0; for(int i=width;i<ArraySize(x);i++) { ArrayResize(output,ArraySize(output)+1); for(int l=0;l<ArraySize(w);l++) output[o] += w[l]*x[i-width+l]; o++; } ArrayResize(output,ArraySize(output)-width); }
我们显示一个动画图表，该图表根据参数 0<d<1: 而变化
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { for(double i=0.05; i<1.0; plotFFD(i+=0.05,1e-5)) } //+------------------------------------------------------------------+ void plotFFD(double fd, double thresh) { double prarr[], out[]; CopyClose(_Symbol, 0, 0, hist, prarr); for(int i=0; i < ArraySize(prarr); i++) prarr[i] = log(prarr[i]); frac_diff_ffd(prarr, fd, thresh, out); GraphPlot(out,1); Sleep(500); }
此为结果:
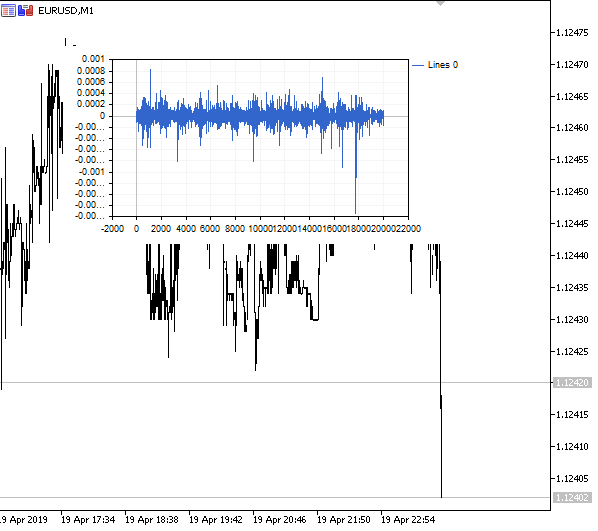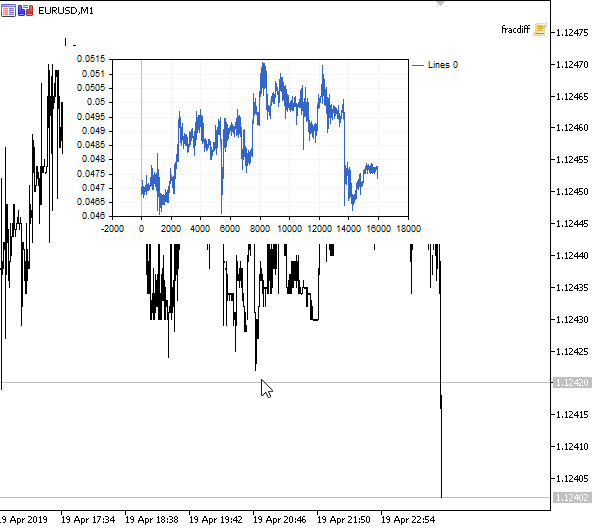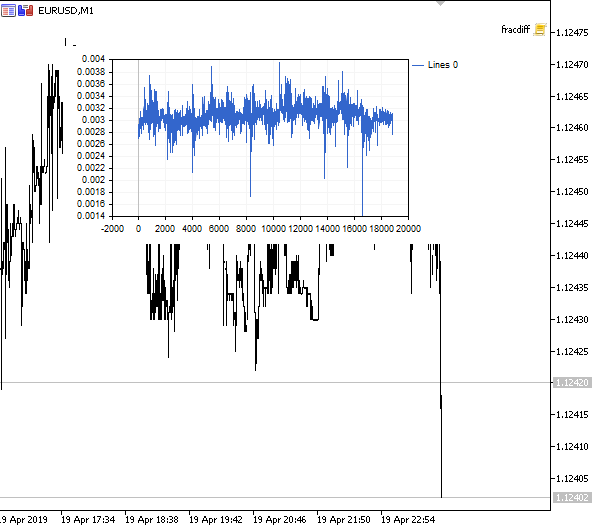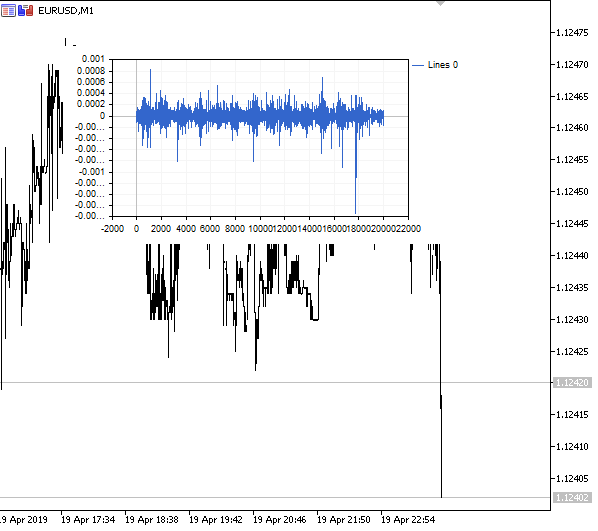
图例 1. 分数型差分 0<d<1
正如预期的那样，随着差分度 d 的增加，图表变得更加平稳，同时逐渐失去以往价位的“记忆”。 序列的权重（按价格值计算的标量乘积的函数）在整个序列期间保持不变，不需要重新计算。
为了便于在智能交易系统中使用，我们创建一个指标，应能够指定各种参数：差分度，删除过度权重的阈值大小，和显示历史的深度。 我不会在这里发布完整的指标代码，您可以在源文件中查看它。
我仅指出权重计算函数是相同的。 以下函数用于计算指标缓冲区数值：
frac_diff_ffd(weights, price, ind_buffer, hist_display, prev_calculated !=0);
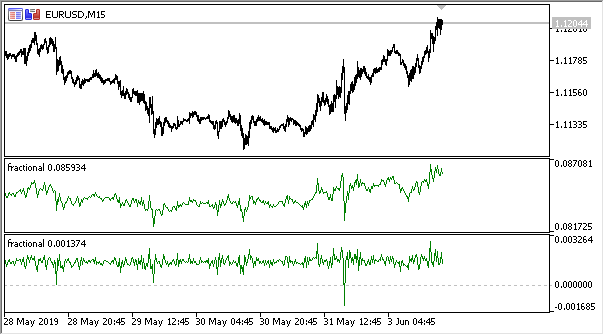
图例 2. 幂指数为 0.3 和 0.9 的分数型差分
现在我们拥有了一个指标，可以非常准确地指示时间序列中动态变化的信息量。 当差分度增加时，信息丢失，序列变得更加平稳。 不过，只有价位数据丢失。 也许剩下的是周期性循环，它将成为预测的参考点。 因此，我们正在接近信息论方法，即信息熵，这将有助于评估数据量。
信息熵是与信息论相关的概念，它示意事件中包含的信息量。 通常，事件越具体或确定，它所包含的信息越少。 更具体地说，信息与不确定性的增加有关。 这个概念是由 Claude Shannon 引入的。
随机值的熵可以通过引入随机 X 值的分布概念来判定，该值取有限数量的值：
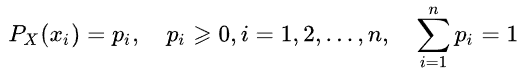
然后，事件（或时间序列）的具体信息定义如下：
熵值评估可以如下书写：
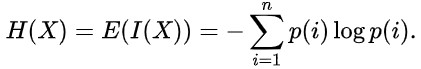
信息量和熵的测量单位取决于对数基数。 例如，这可以是 bits，nat，trits 或 hartleys。
我们不会详细阐述 Shannon 的熵理论。 然而，应当注意的是，这种方法不适合评估短期和有噪声的时间序列。 因此，Steve Pincus 和 Rudolf Kalman 提出了一种与金融时间序列相关的称为 “ ApEn”（近似熵）的方法。 该方法在 “不规则，波动，风险和金融市场时间序列” 一文中有详细论述。
在该文中，他们研究了两种形式的价格自恒定值偏离（波动率的描述），它们本质上是不同的：
这两种形式完全不同，因此这种分离是必要的：标准偏差仍然是测量距中心偏差的优异估算方法，而 ApEn 提供了针对不规则性的估计。 甚或，变异度不是很关键，而不规则性和不可预测性确实是一个问题。
此为一个包含两个时间序列的简单示例：
统计时刻，例如均值和方差，不会显示两个时间序列之间的差值。 与此同时，第一个序列是完全正规的。 这意味着知道以前的值，您可以随时预测下一个值。 第二个序列绝对是随机的，因此任何预测尝试都将失败。
Joshua Richman 和 Randall Moorman 在他们的文章“利用近似熵和样本熵的生理时间分析来进行分析”中抨击了 ApEn 方法。 代之，他们建议改进 “SampEn” 方法。 特别是，他们指责熵值对样本长度的依赖性，以及相关时间序列的数值不一致性差别。 而且，新提供的计算方法没有那么复杂。 我们将运用此方法，且将描述其应用程序的功能。
SampEn 是 ApEn 方法的一个改编版本。 它用于评估信号的复杂性（不规则性）（时间序列）。 对于指定的 m 点的大小，计算 r 公差和 N 的值，SampEn 为概率的对数，如果两个并发点数系列的长度为 m，距离为 r，那么两个并发点数序列长度 m + 1的距离也是 r。
假设我们有一个时间序列数据集合，长度为
，它们之间有一个恒定的时间间隔。
我们定义长度为 m 的矢量模板，如此
和距离函数
（i≠j）乘以
Chebyshev，此为这些矢量组件之间差值的最大模数（但这也可以是另一个距离函数）。 那么，SampEn 将定义如下：
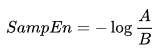
其中:
从上面可以清楚地看出，A 总是 <= B，因此 SampEn 始终为零或正值。 数值越低，数据集合中的自相似性越大，噪音越低。
主要使用以下值：m= 2 且 r= 0.2 * std，其中 std 是应对非常大的数据集合而采用的标准偏差。
我在以下代码中找到了所提议方法的快速实现，并以 MQL5 重新编写了它：
double sample_entropy(double &data[], int m, double r, int N, double sd) { int Cm = 0, Cm1 = 0; double err = 0.0, sum = 0.0; err = sd * r; for (int i = 0; i < N - (m + 1) + 1; i++) { for (int j = i + 1; j < N - (m + 1) + 1; j++) { bool eq = true; //m - length series for (int k = 0; k < m; k++) { if (MathAbs(data[i+k] - data[j+k]) > err) { eq = false; break; } } if (eq) Cm++; //m+1 - length series int k = m; if (eq && MathAbs(data[i+k] - data[j+k]) <= err) Cm1++; } } if (Cm > 0 && Cm1 > 0) return log((double)Cm / (double)Cm1); else return 0.0; }
此外，我建议附带选项，在需要获得两个序列（两个输入向量）的估算熵值时，计算交叉样本熵（cross-SampEn）。 不过，它也可以用来计算样本熵：
// Calculate the cross-sample entropy of 2 signals // u : signal 1 // v : signal 2 // m : length of the patterns that compared to each other // r : tolerance // return the cross-sample entropy value double cross_SampEn(double &u[], double &v[], int m, double r) { double B = 0.0; double A = 0.0; if (ArraySize(u) != ArraySize(v)) Print("Error : lenght of u different than lenght of v"); int N = ArraySize(u); for(int i=0;i<(N-m);i++) { for(int j=0;j<(N-m);j++) { double ins[]; ArrayResize(ins, m); double ins2[]; ArrayResize(ins2, m); ArrayCopy(ins, u, 0, i, m); ArrayCopy(ins2, v, 0, j, m); B += cross_match(ins, ins2, m, r) / (N - m); ArrayResize(ins, m+1); ArrayResize(ins2, m+1); ArrayCopy(ins, u, 0, i, m + 1); ArrayCopy(ins2, v, 0, j, m +1); A += cross_match(ins, ins2, m + 1, r) / (N - m); } } B /= N - m; A /= N - m; return -log(A / B); } // calculation of the matching number // it use in the cross-sample entropy calculation double cross_match(double &signal1[], double &signal2[], int m, double r) { // return 0 if not match and 1 if match double darr[]; for(int i=0; i<m; i++) { double ins[1]; ins[0] = MathAbs(signal1[i] - signal2[i]); ArrayInsert(darr, ins, 0, 0, 1); } if(darr[ArrayMaximum(darr)] <= r) return 1.0; else return 0.0; }
第一种计算方法就已足够了，因此会进一步使用。
如果价格序列增量的数值目前正在增加，那么下一时刻持续增长的概率是多少？ 现在我们来研究持久性。 持久性的测量可以提供很大的助力。 在本节中，我们将研究 SampEn 方法应用程序来评估滑动窗口中增量的持久性。 该评估方法在上述文章“ 不规则，波动，风险和金融市场时间序列”中提出。
根据分数型布朗运动理论，我们已经有了一个差分系列（这是“分数型差分”项的出处）。 定义粗粒度二进制增量序列
BinInci:= +1, 如果 di+1 – di > 0, –1. 简单地说，将增量在范围 +1，-1 之间二值化。 因此，我们直接估计增量行为的四种可能变体的分布：
估算的独立性和方法的统计功效与以下特征相关：几乎所有过程对于 Binlnci 序列都具有极小的 SampEn 误差。 更重要的事实是，估算并不意味着，且并不要求数据对应于马尔可夫链，并且它不需要事先知道除了平稳性之外的任何其他特征。 如果数据满足一阶马尔可夫属性，则 SampEn(1) = SampEn(2)，这样便可得出其他结论。
分数型布朗运动的模型可以追溯到 Benoit Mandelbrot，他为表现出长期依赖或“记忆”和“重尾”的现象进行了建模。 这也导致出现了新的统计应用，例如 Hurst 指数和 R/S 分析。 正如我们所知的那样，价格增长有时表现出长期依赖性和重尾。
因此，我们可以直接评估时间序列的持久性：最低的 SampEn 数值将对应于最大的持久性数值，反之亦然。
我们重新编写指标，并添加在持久性评估模式下运行的可能性。 由于熵估算适用于离散值，因此我们需要将增量值标准化，精度最高为 2 位。
完整实现可在附加的 “fractional entropy” 指标中找到。 指标设置如下所述：
input bool entropy_eval = true; // show entropy or increment values input double diff_degree = 0.3; // the degree of time series differentiation input double treshhold = 1e-5; // threshold to cut off excess weight (the default value can be used) input int hist_display = 5000; // depth of the displayed history input int entropy_window = 50; // sliding window for the process entropy evaluation
下图示意了两种模式下的指标（上部显示熵，下部显示标准化增量）：
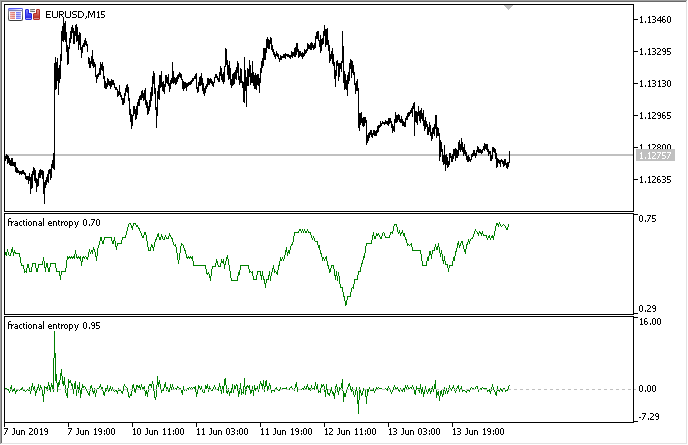
图例 3. 滑动窗口 50（上面）的熵值，和 0.8 度的分数型差分
可以看出，这两个估算值并不相关，这是机器学习模型（没有多重共线性）的一个好兆头，将在下一节中讨论。
因此，我们已拥有一个适当的差分时间序列，可用于生成交易信号。 上面提到过过，时间序列更加平稳，对于机器学习模型更加方便。 我们还有序列持久性评估。 现在我们需要选择最佳的机器学习算法。 由于 EA 必须在其自身内进行优化，因此需要学习速度，该速度必须非常快，并且必须具有最小的延迟。 出于这些原因，我选择了逻辑回归。
运用逻辑回归来预测事件的概率，是基于一组变量 x1，x2，x3 ... xN， 的数值，这些变量也称为预测因子或回归因子。 在我们的例子中，变量是指标值。 还必须引入依赖变量 y，其通常等于 0 或 1。 因此，它可以作为买入或卖出的信号。 基于回归因子的值，计算依赖变量属于特定类的概率。
假设 y = 1 出现的概率等于:
其中
是自变量值
1，x1，x2 ... xN 的向量和回归系数，f(z) 是逻辑函数，或 sigmoid ：
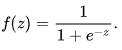结果则为，给定
x 的 y 分布函数可以写成如下：
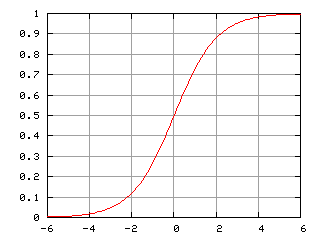
图例 4. 逻辑曲线（sigmoid）。 来源: 维基百科。
我们不会详述逻辑回归算法，因为它是众所周知的。 我们利用 Alglib 函数库中现成的 CLogitModel 类。
我们创建一个单独的类 CAuto_optimizer，它将代表简单虚拟测试器和 logit 回归的组合：
//+------------------------------------------------------------------+ //|Auto optimizer class | //+------------------------------------------------------------------+ class CAuto_optimizer { private: // Logit regression model ||||||||||||||| CMatrixDouble LRPM; CLogitModel Lmodel; CLogitModelShell Lshell; CMNLReport Lrep; int Linfo; double Lout[]; //|||||||||||||||||||||||||||||||||||||||| int number_of_samples, relearn_timout, relearnCounter; virtual void virtual_optimizer(); double lVector[][2]; int hnd, hnd1; public: CAuto_optimizer(int number_of_sampleS, int relearn_timeouT, double diff_degree, int entropy_window) { this.number_of_samples = number_of_sampleS; this.relearn_timout = relearn_timeouT; relearnCounter = 0; LRPM.Resize(this.number_of_samples, 5); hnd = iCustom(NULL, 0, "fractional entropy", false, diff_degree, 1e-05, number_of_sampleS, entropy_window); hnd1 = iCustom(NULL, 0, "fractional entropy", true, diff_degree, 1e-05, number_of_sampleS, entropy_window); } ~CAuto_optimizer() {}; double getTradeSignal(); };
在 //Logit 回归模型// 部分中创建以下内容：x 和 y 值的矩阵，logit 模型 Lmodel 及其辅助类。 训练模型后，Lout[] 数组将接收属于任意类的信号概率，0:1。
构造函数接收学习窗口 number_of_samples 的大小，此后，模型将被重新优化 relearn_timout，针对 diff_degree 指标的分数型差分度，以及熵计算窗口 entropy_window。
我们详细考察 virtual_optimizer() 方法：
//+------------------------------------------------------------------+ //|Virtual tester | //+------------------------------------------------------------------+ CAuto_optimizer::virtual_optimizer(void) { double indarr[], indarr2[]; CopyBuffer(hnd, 0, 1, this.number_of_samples, indarr); CopyBuffer(hnd1, 0, 1, this.number_of_samples, indarr2); ArraySetAsSeries(indarr, true); ArraySetAsSeries(indarr2, true); for(int s=this.number_of_samples-1;s>=0;s--) { LRPM[s].Set(0, indarr[s]); LRPM[s].Set(1, indarr2[s]); LRPM[s].Set(2, s); if(iClose(NULL, 0, s) > iClose(NULL, 0, s+1)) { LRPM[s].Set(3, 0.0); LRPM[s].Set(4, 1.0); } else { LRPM[s].Set(3, 1.0); LRPM[s].Set(4, 0.0); } } CLogit::MNLTrainH(LRPM, LRPM.Size(), 3, 2, Linfo, Lmodel, Lrep); double profit[], out[], prof[1]; ArrayResize(profit,1); ArraySetAsSeries(profit, true); profit[0] = 0.0; int pos = 0, openpr = 0; for(int s=this.number_of_samples-1;s>=0;s--) { double in[3]; in[0] = indarr[s]; in[1] = indarr2[s]; in[2] = s; CLogit::MNLProcess(Lmodel, in, out); if(out[0] > 0.5 && !pos) {pos = 1; openpr = s;}; if(out[0] < 0.5 && !pos) {pos = -1; openpr = s;}; if(out[0] > 0.5 && pos == 1) continue; if(out[0] < 0.5 && pos == -1) continue; if(out[0] > 0.5 && pos == -1) { prof[0] = profit[0] + (iClose(NULL, 0, openpr) - iClose(NULL, 0, s)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } if(out[0] < 0.5 && pos == 1) { prof[0] = profit[0] + (iClose(NULL, 0, s) - iClose(NULL, 0, openpr)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } } GraphPlot(profit); }
该方法显然非常简单，因此很快速。 在一个循环中以指标值 + 线性趋势值（已添加）填充 LRPM 矩阵的第一列。 在接下来的循环中，将当前收盘价与前收盘价进行比较，以澄清交易的可能性：买入或卖出。 如果当前值大于前值，那么就会有一个买入信号。 否则是一个卖出信号。 相应地，以下数据列会填充数值 0 和 1。
所以，这是一个非常简单的测试器，其目的不是为了选择最佳信号，而是在每根柱线上简单地读取它们。 可以通过方法重载来改进测试器，但这超出了本文的范畴。
之后使用 MNLTrain() 方法训练 logit 回归，该方法接受矩阵、其大小、变量数 x（每个案例只传递一个变量），Lmodel 类对象为保存已训练的模型和辅助类。
训练后，模型将在优化器窗口中进行测试，并显示为余额图。 这个视觉效果，能够显示模型如何依据学习样本进行训练。 但是从算法的角度来看，并没有进行性能分析。
从以下方法调用虚拟优化器：
//+------------------------------------------------------------------+ //|Get trade signal | //+------------------------------------------------------------------+ double CAuto_optimizer::getTradeSignal() { if(this.relearnCounter==0) this.virtual_optimizer(); relearnCounter++; if(this.relearnCounter>=this.relearn_timout) this.relearnCounter=0; double in[], in1[]; CopyBuffer(hnd, 0, 0, 1, in); CopyBuffer(hnd1, 0, 0, 1, in1); double inn[3]; inn[0] = in[0]; inn[1] = in1[0]; inn[2] = relearnCounter + this.number_of_samples - 1; CLogit::MNLProcess(Lmodel, inn, Lout); return Lout[0]; }
它会检查自上次训练以来已经历过的柱线数量。 如果该值超过指定的阈值，则应重新训练模型。 之后，按时间单位，自上次训练过后的最后一个指标值将被复制。 这是利用 MNLProcess() 方法输入到模型中的，该方法返回的结果表示该值是否属于类 0:1，即交易信号。
现在我们需要将函数库连接到智能交易系统，并添加信号处理程序：
#include <MT4Orders.mqh> #include <Math\Stat\Math.mqh> #include <Trade\AccountInfo.mqh> #include <Auto optimizer.mqh> input int History_depth = 1000; input double FracDiff = 0.5; input int Entropy_window = 50; input int Recalc_period = 100; sinput double MaximumRisk=0.01; sinput double CustomLot=0; input int Stop_loss = 500; //Stop loss, positions protection input int BreakEven = 300; //Break even sinput int OrderMagic=666; static datetime last_time=0; CAuto_optimizer *optimizer = new CAuto_optimizer(History_depth, Recalc_period, FracDiff, Entropy_window); double sig1;
智能交易系统的设置很简单，包括窗口大小 History_depth，即自动优化器的训练示例数量。 差分度 FracDiff 和接收的柱线数量 Recalc_period，之后将重新训练模型。 此外，还添加了 Entropy_window 设置以便调整熵计算窗口。
最后一个函数从训练模型接收信号，并执行交易操作：
void placeOrders(){ if(countOrders(0)!=0 || countOrders(1)!=0) { for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true) { if(OrderType()==0 && sig1 < 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; if(OrderType()==1 && sig1 > 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } if(countOrders(0)!=0 || countOrders(1)!=0) return; if(sig1 > 0.5 && (OrderSend(Symbol(),OP_BUY,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN)>0)) { return; } if(sig1 < 0.5 && (OrderSend(Symbol(),OP_SELL,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN)>0)) {} }
如果买入的概率大于 0.5，则此为买入信号，和/或空头持仓的平仓信号。 反之亦然。
我们来看看最有趣的部分，i8.e。 测试。
智能交易系统利用指定的超参数运行，没有遗传优化，即几乎是随机，在 15 分钟的时间帧内以开盘价格在 EURUSD 货币对上运行。
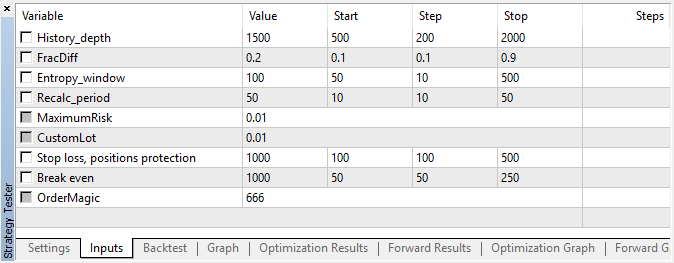
图例 5. 已测试智能交易系统的设置
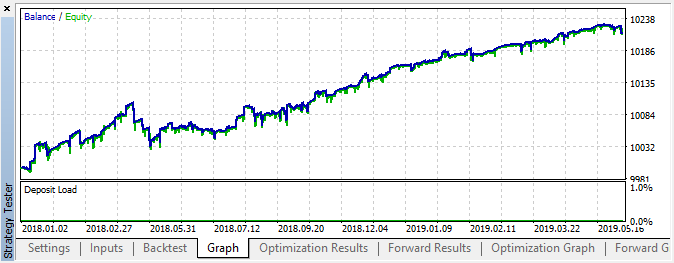
图例 6. 按照指定设置进行测试的结果
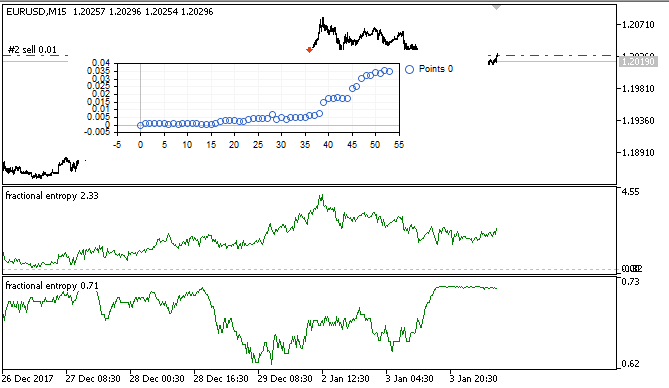
图例 7. 依据训练样本的虚拟测试器结果
在此间隔内，显示稳定增长，这意味着该方法可用于进一步分析。
结果就是，我们尝试了在一篇文章中实现三个目标，包括以下内容：
本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
