from jqdata import*
import statsmodels.api as sm
import datetime
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

#前置条件
current_date = datetime.date(2018,12,10)
stock_list = get_index_stocks('000906.XSHG',date = current_date)
trade_days = list(get_all_trade_days())

#准备数据
market_query = query(indicator.roe,
                    valuation.market_cap,
                    valuation.pe_ratio).filter(
                valuation.code.in_(stock_list))
MKT_data = get_fundamentals(market_query,date = current_date)
price_data = get_price(stock_list,current_date,current_date,'1d',['close'])['close'].T
MKT_data['price'] = array(price_data)

#无处理回归结果
x = MKT_data[['roe','market_cap','pe_ratio']]
y = MKT_data['price']
model = sm.OLS(y,x)
result = model.fit()
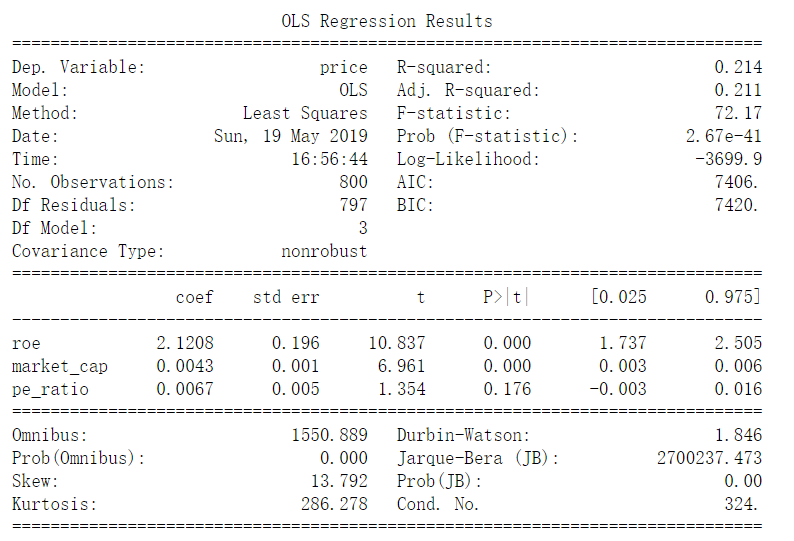
print(result.summary())

#寻找核向量，最小化距离极值处理方法
def cal_sumdis(vector,mat):
    dis_mat = float(((mat - vector) ** 2).sum(axis = 1).sum())
    return dis_mat
def min_dis_vector(mat):
    array_mat = array(mat)
    min_vector = array_mat[0]
    min_dis = cal_sumdis(min_vector,mat)
    for vector in array(mat)[1:]:
        if cal_sumdis(vector,mat) < min_dis:
            min_dis = cal_sumdis(vector,mat)
            min_vector = vector
        else:
            pass
    return min_vector

#按照上述方法寻找核向量
min_dis_vec = min_dis_vector(MKT_data)

#核向量和其他点的距离
dis_spread = ((MKT_data - min_dis_vec) ** 2).sum(axis = 1)

#观察最小距离分布
dis_spread.plot(title = '核向量方法数据分布描述')

#观察市值的数值分布
a = MKT_data['market_cap'].plot()
b = MKT_data['pe_ratio'].plot()
c = MKT_data['roe'].plot()

#修改函数
def new_cal_sumdis(vector,mat):
    dis_mat = (mat - vector) ** 2
    return dis_mat / (dis_mat.mean(axis = 0) / dis_mat.mean(axis = 0).sum())
a = new_cal_sumdis(array([1,1,1,1]),MKT_data).plot(title = '距离处理后')
b = MKT_data.plot(title = '距离处理前')

#新核向量寻找函数
def deal_min_dis_vector(mat):
    array_mat = array(mat)
    min_vec = array_mat[0]
    min_distance = float(new_cal_sumdis(min_vec,mat).sum(axis = 1).sum())
    for vector in array_mat:
        vec_dis = float(new_cal_sumdis(vector,mat).sum(axis = 1).sum())
        if vec_dis < min_distance:
            min_vec = vector
            min_distance = vec_dis
        else:
            pass
    return min_vec

#新核心向量
deal_min_vec = deal_min_dis_vector(MKT_data)

#观察以新核心向量计算出地距离分布
deal_dis_mat = new_cal_sumdis(deal_min_vec,MKT_data).sum(axis = 1)
#deal_dis_mat.plot()
mid_ar = np.ones(300) *float(deal_dis_mat.median())
plt.plot(mid_ar)
mean_ar = np.ones(300) *float(deal_dis_mat.mean())
plt.plot(mean_ar)
affect_num = deal_dis_mat.mean() - deal_dis_mat.median()
affect_num

affect_mat = deal_dis_mat - deal_dis_mat.median()
affect_mat.plot()
affect_ar = np.ones(300) * (deal_dis_mat.median() + 3 *affect_num)
plt.plot(affect_ar)

deal_indexA = deal_dis_mat[deal_dis_mat >= deal_dis_mat.median() + 3 * affect_num].index
deal_indexB = deal_dis_mat[deal_dis_mat <= deal_dis_mat.median() - 3 * affect_num].index
for item in deal_indexB:
    if item not in deal_indexA:
        deal_indexA.append(item)
    else:
        pass
deal_index = deal_indexA

#反向KNN，输入原始数据列，寻找最邻近点的数量K个，希望处理的离群点向量值
def Re_KNN(data,KNN_number,aim_series):
    data = array(data)
    label_list = array([vector[-1] for vector in data])
    feature_list = [vector[:-1] for vector in data]
    label_arg = abs((label_list - aim_series[-1])).argsort()
    min_arg = label_arg[:KNN_number + 1]
    min_knn_list = array([feature_list[i] for i in min_arg])
    mean_feature = list(min_knn_list.mean(axis = 0))
    label_value = mean([label_list[i] for i in min_arg])
    mean_point = list(mean_feature)
    mean_point.append(label_value)
    return array(mean_point)

array_MKT_data = array(MKT_data)
deal_target = np.zeros((array_MKT_data.shape[0] - len(deal_index),4))
j = 0
for i in range(0,array_MKT_data.shape[0]):
    if i not in deal_index:
        deal_target[j] = array_MKT_data[i]
        j += 1
    else:
        pass
    for index in deal_index:
        array_MKT_data[index] = Re_KNN(deal_target,5,array_MKT_data[index])
deal_df = pd.DataFrame(array_MKT_data,columns = ['roe','market_cap','pe_ratio','price'])

deal_df['pe_ratio'].plot(title = '高维处理后ROE分布情况')

MKT_data['market_cap'].plot()

#观察回归效果
deal_x = deal_df[['roe','market_cap','pe_ratio']]
deal_y = deal_df['price']
deal_model = sm.OLS(deal_y,deal_x)
deal_result = deal_model.fit()

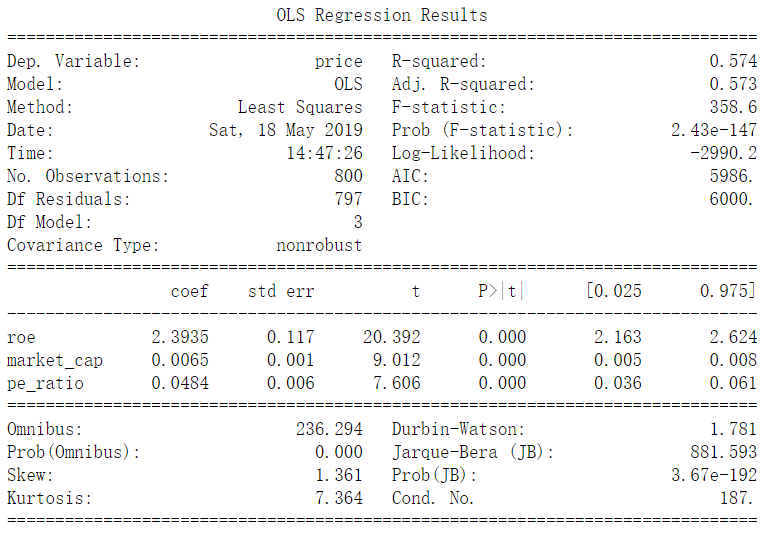
print(deal_result.summary())