以价格系列表示的流程分析工作极具挑战性,通常都需要大量的时间和精力。这会涉及到研究中序列的特点,以及这样一个事实:尽管有大量各种各样的相关出版物,但有时仍然很难找到足以解决某特定问题的编程解决方案。
就算是找到一种适当的脚本或指标,也并不意味着其源代码就不需要调整以适应手头任务。
而且,即便是简单问题的解决方案,这些程序也可能要求使用输入参数,其中要领为开发人员所熟知,用户却未必总是清楚。
这些困难当然不会成为认真研究过程中不可逾越的障碍,但如果有人想证明某个假设,或是单纯地想满足一下好奇心,则这种好奇心在很多时候都会满足不了。所以,我就产生了创建一个通用编程工具的想法,从而方便输入序列主要特性与参数的初步分析。
这种工具的安装要特别简单,而且无需任何输入参数,以最大程度地简化其使用。同时,估得的参数和特性还要充分且明确地反映出所考虑的序列性质。
初步评估特性有助于确定进一步深入研究的方式,或是在早期阶段就驳回任何给定的假设,从而避免用于进一步研究的时间浪费。
众所周知,与自定义软件相比,通用软件的特性少得可怜。这种通用性,几乎一直都是以牺牲整个系统性能为代价的。而本文的主旨则在于:创建一个允许最大程度地方便序列特性初步分析的通用工具。
本文末尾处的 TSAnalysis.zip 文件包括一个 \TSAnalysis 目录,其中包含工作所需的所有文件。解压缩后,要将该目录及其所有内容(无需重命名)复制到 \MQL5\Scripts 目录中。被复制的目录 \TSAnalysis 中包含一个测试脚本 TSAexample.mq5,该脚本可于编译后运行。
该脚本会准备数据,并调用默认浏览器、利用 TSAnalysis 类显示它。要注意的是,为了 TSAnalysis 类的正常运行,要在终端中启用外部 DLLs 的使用。要卸载,只需删除 \TSAnalysis 目录就够了。
序列分析使用的整个源代码会以 TSAnalysis 类表示,且只存在于 TSAnalysis.mqh 文件中。
针对某输入序列采用该类时,它会进行评估,且可显示下述信息:
想要视觉化呈现所考虑的 TSAnalysis 类中获得的结果,则采用一种虚拟呈现的方法,该方法仅负责预先准备信息的显示。
由此,通过 TSAnalysis 类后代中对于此方法的重新定义,就可以任何可能的方式来安排结果的输出,而不仅仅是像基类中一样使用某个 HTML 文件,生成显示图表的数据文件后,即调用 Web 浏览器。
在回顾 TSAnalysis 类之前,我们会以一个测试数据序列为例,说明其使用的结果。下图显示的是 TSAexample.mq5 脚本运行结果。
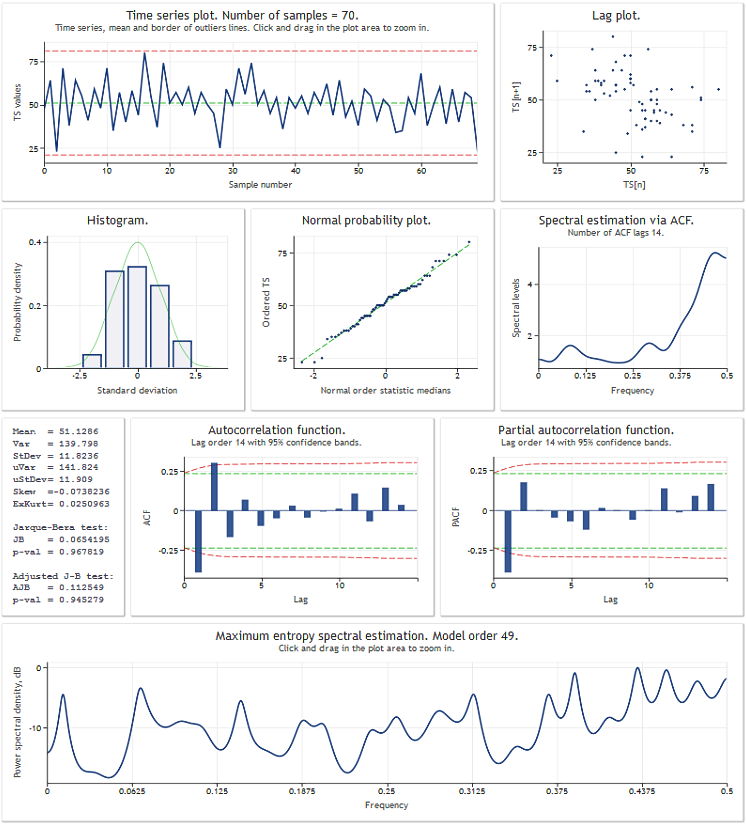
图 1. TSAexample.mq5 脚本运行结果
对 TSAnalysis 类的能力有个粗浅的了解后,现在我们来更详细地研究一下这个类本身。
TSAnalysis 类(参见 TSAnalysis.mqh)仅包括一种可用(公共)方法 - Calc,它负责继虚拟方法显示被调用之后所有必要的计算。该显示方法稍后再谈,现在我们要一步一步地澄清所做计算的要点。
使用 TSAnalysis 类时,针对所研究的输入序列有一些限制。
首先,序列至少要包括八个元素。这种限制很可能不太严格,因为实际应用中很少有必要研究这种短序列。
除了最小序列长度的限制外,此输入序列方差值要求不同于近零。这一要求是鉴于方差值用于进一步的计算中,且不能低于某特定值才能得到稳定结果的事实 。
方差值非常低的序列并不多见,所以,这项限制或许也算不上是严重的缺点。如果序列过短或是存在一个近零方差值,则计算会中断,且日志中会出现一个相关的错误消息。
而对于输入序列的最大允许长度,则还有一个隐含限制。该限制并未明示,取决于在用的计算机性能和内存容量,且按照脚本执行所需时间和 Web 浏览器中绘图结果的速度,以一种完全主观的方式进行确定。我们假设处理由两三千个元素构成的序列的过程中不会造成重大困难。
序列统计参数的计算,将基于 Calc 方法源代码于下方的片断(参见 TSAnalysis.mqh)。
请循下述链接查看所采用算法的描述 "计算方差的算法"。
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // 平均值 sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // 四阶总和 b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // 三阶总和 sum2+=delta*b; // 二阶总和 } . . .
作为此代码片断的执行结果,计算得出下述各值
![]()
其中 n = NumTS 为序列中的元素数。
我们利用得到的值来计算下述参数。
方差和标准差:
![]()
无偏方差和标准差:
![]()
偏斜度:
![]()
峰度。 最小峰度为 1, 正态分布序列的峰度为 3。
![]()
超出峰度:
![]()
这种情况下,最小峰度为 -2,而正态分布序列的峰度则为 0。
按照惯例,在针对序列执行第一次初步拟合优度测试时,都会采用雅克-贝拉统计量(可利用已知的偏斜度和峰度值轻易计算得出)。序列长度增加时,雅克-见拉统计量的统计显著性(p 值)会渐近式趋向反向的卡方分布函数,且有两个自由度。
由此,
![]()
如果序列变短,则以这种方式获得的 p 值一定会有一个显著误差。但这一计算选项却极其常用。原因嘛,不好说 - 可能与其使用的简明公式有关,也可能是因为雅克-贝拉统计量本身并不代表理想的拟合优度,所以更加精确的计算也就没有意义了。
本例中,雅克-贝拉统计量和相关 p 值是根据上述公式按 Calc 方法 (TSAnalysis.mqh) 计算得出的。
此外,还额外计算经过调整的雅克-贝拉测试;
![]()
其中
![]()
经过调整的短序列雅克-贝拉测试会减少以指定方式计算得出的 p 值错误,但却不能完全消除它。
分析的最终结果应包括一个输入序列图,显示对应于均值的线,以及定义限制(超出则认为该值无效且不属于给定序列,离群值)的线。
本例中,上述限制的计算如下:
![]()
![]()
此公式由 S. V. Bulashev 所著的《Statistics for Traders》(面向交易者的统计)一书提供,且参照了 P. V. Novitsky 与 I.A. Zograf 合著的《Estimation of Error in Measurement Results》(针对测量结果中错误的估测)。确定限值之后,并没有处理输入序列的打算;该限值应仅用于信息显示。
除了输入序列图之外,还会显示反映输入序列分布经验估计量的一个直方图。如下定义该直方图的间隔数 (S. V. Bulashev "Statistics for Traders"):
![]()
结果向下取最近的整奇数值。如果所获值小于五,则取 5 为值。
直方图 X 轴 和 Y 轴数据数组的元素数量,对应于所获间隔数上加二,因为直方图左右都添加了一个零值列。
下面列出的是为构建直方图准备数据的一个代码片断(参见 TSAnalysis.mqh)。
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // 柱数 ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // 直方图. X-轴 for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // 直方图. Y-轴 . . .
在上述代码中:
利用该计算方法,X 轴值会按标准差单位表示,而 Y 轴值则会与概率密度对应。
出于构建带有正态分布轴的图表的目的,将按升序排列的输入序列作为 Y 轴值使用。Y 轴与 X 轴值的数量应该相等。想要计算 X 轴值,就必须首先如均匀分布法中一样找到中间值:
![]()
![]()
![]()
之后,它们还将通过逆正态分布函数的方法,用于计算 X 轴值(参见 ndtri 方法)。
想要创建自相关函数 (ACF) 图 、部分自相关函数 (PACF) 图并利用最大熵值法计算谱估值,则要为输入序列找到自相关函数值。
我们会如下撰述,定义要在 ACF 图与 PACF 图上显示的值的数量:
![]()
![]()
![]()
按指定方式确定的值数量,已足够图上自相关函数的显示。但为了进一步用于谱估值的计算,建议将计算得出的 ACF 值的数量调高一些,本例中则是等同于所采用自回归模型的阶。
IP 模型阶通过所获的 NLags 值定义:
![]()
![]()
想要把确定谱估值模型最优阶的流程规范化,很难办到。低阶模型会带来极其平滑的结果,而高阶模型则极有可能导致取值范围太大且不稳定的谱估值。
此外,模型阶还会受到输入序列性质的影响,由此,利用上述公式确定的 IP 阶在某些情况下会过高,某些情况下又会过低。遗憾的是,尚未找到确定所需模型阶的有效方法。
因此,应为输入序列确定等同于 IP 模型阶(用于序列的谱估值)的 ACF 值。
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // 自动相关性 } . . .
此源代码片断(参见 TSAnalysis.mqh)阐明了自相关函数 (ACF) 的计算过程。计算结果位于 cor[] 数组内。大家可以看到,首先是计算一个零自相关系数,然后才是循环中剩余系数的计算和标准化。实施该标准化后,此零系数会始终等于一,所以也就无需将其存储于 cor[] 数组中。
此数组中包含的系数数量等于从第一个开始的 IP。如果计算 ACF,则会用到 TSCenter[] 数组;它所包含的元素输入序列,都要减去平均值。
想要缩短计算 ACF 所需的时间,可以使用集成快速转换算法的方法,比如 FFT。但本例中计算 ACF 所需的时间完全可以接受,所以很可能也就无需再将编辑代码复杂化了。
利用获取的相关系数值,即可轻松构建 ACF 图(相关图)。要能在此图上显示 95% 的置信带,则可利用下述公式计算出它们的值。
针对用于随机性测试的带:
![]()
针对用于确定 ARIMA 模型阶的带:
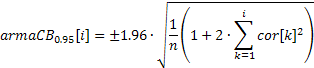
第一种情况下的置信带值会是恒定的;而第二种情况下,则会随着自相关系数的增长而增长。
仅反映频率分布总体趋势的一种非常平滑的输入序列频率响应,有时可能也很吸引人。比如说,低频或高频范围内的显著上升、中频的主导等等。
明智的做法是按线性标度显示该频率响应,以突显主导频率范围。这种幅度-频率响应 (AFR) 可根据之前获取的自相关系数进行标绘。至于 AFR 的计算,我们则会采用与 ACF 图上显示数相等的系数数量。
只要此数不大,作为结果获取的谱估计就应该相当平滑。
这种情况下,序列的频率响应即可如下通过自相关系数的方式进行表达:
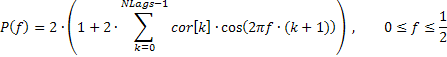
下面列出的,即为根据提供的公式进行 AFR 计算所采用的代码片断(参见 TSAnalysis.mqh)
. . . n=320; // X-点数量 ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Y-轴频谱 } . . .
要注意的是:为了进一步平滑,上述代码上的相关系数值,要乘以三角窗函数。
至于更加详尽的频谱分析,则选择最大熵值法作为另一折衷办法。通用的谱估值方法的选择非常困难。大家也都清楚与经典非参数频谱分析方法有关的各种缺点。
此类方法利用快速傅里叶变换算法即可轻松实施,而周期图与相关图方法都是很好的例证。但尽管结果稳定性高,这些方法还是需要非常长的输入序列才能获得足够的分辨力。与之相比,谱估值的参数方法(比如自回归方法)则可确保短序列高得多的分辨率。
遗憾的是,使用它们时不仅要考虑这些方法具体实施的特点,还要考虑输入序列的性质。同时,要确定最优 AR 模型阶也是相当困难,其中的增长会导致分辨力增长,但却会得到分散结果。如果使用了非常高阶的模型,则上述方法开始给出不稳定结果。
不同谱估值算法的特性比较,请参阅由 S. L. Marple 编著的《Digital Spectral Analysis with Applications》(应用程序数字频谱分析)。正如前面提到的,本例中选择最大熵值法。同其它自回归方法相比,该方法导致的分辨力可能最低,而之所以选择它,就是考虑到获取更加稳定的谱估值。
我们研究研究自回归谱估值计算的阶。之前我们已探讨过该模型阶的选择,所以,我们假定模型阶已选定为与已完成计算的 IP 和 IP 自相关系统系数 cor[] 相等。
想要利用已知自相关系数获取自回归系数,则将莱文逊-德宾算法作为莱文逊递归方法实施使用。
//----------------------------------------------------------------------------------- // 为自动相关序列 R[] 计算莱文逊-德宾递归 // 并返回自动回归系数 A[] 和部分自动相关 // 系数 K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
它具有三个输入参数:所有三个参数都是对数组的引用。调用此方法时,输入自相关系数应置于第一个数组 R[] 中。在计算过程当中,这些值保持不变。
获取的自相关系数则会放入数组 A[] 中。此外,数组 K[] 将包含与取反号的自回归模型反射系数相等的部分自相关函数值。模型阶不作为一个输入参数传递;它被假设为与输入数组 R[] 中的元素数量相等。
因此要求输出数组大小不可小于输入数组大小;此函数内并不检查该要求的满足。计算完成时,零自回归系数和部分自回归函数的零系数都不会保存于 A[] 和 K[] 数组中。
它们被当做始终等于一。因此,就像输入序列中一样,输出数组也会包含索引从 1 到 IP (不要与索引从 0 开始的数组混淆)的系数。
取得的部分自相关函数的值,仅用于各个标绘上的显示;而自回归系数则会充当频率响应估值计算的基础,并按下述公式定义:
![]()
频率响应在 0 到 0.5 的范围内,针对 4096 个标准化频率值进行计算。利用上述公式进行的 AFR 值直接计算,会耗用过多的时间。而利用快速傅里叶变换算法来计算复杂指数之和,则会大幅缩短此时间。
为此,Calc 方法采用快速哈特利变换 (FHT) 来替代快速傅里叶变换。
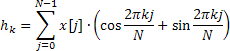
哈特利变换并不涉及复杂运算,且输入与输出序列均有效。仅需要一个附加系数 1/N,即可利用相同的公式来计算逆哈特利变换。
在一个有效的输入序列中,此变换的系数与傅里叶变换的系数之间有一个简单的连接。
![]()
有关快速哈特利变换算法的信息,请见 "FXT 算法库" 和 "离散傅里叶与哈特利变换"。
在给定的实施中,快速哈特利变换函数是通过 fht 方法表示的。
//----------------------------------------------------------------------------------- // 按频率抽取 (DIF) 的快速哈特利变换 (FHT) 基2算法. // Length 等于 N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
调用此方法时,输入数据数组 f[] 的一个引用、以及定义变换长度 N = 2 ** ldn 的无符号整数 ldn 会被传递到输入中。数组 f[] 的大小不得小于变换长度 N。请牢记:此函数内没有针对于此的检查。还要记住:变换结果存储于放置输入数据的数组内。
变换后,并不存储输入数据本身。在所研究的 Calc 方法中,长度 N=8192 的变换是用于计算 4096 AFR 值。变换平方幅值和取倒数计算之后,获取的结果就会被标准化为其最大值,且以对数标度。
此外,Calc 方法就没有什么重大特点了;必要时,可参照 TSAnalysis.mqh 更仔细地研究其实施。
获取和为作为计算结果准备显示的所有值,均保存于作为 TSAnalysis 类成员的变量中。因此,在调用虚拟方法显示以呈现结果时,它们无需作为自变量传递。
前面提到过,显示方法是作为虚拟声明的。所以,通过对其重新定义,即可以实施要求的方法,以显示与所提议的有所不同的计算结果。所提议的 TSAnalysis 类中的可视化,是通过数据文件准备和调用数据显示 Web 浏览器的方式执行的。
要想 Web 浏览器能够显示该数据,则要用到与其它项目文件在同一个目录下的 TSA.htm 文件。这种显示图形信息的方法,之前在《HTML 中的图形与图表》一文中讲到过。
显示方法的 TSAnalysis 类负责用于字符串类型变量中显示的所有计算结果的格式化和保存(参见 TSAnalysis.mqh)。按这种方式生成的一条长线,仅需一步就可保存到 TSDat.txt 中。而此文件的创建,以及将数据保存其中,则是利用标准的 MQL5 工具来执行。因此,该文件于 \MQL5\Files 目录下创建。
之后,再通过调用外部系统函数,将其移至该项目的目录。随后,再调用一个显示 TSA.htm (使用源于 TSDat.txt 的数据)的 Web 浏览器。因为系统函数是在显示方法中调用,所以要在终端启用外部 DLLs 才能处理 TSAnalysis 类。
包含于 TSAnalysis.zip 存档中的 TSAexample.mq5,是 TSAnalysis 类的一个使用示例。
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // 脚本程序起始函数 //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
您看到了,类的引用相当简单;如果有一个准备好的、包含输入序列的数组,则将其传递给 Calc 方法分析不会太费事。此外,您要记得调用删除以释放内存。此脚本的运行结果,本文开头即已提供。
为了展示谱估值产生的效能,我们再来看几个会使用生成序列的示例。
首先,我们会使用一个由两条正弦曲线构成的序列。
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
下图演示的是该序列的频率响应估值。
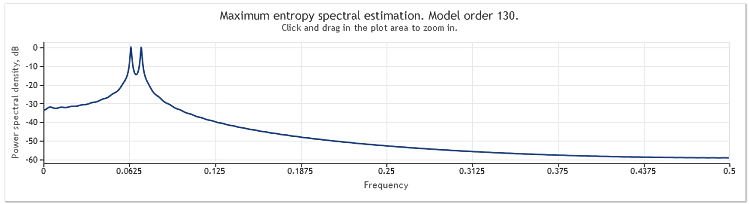
图 2. 谱估值两条正弦曲线
尽管两条正弦曲线均可清楚观测到,但放大图表上感兴趣的区域,我们才能发现波峰位于 0.0637 和 0.0712 频率处。换而言之,它们与真实值有某种程度的不同。如是由一条正弦曲线构成的序列,则不会观测到估值的这种乖离。我们将这种现象视为频谱分析的选定方法效应。
我们通过向序列中添加一个随机组件,以将任务进一步复杂化。为此,就会用到一个表示为 RNDXor128 类的伪随机序列生成器,它随附于文末的 RNDXor128.zip 文档中。
下述代码片断用于生成一个测试信号。
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
本例中是将带有正态分布和单位方差的一个随机信号添加到两条正弦曲线。
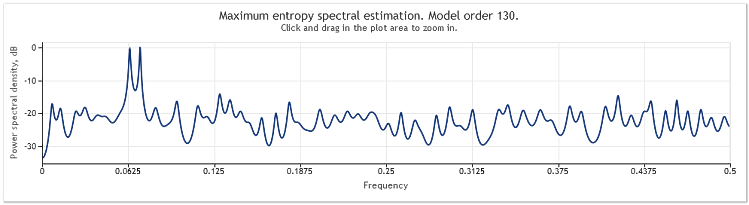
图 3. 谱估值两条正弦曲线加一个随机信号
本例中的正弦曲线保持清楚可辨。
随机组件幅度增加五倍会导致正弦曲线显著模糊。
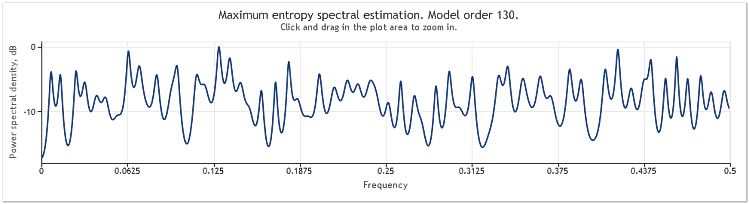
图 4. 谱估值两条正弦曲线加一个大幅度的随机信号
当序列长度从 400 增至 800 个元素时,正弦曲线再一次变得清楚可辨。
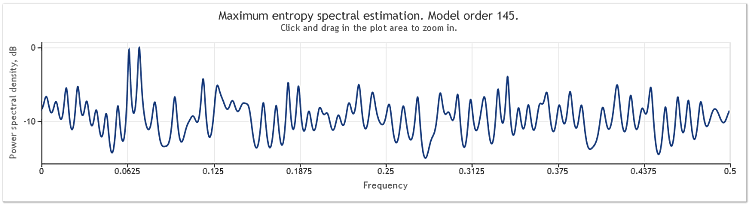
图 5. 两条正弦曲线加一个大幅度的随机信号N=800
自回归模型阶借此由 130 增至 145。序列长度的增加产生更高阶模型,并造成谱估值的分辨力增加 - 图表峰值变得显著锐化。
两年内(2009 与 2010) EURUSD, D1 报价的谱估值可如下呈示。

图 6. EURUSD 报价2009-2010. 周期 D1
该输入序列由 519 个值构成,而从图上看,模型阶似乎有 135 个。
可以看出,此谱估值包含大量的明显峰值。但单凭此估计,并不足以确定这些峰值是否为报价的周期分量。
频率响应中峰值的出现,既可由报价中存在的高级随机分量导致,亦可由所涉序列的明示非定常性造成。
因此,在得出有关周期分量存在的最终结论之前,最好是利用源自另一序列片断或另一时间框架的数据,来验证获得的结果。此外,研究周期性重现时,还可以尝试使用序列差异替代序列本身。
因为本文中采用的谱估值方法基于自相关系数,所以,应用该方法时,输入序列的平均值总像是从序列中删除了。通常来讲,从输入序列中删除某恒定分量绝对有必要,但是,在使用自回归方法时,这种删除在某些情况下可造成低频范围内谱估值的失真。
这种失真的示例,请见 S. L. Marple 编著的《Digital Spectral Analysis with Applications》(应用程序数字频谱分析)一书中的“谱估值相关结果汇总”一章末尾。本例中,所采用的频谱分析方法让我们别无选择,所以只需牢记:谱估值始终都相对于带有删除平均值的序列执行。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...