随着电脑性能的不断提升,外汇交易人员和分析师有了应用依托于大量计算机资源的高度成熟和复杂的数学算法的更多可能性。但仅仅依靠充足的电脑资源并不能解决交易人员的问题。高效的市场报价分析算法同样是必不可少的。
目前,交易人员积极将诸如数理统计、经济学和计量经济学等领域提供的大量方法、模型以及完善高效的算法运用于市场分析中。通常而言,这些都是基于研究序列稳定性及其分布规律正态化的假设建立的标准参数化方法。
然而众所周知的是,外汇报价并不是稳定和具有正态分布规律的序列。因此,在分析报价时,我们无法使用数理统计、计量经济学等“标准”参数化方法。
在《Box-Cox Transformation and the Illusion of Macroeconomic Series "Normality"》[1](Box-Cox 变换和宏观经济系列“正态性”的幻觉)一文中,A.N. Porunov 如下写道:
“经济分析师常常需要处理基于这样或那样的原因而未通过正态性测试的统计数据。在这种情况下,我们有两个选择:要么转向非参数化的方法,这种方法要求我们接受过大量的数学训练;或者是运用特殊技巧,从而将原来的“不规则”统计数据转换为“规范”统计数据,这也是一项相当复杂的任务”。
尽管 A.N.Porunov 的引用语针对的是经济分析师,它可以完全归因于使用数理统计和计量经济学的参数化方法分析“不规则”外汇报价的尝试。这些方法的绝大多数被开发出来用于分析具有正态分布规律的序列。而在大多数情况下,初始数据“不规则”的事实被忽略。此外,上述方法通常不仅要求初始序列呈正态分布,还要求其稳定。
回归、离差(方差分析)以及其他一些分析类型可称为要求初始数据呈正态性的“标准”方法。列出所有在正态分布规律方面具有局限性的参数化方法是不可能的,因为它们占据了计量经济学中非参数化方法以外的全部。
平心而论,应该说“标准”参数化方法对于初始数据分布规律相对于标准值的偏差具有不同的敏感度。因此,与“正态性”的偏差在此类方法的使用中不一定会导致灾难性结果,当然,也不会提高所获结果的准确性和可靠性。
所有这些引发了一个问题:分析和预测报价是否有必要转向非参数化方法。然而,参数化方法仍然有极大的吸引力。这可以通过它们的盛行以及大量的数据、现成算法和应用示例得到解释。要正确使用这些方法,必须妥善处理与初始序列相关的至少两个问题 - 不稳定和“不规则”。
虽然我们无法影响初始序列的稳定性,但我们可以尝试使其分布规律更接近于正态分布。要解决这个问题,有多种变换可以使用。其中最有名的变换在《The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses》[2](Box-Cox 变换技巧在经济和统计分析中的运用)一文中进行了简要说明。在本文中,我们仅讨论其中之一 - Box-Cox 变换[1]、[2]、[3]。
在此我们要强调的是,和任何其他变换类型一样,使用 Box-Cox 变换只能令初始序列的分布规律或多或少地更接近于正态分布。意即,使用此变换并不能保证结果序列具有正态分布规律。
对于长度为 N 的原始序列 X
![]()
其带有一个参数的 Box-Cox 变换如下所示:
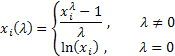
其中 ![]() 。
。
如您所见,此变换仅有一个参数 - lambda。如果 lambda 值等于 0,则进行初始序列的对数变换;如果 lambda 值不等于 0,则变换为幂律。如果 lambda 参数等于 1,即使序列移位,由于从其每个值中减去了单位元素,初始序列的分布规律保持不变。
取决于 lambda 的值,Box-Cox 变换包含以下特例:
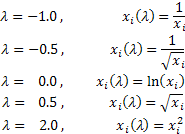
Box-Cox 变换的使用要求所有输入序列值为正且不等于 0。如果输入序列不满足这些要求,可通过保证其所有的值为“正性”的量将其移入正区。
现在我们只讨论一个参数的 Box-Cox 变换,以适当的方式为其准备输入数据。为了避免在输入数据中出现负值和 0 值,我们将总是找到输入序列中的最小值,将其从额外执行了等于 1e-5 的小移位的序列的每个元素中减去。这样一个额外的移位对于提供到正区的有保证的序列位移是必要的,如果其最小值等于 0。
实际上,没有必要对“正”序列应用此移位。尽管如此,我们将使用同一算法,以在变换期间自乘时降低获得极大值的可能性。因此,任何输入序列将在移位后分布于正区,并具有接近于 0 的最小值。
图 1 显示不同 lambda 参数值下的 Box-Cox 变换曲线。图 1 取自《Box-Cox Transformations》[3](Box-Cox 变换)一文。图表上的水平栅格基于对数刻度。
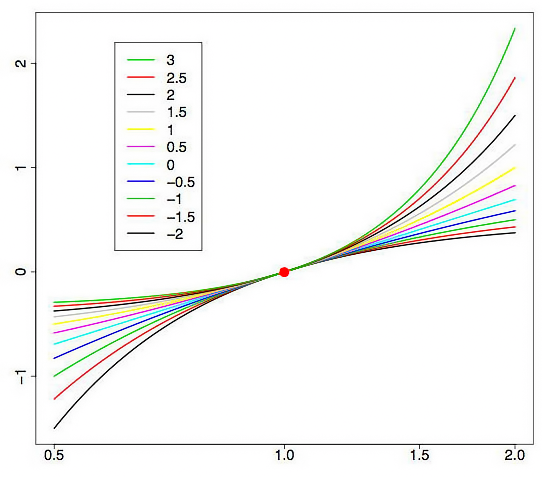
图 1. 各种 lambda 参数值下的 Box-Cox 变换
我们可以看到,初始分布的“尾部”可以“拉伸”或“缩起”。图 1 中的上曲线对应的 lambda 值为 3,下曲线对应的 lambda 值为 -2。
为了使结果序列的分布规律尽可能地接近于正态分布,必须选择 lambda 参数的最优值。
确定此参数的最优值的一种方法是最大化对数似然函数:
![]()
其中
![]()
这意味着我们需要选择此函数达到最大值的 lambda 参数。
《Box-Cox Transformations》[3](Box-Cox 变换)一文简要阐述了确定此参数的最优值的另一种方法,该方法基于对正态分布函数的分位数和排序变换序列之间的相关系数的最大值的搜索。很有可能,我们能够找到 lambda 参数的其他最优化方法,但我们首先来讨论之前提到的对数似然函数的最大值搜索。
我们有不同的方法来找到它。例如,我们可使用一个简单搜索。为此,我们应计算在一个选定的范围内以小距改变 lambda 参数值的似然函数值。同时,我们应选择最优 lambda 参数,使得似然函数在该参数值下达到最大值。
间距将决定 lambda 参数最优值计算的精确度。间距越小,精确度越高,但所需的计算量在这种情况下也将按比例增加。有多种搜索函数最大值/最小值的算法、遗传算法以及其他一些方法可用于提高计算的效率。
Box-Cox 变换最重要的任务之一是将输入序列的分布规律简化为“正态”形式。让我们试着在此变换的帮助下找出这个问题的解决方法。
为避免任何分心和不必要的重复,我们将使用 Powell 法的函数最小值搜索算法。此算法在《Time Series Forecasting Using Exponential Smoothing》(用指数平滑预测时间序列)和《Time Series Forecasting Using Exponential Smoothing (continued)》(用指数平滑预测时间序列 (续))中进行了说明。
我们应创建 CBoxCox 类用于搜索变换参数的最优值。在此类中,上述似然函数将作为一个目标实现。PowellsMethod 类 [4], [5] 用作直接实现搜索算法的基本类。
//+------------------------------------------------------------------+ //| CBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CBoxCox class | //+------------------------------------------------------------------+ class CBoxCox:public PowellsMethod { protected: double Dat[]; // Input data double BCDat[]; // Box-Cox data int Dlen; // Data size double Par[1]; // Parameters double LnX; // ln(x) sum public: void CBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CBoxCox::CalcPar(double &dat[]) { int i; double a; //--- Lambda initial value Par[0]=1.0; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(BCDat,Dlen); LnX=0; for(i=0;i<Dlen;i++) { //--- input data a=dat[i]; Dat[i]=a; //--- ln(x) sum LnX+=MathLog(a); } //--- Powell optimization Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CBoxCox::func(const double &p[]) { int i; double a,lamb,var,mean,k,ret; lamb=p[0]; var=0; mean=0; k=0; if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;} // Lambda > 5.0 else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0 //--- Lambda != 0.0 if(lamb!=0) { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb; //--- average value calculation mean+=BCDat[i]/Dlen; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { //--- Box-Cox transformation BCDat[i]=MathLog(Dat[i]); //--- average value calculation mean+=BCDat[i]/Dlen; } } for(i=0;i<Dlen;i++) { a=BCDat[i]-mean; //--- variance var+=a*a/Dlen; } //--- log-likelihood ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX; return(k+ret); } //------------------------------------------------------------------------------------
要找出 lambda 参数的最优值,现在我们只需要通过将所述类与指向包含输入数据的数组的链接一起提供来参照该类的 CalcPar 方法。我们可通过参照 GetPar 方法获得得到的参数最优值。正如之前所述,输入数据必须为正。
PowellsMethod 类实施有多个变量的函数最小值搜索算法,但在我们的示例中,仅有一个参数得到优化。这使得 Par[] 数组的维度等于 1。这意味着数组只包含 1 个值。理论上,我们可以在这个示例中使用标准变量来代替参数数组,但这需要更改 PowellsMethod 基类代码。据推测,如果我们使用仅包含 1 个元素的数组编译 MQL5 源代码,不会产生任何问题。
我们应注意 CBoxCox::func() 函数限制 lambda 参数允许值范围的事实。在我们的示例中,允许值限制在 -5 到 5 的范围内。这样做是为了避免在取输入数据的 lambda 次幂时获得过大或过小的值。
此外,如果我们在最优化的过程中获得过大或过小的 lambda 值,这可能意味着序列对于选定的变换类型用处不大。因此,在计算 lambda 值时,不超出某合理范围在任何情况下都不失为明智的做法。
让我们编写一个测试脚本,以执行我们使用 CBoxCox 类生成的伪随机序列的 Box-Cox 变换。
下面是这样一个脚本的源代码。
//+------------------------------------------------------------------+ //| BoxCoxTest1.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input array preparation ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
在显示的脚本中,一个具有指数分布规律的伪随机序列被用作输入变换数据。序列长度在变量 n 中设置,本例中为 1600 个值。
RNDXor128 类(George Marsaglia,Xorshift RNG)被用于生成伪随机序列。此类在《Analysis of the Main Characteristics of Time Series》[6](时间序列的主要特性分析)一文中进行了说明。Box-Cox-Tranformation_MQL5.zip 档案中包含了 BoxCoxTest1.mq5 脚本编译所需的全部文件。要成功编译,这些文件必须位于一个目录下。
在执行显示的脚本时,输入序列形成、移至正值区,同时 lambda 参数的最优值搜索执行。然后包含获得的 lambda 值以及搜索算法执行次数的消息显示。作为结果,变换序列将在 bcdat[] 输出数组中创建。
在其当前形式下,此脚本仅允许准备变换序列以供进一步使用,而没有实施任何更改。在撰写本文时,《Analysis of the Main Characteristics of Time Series》[6](时间序列的主要特性分析)一文中阐述的分析类型被选择用于评估变换结果。本文中并未列示用于此目的的脚本,以减少给出的代码量。下面只给出了现成的图形化分析结果。
图 2 显示在正态分布刻度下 BoxCoxTest1.mq5 脚本中使用的具有指数分布规律的伪随机序列的直方图和图表。Jarque-Bera 测试结果 JB=3241.73、p= 0.000。我们可以看到,输入序列完全不是“正态”的,且正如预期的那样,其分布近似于指数分布。
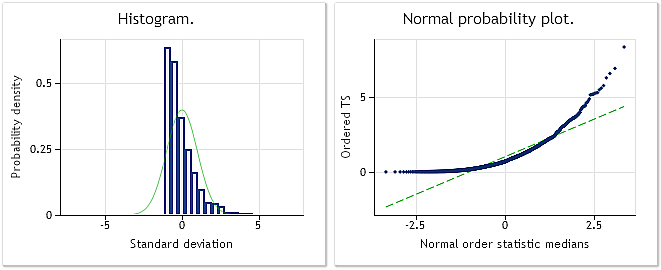
图 2. 具有指数分布规律的伪随机序列。Jarque-Bera 测试 JB=3241.73,р=0.000。
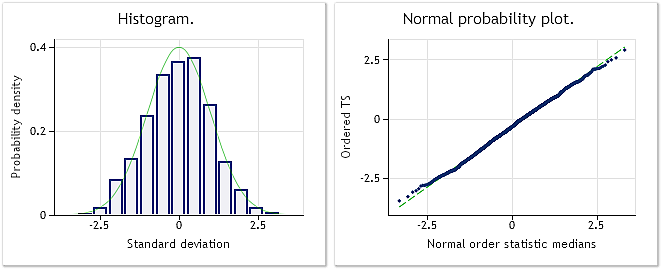
图 3. 变换序列。Lambda 参数=0.2779,Jarque-Bera 测试 JB=4.73,р=0.094
图 3 显示了变换序列分析的结果(BoxCoxTest1.mq5 脚本,bcdat[] 数组)。变换序列的分布规律明显更接近于正态分布,这也通过 Jarque-Bera 测试结果 JB=4.73、p=0.094 得到了证实。获得的 lambda 参数值=0.2779。
在这个示例中,Box-Cox 变换证明了本身具有足够的合适性。似乎结果序列变得明显更接近于“正态”分布,且 Jarque-Bera 测试结果从 JB=3241.73 降为 JB=4.73。这并不奇怪,因为所选序列显然很适合这种类型的变换。
我们研究一下伪随机序列 Box-Cox 变换的另一个示例。考虑到 Box-Cox 变换的幂律性,我们应为其创建一个“合适”的输入序列。为此,我们需要生成一个伪随机序列(其分布规律接近正态分布规律),然后取其所有值的 0.35 次幂使其变形。可以预期,Box-Cox 变换将返回原始正态分布至高精确度的输入序列。
下面是 BoxCoxTest2.mq5 text 脚本的源代码。
此脚本与上一个脚本的唯一不同之处在于,它生成了另一个输入序列。
//+------------------------------------------------------------------+ //| BoxCoxTest2.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" #include "RNDXor128.mqh" CBoxCox Bc; RNDXor128 Rnd; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; //--- data size n=1600; //--- input data array ArrayResize(dat,n); //--- transformed data array ArrayResize(bcdat,n); Rnd.Reset(); //--- random sequence generation for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm(); //--- input data shift min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35); //--- optimization by lambda Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda; } else { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]); } // Lambda == 0.0 //-- dat[] <-- input data //-- bcdat[] <-- transformed data } //-----------------------------------------------------------------------------------
显示的脚本生成了具有正态分布规律的伪随机输入序列。将此序列移位至正值区后,取其所有元素的 0.35 次幂。在完成脚本的编译操作后,dat[] 数组包含输入序列,而 bcdat[] 数组包含变换序列。
图 4 显示因取 0.35 次幂而失去其原始正态分布规律的输入序列的特性。在这种情况下,Jarque-Bera 测试为 JB=3609.29、p= 0.000。
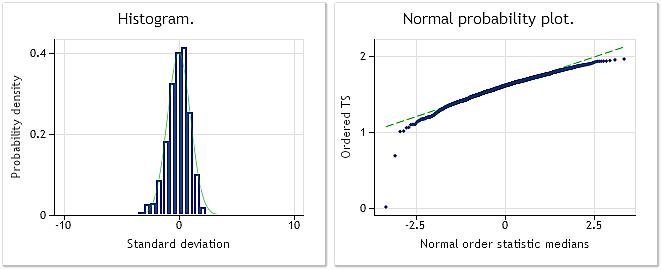
图 4. 伪随机输入序列。Jarque-Bera 测试 JB=3609.29、p=0.000。
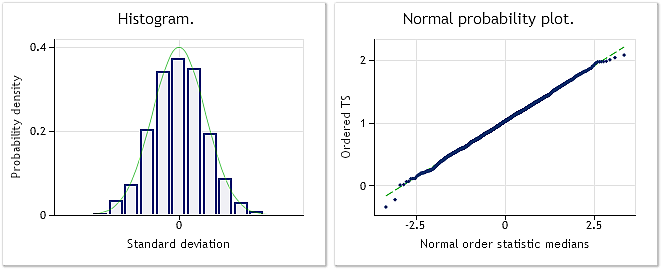
图 5. 变换序列。Lambda 参数=2.9067,Jarque-Bera 测试 JB=0.30、р=0.859
如图 5 所示,变换序列具有十分接近于正态分布的分布规律,这也通过 Jarque-Bera 测试值 JB=0.30、p=0.859 得到了证实。
我们使用的这些 Box-Cox 变换示例展示出极为理想的结果。但我们不应该忘记,对于此变换而言,我们在两个示例中都使用了最为便利的序列。因此,这些结果只能视为对我们所创建算法的性能的证实。
在证实了实施 Box-Cox 变换的算法的正常性能后,我们应尝试将其应用于实际的外汇报价,以使它们呈现我们所希望的正态分布规律。
我们将使用在《Time Series Forecasting Using Exponential Smoothing (continued)》 [5](用指数平滑预测时间序列 (续))一文中说明的序列作为测试报价。它们位于 Box-Cox-Tranformation_MQL5.zip 档案的 \Dataset2 目录下并提供实际报价,其 1200 个值保存在相应的文件中。解压缩的 \Dataset2 文件夹必须位于客户端的 \MQL5\Files 目录下,以提供对这些文件的访问。
我们假设这些报价不是平稳序列。因此,我们不会将分析结果的适用性上升到所谓的普适性,而仅仅将其视为此特殊有限长度序列的特性。
此外,须再次提及的是,如果不具备平稳性,同一货币对的不同报价片段所遵循的分布规律将大相庭径。
我们来创建一个脚本,以从文件中读取序列值和执行其 Box-Cox 变换。相较上文给出的测试脚本,所不同处仅在于形成输入序列的方法。下面是这个脚本的源代码,BoxCoxTest3.mq5 脚本则位于随附档案中。
//+------------------------------------------------------------------+ //| BoxCoxTest3.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CBoxCox.mqh" CBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],bcdat[],lambda,min; string fname; //--- input data file fname="Dataset2\\EURUSD_M1_1200.txt"; //--- data reading if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- transformed data array ArrayResize(bcdat,n); //--- input data array min=dat[ArrayMinimum(dat)]-1e-5; for(i=0;i<n;i++)dat[i]=dat[i]-min; //--- lambda parameter optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); PrintFormat("Iterations= %i, lambda= %.4f",Bc.GetIter(),lambda); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;} else {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);} // Lambda == 0.0 //--- dat[] <-- input data //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //-----------------------------------------------------------------------------------
所有值(在我们的示例中为 1200)从报价文件导入此脚本中的 dat[] 数组,报价文件的名称在 fname 变量中设置。接下来,初始序列移位、最优参数值搜索和 Box-Cox 变换以上文所述方式执行。待脚本执行后,变换结果位于 bcdat[] 数组中。
从显示的源代码可以看出,脚本选择 EURUSD M1 报价序列用于变换。原始和变换序列的分析结果在图 6 和图 7 中显示。
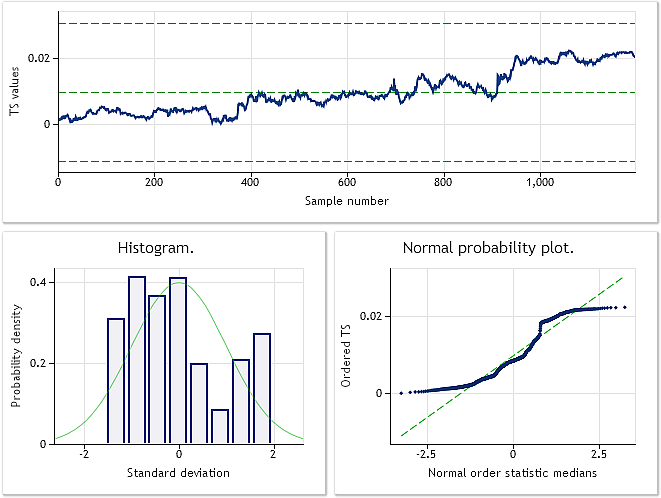
图 6. EURUSD M1 输入序列。Jarque-Bera 测试 JB=100.94、p=0.000。
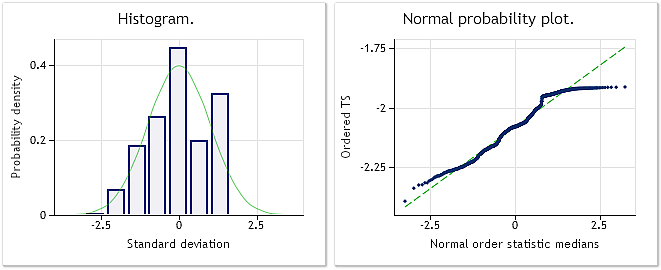
图 7. 变换序列。Lambda 参数=0.4146,Jarque-Bera 测试 JB=39.30、р=0.000
根据图 7 中显示的特性,EURUSD M1 报价变换的结果没有之前得出的伪随机序列变换的结果那样鲜明。 虽然 Box-Cox 变换被认为具有足够的普适性,但它无法处理所有类型的输入序列。例如,期望通过幂律变换将双顶分布转换为正态分布是不切实际的。
虽然很难将图 7 中显示的分布规律视作正态分布,我们仍然能够看到 Jarque-Bera 测试值如前例所示的那样显著下降。原始序列的 JB=100.94,变换后 JB=39.30。这表示分布规律在经过变换后某种程度上接近于正常分布。
在变换其他不同的报价片段后得到了大致相同的结果。每一次,Box-Cox 变换以较大或较小的程度使分布规律接近于正态分布。但从未成为正态分布。
使用各种报价变换进行的一系列试验可得出完全可预期的结论 - Box-Cox 变换使外汇报价的分布规律接近于正态分布,但它无法保证使变换数据的分布规律达到真正的正态性。
执行仍未使原始序列成为正态分布序列的变换是否合理?这个问题没有确切的答案。在每个特定情形下,我们应就 Box-Cox 变换的需要做出个别决策。在本例中,这主要取决于报价分析中使用的参数化方法的类型,以及这些方法对初始数据偏离正态分布规律的敏感度。
图 6 的上半部分显示了在 BCTransform.mq5 脚本中使用的 EURUSD M1 原始序列的图表。从图中我们可以很容易看出,它的值几乎沿整个序列均匀增加。通过执行第一次近似,我们可以得出序列包含线性趋势的结论。这种“趋势”的出现表明我们应在执行各种变换和分析得到的序列之前去除趋势。
从分析输入序列去除趋势或许不应被视为完全适于所有情形的方法。但我们假设要分析图 6 中显示的序列,从中找出周期(或循环)部分。在这种情形下,我们在定义趋势的参数后必定能够从输入序列中去除线性趋势。
去除线性趋势将不会影响对周期部分的检测。取决于选定的分析方法,这种做法甚至可能是有益的,在某种程度上使这样的分析结果更加精确可靠。
如果我们确定趋势去除在某些情形中可能有益,则有关 Box-Cox 变换如何处理去除趋势的序列的探讨可能是有意义的。
在任何情形下,我们在去除趋势时需要决定用于趋势近似的曲线。这可以是一条直线、高阶曲线或移动平均线等。在本例中,让我们选择 - 如果我可以这样说 - 为避免因最优曲线的选择问题而分心的极端形式。我们将使用原始序列的增量,即当前值与之前值的差值而不是原始序列本身。
在我们讨论增量分析时,我们不得不提到一些相关问题。
在许多文章和论坛里,向增量分析转变的必要性的证明方式可留下有关这种转变性质的错误印象。向增量分析的转变往往被描述成一种变换,这种变换能够将原始序列转换为平稳序列或是使其分布规律正态化。但事实果真如此吗?让我们试着来回答这个问题。
我们应从这样一个事实开始,即转向增量分析的本质为一个十分简单的理念 - 将原始序列分为两个部分。我们可以证明如下。
假设我们有输入序列
![]()
不管出于什么原因,我们决定将其划分为一个趋势以及将趋势值从原始序列的元素中去除后出现的剩余元素。假设我们决定在趋势近似中使用平滑周期等于两个序列元素的简单移动平均线。
这样的移动平均数可通过两个相邻序列元素的和除以 2 计算得出。在这种情况下,从原始序列去除平均数后的剩余元素等于同样的相邻元素的差除以 2。
我们将上述平均数值命名为 S,剩余值命名为 D。为更加一目了然,我们将常量因子 2 移至等式左边,我们将得到如下所示的新等式:
![]()
在完成这一相当简单的变换后,我们将原始序列分成了两个部分,其中一个部分是相邻序列值的和值,另一部分则由相邻序列值的差值组成。这些正是我们称之为增量的序列,而和值形成趋势。
就这一点而言,将增量作为原始序列的一部分考虑将更为合理。因此,我们不应忘记,如果我们转向增量分析,则由和值定义的序列的另一部分通常会被无视;当然,除非我们不对其进行单独分析。
要了解我们可以从序列的这种划分中获得何种益处,最简单的方法便是应用波谱法。
我们可以从上述表达式直接得出,S 部分是使用脉冲特性 h=1.1 的低频滤波器对原始序列进行滤波的结果。相应地,D 部分是使用脉冲特性 h=-1.1 的高频滤波器进行滤波的结果。图 8 在名义上显示了这种滤波器的频率特性。
图 8. 幅频特性
假设我们从对序列本身的直接分析转向其差值分析。在此,我们可以预期什么呢?在这种情况下,我们有多种选择。我们仅对其中的一部分简要加以介绍。
类似地,对于任何其他趋势组合、短期趋势及干扰噪音等,我们可以得出有关转向差值分析的结果的结论。但在任何情形中,转向差值分析将不会得出分析过程的平稳形式,也不会正态化分布过程。
基于上述内容,我们可以得出:在转向差值分析后序列不会自动“改良”。我们相信,在某些情形中最好是分析输入序列以及其相邻值的差值及和值,以获得对输入序列更清晰的认识,而有关此序列性质的最终结论应基于对获得的所有结果的综合考量作出。
让我们回到本文的主题,看一看在转向图 6 中显示的 EURUSD M1 序列的增量分析后 Box-Cox 变换如何运作。为此,我们将使用上文中给出的 BoxCoxTest3.mq5 脚本,在计算来自文件的这些序列值后,我们将使用差值(增量)替换脚本中的序列值。由于我们未对该脚本的源代码进行其他更改,再次列示没有任何意义。我们将只显示其功能分析的结果。
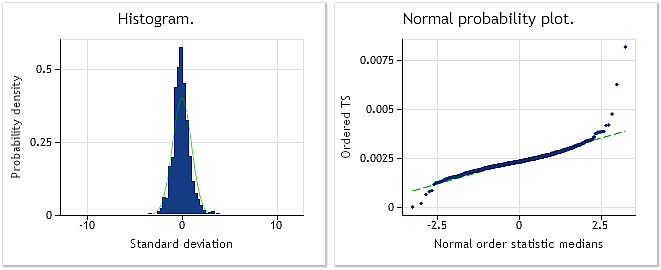
图 9. EURUSD M1 增量。Jarque-Bera 测试 JB=32494.8、p=0.000
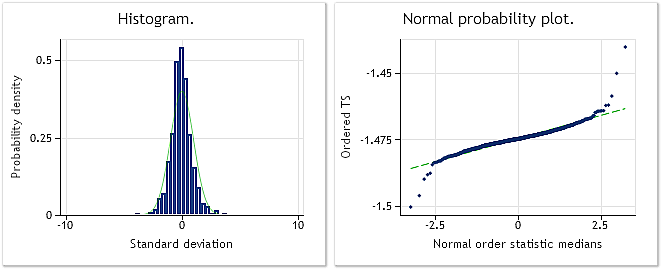
图 10. 变换序列。Lambda 参数=0.6662,Jarque-Bera 测试 JB=10302.5、p=0.000
图 9 显示 EURUSD M1 增量(差值)序列的特性,图 10 显示经 Box-Cox 变换后所获序列的特性。尽管 Jarque-Bera 测试值在变换后下降到不足原来的三分之一,从 JB = 32494.8 至 JB = 10302.5,变换序列的分布规律仍远非正态。
然而,我们不应该草率地作出结论,认为 Box-Cox 变换无法恰当处理增量变换。我们仅仅考虑了一个特例。使用其他输入序列,我们也许会得到大相庭径的结果。
此前引用的所有 Box-Cox 变换示例涉及的情形是,原始序列的分布规律应该是正态的或分布规律尽可能接近正态分布。在本文一开始即已提到,这种变换在使用参数化分析方法时是必要的,因参数化分析方法对所考察序列的分布规律相较正态分布的偏离十分敏感。
给出的示例表明,在变换后的所有情形中,根据 Jarque-Bera 测试结果,我们获得的序列相较原始序列其分布规律更接近于正态分布。这一事实清楚地表明 Box-Cox 变换的通用性和效率。
但是,我们不应过高估计 Box-Cox 变换的可能性,认为任意输入序列都将变换为严格的正态序列。从上面的示例可以看出,这是不现实的。无论是原始序列,还是变换序列,都不能视为实际报价的正态序列。
到目前为止,我们仅讨论了 Box-Cox 变换较为直观的一个参数的形式。这样做是为了降低第一次接触的难度。此方法证明了这种变换的能力,但对于实际运用,最好使用它的通用表现形式。
应当指出,Box-Cox 变换仅适用于具有正值和非零值的序列。在实际应用中,这一要求很容易通过将序列简单地向正区移位而得到满足,但是,在正区内的移位幅度可直接影响变换结果。
因此,我们可以将移位值视为额外的变换参数,将其随 lambda 参数一起进行最优化,防止序列值进入负区。
对于长度为 N 的原始序列 X:
![]()
确定两位参数 Box-Cox 变换的更通用形式的表达式如下所示:
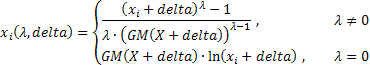
其中:
![]() ;
;
GM() - 几何平均值。
序列的几何平均值可通过以下方法计算:
![]()
我们可以看到,两个参数已经用于显示的表达式中 - lambda 和 delta。现在,我们需要在变换过程中同时优化这两个参数。尽管算法有一点复杂,但引入额外的参数无疑会提高变换的效率。此外,相比之前使用的变换,额外的正态化因数出现在表达式中。有了这个因数,变换结果将在 lambda 参数的变化过程中保持其范围。
有关 Box-Cox 变换的更多信息,请参考 [7]、[8]。一些相同类型的其他变换在 [8] 中作了简要说明。
下面是目前更通用的变换形式的主要特征:
在此前引用的所有示例中,对数似然函数标准被用于搜索 lambda 参数最优值。当然,这并不是估算变换参数的最优值的唯一方法。
我们可以将参数的最优化方法作为一个示例提及,该方法基于对按升序排序的变换序列和正态分布序列的函数分位数之间的相关系数的最大值的搜索。此情形已在前文中述及。正态分布函数分位数的值可根据 James J. Filliben 提出的表达式计算 [9]。
确定两位参数变换的通用形式的表达式无疑比我们之前讨论的表达式更为复杂。也许,这就是这种类型的变换很少用于数学和统计软件包的原因。引述的表达式已在 MQL5 中实现,可在必要时提供使用更为通用形式的 Box-Cox 变换的可能性。
CFullBoxCox.mqh 文件包含 CFullBoxCox 类的源代码,此类用于执行变换参数的最优值搜索。正如此前已提及的,最优化过程基于相关系数的计算。
//+------------------------------------------------------------------+ //| CFullBoxCox.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //+------------------------------------------------------------------+ //| CFullBoxCox class | //+------------------------------------------------------------------+ class CFullBoxCox:public PowellsMethod { protected: int Dlen; // data size double Dat[]; // input data array double Shift[]; // input data array with the shift double BCDat[]; // transformed data (Box-Cox) double Mean; // transformed data average value double Cdf[]; // Quantile of the distribution cumulative function double Scdf; // Square root of summ of Quantile^2 double R; // correlation coefficient double DeltaMin; // Delta minimum value double DeltaMax; // Delta maximum value double Par[2]; // parameters array public: void CFullBoxCox(void) { } void CalcPar(double &dat[]); double GetPar(int n) { return(Par[n]); } private: double ndtri(double y0); // the function opposite to the normal distribution function virtual double func(const double &p[]); }; //+------------------------------------------------------------------+ //| CalcPar | //+------------------------------------------------------------------+ void CFullBoxCox::CalcPar(double &dat[]) { int i; double a,max,min; Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayResize(Shift,Dlen); ArrayResize(BCDat,Dlen); ArrayResize(Cdf,Dlen); //--- copy the input data array ArrayCopy(Dat,dat); Scdf=0; a=MathPow(0.5,1.0/Dlen); Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1]; Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0]; a=Dlen+0.365; for(i=1;i<(Dlen-1);i++) { //--- calculation of the distribution cumulative function Quantile Cdf[i]=ndtri((i+0.6825)/a); //--- calculation of the sum of Quantile^2 Scdf+=Cdf[i]*Cdf[i]; } //--- square root of the sum of Quantile^2 Scdf=MathSqrt(Scdf); min=dat[0]; max=min; for(i=0;i<Dlen;i++) { //--- copy the input data a=dat[i]; Dat[i]=a; if(min>a)min=a; if(max<a)max=a; } //--- Delta minimum value DeltaMin=1e-5-min; //--- Delta maximum value DeltaMax=(max-min)*200-min; //--- Lambda initial value Par[0]=1.0; //--- Delta initial value Par[1]=(max-min)/2-min; //--- optimization using Powell method Optimize(Par); } //+------------------------------------------------------------------+ //| func | //+------------------------------------------------------------------+ double CFullBoxCox::func(const double &p[]) { int i; double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret; lam=p[0]; del=p[1]; k1=0; k2=0; if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;} // Lambda > 5.0 else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;} // Lambda < -5.0 if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;} // Delta > DeltaMax else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin gm=0; for(i=0;i<Dlen;i++) { Shift[i]=Dat[i]+del; gm+=MathLog(Shift[i]); } //--- geometric mean gm=MathExp(gm/Dlen); gmpow=lam*MathPow(gm,lam-1); mean=0; //--- Lambda != 0.0 if(lam!=0) { for(i=0;i<Dlen;i++) { a=(MathPow(Shift[i],lam)-1.0)/gmpow; //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } //--- Lambda == 0.0 else { for(i=0;i<Dlen;i++) { a=gm*MathLog(Shift[i]); //--- transformed data (Box-Cox) BCDat[i]=a; //--- average value mean+=a; } } mean=mean/Dlen; //--- sorting of the transformed data array ArraySort(BCDat); a=0; b=0; for(i=0;i<Dlen;i++) { c=(BCDat[i]-mean); a+=Cdf[i]*c; b+=c*c; } //--- correlation coefficient ret=a/(Scdf*MathSqrt(b)); return(k1+k2-ret); } //+------------------------------------------------------------------+ //| The function opposite to the normal distribution function | //| Prototype: | //| Cephes Math Library Release 2.8: June, 2000 | //| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier | //+------------------------------------------------------------------+ double CFullBoxCox::ndtri(double y0) { static double s2pi =2.50662827463100050242E0; // sqrt(2pi) static double P0[5]={-5.99633501014107895267E1, 9.80010754185999661536E1, -5.66762857469070293439E1, 1.39312609387279679503E1, -1.23916583867381258016E0}; static double Q0[8]={ 1.95448858338141759834E0, 4.67627912898881538453E0, 8.63602421390890590575E1, -2.25462687854119370527E2, 2.00260212380060660359E2, -8.20372256168333339912E1, 1.59056225126211695515E1, -1.18331621121330003142E0}; static double P1[9]={ 4.05544892305962419923E0, 3.15251094599893866154E1, 5.71628192246421288162E1, 4.40805073893200834700E1, 1.46849561928858024014E1, 2.18663306850790267539E0, -1.40256079171354495875E-1,-3.50424626827848203418E-2, -8.57456785154685413611E-4}; static double Q1[8]={ 1.57799883256466749731E1, 4.53907635128879210584E1, 4.13172038254672030440E1, 1.50425385692907503408E1, 2.50464946208309415979E0, -1.42182922854787788574E-1, -3.80806407691578277194E-2,-9.33259480895457427372E-4}; static double P2[9]={ 3.23774891776946035970E0, 6.91522889068984211695E0, 3.93881025292474443415E0, 1.33303460815807542389E0, 2.01485389549179081538E-1, 1.23716634817820021358E-2, 3.01581553508235416007E-4, 2.65806974686737550832E-6, 6.23974539184983293730E-9}; static double Q2[8]={ 6.02427039364742014255E0, 3.67983563856160859403E0, 1.37702099489081330271E0, 2.16236993594496635890E-1, 1.34204006088543189037E-2, 3.28014464682127739104E-4, 2.89247864745380683936E-6, 6.79019408009981274425E-9}; double x,y,z,y2,x0,x1,a,b; int i,code; if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);} if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);} code=1; y=y0; if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;} // 0.135... = exp(-2) if(y>0.13533528323661269189) // 0.135... = exp(-2) { y=y-0.5; y2=y*y; a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i]; b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i]; x=y+y*(y2*a/b); x=x*s2pi; return(x); } x=MathSqrt(-2.0*MathLog(y)); x0=x-MathLog(x)/x; z=1.0/x; //--- y > exp(-32) = 1.2664165549e-14 if(x<8.0) { a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i]; b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i]; x1=z*a/b; } else { a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i]; b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i]; x1=z*a/b; } x=x0-x1; if(code!=0)x=-x; return(x); } //------------------------------------------------------------------------------------
在最优化过程中,变换参数的变化范围存在一些限制。Lambda 参数值限制为 -5.0 到 5.0。Delta 参数的限制相对于输入序列的最小值指定。此参数通过 DeltaMin=(0.00001-min) 和 DeltaMax=(max-min)*200-min 值进行限制,其中 min 和 max 是输入序列元素的最小值和最大值。
FullBoxCoxTest.mq5 脚本展示了 CFullBoxCox 类的使用。此脚本的源代码显示如下。
//+------------------------------------------------------------------+ //| FullBoxCoxTest.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CFullBoxCox.mqh" CFullBoxCox Bc; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double dat[],shift[],bcdat[],lambda,delta,gm,gmpow; string fname; //--- input file name fname="Dataset2\\EURUSD_M1_1200.txt"; //--- reading the data if(readCSV(fname,dat)<0){Print("Error."); return;} //--- data size n=ArraySize(dat); //--- shifted input data array ArrayResize(shift,n); //--- transformed data array ArrayResize(bcdat,n); //--- lambda and delta parameters optimization Bc.CalcPar(dat); lambda=Bc.GetPar(0); delta=Bc.GetPar(1); PrintFormat("Iterations= %i, lambda= %.4f, delta= %.4f", Bc.GetIter(),lambda,delta); gm=0; for(i=0;i<n;i++) { shift[i]=dat[i]+delta; gm+=MathLog(shift[i]); } //--- geometric mean gm=MathExp(gm/n); gmpow=lambda*MathPow(gm,lambda-1); if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;} else {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);} //--- dat[] <-- input data //--- shift[] <-- input data with the shift //--- bcdat[] <-- transformed data } //+------------------------------------------------------------------+ //| readCSV | //+------------------------------------------------------------------+ int readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------
在脚本的开头,输入序列从文件上传至 dat[] 数组,然后变换参数的最优值搜索执行。接下来,程序使用获得的参数执行变换本身。结果,dat[] 数组包含原始序列,shift[] 数组包含按 delta 值移位的原始序列,bcdat[] 数组包含 Box-Cox 变换的结果。
Box-Cox-Tranformation_MQL5.zip 档案中包含了 FullBoxCoxTest.mq5 脚本编译所需的全部文件。
我们使用的测试序列的变换通过 FullBoxCoxTest.mq5 脚本执行。正如已经预期的那样,在对获得数据的分析过程中,我们可以得出结论:相比一个参数的类型,两参数变换类型得出的结果更优。例如,对于分析结果在图 6 中显示的 EURUSD M1 序列,Jarque-Bera 测试值 JB=100.94。在一参数变换后 JB=39.30(请参见图 7),而在两参数变换后(FullBoxCoxTest.mq5 脚本),此值降至 JB=37.49。
本文探讨了在 Box-Cox 变换的参数取得最优值时结果序列的分布规律尽可能地接近于正态分布规律的情形。但在实践中也会出现以稍微不同的方式使用 Box-Cox 变换的情形。例如,在预测时间序列时可以使用下述算法:
在上述算法中,通过预测误差最小化标准最小化变换参数和预测模型。在这种情况下,Box-Cox 变换的目标不再是将输入序列变换为正态分布定律。
现在,必须变换输入序列以得到具有最小预测误差的分布规律。取决于选择的预测方法,此分布规律不一定要是正态的。
Box-Cox 变换仅适用于由正值和非零值组成的序列。在其他所有情形中都应执行输入序列的移位。变换的这一特征当然可称之为它的缺点之一。但即便如此,Box-Cox 变换仍然是其他同类变换中最通用和有效的工具。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
