简介

我们在实践中必须处理的所有真实过程都很复杂，作为一项原则，包含大量的分量。例如天气。在分析降水图时，我们应记住，它们表示各种各样的过程的互动，例如季节变换、全球变暖/变冷过程、洋流变化、气旋和反气旋的动态、排放到大气中的二氧化碳的量、太阳活动周期等，内容不胜枚举。

因此很难分析此类图，因为其分量在相互作用时会遮挡我们要识别的规律或让规律扭曲。这样会让人有理由出现将考虑的过程分解为单个分量并单独分析每个分量的想法。分析单个分量并研究它们已经为当前过程做出的贡献有助于我们更好地了解正在进行的过程，并提高预测可靠性。

在讨论有关交易的各种信息时也不例外，包括依据大量不同因素形成的货币报价。这是很自然地期待预先分解为单个分量能够大大促进它们的进一步分析的原因。

术语“分解”在形式上指将一个复合过程或复合材料分解为单独的组成部分。但是在与不同过程分析、信号分析、各种序列分析有关的很多领域中，此术语长期以来具有更为广阔的含义，通常不是指分解为实际的初始组成部分，而是指分解为在形成初始数据时实际上并不存在的某些函数。这些函数是在数据分解过程中人工形成的，但是尽管它们是“人工”的，它们也能更加深入地分析数据，有助于识别隐藏的形态。

在市场分析中使用的大量方法或明或暗都可归于从分析过程中挑选某些分量的方法，即分解法。让我们简要地回顾一下这些方法。

1. 分解

在实践中，有很多各种各样的分解法可应用到考虑的给定序列。这些方法可能有不同的基本数学或经验方法，不同的复杂程度和不同的应用领域。

例如，即使一个基本市场分析在一定程度上也可被视为一种分解法。此分析处理一组直接影响市场状况的初始事件产生的影响。换言之，所分析的市场过程被暗中分解为若干组成该过程的事件。

以后将不触及与基本分析有关的问题。我们假定有关过程的任何进一步的信息都不可用；我们拥有的仅是表示给定过程的行为的一个序列。

可以用常见的方法将一个序列分解为几个组成部分，以之说明最简单的分解例子。例如，我们为任意货币对在图表上标绘移动平均线 (MA)。然后从初始序列中减去生成的曲线。这样一来，我们将得到初始序列的两个组成部分，MA 曲线和残数。相同的步骤，仅使用较长周期的移动平均线，在应用到获得的残数时，将产生三个组成部分 - 两条 MA 曲线和变换的残数。如您所见，可以使用任何可用的方式安排分解过程。要点在于此类过程的结果的属性。

在著名的分解和频谱分析方法中，傅里叶变换特别值得在这里提及。傅里叶变换属于使用固定谐波基函数的正交变换类。傅里叶变换结果可表示为初始过程分解为具有固定频率和幅度的谐函数。注意，有两点对我们特别重要。

第一点，变换始终依据一个固定的、预先设定的正交函数基进行。即变换基不取决于所变换的序列的性质。

第二点，生成的谐分量的幅度和频率值是恒定的。即它们的值在整个初始序列中都保持不变。这意味着如果给定初始序列的性质在所考虑的区间内出现变化，则这种变化将不会在变换结果中反映出来。在此情况下，获得的结果将仅反映过程的某个平均状态，因为此变换依据初始数据的静态假设。

为了避免与初始序列的非静态性有关的约束，我们可以将傅里叶变换转换为小波变换。小波变换，与傅里叶变换类似，以固定的函数基进行分解。与傅里叶变换不同，此基是预设的，即应选择在变换中使用的小波。

此外，与傅里叶变换相比，从小波变换生成的每一个分量都有确定其随时间而变换的比例和水平的参数，这样解决了与所分析的过程可能具有的非静态性有关的问题。

傅里叶变换和小波变换都被广泛认可，因为使用充分建立的数学技能和可用的有效实施算法。此外，两种变换都似乎特别通用，能够成功应用于不同的领域。

但是出于实践目的，最好使用不仅能够处理非静态过程，还能使用按初始数据确定的自适应变换基的变换。此类变换确实存在，以下将对其进行简要介绍，从而说明本文的主题。

2. 经验模态分解

经验模态分解 (EMD) 作为 希尔伯特-黄变换 (HHT) 的基础部分被提出来。可以这么说，希尔伯特-黄变换分为两个阶段进行。首先，使用 EMD 算法获得本质模态函数 (IMF)。

接着，在第二阶段，通过对上一步获得的结果应用希尔伯特-黄变换得到初始序列的瞬时频率谱。HHT 能够获得非线性和非静态序列的瞬时频率谱。之后，可以使用经验模态分解处理这些序列。

然而，本文将不介绍使用希尔伯特变换标绘瞬时频率谱。我们将仅着重于 EMD 算法。

与前面提及的傅里叶变换和小波变换相比，EMD 将任何给定数据分解为本质模态函数 (IMF)，这些函数在分析上未被设定，而是由所分析的序列单独确定。在这种情况下，基函数从输入数据自适应地直接得出。从 EMD 生成的 IMF 应满足以下要求：

1. IMF 极值的数量（最大值和最小值的数量之和）与零穿越的数量必须相等或最多相差 1；
2. 在 IMF 的任意点，局部最大值定义的包络线的平均值和局部最小值定义的包络线的平均值应等于零。

分解生成一系列的频率分阶 IMF 分量。每个后面的 IMF 包含比前面的 IMF 更小的频率振荡。尽管“频率”这一术语在运用到 IMF 时并不十分正确，但它可能最适合用于定义 IMF 的性质。本质在于尽管 IMF 是振荡性质，但其幅度和频率可以沿时间轴变化。

单独依据描述对 EMD 算法执行结果进行可视化非常困难，因此让我们继续其软件实施，这样让我们有机会了解算法的特点。

3. EMD 算法

黄锷 (Norden E. Huang)提出的算法以产生序列的局部最大值和最小值所定义的平滑包络线，接着从初始序列减去这些包络线的平均值为基础。这要求识别所有局部极值，然后用三次样条曲线进一步将这些极值连接起来，以生成上下包络线。

标绘包络线的过程如图 1 所示：

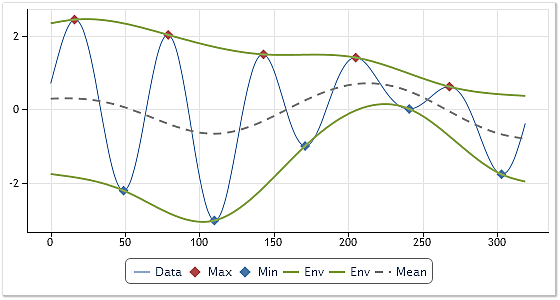
图 1. 描绘包络线和它们的平均值

图 1 用细蓝线给出了所分析的序列。分别用红色和蓝色表示序列的最大值和最小值。用绿色给出包络线。

依据两条包络线计算平均值，并在图 1 中以虚线表示。从初始序列中进一步减去这样计算出来的平均值。

以上步骤生成所需经验函数的首次逼近提取。为了获得最终的 IMF，应再次识别新的最大值和最小值并重复以上所有步骤。此次重复的过程称为筛选。重复筛选过程，直到满足某个给定的停止标准。筛选停止标准的选择是影响最终分解结果的要点之一。我们将在迟些时候讨论这个问题。

如果成功完成筛选过程，则我们将获得第一个 IMF。可以通过从原始信号减去先前提取的 IMF，再一次重复上述过程而获得下一 IMF。这样一直继续到提取完所有 IMF 为止。筛选过程通常在残数只包含不超过两个极值时停止。

可以看到，描述的经验模态分解过程并不是基于严格的数学计算，但是真正基于经验，正如其名。尽管黄锷提出的以上算法简单明了，仍然有几点可被视为其弱点。

有关此主题的不同文章提供了对其弱点的详细说明，以及对黄锷的算法进行现代改进的方式。本文将不着重于对此方法进行的可能现代改进，但是将简单地说明创建其软件实施的尝试。以下简单地介绍实施的特征。

4. CEMDecomp 类

实施 EMD 算法的 CEMDecomp 类是依据研究希尔伯特-黄变换和经验模态分解的互联网文章创建的。实施的算法在本质上与黄锷最初提出的算法非常类似，没有包含任何重大修改。

以下是源代码的一个片断，可以在本文末尾的 CEMDecomp.mqh 文件中找到。

//------------------------------------------------------------------------------------
// The Empirical Mode Decomposition (EMD).
//------------------------------------------------------------------------------------
class CEMDecomp:public CObject
  {
public:
  int     N;                 // Input and output data size
  double  Mean;              // Mean of input data
  int     nIMF;              // IMF counter
  int     MaxIMF;            // Maximum number of IMF
  int     MaxIter;           // Maximum number of iterations
  int     FixedIter;         // 0-variable number of sifting iterations;
                             // 1-always ten sifting iterations.
  double  IMFResult[];       // Result
private:
  double  X[];
  double  Imf[];
  double  XMax[];            // x of local maxima
  double  YMax[];            // y of local maxima
  double  XMin[];            // x of local minima
  double  YMin[];            // y of local minima
  double  EnvUpp[];          // Upper envelope
  double  EnvLow[];          // Lower envelope
  double  Eps;               // Accuracy comparison of floating-point numbers
  double  Tol;               // Accuracy of calculation IMF
public:  
  void    CEMDecomp(void);
  int     Decomp(double &y[]);          // Decomposition
  void    GetIMF(double &x[], int nn);  // Get IMF number nn
private:
  int     arrayprepare(void);
  void    extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]);
  int     SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0);
  };

让我们看一看在 CEMDecomp 类中声明的公共变量和方法。

N 是序列中元素的数量。变量 N 的值在调用 Decomp() 方法之后生成，等于输入序列的长度。提取的 IMF 将具有相同的大小。

Mean 是输入序列的平均值。值在调用 Decomp() 方法之后生成。

nIMF 是 IMF 计数器。在调用 Decomp() 之后，它包含提取的 IMF 的数量加 2。因此，这个值指出使用 GetIMF() 方法可以读取多少分量。这就是说，索引为 0 的分量将始终包含从中减去其平均值的初始序列，索引为 nIMF 的分量将包含分解的残数。

MaxIMF 是 IMF 的最大允许数量。当 IMF 的数量达到 MaxIMF 值时，输入序列分解为单个的 IMF 将停止。此变量的值可在调用 Decomp() 方法之前设置。默认值为 16。

MaxIter 是在筛选过程中允许的最大迭代次数。如果筛选过程的迭代次数达到此值，则不管是否获得需要的精确度，筛选都会停止。此变量的值可在调用 Decomp() 方法之前设置。默认值为 2000。

FixedIter 是一个标记，在筛选中设置一个停止标准。如果 FixedIter 的值为零，则在达到给定精确度时，每个 IMF 的筛选过程就会停止。对不同 IMF 的提取而言，实现给定精确度所需的迭代次数可能有所不同。如果 FixedIter 设置为 1，则 IMF 会在 10 次迭代内被提取出来。此变量的值可在调用 Decomp() 方法之前设置。默认值为 0。

Decomp(double &y[]) 是主要的类方法，执行分解。它以输入参数的形式接收到一个包含输入数据的数组的引用 。在成功完成时，变量 N 将等于输入数组的长度。提取的 IMF 将具有相同的大小。变量 Mean 将等于输入序列的平均值，变量 nIMF 将等于可用 GetIMF() 方法读取的分量的数量。

GetIMF(double &x[], int nn) 用于确保访问用 Decomp() 方法获得的结果。用 nn 设定数量的分量，这些分量会被复制到数组，而数组的地址会作为一个输入参数传递。这就是说，索引为 0 的分量将始终包含从中减去其平均值的初始序列，索引为 nIMF 的分量将包含分解的残数。如果作为参数传递的数组长度小于生成的分量的长度，则会按数组长度允许的情况填充数组。

可以用以下例子来说明 CEMDecomp 类的使用：

#include "CEMDecomp.mqh"
//------------------------------------------------------------------------------------
// Script program start function
//------------------------------------------------------------------------------------
void OnStart()
  {
  int n,ret;
  double yy[],imf2[];
  
  n=400;                                    // Input sequence length
  ArrayResize(yy,n);                         // Array of input data
  ArrayResize(imf2,n);                       // Array for reading the results
  
  CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy);      // Generation of input data
  
  CEMDecomp *emd=new CEMDecomp();           // Creation of the CEMDecomp class instance
  ret=emd.Decomp(yy);                       // Decomposition of the input sequence
  
  if((ret==0)&&(emd.nIMF>3))                // If there is no error and the sufficient
                                            // number of components was extracted,
    emd.GetIMF(imf2,2);                     // copy component number 2 into
                                            // array imf2[].
  delete(emd);                              // Deletion of the CEMDecomp class instance
  
  // One of the extracted components in array imf2[].
  }
//------------------------------------------------------------------------------------

可以在本文末尾的 CEMDecomposition.zip 压缩文件中找到通过 Web 界面显示提取的 IMF 的完整分解例子。为了运行这个例子，应解压缩指定的压缩文件，并将整个 \CEMDecomposition 目录及其内容放在客户端的 \Indicators 或 \Scripts 目录内。之后，您可以编译并运行 EMDecomp_Test.mq5 脚本。请记住，应允许在客户端中使用外部库。

图 2 显示另一个例子，使用 USDJPY 每日报价的分解，序列长度为 100 个元素。可以看到，此序列的分解生成四个 IMF 提取和残数。

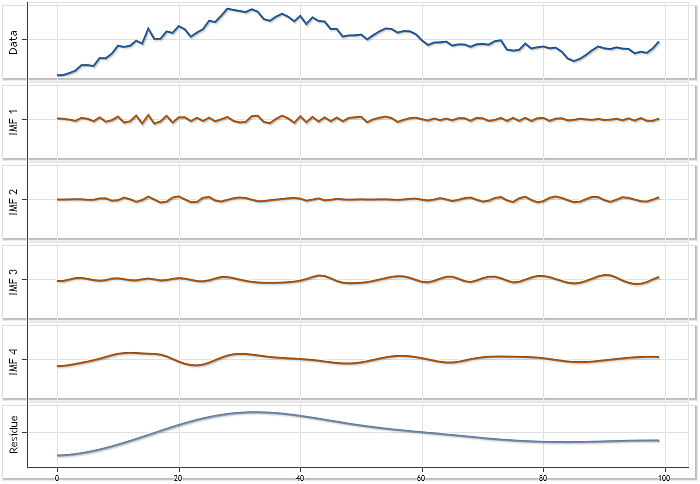
图 2. USDJPY 每日报价序列的分解，其中 N=100

图 2 中的所有图表都以相同的刻度显示，这样能够评估每个提取的 IMF 做出的贡献。然而，这种绘图方式不能提供足够的清晰画面来查看每个 IMF 的特性。图 3 说明了相同的结果，但是对每个图表使用自动缩放模式。

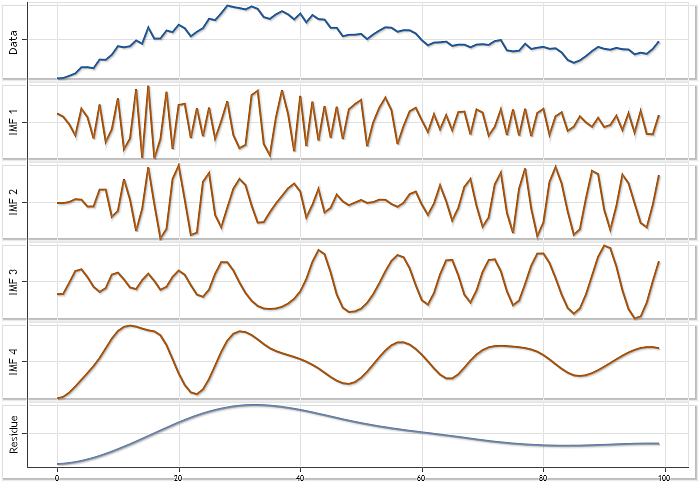
图 3. USDJPY 每日报价序列的分解，其中 N=100。自动缩放模式

尽管图 3 没有显示单个分量的幅度的实际相关性，使用自动缩放模式能够对每一个图表进行更加详细的可视化。

5. 有关所提议 EMD 算法实施的说明

我要提醒您注意的第一样东西是用于识别初始序列的最大值和最小值的方法。在这个例子中，有两个选项可用。

图 4 显示极值识别算法的执行结果。

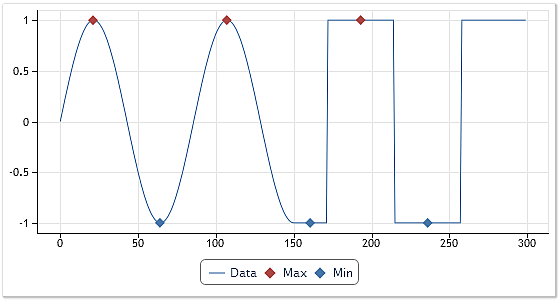
图 4. 极值的识别。第一个选项。

在要识别函数的最大值和最小值时，最常用的算法如下：

1. 将序列的当前元素的值与前面和后面的值进行比较；
2. 如果当前值大于前面的值和后面的值，则将其确定为函数的最大值；
3. 如果当前值小于前面的值和后面的值，则将其确定为函数的最小值；

如果具有明显定义极值的序列，最大值和最小值的识别没有任何困难。提供的算法运行得非常好。图 4 中图表的前一半说明了这种情形。然而，在序列的最接近的值相等的顶部，此算法就反应迟钝了。

使用提供的算法，绝对不会识别出图 4 中的最后一个最大值和最后两个最小值。一方面，此结果是期待中的正确结果。但是另一方面，如果出现零穿越，在绘制振荡过程的类推时，这些极值会被忽略。矩形序列的顶部或者相等序列值的区段是否能被视为极值尚不清楚。

尽管如此，在实施 EMDecomp 类时用于识别极值的算法是以上算法的改进版。可以在图 4 中观察到其执行结果。此算法将具有相等序列值的区间识别为极值，并将极值点放在这些区间的中央。

用于识别最大值和最小值的算法，其执行结果显示在图 4 中，在确定分解循环应停止的点时，在 CEMDecomp 类中用于计算极值的数量。举例而言，如果提取的 IMF没有任何极值，则分解停止，并且此类 IMF 被抛弃。

如果在描绘包络线时使用此识别算法，则举例而言，在输入序列采用如图 4 所示的形式时，生成的包络线会是两条平行的直线。筛选过程因而将无法变换输入序列，而这个输入序列将不适合分解为分量。

使用稍有区别的极值识别算法以描绘包络线可解决这个问题。

图 5 说明使用备选的极值识别算法得到的结果。

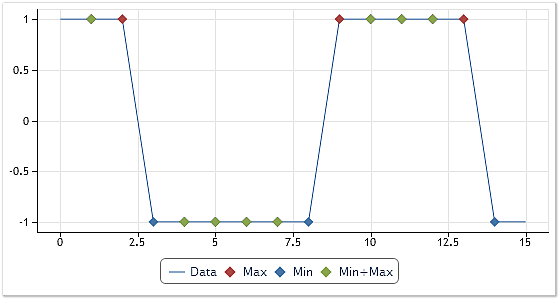
图 5. 极值的识别。第二个选项。

让我们仔细观察图 5。与图 4 不同，它以绿色显示既是最大值又是最小值的点。如果基于这些极值描绘包络线，则它们将不再是平行的直线，并且矩形序列的隐藏分量将可用于在筛选过程中进一步提取。位于本文末尾的 CEMDecomposition.zip 压缩文件中的一个测试案例能够很好地说明以上情形。

很不幸，此方法不能解决与隐藏分量的提取有关的所有问题。例如，对于三角形序列，不能用这种方式提取隐藏分量。这一事实是这种 EMD 算法实施的弱点之一。或许可以通过切换到 CEEMD（Complementary Ensemble Empirical Mode Decomposition Method，补余经验模态分解法) 分解算法来解决这个困难；本文并不介绍该算法。

除了与极值识别算法实施有关的特性以外，还应注意此类算法通常具有的末端影响问题。为了详细说明以上情形，让我们转到图 1。图 1 清晰地表明最大值被一个三次插值样条函数连接，作为上包络线。

这就是说，应为第一个最大值的左侧区段和最后一个最大值的右侧区段定义包络线。延长此包络线的方式类似于确定在其末尾附近提取的 IMF 的性质。本文不对末端影响修正的软件实施进行详细说明，只是简单地在这里指出这一事实，引起读者的注意。

我们应进一步指出，提取的 IMF 的性质和数量能够并且将取决于为停止筛选循环而选择的方法。CEMDecomp 类使用表示当前 IMF 中的差异程度的比值（由最后一个筛选循环确定）的计算作为用于停止筛选过程的主要方法。

如果筛选对一个未知 IMF 几乎没有作用，则筛选过程停止，并且 IMF 被视为已经生成。默认情况下，在类的构造函数中设置一个用于确定 IMF 提取精确度的极限值。设置默认的极限值之后，筛选迭代次数有时可达到 200 甚至 300.在有关此主题的文章中，很多作者对使用如此之大的筛选迭代次数提出了警告。尽管如此，还是决定在这种 EMD 算法实施中使用这个默认极限值。

这种 EMD 算法实施能够使用其他停止标准。为此，在调用 Decomp() 方法之前，应将变量 FixedIter 设置为 1。在这种情况下，所有 IMF 都将在 10 次筛选迭代内被提取出来。并且很容易看到，与默认方法相比，使用这个停止标准得到的分解结果有一点区别。

6. EMD 算法的应用

因为 EMD 算法最初是希尔伯特-黄变换的一部分，序列的瞬时频率谱计算可用作示范此算法的应用的一个例子。这涉及对使用 EMD 提取的 IMF 分量进行希尔伯特-黄变换。然而，本文并不介绍这个过程。

除了计算频率谱以外，EMD 算法还可用于平滑序列。

图 6 显示此类平滑的一个例子。

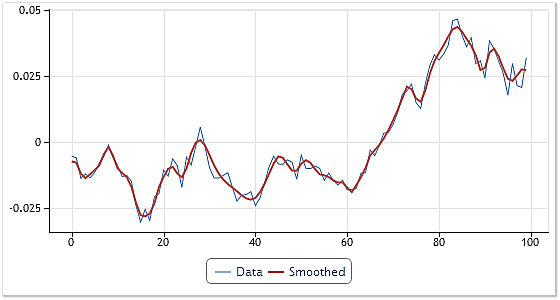
图 6. 输入序列的平滑

选择包含 100 个“开盘”价的任意 USDCHF 每日报价片断进行平滑。在分解过程中，得到四个 IMF 和残数。除了第一个以外，所有 IMF 被进一步添加到残数。

因此，找到的最高频率分量被排除在输入序列以外。如果我们在将它们加起来时放弃前两个分量，则生成的曲线将会更加平滑。

EMD 应用的另一个例子是基于从输入序列提取的 IMF 生成预测。要生成预测，可以使用任意外推器，借此为每个 IMF 和残数单独生成预测。

然后将用这种方式生成的预测加起来，为输入序列生成需要的预测结果。考虑到单个 IMF 的振荡性质，我们可以假定要生成预测，使用考虑了预测序列的周期行为的外推器应该是合理的。

在我们的情形中，我们将回顾一个更为简单的外推器的运行例子，其中使用 10 步前进线性外推生成每个 IMF 的预测。图 7 显示了此预测的结果。

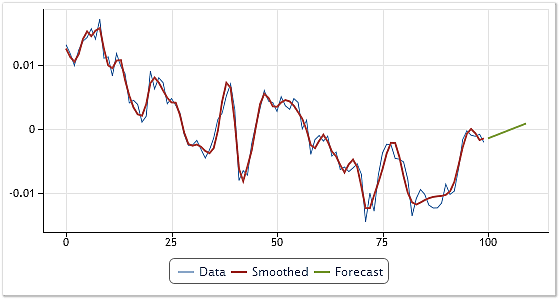
图 7. 为 USDCHF，H4 报价生成预测

应该指出，在生成预测时，可以放弃一个或多个最高频率的分量。因此，高频噪声对预测的影响可得到抑制。图 7 说明了排除第一个 IMF 的预测的结果。在本例中，没有评估这种方法的预测能力。在这里没有提供以经验模态分解为基础的预测方法的详细分析，因为这个主题不在本文的讨论范围之内。

我们也不得不提及趋势剔除。在使用 EMD 得到单个的序列分量之后，可以开发一个非常灵活的算法来进行趋势剔除。分解的残数或添加到一个或多个最后提取的 IMF 的残数可被当作一个趋势。创建趋势线所涉及的 IMF 以及残数的数量视在剔除趋势之后需要在序列中保留的低频分量的数量而有所不同。

因此，要剔除趋势，除了最后一个或几个分量以外，将所有作为分解的结果提取的 IMF 加在一起就足够了。此过程可以方便地与对获得的结果进行平滑结合在一起，如果已经从将分量加在一起的过程中排除了最高频率分量的话。图 8 显示了使用以上技术剔除趋势的例子。

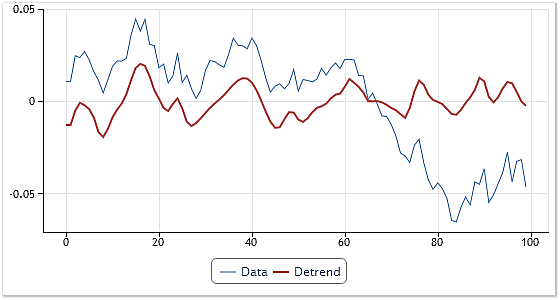
图 8. 与平滑结合在一起的趋势剔除

将 EURUSD 每日报价的一个序列作为初始数据。在分解之后，将所有提取的分量加在一起，但不包括分解的残数，第一个和最后一个 IMF。这样一来，不仅仅是剔除趋势，还对生成的曲线进行一定程度的平滑。

经验模态分解法的应用领域当然不限于本文给出的简单例子。但是因为本文更加专注于 EMD 方法的实施问题，而不是其应用，让我们考虑一下以下例子。

说明使用在 CEMDecomp.mqh 中设定的参数获得的分解结果的图 9 可作为这种 EMD 方法实施的另一个功能说明。这个例子以使用 XAUUSD H4 报价为基础。序列长度为 150 个元素。

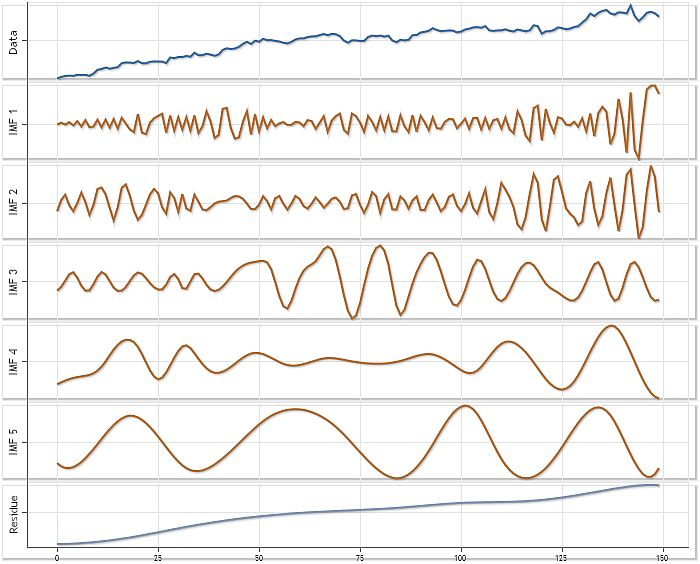
图 9. 使用 XAUUSD H4 报价的分解例子

在图 9 中，对每个分量应用了自动缩放。

总结

记住，经验模态分解法以及希尔伯特-黄变换用于分析非静态和非线性过程产生的数据。这并不意味着此方法不能应用到线性和静态序列。

本文的开头简单提及了在分解算法中使用的几个方法。并且指出这些算法中的大部分将一个序列分解为若干分量，这些分量事实上并不代表实际构成所考虑的序列的初始过程。

这些分量是以某种形式合成的；它们的提取仅帮助更好地了解输入序列的结构，并且在很多情形中能够促进其分析。EMD 方法也不是例外。您绝对不应该认为使用此方法获得的分量反映了最初从中形成初始分析数据的实际物理过程。

本文提出的实施可能需要进一步测试和改进，因为很难将其视为一个理想的实施。

然而，本文的主要目的是让读者熟悉 EMD 方法以及与其实施有关的某些特点。

总结如下：

1. 本文非常简要地介绍某些一般性的分解相关问题；
2. 简单而言，它指出了经验模态分解法的本质；
3. 介绍了在其中实施 EMD 方法的 CEMDecomp 类接口的列表和简短说明；
4. 给出了与 CEMDecomp 类进行互动的例子，也说明了如何调用其方法；
5. 大概介绍了所提 EMD 方法实施的某些特点；
6. 提供了几个例子，说明 EMD 方法在数据分析中的应用；
7. 在本文的末尾，您可以找到实施 EMD 方法的 CEMDecomp.mqh 文件，以及 EMDecomposition.zip 压缩文件，该文件包含介绍 CEMDecomp 类的使用的完整测试案例。

参考文献

1. 希尔伯特-黄变换。
2. 希尔伯特-黄变换。
3. 经验模态分解。

附录

原文发表于 2012 年 6 月 28 日。本附录于 2012 年 7 月 5 日提供。

提供了另一个 EMD 方法实施作为本文的补充。该实施显示为 CEMD 类并包含在下面的附件 CEMD_2.mqh 中。