本篇内容用于研究组合优化方法对组合收益提升的影响,偏重于优化目标方法设置,标的选择均是权益类资产,用于全A股测试,同时考虑到研究的实际意义,我们设置行业资产配置这样的组合情境(同样也可以做不同板块配置优化),基于申万一级行业数据,采用了较为常见的最小方差、最大夏普、风险平价这样的模型,应用在行业配置中,来探索组合优化模型效果。
组合优化的目的在于给予高收益,低风险的标的更多的权重,来提高组合整体表现。策略里面大部分情况下都会默认平均持仓的方法,由于没有考虑各个标的风险的不同,标的之间的相关性,并未较好的解决鸡蛋在一个篮子里的问题,若是稍加关注一下对组合权重的处理,就会考虑到各标的间的涨跌是否本身就有较强关联这样的问题,这个时候就是需要研究各标的时间序列协方差、波动率等内容的时候。
接下来将28个申万一级行业指数进行研究,给予不同权重配置,首先,获取了行业指数数据,构造收益序列效果如下图所示
可以看到,各行业之间涨跌存在一定的差异
但在极端行情如2015年6月之前的牛市和之后的熊市都有着一致的表现
下面获取了行业间相关矩阵,并以热力图进行展示
热力图颜色又深到浅表示相关度有低到高的过程
从图中可以明显看到银行业与非银金融与其他行业有着较为明显的不同
化工、电器设备、机械设备、纺织服装等行业都有较高的相关度
开始之前,我们先对这些优化方法进行说明
1)平均分仓
就是对28个行业进行等权重资金配置
2)等波动率
等波动率是使得每个股票贡献的表征风险相等,如组合中第i个标的的权重为
满足如下条件:
4)风险平价
风险平价模型是通过衡量组合各标的对于组合的风险贡献度,来制定投资模型的各类资产权重,目标是使得组合标的达到等风险贡献
此优化方法下的行业配置权重
5)最大夏普
夏普率用来表示每承受一单位风险,会产生多少的超额报酬,是对策略的收益与风险进行综合考虑
目标函数为追求最大
即寻找目标
此优化方法下的行业配置权重
以下是不同组合优化的净值表现
我们调用scipy.optimize提供的优化算法,构造以上的目标函数,进行优化求解。
模型模拟了季度调仓,保存调仓时点计算出的权重结构,构造回测,并计算相应风险指标,得出如下结果
以下结论是基于对近5年申万行业指数时间序列不同组合优化方法得出
(1)组合优化处理后普遍优于平均分仓的效果
(2)最小方差组合效果显著,累计收益从39.2%提升至76.9%,年化收益从7.98%提升至12.85%,最大回撤从56.46%降低至40.51%,夏普比率从0.12提升至0.41
(3)最大夏普模型表现最差,且模型持股过于集中
(4)几种优化方法整体提升效果一般,区分度不够明显,如年化波动0.2467略微降低至0.2187,最大回撤仅从56.46%优化到47.87%
组合优化方法是分散化投资的理论工具,分散化投资降低风险,是寻找相关度低的资产作为投资标的,而A股市场标的基本都有着较高的贝塔值,这使得所有行业同样与大盘有着一致的牛熊,因此组合优化效果不尽如人意,基于组合优化方法,在更为宏观的市场领域内,选择相关度低的资产进行配置,这样的场景能更好的发挥组合优化模型的工具优势。
本篇内容用于研究组合优化方法对组合收益提升的影响,偏重于优化目标方法设置,标的选择均是权益类资产,用于全A股测试,同时考虑到研究的实际意义,我们设置行业资产配置这样的组合情境(同样也可以做不同板块配置优化),基于申万一级行业数据,采用了较为常见的最小方差、最大夏普、风险平价这样的模型,应用在行业配置中,来探索组合优化模型效果。 下面是结果展示
组合优化的目的在于给予高收益,低风险的标的更多的权重,来提高组合整体表现。策略里面大部分情况下都会默认平均持仓的方法,由于没有考虑各个标的风险的不同,标的之间的相关性,并未较好的解决鸡蛋在一个篮子里的问题,若是稍加关注一下对组合权重的处理,就会考虑到各标的间的涨跌是否本身就有较强关联这样的问题,这个时候就是需要研究各标的时间序列协方差、波动率等内容的时候。
接下来我们将28个申万一级行业指数进行研究,进行行业的不同权重配置,整个研究内容分布如下
以下结论是基于对近5年申万行业指数时间序列的不同组合优化方法得出
(1)组合优化处理后普遍优于平均分仓的效果
(2)最小方差组合效果显著,累计收益从39.2%提升至76.9%,年化收益从7.98%提升至12.85%,最大回撤从56.46%降低至40.51%,夏普比率从0.12提升至0.41
(3)最大夏普模型表现最差,且模型持股过于集中
(4)几种优化方法整体提升效果一般,区分度不够明显,如年化波动0.2467略微降低至0.2187,最大回撤仅从56.46%优化到47.87%
组合优化方法是分散化投资的理论工具,分散化投资降低风险,是寻找相关度低的资产作为投资标的,而A股市场标的基本都有着较高的贝塔值,这使得所有行业同样与大盘有着一致的牛熊,因此组合优化效果不尽如人意,基于组合优化方法,在更为宏观的市场领域内,选择相关度低的资产进行配置,这样的场景能更好的发挥组合优化模型的工具优势。
#导入需要的库
import pandas as pd
import numpy as np
from jqdata import jy
from jqdata import *
import seaborn as sns
import matplotlib as mpl
from cvxopt import solvers, matrix
import datetime as dt
from scipy.optimize import minimize
我们通过聚宽获取申万行业指数
为了统计近5年的行业配置组合优化效果,且考虑到需要一年的协方差数据,这里获取6年的行业指数准备数据
#获取所需的数据
s_date,e_date = '2012-11-10','2018-12-10'
moneyfund_price = get_price('511880.XSHG',start_date=s_date,end_date=e_date)
#通过聚源数据获取申万行业指数行情数据(输入行业指数代码)
def get_SW_index(SW_index = 801010,start_date = '2017-01-31',end_date = '2018-01-31'):
index_list = ['PrevClosePrice','OpenPrice','HighPrice','LowPrice','ClosePrice','TurnoverVolume','TurnoverValue','TurnoverDeals','ChangePCT','UpdateTime']
jydf = jy.run_query(query(jy.SecuMain).filter(jy.SecuMain.SecuCode==str(SW_index)))
link=jydf[jydf.SecuCode==str(SW_index)]
rows=jydf[jydf.SecuCode==str(SW_index)].index.tolist()
result=link['InnerCode'][rows]
df = jy.run_query(query(jy.QT_SYWGIndexQuote).filter(jy.QT_SYWGIndexQuote.InnerCode==str(result[0]), jy.QT_SYWGIndexQuote.TradingDay>=start_date, jy.QT_SYWGIndexQuote.TradingDay<=end_date
))
df.index = df['TradingDay']
df = df[index_list]
return df
hy_df = get_industries(name='sw_l1')
hy_price_dict = {}
for hy in hy_df.index[:]:
hy_price =get_SW_index(SW_index = hy,start_date = s_date,end_date = e_date)
hy_price_dict[hy] = hy_price['ClosePrice']
all_price_df = pd.concat(hy_price_dict.values(),axis=1)
all_price_df.columns = hy_df.index
#all_price_df['moneyfund'] = moneyfund_price['close']
all_price_df.head(5)
| 801010 | 801020 | 801030 | 801040 | 801050 | 801080 | 801110 | 801120 | 801130 | 801140 | ... | 801720 | 801730 | 801740 | 801750 | 801760 | 801770 | 801780 | 801790 | 801880 | 801890 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TradingDay | |||||||||||||||||||||
| 2012-11-12 | 1528.590 | 3962.991 | 1622.796 | 1741.893 | 3206.886 | 1176.792 | 1971.636 | 5427.914 | 1462.276 | 1261.643 | ... | 1541.14 | 2463.43 | 669.92 | 1394.66 | 415.09 | 1013.46 | 1904.07 | 954.65 | 2189.17 | 805.96 |
| 2012-11-13 | 1499.453 | 3884.033 | 1590.792 | 1726.088 | 3142.218 | 1155.724 | 1937.309 | 5348.192 | 1439.519 | 1237.030 | ... | 1516.85 | 2419.45 | 652.06 | 1376.12 | 408.56 | 995.20 | 1878.72 | 931.40 | 2144.75 | 789.38 |
| 2012-11-14 | 1497.408 | 3905.964 | 1593.432 | 1730.450 | 3190.026 | 1161.023 | 1946.278 | 5403.142 | 1440.246 | 1243.291 | ... | 1519.13 | 2427.09 | 650.20 | 1373.03 | 411.29 | 995.26 | 1881.99 | 937.51 | 2154.44 | 790.61 |
| 2012-11-15 | 1474.834 | 3825.147 | 1565.150 | 1706.524 | 3116.338 | 1134.229 | 1938.748 | 5330.755 | 1411.987 | 1219.751 | ... | 1498.51 | 2372.26 | 635.73 | 1351.85 | 402.49 | 971.07 | 1864.48 | 925.27 | 2113.20 | 776.73 |
| 2012-11-16 | 1463.087 | 3770.721 | 1556.309 | 1699.372 | 3082.460 | 1123.276 | 1926.942 | 5245.346 | 1403.346 | 1207.410 | ... | 1495.82 | 2359.95 | 628.49 | 1343.06 | 399.05 | 959.17 | 1855.31 | 917.71 | 2103.91 | 776.12 |
5 rows × 28 columns
绘制各行业指数时间序列走势图
mpl.pyplot.style.use('ggplot')
all_price_df.columns = list(hy_df['name'].values)#+['货币基金']
mpl.rcParams['font.family']='serif'
mpl.rcParams['axes.unicode_minus']=False # 处理负号
prices=all_price_df
(prices/prices.iloc[0]).plot(figsize=(18,12),grid='on')
pct_daily = prices.pct_change()
可以看到,各行业之间涨跌存在一定的差异
但在极端行情如2015年6月之前的牛市和之后的熊市都有着一致的表现
行业间相关性矩阵计算,并以热力图进行展示
#计算各行业指数相关矩阵
fig = plt.figure(figsize= (15,10))
ax = fig.add_subplot(111)
ax = sns.heatmap(pct_daily.corr(),annot=True,annot_kws={'size':9,'weight':'bold'})
热力图颜色又深到浅表示相关度有低到高的过程
从图中可以明显看到银行业与非银金融与其他行业有着较为明显的不同
化工、电器设备、机械设备、纺织服装等行业都有较高的相关度
(1)按季度调仓日期获取
我们设置季度调仓,进行组合风险平衡
#获取日期列表
#按月、季度、半年方式获取交易日列表
def get_tradeday_list(start,end,frequency=None,count=None):
if count != None:
df = get_price('000001.XSHG',end_date=end,count=count)
else:
df = get_price('000001.XSHG',start_date=start,end_date=end)
if frequency == None or frequency =='day':
return df.index
else:
df['year-month'] = [str(i)[0:7] for i in df.index]
if frequency == 'month':
return df.drop_duplicates('year-month').index
elif frequency == 'quarter':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='04') | (df['month']=='07') | (df['month']=='10') ]
return df.drop_duplicates('year-month').index
elif frequency =='halfyear':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='06')]
return df.drop_duplicates('year-month').index
get_tradeday_list(start=s_date,end=e_date,frequency="quarter",count=None)
DatetimeIndex(['2013-01-04', '2013-04-01', '2013-07-01', '2013-10-08',
'2014-01-02', '2014-04-01', '2014-07-01', '2014-10-08',
'2015-01-05', '2015-04-01', '2015-07-01', '2015-10-08',
'2016-01-04', '2016-04-01', '2016-07-01', '2016-10-10',
'2017-01-03', '2017-04-05', '2017-07-03', '2017-10-09',
'2018-01-02', '2018-04-02', '2018-07-02', '2018-10-08'],
dtype='datetime64[ns]', freq=None)
获取近5年按季度调仓日期
s_date,e_date = '2013-12-10','2018-12-10'
tradedays = get_tradeday_list(start=s_date,end=e_date,frequency="quarter",count=None)
tradedays
DatetimeIndex(['2014-01-02', '2014-04-01', '2014-07-01', '2014-10-08',
'2015-01-05', '2015-04-01', '2015-07-01', '2015-10-08',
'2016-01-04', '2016-04-01', '2016-07-01', '2016-10-10',
'2017-01-03', '2017-04-05', '2017-07-03', '2017-10-09',
'2018-01-02', '2018-04-02', '2018-07-02', '2018-10-08'],
dtype='datetime64[ns]', freq=None)
(2)优化目标说明
1)平均分仓
平均分仓就是对28个行业进行等权重资金配置
2)等波动率
等波动率是使得每个股票贡献的表征风险相等,如组合中第i个标的的权重为$w_i$,波动率为$w_i\sigma_i$
满足如下条件: $$ w_1\sigma_1 = w_2\sigma_2=...... =w_i\sigma_i$$
即权重应满足如下关系$$1/\sigma_1:1/\sigma_2:......:1/\sigma_i$$
3)最小方差
最小方差,也可以称为最小波动或最低风险
$w$为投资权重向量,$\Sigma$为各标的的收益率协方差矩阵
组合的波动率满足$\sigma = \sqrt{w^T\Sigma w }$,只要找到$w$使得$w^T\Sigma w $最小即可
4)风险平价
风险平价模型是通过衡量组合各标的对于组合的风险贡献度,来制定投资模型的各类资产权重。
风险平价的目标是均衡配置多个资产的风险,使得组合标的达到等风险贡献
5)最大夏普
夏普率用来表示每承受一单位风险,会产生多少的超额报酬,是对策略的收益与风险进行综合考虑。 $$SharpeRatio = {R_p-R_f\over\sigma_p}$$ $R_p 是策略年化收益, R_p = w_1r_1+w_2r_2+......+w_ir_i $
$R_f = 无风险利率(默认0.04)$
$\sigma_p 是策略收益波动率,\sigma_p = \sqrt{w^T\Sigma w }$
目标函数为 $$\smash{\displaystyle\max_{w}} {WR - R_f\over \sqrt{w^T\Sigma w}\sqrt{250}}$$
即寻找目标$w$,使得目标$(-1)*SharpeRatio$最小
接下来进行不同的优化目标,获取权重并保存记录
#计算调仓时权重配置并保存为字典
#记录加入权重后的组合收益时间序列
t0=dt.datetime.now()
weights_dict = {}
returns_df = pd.DataFrame()
num = 1
ret_daily = pct_daily+1
weights_name = ['mean_weights','mean_vol','min_var','risk_parity','max_sharpe']
for date_temp1,date_temp2 in zip(tradedays[:-1],tradedays[1:]):
t1=dt.datetime.now()
#获取指定日期一年前的交易日日期
def get_before_tradeday(date):
return get_price('000001.XSHG',end_date=date,count=252).index[0]
date_before = get_before_tradeday(date_temp1)
#最小方差
def fun1(x):
risk = np.dot(x.T,np.dot(cov_mat,x))
return risk
#最大夏普
def fun2(x):
r_b = 0.04
pct_mean = pct_temp.mean()
p_r = (1+np.dot(x,pct_mean))**250-1
p_sigma = np.sqrt(np.dot(x0.T,np.dot(cov_mat,x0))*250)
p_sharpe = (p_r-r_b)/p_sigma
return -p_sharpe
#风险平价
def fun3(x):
tmp = (omega * np.matrix(x).T).A1
risk = x * tmp/ np.sqrt(np.matrix(x) * omega * np.matrix(x).T).A1[0]
delta_risk = [sum((i - risk)**2) for i in risk]
return sum(delta_risk)
#计算协方差矩阵
pct_temp = pct_daily.loc[date_before:date_temp1,:]
cov_mat = pct_temp.cov()
omega = np.matrix(cov_mat.values)
#sicpy优化方法参数设置
x0 = np.ones(omega.shape[0]) / omega.shape[0]
bnds = tuple((0,None) for x in x0)
cons = ({'type':'eq', 'fun': lambda x: sum(x) - 1})
options={'disp':False, 'maxiter':1000, 'ftol':1e-20}
#平均分配权重
weights1 = np.array([1.0/pct_temp.shape[1]]*pct_temp.shape[1])
#等波动率
wts = 1/pct_temp.std()
weights2 = wts/wts.sum()
#模型求解组合方差最小时权重
weights3 = minimize(fun1,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
#风险平价
weights4 = minimize(fun3,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
#最大夏普
weights5 = minimize(fun2,x0,bounds=bnds,constraints=cons,method='SLSQP',options=options)['x']
weights_list = [weights1,weights2,weights3,weights4,weights5]
#统计收益
if num == 0:
returns1_df = pd.DataFrame()
for i in range(len(weights_list)):
weights_temp =[j if j > 0.0001 else 0.0 for j in weights_list[i]]
returns1_df[weights_name[i]] = (ret_daily.loc[date_temp1:date_temp2,:]*weights_temp).cumsum(axis=1).iloc[:,-1]
returns_df = pd.concat([returns_df,returns1_df],axis=0)
else:
#按权重的方式计算
for i in range(len(weights_list)):
weights_temp =[j if j > 0.0001 else 0.0 for j in weights_list[i]]
returns_df[weights_name[i]] = (ret_daily.loc[date_temp1:date_temp2,:]*weights_temp).cumsum(axis=1).iloc[:,-1]
num = 0
weights_dict[date_temp1] = weights_list
t2=dt.datetime.now()
print('计算到%s,已耗时%s秒'%(date_temp2,(t2-t1).seconds))
print('计算完毕,总耗时%s秒'%(t2-t0).seconds)
计算到2014-04-01 00:00:00,已耗时1秒 计算到2014-07-01 00:00:00,已耗时1秒 计算到2014-10-08 00:00:00,已耗时1秒 计算到2015-01-05 00:00:00,已耗时1秒 计算到2015-04-01 00:00:00,已耗时1秒 计算到2015-07-01 00:00:00,已耗时2秒 计算到2015-10-08 00:00:00,已耗时1秒 计算到2016-01-04 00:00:00,已耗时1秒 计算到2016-04-01 00:00:00,已耗时1秒 计算到2016-07-01 00:00:00,已耗时1秒 计算到2016-10-10 00:00:00,已耗时1秒 计算到2017-01-03 00:00:00,已耗时1秒 计算到2017-04-05 00:00:00,已耗时1秒 计算到2017-07-03 00:00:00,已耗时1秒 计算到2017-10-09 00:00:00,已耗时2秒 计算到2018-01-02 00:00:00,已耗时2秒 计算到2018-04-02 00:00:00,已耗时2秒 计算到2018-07-02 00:00:00,已耗时1秒 计算到2018-10-08 00:00:00,已耗时1秒 计算完毕,总耗时32秒
(1)不同组合优化方法下净值表现
returns_df.cumprod(axis=0).plot(figsize=(15,8))
<matplotlib.axes._subplots.AxesSubplot at 0x7f5e69599e48>
红色的线是等权重配置,可以看到最小方差、风险平价、等波动率优化后是有增益效果
紫色的线是最波动最小,即最小方差配置,净值表现最好
最大夏普和最小方差的是组合优化表现的两个极端
中间三种组合方法的区分度不是很明显,应该是行业间相关性过高的原因
mean_wts_df = pd.DataFrame()
meanvol_wts_df = pd.DataFrame()
minvar_wts_df = pd.DataFrame()
rp_wts_df = pd.DataFrame()
maxshp_wts_df = pd.DataFrame()
for date in weights_dict.keys():
#print(weights_dict[date][1])
mean_wts_df[date] = weights_dict[date][0]
meanvol_wts_df[date] = weights_dict[date][1]
minvar_wts_df[date] = weights_dict[date][2]
rp_wts_df[date] = weights_dict[date][3]
maxshp_wts_df[date] = weights_dict[date][4]
mean_wts_df = mean_wts_df.T
mean_wts_df.columns = list(hy_df['name'].values)
meanvol_wts_df = meanvol_wts_df.T
meanvol_wts_df.columns = list(hy_df['name'].values)
minvar_wts_df = minvar_wts_df.T
minvar_wts_df.columns = list(hy_df['name'].values)
rp_wts_df = rp_wts_df.T
rp_wts_df.columns = list(hy_df['name'].values)
maxshp_wts_df = maxshp_wts_df.T
maxshp_wts_df.columns = list(hy_df['name'].values)
下面对各种优化方法的权重配置进行展示
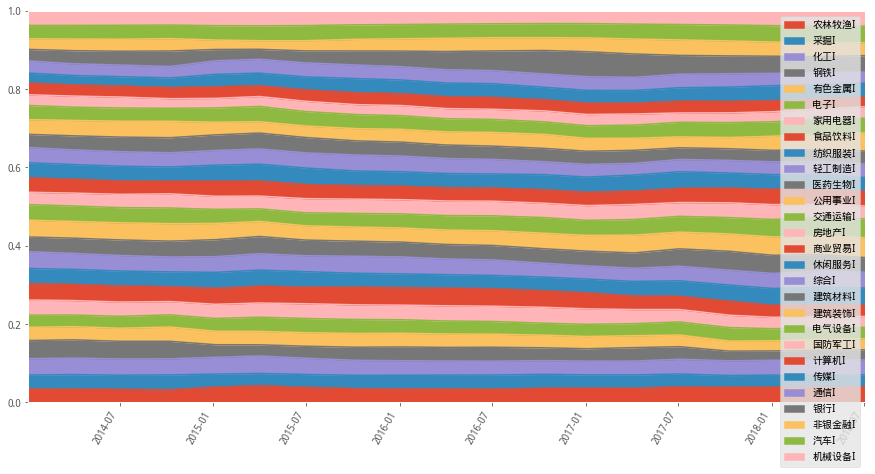
1)最小波动(最小方差)
#权重设置示意图
minvar_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
<matplotlib.axes._subplots.AxesSubplot at 0x7f5e69716da0>
组合长期对银行有较高的权重配置,尤其在2015年熊市之后不断进行权重增加,到2017年年初达到最大权重
下面我们贴一张同时期银行指数走势图
可以看到银行指数在2015年熊市之后逐步走强,尤其2016年到2017年的过程中涨幅明显超过上证指数
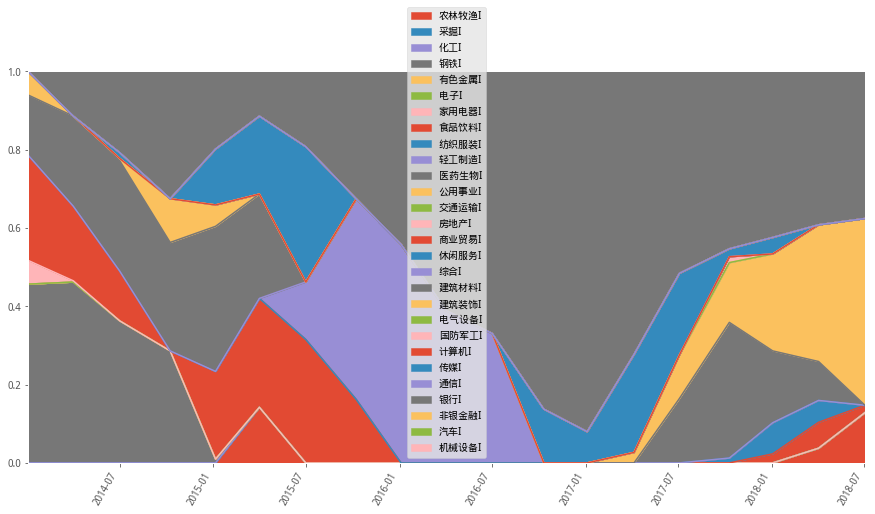
2)最大夏普
#权重设置示意图
maxshp_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
<matplotlib.axes._subplots.AxesSubplot at 0x7f5dab74c860>
从以上最大夏普和最小方差模型的配置权重中,可以看到有标的权重过于集中的情况
3)风险平价
#权重设置示意图
rp_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
<matplotlib.axes._subplots.AxesSubplot at 0x7f5e6b875b70>
4)等波动率
#权重设置示意图
meanvol_wts_df.plot(figsize=(15,8),rot=60,kind='area',ylim=(0,1))
<matplotlib.axes._subplots.AxesSubplot at 0x7f5e69483b38>
(2)收益风险指标汇总
#计算风险指标函数
def get_risk_index(pct_se):
return_se = pct_se.cumprod()-1
total_returns = return_se[-1]
total_an_returns = ((1+total_returns)**(250/len(return_se))-1)
vol = pct_se.std()*np.sqrt(250)
sharpe = (total_an_returns-0.04)/(np.std(pct_se)*250**0.5)
ret = return_se.dropna()
ret = ret+1
maxdown_list = []
for i in range(1,len(ret)):
low = min(ret[i:])
high = max(ret[0:i])
if high>low:
#print(high,low)
maxdown_list.append((high-low)/high)
#print((high-low)/high)
else:
maxdown_list.append(0)
max_drawdown = max(maxdown_list)
'''
print('策略收益:%s'%round(total_returns*100,2)+'%')
print('策略年化收益:%s'%round(total_an_returns*100,2)+'%')
print('夏普比率:%s'%round(sharpe,2))
print('最大回撤:%s'%round(max_drawdown*100,2)+'%')
print('年化波动率:%s'%round(vol,2))
'''
return total_returns,total_an_returns,sharpe,max_drawdown,vol
results=pd.DataFrame(index = ['策略收益','策略年化收益','夏普比率','最大回撤','年化波动率'])
for colu in returns_df.columns:
results[colu] = get_risk_index(returns_df[colu])
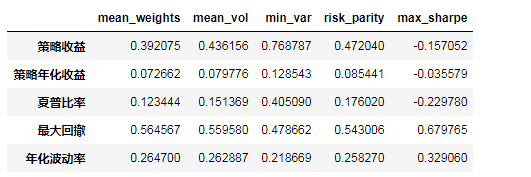
results
| mean_weights | mean_vol | min_var | risk_parity | max_sharpe | |
|---|---|---|---|---|---|
| 策略收益 | 0.392075 | 0.436156 | 0.768787 | 0.472040 | -0.157052 |
| 策略年化收益 | 0.072662 | 0.079776 | 0.128543 | 0.085441 | -0.035579 |
| 夏普比率 | 0.123444 | 0.151369 | 0.405090 | 0.176020 | -0.229780 |
| 最大回撤 | 0.564567 | 0.559580 | 0.478662 | 0.543006 | 0.679765 |
| 年化波动率 | 0.264700 | 0.262887 | 0.218669 | 0.258270 | 0.329060 |
通过对本研究中基于近5年申万行业指数时间序列的不同组合优化方法得出如下结论:
(1)进行组合优化处理后,均取得了优于平均分仓的效果
(2)最小方差组合效果显著,累计收益从39.2%提升至76.9%,年化收益从7.98%提升至12.85%,最大回撤从56.46%降低至40.51%,夏普比率从0.12提升至0.41
(3)几种优化方法整体提升效果一般,区分度不够明显,如年化波动0.2467略微降低至0.2187,最大回撤仅从56.46%优化到47.87%

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
