前言：在越来越多量化驱动的基金占据市场的情况下，Alpha的挖掘已经成为各个机构的重点关注对象。不久前JoinQuant上线了因子分析功能（在我的策略——单因子分析中能找到），使得用户能够测试自己的alpha，相比之前只能在回测模块挨个挨个测试每个指标而言，因子分析系统规避了回测的噪音、复杂的资产配置和交易系统产生的导致alpha失真的问题。下面是一个挖掘测试alpha并封装为策略的例子，供大家玩乐~

首先是代码部分，我们以最简单的交易量为例：

from jqfactor import Factor
class MONEY(Factor):
    name = 'ma'
    max_window = 1
    dependencies = ['money']
    def calc(self, data):
        ma = data['money'].mean()
        return zscore(ma) 

def zscore(series):
    std = series.std()
    mean = series.mean()
    return (series - mean)/std

注意该函数最终返回一定是一个pandas.Series对象，index为股票code，否则类将不能将变量传递导致报错。zscore函数将数据标准化。
如上，我们测试了股市中“热钱效应”的alpha, 发现该效应短时间内的预测效应较强。也即，单日成交额叫大的股票在未来短时间内上涨可能性更大。有兴趣的朋友们可以测试该alpha从05年到现在的效应，结果异常显著，但近期有颓势。

第一个指标，为收益。为了达到测试alpha是否有效的结果，我们往往会分层测试：将样本排序后划分为5类，每一类成为一个分位数，同时构建一个策略组合，分别测试其收益。热钱效应的分层测试结果如下：

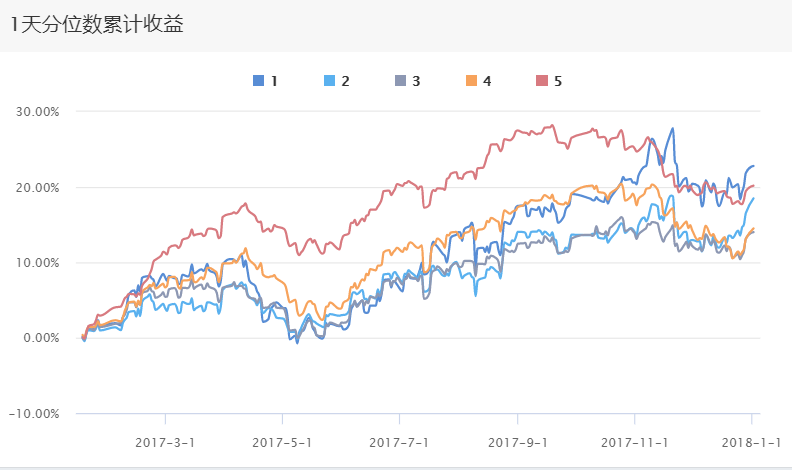
可见，单日成交额较大的个股赚钱效应较为显著，但是最近该因子有较为失效的趋势，这在一定程度上和市场风格有关。

在这一类指标下，我们还可以通过改变持仓的天数（也就是调仓的频率）分别测试收益：

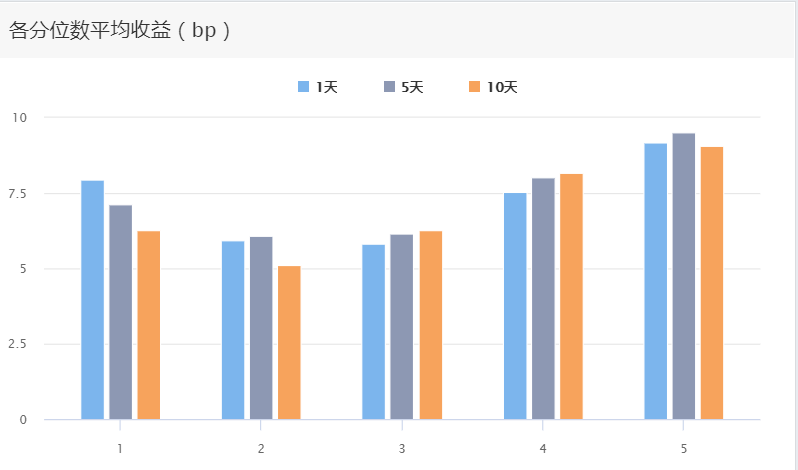
可见，热钱效应指标是一个极为短期的指标，在第二天赚钱效应明显。如果持有2~4天，收益明显下降。这也与技术面分析中高换手、高涨幅趋近于压力线增加的思想一致。

除此之外，还可以测试多空组合收益，即买多较好分位数的Porfolio并卖空较差分位数的Portfolio，其收益往往较只能多仓的A股市场表现更好。

另一个指标为Information Coefficient, 信息系数，衡量单个因子在全部股票的因子暴露值下与其下一期回报之间的关系，分为Norman IC (Pearson's Correlation)与Rank IC (Spearman's Correlation):

注：在JoinQuant平台中，IC为Rank IC

JP Morgan 2008: Multi-Factor Quant Model 有如下表述：

也即评估IC指标时往往会评估其月均线。

信息系数原本衡量统计学意义上的相关性或非相关性。在Quant的世界中，由于因子与下期收益率的相关性能够展示预测功能，IC也就用于衡量单个因子在全部股票的因子暴露值下的预期回报。

“热钱”因子的IC如下：

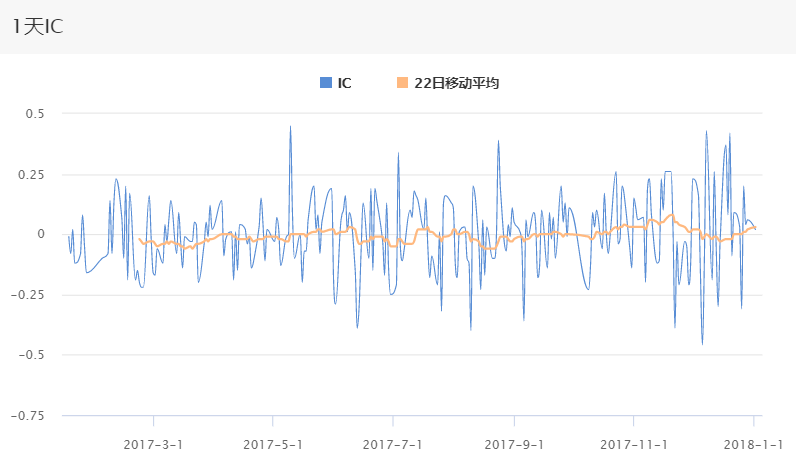
一般说来，IC的绝对值较大的话预测能力较好。本因子是最为初级的因子，本身具有的预测能力受大盘变动较大，相关系数值波动且较小，故而还需要一定的风格转换操作。

最后为换手率指标。换手率衡量调仓的频次。一般说来，换手率高，调仓越高，有利有弊。在达到更加主动的管理组合的同时也产生了高额的交易费用，同时对于价值类因子的效应产生没有给予充分的时间。

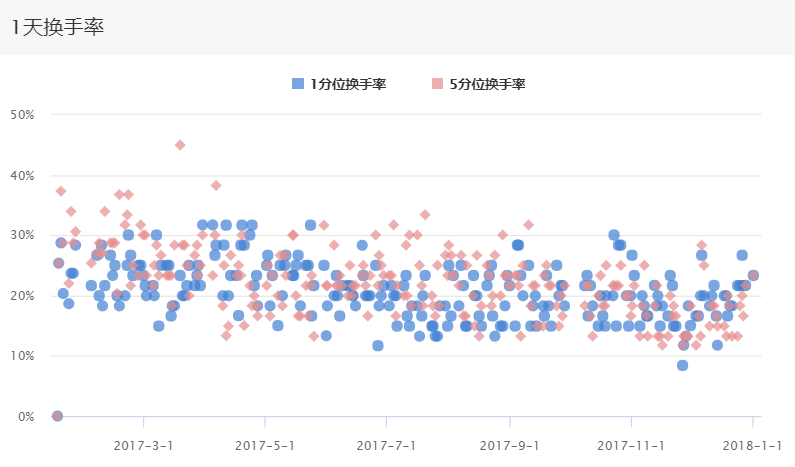
最后是该因子近一年的测试结果。在本测试中，设置等权重的交易量。事实上采取马科维茨配置等措施后收益和回撤表现将更为可观。该单个指标最近一年解释了0.065的alpha，但beta值较高（直觉而言高成交量也有可能是恐慌性抛盘、大量做空导致的，同时高成交量的股票也意味着行情更加震荡）。

期待JoinQuant的小伙伴们能够发掘出更多更加优质的alpha~