聚宽最近推出了场内期权数据功能。我翻出来之前自己写的一篇文章，谈一谈期权的定价原理，致敬一下新的场内期权数据。

原文：
《赌球“期权”是期权么？---从期权定价说起》20180716
上周末，朋友圈被一篇【“法国夺冠华帝免单”，一堂生动的“期权对冲”课】刷屏了，文章的阅读量突破30万。今天，从专业期权定价的角度，来分析一下赌球“期权”和金融期权的区别，帮助一些朋友进一步了解期权。
如果赌球是以赚钱为目的的，那么可以把赌球当做是一笔投资。既然是投资，就不得不提及无风险收益率，也就是保本保息理财的收益率，这是我们赌球的机会成本，我们先假设无风险收益率为0%。
假设法国队夺冠的概率是80%，赔率是1.25。如果把足彩看做是股票，那么今天的股价就是100元，未来80%概率股价升至125元，20%的概率股价降低至0元。那么你愿意以100元的价格买这只股票么？换言之，你会买该足彩么？

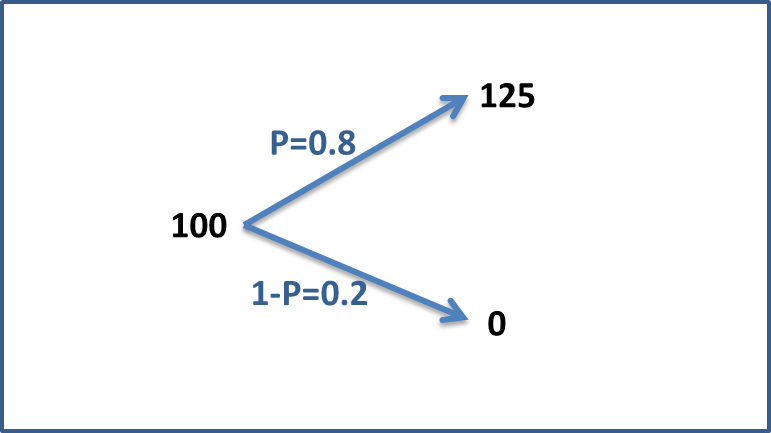
对于大多数厌恶风险的人来说，答案是“不会”。我们来算笔账，今天我花了100元买股票，而未来股价的预期依然为100元（125×80% ＋0×20%=100），即收益率为0%。若是我不买股票，我有100%的概率获取0%的预期收益。现在，我承担了风险（未来收益的不确定性），我的预期收益依然是0，这显然是不划算的。如果要让我买股票，必须要给我补偿额外收益，比如说我要25%的额外收益补偿我承担的风险。那么股票的期初价格将为80元（（125×80%＋ 0×20%）/(1＋25%）=80)。换算为足球赔率就是125/80=1.5625。
上述定价逻辑在理论上是完全严谨的。那么我们为什么不能用此方法对股票或期权进行估值呢。因为在真实市场，上述例子中80%的概率，25%的风险额外回报，并不是我们容易直接观察出来的。所以，运用上述方法对期权估值是走不通的。
我们回到一个股票的例子。假如股票期初价格为100元，1个月后60%的概率价格变为101元，,40%的概率价格为99元。若购买了该股票为标的的1个月期平值看涨期权，一个月后该期权60%的概率获得1元收益，40%的概率获得0元收益。那么期权的定价应该为多少。

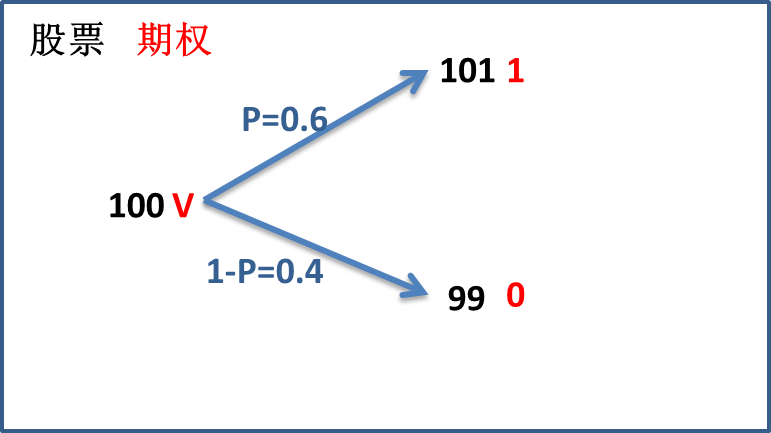
0.6元！！！！（60%×1＋40%×0=0.6）。答案显然是不对的，因为期权购买者会要求风险补偿收益。那么我们的估值方法希望用不到风险补偿收益和上涨概率这些参数。我们换一个思路。

首先，我不想用到上涨下跌概率这个参数。那么，我希望构建一个投资组合，无论上涨还是下跌，其价值是一样的。如何构建这个组合呢？假如我卖出一个看涨期权，价值为V。同时我买入Δ个股票。一个月后，我希望上涨和下跌组合的价值是一样的。可以算出Δ为0.5，我们需要买入0.5个股票。

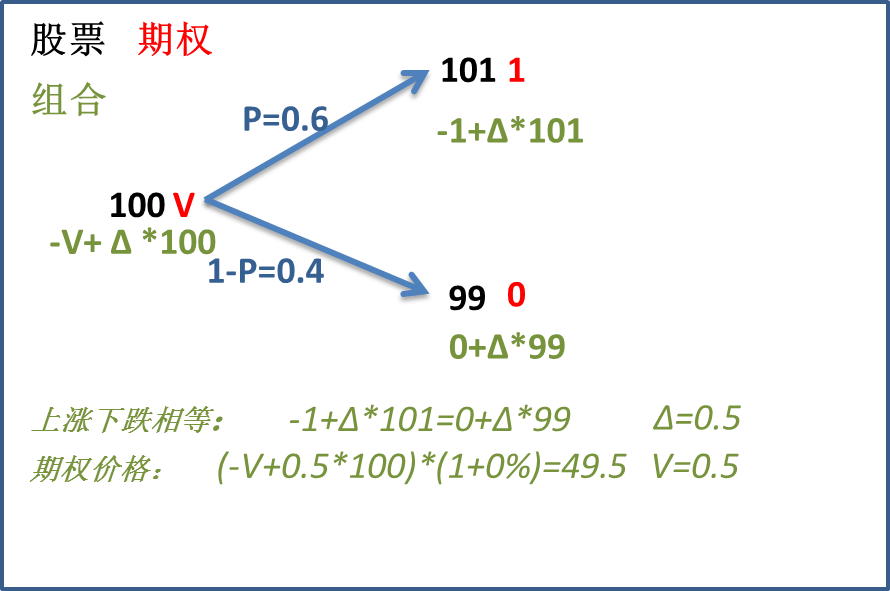
无论股价上涨还是下跌，我们在期末组合价值都为49.5。股价涨跌组合收益无差异，我们就不需要风险补偿，这时我们也跳过了风险补偿收益这个参数。那么我们的要求收益率就是无风险收益率，即0%。之后可以得到期权的价格为0.5。
通过构建一个投资组合，利用对冲的思想，绕过了股票上涨下跌概率，风险补偿收益参数难以估计的困难，最终达到期权定价的目的。这就是大名鼎鼎的Black-Scholes公式的思想。
在真实世界中，风险越大，要求的风险补偿收益就越高。上述例子符合这个规律么？当然！上述例子中，股票要求0.2%的风险补偿收益。期权要求了20%的风险补偿收益。
(101×0.6＋99×0.4)/100-1=0.2% (1×0.6＋0×0.4)/0.5-1=20%
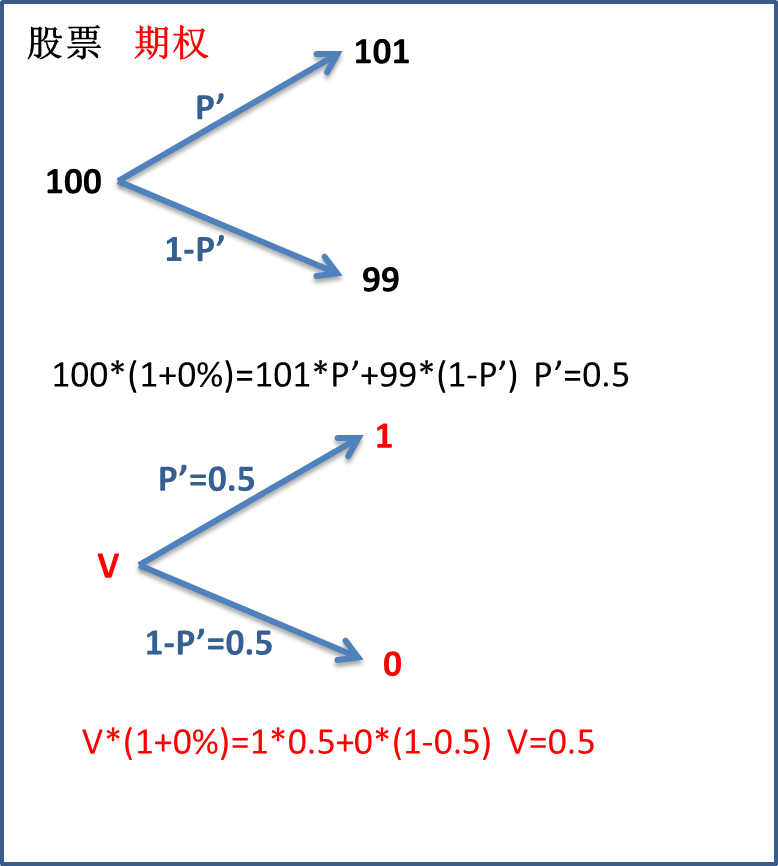
真实世界太复杂，如果我们能换个简单的世界多好，比如说不要求风险补偿收益。假如真的来到了一个不要求风险补偿的世界，我们的股价不得不发生变化。如果要求股价不变，那么股票上涨的概率必须要发生变化才可以保持平衡。我们假定股票上涨的概率为P’,通过计算，P’变为了0.5。在这个世界里，期权价格也可以很容易计算得到为0.5。这就是风险中性定价。风险中性的意思就是投资者承担风险但不需要补偿收益。

回到我们最早的讨论，赌球“期权”是期权么？从字面上来讲，期权是未来的权利。说赌球“期权”是期权没有错。但是在其背后的理论逻辑与期权是不一样的。华帝可以用赌球来对冲它的营销活动，但是博彩公司却无法对冲它的赌球合约。
在场外期权交易中，机构客户购买方对价格的态度取决于股票上涨的概率。而券商作为卖方，通过对冲风险，价格取决于对冲成本。双方交易的目的，关注焦点不同，所以双方才更容易达成交易。所以，场外期权交易并不是一场“零和博弈”，双方都可以从其中获利。而对于赌球“期权”而言，胜者赚的钱就是输者陪的钱，是一场“零和博弈”。
前几天遇到一个同事对我说，你们做衍生品的对于算概率什么的很在行，赌球会有优势吧。现在可以回答，当然不是，我们不在乎概率，只在乎对冲成本。