资产定价模型CAPM中假设投资标的收益率是正态分布，即大部分关注其均值-方差。但市场中的标的收益率不一定符合，也会出现尖峰厚尾、不对称性等现象。非对称的一个重要研究即是偏度（偏态）。表征概率分布密度曲线相对于平均值不对称程度的特征数。直观看来就是密度函数曲线尾部的相对长度。

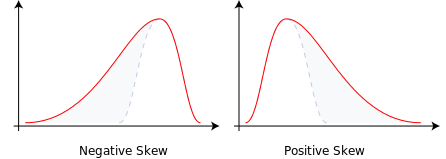
上图即是非对称的，一即是左偏，众数>中位数>平均数，数据位于均值左边的比位于右边的少，直观表现为左边的尾部相对于与右边的尾部要长。 二即是右偏，算术平均数>中位数>众数，数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于与左边。
偏度产生的原因在学界研究较少，一种说法是通过杠杆效应和波动反馈效应解释偏度的产生。
从传统的CAPM到Fama和French的三因子模型、各种市场异象、流动性溢价现象、动量效应等，关于影响收益的特征因子的研究一直以来都是金融领域的重点内容。资产收益的波动是特征因子之一，因此关于波动与收益之间的关系的研究也不少。较早进行研究的有Black(1976)、Christie(1982)，结果发现股票的收益与波动之间呈负相关。Engle和Ng(1993)研究则发现资产收益波动呈现不对称性，即正的收益一般伴随着条件方差向下的减少，而负的收益则伴随着条件方差向上的增大。这一现象在市场大跌时比较明显，因为市场波动会因股票价格大幅下跌而加剧。波动不对称性说明利空消息引起的波动大于利好消息引起的波动。
对波动不对称性的解释有“杠杆效应”和“波动反馈效应”。杠杆效应是指公司价值下降引起的股票价格下跌会提高公司的财务杠杆，公司股票的投资风险增大从而增加股票价格的波动性。而波动反馈效应则认为，如果在定价过程中考虑波动因素，那么对股票价格波动性预期的增加会提高投资者相应的收益补偿要求，这会导致股票价格的下降。而这两种效应只能解释收益分布的左偏现象，即“波动不对称性”只反应了收益分布的左偏现象，对于市场上广泛存在的收益分布的右偏现象则无法解释。
个股偏度能够解释股票收益的横截面变动，与股票收益之间呈显著的负向关系，投资者往往偏好收益分布右偏的证券。有一定概率获得较大的收益，即以小博大。

偏度的定义：3阶中心距与标注差的比值

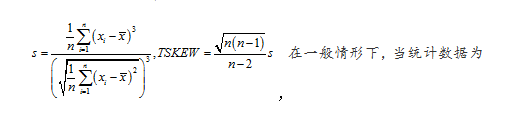
在一般情形下，当统计数据为右偏分布时，S_k > 0，且S_k值越大，右偏程度越高；当统计数据为左偏分布时，S_k < 0，且S_k值越小，左偏程度越高。当统计数据为对称分布时，显然有S_k = 0。

偏度在A股市场中的分布：

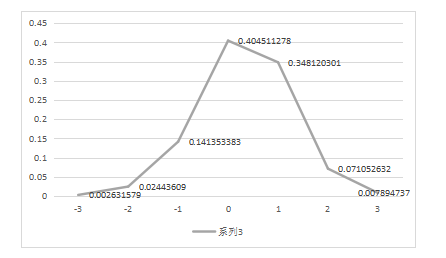
A股57.29%左偏，出现极端偏右值比偏左值要高5.18%。

在行业中分布：

源代码：

import numpy as np
import pandas as pd#if __name__=='__main__':dfall = get_all_securities(types=[], date='2018-12-04')
stocks = list(dfall.index)
skewcount2 = []for stock in stocks:if stock[0] != '6':
        df = get_price(stock,start_date=dfall['start_date'][stock],end_date='2018-12-04',frequency = 'daily',fields = ['close'])
        df = df.where(df.notnull(), df['close'][1])
        price = list(df['close'])
        report2 = []for i in range(len(price)-1):
            report2.append(price[i 1]-price[i])
        dfreport2 = pd.DataFrame(report2)
        skewcount2.append(dfreport2.skew())

left2 = sum([int(xi>0) for xi in skewcount2])
right2 = sum([int(xi<0) for xi in skewcount2])
rate2 = left2/(left2 right2)