全面了解多因子系列入门（一）¶

> 因子系列（一）
> 作者：孤傲同学

多因子入门¶

相信大家在提起量化模型的时候，听到最多的一个词就是“多因子”了，那么多因子模型究竟是一个什么样的模型呢，其中因子又是什么呢，该系列将一一从入门开始介绍多因子模型。

因子，顾名思义就是一个因素，各种各样的因子对于股票收益的贡献，就好比一些优秀特质对一个人的成功做出的贡献，例如我们可以简略的把一个人的成功归结于：勤奋，勇敢，创新，诚信等等。我们也可以把一只股票的收益归结于：该公司的市值，经营状况，财务状况等等。我们想要做的就是找到一些能够解释股票收益的因子，并且找出他们是如何影响股票收益的，以此找出规律，对未来的股票收益做出判断和预测例如：著名的Fama French 三因子模型即： $R_i-R_f=α_i+b_i (R_m-R_f )+s_i SMB+h_i HML+ε_i$
其中，市场因子：$(R_m-R_f )$ 市值因子：SMB ——小股票收益率-大股票收益率估值因子：HML——低估值股票收益率-高估值股票收益率为什么会选择这几个因子作为模型中的解释变量呢？是否还有其他的因子可以用来择股呢，且听我一一道来。

因子回测¶

那么我们找到的因子是否都是有效的呢，它们又以什么样的方式影响股票的收益率呢？为得到这些问题的答案，我们就需要对因子进行回测，来找出因子与股票收益率之间的关系。通常的因子回测方法有：因子回测方法.png

（检验因子A是否有择股能力）

排序法基本思路：¶

1.利用t-1时刻的数据计算出因子A 2.将股票按照A的大小进行排序 3.将股票分为高A组合和低A组合 4.持有不同的组合至t时刻，计算收益率 5.构造t统计量检验是否显著有差异

单变量排序¶

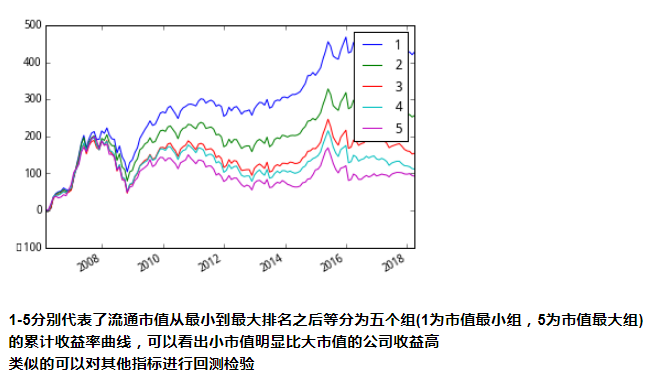
以下为以总市值和市净率（pb_ratio）作为因子进行的回测： 以总市值作为指标分组： QQ截图20180604120156.png 可以看出小市值组的收益率明显高于大市值组。

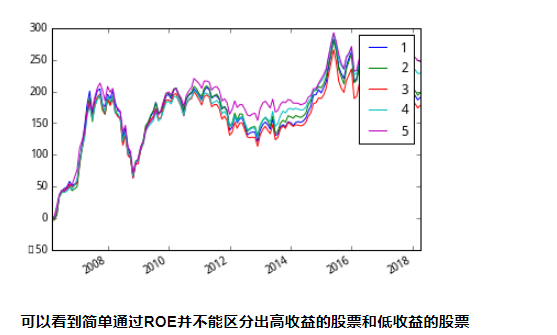
以ROE作为指标分组： QQ截图20180604120211.png 可以看出单独使用该指标难以区分股票优劣。

双变量排序¶

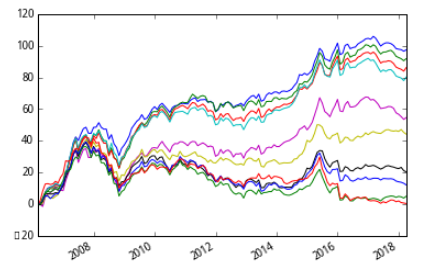
双变量序贯排序： 序贯排序.png 可以看出组间是有明显区别的

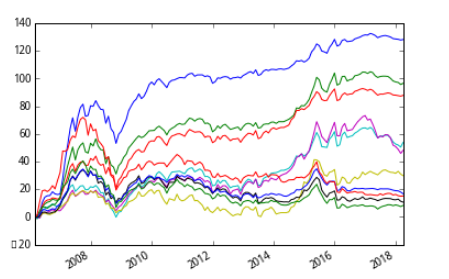
双变量独立排序： 独立排序.png 可以看出“低市净率+小市值”的组合收益率显著高于其他的组合。

双变量独立排序t检验： QQ截图20180604130630.png

当样本值很大时，t统计量依分布收敛到正态分布上，因此可以用正态分布的分位数来进行判断。通常样本数超过31个时可以按正态分布来计算。

由统计检验结果可见： 统计量：1.88672349 p值：0.02959876<0.05 由此可知在95%水平下两个组合的收益率有显著差异

未完待续。

下面是代码部分

import pandas as pd
import numpy as np
import datetime
import time
import matplotlib.pyplot as plt
from math import log,sqrt

全A股、去除停牌、ST
每月调仓
每月计算一次指标，获得股票池，同时计算出该月收益率
相当于每个截面比较一次，再把截面拉成时间序列

index = '000002.XSHG'#A股
benchmark = '000300.XSHG'#沪深300
#benchmark = '000016.XSHG'#上证50
#benchmark = '000010.XSHG' #上证180
#startDate = datetime.datetime(2006,1,1,9,30)
startDate = datetime.datetime(2006,1,1,9,30)
endDate = datetime.datetime(2018,3,1,9,30)
pointDate = datetime.datetime(2017,12,1,9,30)
stocklist = get_index_stocks(index)

#过滤停牌 and ST股票
def filterOfPauseAndST(stockList,startDate,endDate):
    import numpy as np
    unsuspendStock = []
    crew = get_price(stocklist, start_date=startDate, end_date=endDate, fields=['paused'])
    crew = crew.paused.T
    crew.rename(columns={crew.columns[0]:'paused'}, inplace=True)
    crew.dropna()
    pack = get_extras('is_st', stocklist, start_date=startDate, end_date=endDate, df=True)
    pack = pack.T
    pack.rename(columns={pack.columns[0]:'is_st'}, inplace=True)
    unsuspended = crew[crew['paused']==0].index
    unst = pack[pack['is_st']==False].index
    for stock in stockList:
        if (stock in unsuspended) and (stock in unst) :
                unsuspendStock.append(stock)
    return unsuspendStock

def calDRet(stocks,startDate,pointDate):
    #计算组合收益率，startDate为开始日期，pointDate为指定日期
    price = get_price(stocks,start_date=startDate,end_date=pointDate,fields='close')   
    ret = np.sum(np.log(price.close.tail(1).values/price.close.head(1).values))
    
    return ret
    #返回为一个n只股票的收益率之和

单变量排序
评估一个因子平均意义上是否对股票有区分能力
排序法：t-1时刻，在横截面按照指标排序
指标高的一组，指标低的一组，看t时刻（或t+j时刻）两组收益率是否存在单调关系

股票1 股票2 股票3 股票4

时间1 指标指标指标指标时间2 指标指标指标指标

####################################示例1##########################################

timestamp = pd.date_range(startDate,endDate,freq='M')
#按月建立时间戳index
u = filterOfPauseAndST(stocklist,startDate,endDate)#获得过滤后股票列表u

#流通市值
q=query(valuation.code,
        valuation.circulating_market_cap).filter(valuation.code.in_(u))

ret_1={}
ret_2={}
ret_3={}
ret_4={}
ret_5={}
for date in timestamp:
    df = get_fundamentals(q,date)
    df = df.set_index('code')
    sorteddf = df.sort(columns=['circulating_market_cap'])
    group1 = sorteddf.head(int(len(u)*0.2))
    group2 = sorteddf.iloc[131:263,:]
    group3 = sorteddf.iloc[263:394,:]
    group4 = sorteddf.iloc[394:525,:]
    group5 = sorteddf.iloc[525:,:]
    retdate = date+datetime.timedelta(days=30)
    ret_1[retdate] = calDRet(list(group1.index.values),date,retdate)
    ret_2[retdate] = calDRet(list(group2.index.values),date,retdate)
    ret_3[retdate] = calDRet(list(group3.index.values),date,retdate)
    ret_4[retdate] = calDRet(list(group4.index.values),date,retdate)
    ret_5[retdate] = calDRet(list(group5.index.values),date,retdate)

seri1 =pd.Series(ret_1)
seri2 =pd.Series(ret_2)
seri3 =pd.Series(ret_3)
seri4 =pd.Series(ret_4)
seri5 =pd.Series(ret_5)

seri1.cumsum().plot(label='1'),seri2.cumsum().plot(label='2'),seri3.cumsum().plot(label='3'),seri4.cumsum().plot(label='4'),seri5.cumsum().plot(label='5')
plt.legend()
#比较从2006年-2018年小市值公司股票收益和大市值公司股票收益的差别

<matplotlib.legend.Legend at 0x7f7b1e0dc890>

1-5分别代表了流通市值从最小到最大排名之后等分为五个组(1为市值最小组，5为市值最大组)
的累计收益率曲线，可以看出小市值明显比大市值的公司收益高
类似的可以对其他指标进行回测检验

#####################################示例2####################################
q1=query(valuation.code,
        indicator.roe).filter(valuation.code.in_(u))
retpb_1={}
retpb_2={}
retpb_3={}
retpb_4={}
retpb_5={}
for date in timestamp:
    df = get_fundamentals(q1,date)
    df = df.set_index('code')
    sorteddf = df.sort(columns=['roe'])
    gp1 = sorteddf.head(int(len(u)*0.2))
    gp2 = sorteddf.iloc[131:263,:]
    gp3 = sorteddf.iloc[263:394,:]
    gp4 = sorteddf.iloc[394:525,:]
    gp5 = sorteddf.iloc[525:,:]
    retdate = date+datetime.timedelta(days=30)
    retpb_1[retdate] = calDRet(list(gp1.index.values),date,retdate)
    retpb_2[retdate] = calDRet(list(gp2.index.values),date,retdate)
    retpb_3[retdate] = calDRet(list(gp3.index.values),date,retdate)
    retpb_4[retdate] = calDRet(list(gp4.index.values),date,retdate)
    retpb_5[retdate] = calDRet(list(gp5.index.values),date,retdate)
    
seri1 =pd.Series(retpb_1)
seri2 =pd.Series(retpb_2)
seri3 =pd.Series(retpb_3)
seri4 =pd.Series(retpb_4)
seri5 =pd.Series(retpb_5)

seri1.cumsum().plot(label='1'),seri2.cumsum().plot(label='2'),seri3.cumsum().plot(label='3'),seri4.cumsum().plot(label='4'),seri5.cumsum().plot(label='5')
plt.legend()

<matplotlib.legend.Legend at 0x7f7b1c912290>

可以看到简单通过ROE并不能区分出高收益的股票和低收益的股票

###############################序贯排序#####################################
q1=query(valuation.code,
        valuation.market_cap,
        valuation.pb_ratio).filter(valuation.code.in_(u))
retsubgp1_1={}
retsubgp1_2={}
retsubgp1_3={}
retsubgp1_4={}
retsubgp1_5={}
retsubgp5_1={}
retsubgp5_2={}
retsubgp5_3={}
retsubgp5_4={}
retsubgp5_5={}
for date in timestamp:
    df = get_fundamentals(q1,date)
    df = df.set_index('code')
    sorteddf = df.sort(columns=['market_cap'])
    gp1 = sorteddf.head(int(len(u)*0.2))
    gp2 = sorteddf.iloc[131:263,:]
    gp3 = sorteddf.iloc[263:394,:]
    gp4 = sorteddf.iloc[394:525,:]
    gp5 = sorteddf.iloc[525:,:]
    subgp11 = gp1.sort(columns=['pb_ratio']).head(int(131*0.2))
    subgp12 = gp1.sort(columns=['pb_ratio']).iloc[26:52,:]
    subgp13 = gp1.sort(columns=['pb_ratio']).iloc[52:78,:]
    subgp14 = gp1.sort(columns=['pb_ratio']).iloc[78:104,:]
    subgp15 = gp1.sort(columns=['pb_ratio']).iloc[104:130,:]
    subgp51 = gp5.sort(columns=['pb_ratio']).head(int(131*0.2))
    subgp52 = gp5.sort(columns=['pb_ratio']).iloc[26:52,:]
    subgp53 = gp5.sort(columns=['pb_ratio']).iloc[52:78,:]
    subgp54 = gp5.sort(columns=['pb_ratio']).iloc[78:104,:]
    subgp55 = gp5.sort(columns=['pb_ratio']).iloc[104:131,:]
    retdate = date+datetime.timedelta(days=30)
    retsubgp1_1[retdate] = calDRet(list(subgp11.index.values),date,retdate)
    retsubgp1_2[retdate] = calDRet(list(subgp12.index.values),date,retdate)
    retsubgp1_3[retdate] = calDRet(list(subgp13.index.values),date,retdate)
    retsubgp1_4[retdate] = calDRet(list(subgp14.index.values),date,retdate)
    retsubgp1_5[retdate] = calDRet(list(subgp15.index.values),date,retdate)
    retsubgp5_1[retdate] = calDRet(list(subgp51.index.values),date,retdate)
    retsubgp5_2[retdate] = calDRet(list(subgp52.index.values),date,retdate)
    retsubgp5_3[retdate] = calDRet(list(subgp53.index.values),date,retdate)
    retsubgp5_4[retdate] = calDRet(list(subgp54.index.values),date,retdate)
    retsubgp5_5[retdate] = calDRet(list(subgp55.index.values),date,retdate)


seri11 =pd.Series(retsubgp1_1)
seri12 =pd.Series(retsubgp1_2)
seri13 =pd.Series(retsubgp1_3)
seri14 =pd.Series(retsubgp1_4)
seri15 =pd.Series(retsubgp1_5)
seri51 =pd.Series(retsubgp5_1)
seri52 =pd.Series(retsubgp5_2)
seri53 =pd.Series(retsubgp5_3)
seri54 =pd.Series(retsubgp5_4)
seri55 =pd.Series(retsubgp5_5)

seri11.cumsum().plot(),seri12.cumsum().plot(),seri13.cumsum().plot(),seri14.cumsum().plot(),seri15.cumsum().plot()
seri51.cumsum().plot(),seri52.cumsum().plot(),seri53.cumsum().plot(),seri54.cumsum().plot(),seri55.cumsum().plot()

(<matplotlib.axes._subplots.AxesSubplot at 0x7f7b02910ad0>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7b02910ad0>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7b02910ad0>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7b02910ad0>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7b02910ad0>)

可以看出，经过两个指标序贯排序后，有显著的区分能力

##################################独立排序######################################
q1=query(valuation.code,
        valuation.market_cap,
        valuation.pb_ratio).filter(valuation.code.in_(u))
retsubgp1_1={}
retsubgp1_2={}
retsubgp1_3={}
retsubgp1_4={}
retsubgp1_5={}
retsubgp5_1={}
retsubgp5_2={}
retsubgp5_3={}
retsubgp5_4={}
retsubgp5_5={}
for date in timestamp:
    df = get_fundamentals(q1,date)
    df = df.set_index('code')
    sorteddf = df.sort(columns=['market_cap'])
    gp1 = sorteddf.head(int(len(u)*0.2))
    gp2 = sorteddf.iloc[131:263,:]
    gp3 = sorteddf.iloc[263:394,:]
    gp4 = sorteddf.iloc[394:525,:]
    gp5 = sorteddf.iloc[525:,:]
    
    sorteddf = df.sort(columns=['pb_ratio'])
    gpa = sorteddf.head(int(len(u)*0.2))
    gpb = sorteddf.iloc[131:263,:]
    gpc = sorteddf.iloc[263:394,:]
    gpd = sorteddf.iloc[394:525,:]
    gpe = sorteddf.iloc[525:,:]
    
    subgp11=list(set(gp1.index.values).intersection(set(gpa.index.values)))
    subgp12=list(set(gp1.index.values).intersection(set(gpb.index.values)))
    subgp13=list(set(gp1.index.values).intersection(set(gpc.index.values)))
    subgp14=list(set(gp1.index.values).intersection(set(gpd.index.values)))
    subgp15=list(set(gp1.index.values).intersection(set(gpe.index.values)))
    
    subgp51=list(set(gp5.index.values).intersection(set(gpa.index.values)))
    subgp52=list(set(gp5.index.values).intersection(set(gpb.index.values)))
    subgp53=list(set(gp5.index.values).intersection(set(gpc.index.values)))
    subgp54=list(set(gp5.index.values).intersection(set(gpd.index.values)))
    subgp55=list(set(gp5.index.values).intersection(set(gpe.index.values)))
    
    retdate = date+datetime.timedelta(days=30)
    retsubgp1_1[retdate] = calDRet(subgp11,date,retdate)
    retsubgp1_2[retdate] = calDRet(subgp12,date,retdate)
    retsubgp1_3[retdate] = calDRet(subgp13,date,retdate)
    retsubgp1_4[retdate] = calDRet(subgp14,date,retdate)
    retsubgp1_5[retdate] = calDRet(subgp15,date,retdate)
    retsubgp5_1[retdate] = calDRet(subgp51,date,retdate)
    retsubgp5_2[retdate] = calDRet(subgp52,date,retdate)
    retsubgp5_3[retdate] = calDRet(subgp53,date,retdate)
    retsubgp5_4[retdate] = calDRet(subgp54,date,retdate)
    retsubgp5_5[retdate] = calDRet(subgp55,date,retdate)


seri11 =pd.Series(retsubgp1_1)
seri12 =pd.Series(retsubgp1_2)
seri13 =pd.Series(retsubgp1_3)
seri14 =pd.Series(retsubgp1_4)
seri15 =pd.Series(retsubgp1_5)
seri51 =pd.Series(retsubgp5_1)
seri52 =pd.Series(retsubgp5_2)
seri53 =pd.Series(retsubgp5_3)
seri54 =pd.Series(retsubgp5_4)
seri55 =pd.Series(retsubgp5_5)

seri11.cumsum().plot(),seri12.cumsum().plot(),seri13.cumsum().plot(),seri14.cumsum().plot(),seri15.cumsum().plot()
seri51.cumsum().plot(),seri52.cumsum().plot(),seri53.cumsum().plot(),seri54.cumsum().plot(),seri55.cumsum().plot()

(<matplotlib.axes._subplots.AxesSubplot at 0x7f7af7b76f10>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7af7b76f10>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7af7b76f10>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7af7b76f10>,
 <matplotlib.axes._subplots.AxesSubplot at 0x7f7af7b76f10>)

可以看出，经过两个指标独立排序后，有显著的区分能力

###############t检验###############
from scipy.stats import norm
RH_bar1 = seri11.mean()
RL_bar5 = seri55.mean()
StdH1 = np.std(seri11)
StdL5 = np.std(seri55)

Std15 = np.sqrt((StdH1**2+StdL5**2)/len(seri55))
t_stat15 = (RH_bar1-RL_bar5)/Std15
print t_stat15
p15 = norm.sf(t_stat15)
print p15

1.88672349
0.0295987632576

由统计检验结果可见：
统计量：1.88672349
p值：0.02959876<0.05
由此可知在95%水平下两个组合的收益率有显著差异

量化交易吧 / 量化平台 帖子：3365825 新帖：0

全面了解多因子系列入门（一）

EA发表于：5 月 10 日 06：04回复(1)