粒子碰撞运动轨迹模型-价格变动的粒子级本源
我们都知道,价格变动是由买卖引起的,买卖的东西,无非就是成交量了,将成交量想象成粒子,假设某时间点 T 其待撞击粒子为V ,待撞击粒子为V 由T 时间内聚集形成,撞击粒子为V(V为T时间点内有效撞击量,也就是推动股价涨跌的有效成交量),T 时间内形成的价格差为|H|(若,T 时间点收盘价为C[-T ],|H|=|C[-T ]-C|),某时间点价格为C,上一时间点价格为C[-1],则:
待撞击粒子受到撞击粒子后及未受到下一次撞击前,其应产生运动轨迹高度h(应产生的价格变动),h=(|H|/V )V
实际应产生的价格变动 Y=(h C[-1])-C,
即:Y=((|C[-T ]-C|/V )V C[-1])-C
所以成交量与价格的简单数理关系-粒子碰撞运动轨迹模型公式为:
Y=((|C[-T ]-C|/V )*V C[-1])-C
其中T 为每一品种的属性系数,对T 的确认,需要大量的计算(我们一般办公计算机是无法完成的,计算数据量极大需要时间,当然这个T 的存在已经经过我的论证检验),Y为未知变量,V与V 为处于不断撤换(变化)中的隐形变量。(什么是推动股价涨跌的有效成交量,这个大家自己算了,如果来到金融市场连这个东西都没算过,可以洗洗去睡了)
以下是该公式的同花顺实现图:
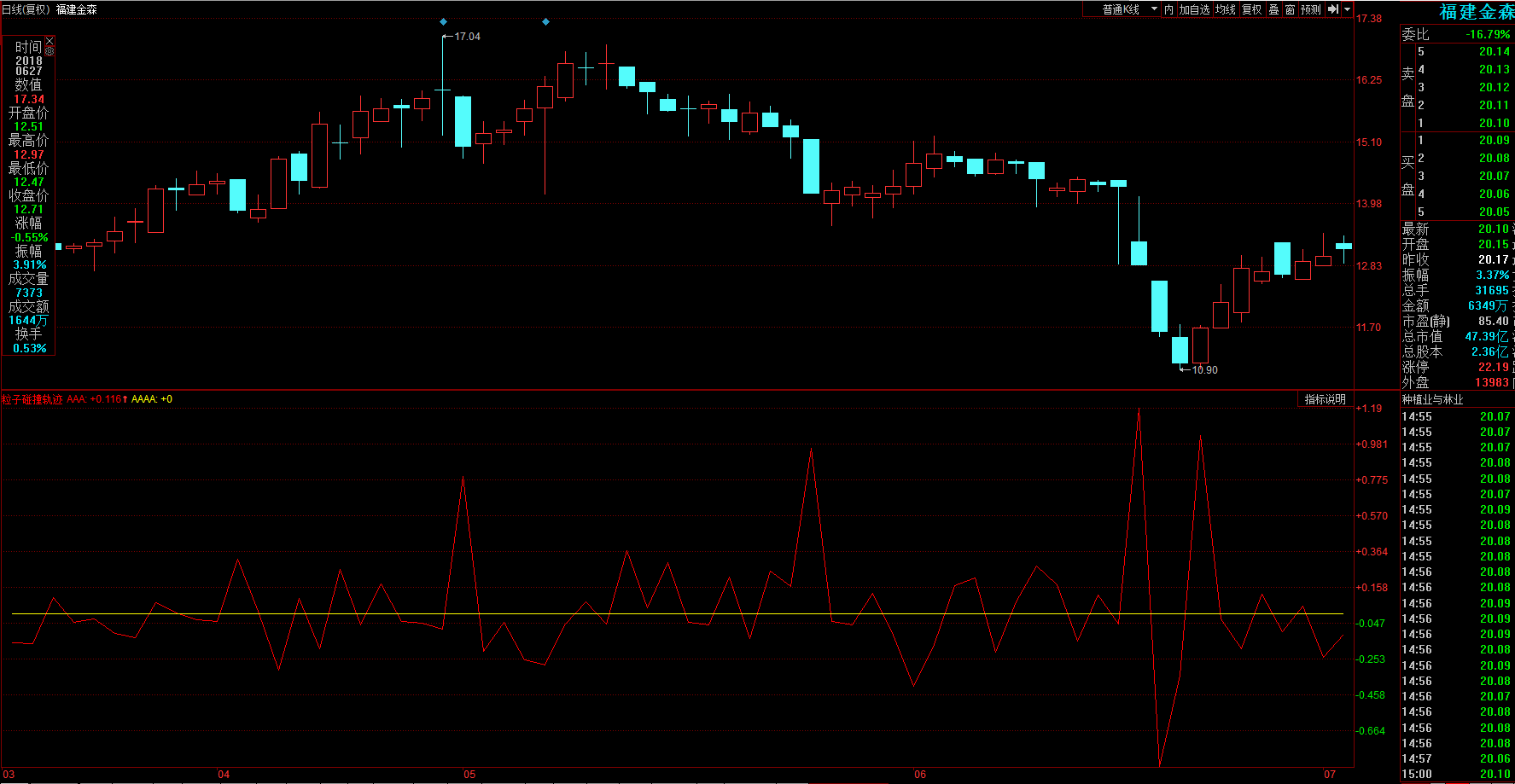
题外话(扯淡的笑话供娱乐):当我们计算得到Y时,无疑,Y是我们交易的绝佳超短线机会(这样的机会稍纵即逝),还可以进一步计算我们超短的介入量(西蒙斯的手法基本是超短加杠杆),进一步推算退出价格。因此我有理由相信文艺复兴极有可能使用了与粒子碰撞运动轨迹模型类似的模型。
注:本成交量与价格的简单数理关系-粒子碰撞运动轨迹模型版权为黄极所有,禁止他人以自创之名转载,转载引用请标注出自黄极!!!!