#模拟生成两个的权重
def weight(n):
w = np.random.random(n)
return w/sum(w)
#定义计算收益、风险、夏普率的函数
def portfolio_test(w):
r1,r2 = 0.08,0.12
sigma1,sigma2 = 0.12,0.25
rho1,rho2,rho3,rho4,rho5 = -1,-0.5,0,0.5,1
p_mean = r1*w[0] r2*w[1]
p_var1 = (w[0]**2)*(sigma1**2) (w[1]**2)*(sigma2**2) 2*w[0]*w[1]*rho1*sigma1*sigma2
p_var2 = (w[0]**2)*(sigma1**2) (w[1]**2)*(sigma2**2) 2*w[0]*w[1]*rho2*sigma1*sigma2
p_var3 = (w[0]**2)*(sigma1**2) (w[1]**2)*(sigma2**2) 2*w[0]*w[1]*rho3*sigma1*sigma2
p_var4 = (w[0]**2)*(sigma1**2) (w[1]**2)*(sigma2**2) 2*w[0]*w[1]*rho4*sigma1*sigma2
p_var5 = (w[0]**2)*(sigma1**2) (w[1]**2)*(sigma2**2) 2*w[0]*w[1]*rho5*sigma1*sigma2
p_sigma1 = np.sqrt(p_var1)
p_sigma2= np.sqrt(p_var2)
p_sigma3 = np.sqrt(p_var3)
p_sigma4 = np.sqrt(p_var4)
p_sigma5 = np.sqrt(p_var5)
return w[0],w[1],p_mean,p_sigma1,p_sigma2,p_sigma3,p_sigma4,p_sigma5
df_value =np.column_stack([portfolio_test(weight(2)) for i in range(10)]) #产生随机组合
df = pd.DataFrame(df_value.T,columns = ['A资产比例','B资产比例','r_期望收益','p_rho1','p_rho2','p_rho3','p_rho4','p_rho5'])
随机取了十组权重,计算组合收益和风险,其中A、B资产的权重之和为1,
组合收益为
组合风险为
计算之后结果如下图所示
给出的10组测试中,每组组合权重相同的情况下,预期收益是一样的,组合风险从1到5逐渐增加,即两资产的相关系数越高,风险越大,下图是十组收益在不同相关系数下的标准差值,可以清楚的看到-1最小而1最大
其实如果存在两个标的收益相关系数为-1,则组合收益理论上相互抵消了,所以在实际当中,能够寻找到低相关且都有正收益的标的就是极好的,分散化投资降低风险,其实就是在寻找相关度低的资产作为投资标的,在保证期望收益损失较小的情况下最大化的降低组合风险。
在这个例子中,我们取更多组的权重进行模拟,来观察下组合的期望收益和组合风险的变化情况
df_value1 =np.column_stack([portfolio_test(weight(2)) for i in range(200)]) #产生随机组合
df1= pd.DataFrame(df_value1.T,columns = ['A资产比例','B资产比例','p_mean','p_rho1','p_rho2','p_rho3','p_rho4','p_rho5'])
plt.scatter(df1['p_rho1'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho2'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho3'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho4'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho5'],df1['p_mean'],marker = 'o')
在不同的相关系数下,投资组合标准差随投资比例变动的情况呈现如上关系,横轴为组合标准差值,纵轴为组合期望收益值,除去最外面和最里边极端 -1的相关系数下的线性关系外,组合的预期收益和风险呈现的样子就是著名的Markowitz均值-方差模型里面的子弹图雏形了。
#选出几个标的数据,进行演示计算
#这里选取HS300里面近一年涨幅大于4%的5只股票
stock_list = get_index_stocks('000300.XSHG')
pool = []
for i in stock_list:
price_df = get_price(i,start_date='2017-9-1',end_date='2018-9-1',fields=['close'])
pct = price_df['close'].values[-1]/price_df['close'].values[0]
if pct>1.04:
pool.append(i)
if len(pool)==5:
break
pool
#数据准备
#计算股票池的涨跌幅、回报率
def get_return(pool):
prices = get_price(list(pool), end_date='2017-9-1', frequency='1d', fields=['close'],count=252).close
returns = (prices/prices.shift(1)).iloc[1:]
rets = returns.dropna(axis=1)
return rets
#随机权重设置
def weight(n):
w = np.random.random(n)
return w/sum(w)
#获取回报值
returns = get_return(pool)
#输入收益returns,权重
#返回年化收益、标准差、夏普率
def portfolio(returns,w):
#无风险收益年化设置为0.04
r_b = 0.04
returns = np.log(returns)
r_mean = returns.mean()*252
p_mean = np.sum(r_mean*w)
r_cov = returns.cov()*252
p_var = np.dot(w.T,np.dot(r_cov,w))
p_std = np.sqrt(p_var)
p_sharpe = (p_mean-r_b)/p_std
return p_mean,p_std,p_sharpe
step4 蒙特卡洛模拟
p_mean,p_std,p_sharpe = np.column_stack([portfolio(returns,weight(5)) for i in range(2000)]) #产生随机组合
plt.figure(figsize = (14,8))
plt.scatter(p_std, p_mean, c=p_sharpe, marker = 'o')
plt.grid(True) #显示网格
plt.xlabel('std')
plt.ylabel('mean')
plt.colorbar(label = 'Sharpe')
plt.title('Mean and Std of Returns')
将随机权重的组合收益风险进行图形化展示
step5 找出风险最小的组合权重、找出夏普率最大的组合权重
from scipy.optimize import minimize
#最小方差函数
def min_variance(w):
return portfolio(returns,w)[1]**2
#最大夏普函数(转化为求最小值)
def min_sharpe(w):
return -portfolio(returns,w)[2]
#约束条件,权重总和为1
cons = ({'type':'eq', 'fun':lambda x: np.sum(x)-1})
#夏普率最大
opt_sharpe = minimize(min_sharpe,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons)
#方差最小
opt_var = minimize(min_variance,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons)
step6 找出有效前沿
#有效前沿
#最小方差下的收益率
r_min = portfolio(returns,opt_var['x'])[0]
r_mean_list = np.linspace(r_min,r_min*1.7,20)
v_list = []
for r in r_mean_list:
cons1 = ({'type':'eq','fun':lambda w:portfolio(returns,w)[0]-r},{'type':'eq','fun':lambda w:np.sum(w)-1})
opt_var_1 = minimize(min_variance,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons1)
#最小方差下的收益率
v_min = portfolio(returns,opt_var_1['x'])[1]
print v_min
v_list.append(v_min)
有这么一个策略,每月换仓HS300前5只涨幅超过4%的股票进行买入持仓,具体操作如下
代码较长可以在研究里面参考,组合模拟结果如下
#计算总收益率
total_return1,total_return2 = df_returns.cumprod().values[-1]-1,df_a.cumprod().values[-1]-1
#计算年化收益
total_a_r1,total_a_r2 = (1 total_return1)**(250.0/len(df_returns))-1,(1 total_return2)**(250.0/len(df_a))-1
#计算夏普率
sharpe1,sharpe2 = (total_a_r1-0.04)/np.std(df_returns.cumprod()),(total_a_r2-0.04)/np.std(df_a.cumprod())
df_summary = pd.DataFrame([],index=['均值方差优化组合','平均分仓组合'])
df_summary['总收益'] = [total_return1,total_return2]
df_summary['年化收益'] = [total_a_r1,total_a_r2]
df_summary['sharpe'] = [sharpe1,sharpe2]
df_summary
可以看到优化后的组合获得了更好的表现
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
#模拟生成两个的权重
def weight(n):
w = np.random.random(n)
return w/sum(w)
#定义计算收益、风险、夏普率的函数
def portfolio_test(w):
r1,r2 = 0.08,0.12
sigma1,sigma2 = 0.12,0.25
rho1,rho2,rho3,rho4,rho5 = -1,-0.5,0,0.5,1
p_mean = r1*w[0]+r2*w[1]
p_var1 = (w[0]**2)*(sigma1**2)+(w[1]**2)*(sigma2**2)+2*w[0]*w[1]*rho1*sigma1*sigma2
p_var2 = (w[0]**2)*(sigma1**2)+(w[1]**2)*(sigma2**2)+2*w[0]*w[1]*rho2*sigma1*sigma2
p_var3 = (w[0]**2)*(sigma1**2)+(w[1]**2)*(sigma2**2)+2*w[0]*w[1]*rho3*sigma1*sigma2
p_var4 = (w[0]**2)*(sigma1**2)+(w[1]**2)*(sigma2**2)+2*w[0]*w[1]*rho4*sigma1*sigma2
p_var5 = (w[0]**2)*(sigma1**2)+(w[1]**2)*(sigma2**2)+2*w[0]*w[1]*rho5*sigma1*sigma2
p_sigma1 = np.sqrt(p_var1)
p_sigma2= np.sqrt(p_var2)
p_sigma3 = np.sqrt(p_var3)
p_sigma4 = np.sqrt(p_var4)
p_sigma5 = np.sqrt(p_var5)
return w[0],w[1],p_mean,p_sigma1,p_sigma2,p_sigma3,p_sigma4,p_sigma5
df_value =np.column_stack([portfolio_test(weight(2)) for i in range(10)]) #产生随机组合
df = pd.DataFrame(df_value.T,columns = ['A资产比例','B资产比例','r_期望收益','p_rho1','p_rho2','p_rho3','p_rho4','p_rho5'])
df
| A资产比例 | B资产比例 | p_mean | p_rho1 | p_rho2 | p_rho3 | p_rho4 | p_rho5 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.698865 | 0.301135 | 0.092045 | 0.008580 | 0.079920 | 0.112698 | 0.137893 | 0.159148 |
| 1 | 0.668762 | 0.331238 | 0.093250 | 0.002558 | 0.081561 | 0.115316 | 0.141221 | 0.163061 |
| 2 | 0.416181 | 0.583819 | 0.103353 | 0.096013 | 0.128482 | 0.154263 | 0.176313 | 0.195896 |
| 3 | 0.828637 | 0.171363 | 0.086855 | 0.056596 | 0.086389 | 0.108273 | 0.126423 | 0.142277 |
| 4 | 0.525211 | 0.474789 | 0.098992 | 0.055672 | 0.102861 | 0.134392 | 0.159819 | 0.181723 |
| 5 | 0.220925 | 0.779075 | 0.111163 | 0.168258 | 0.182960 | 0.196565 | 0.209287 | 0.221280 |
| 6 | 0.559924 | 0.440076 | 0.097603 | 0.042828 | 0.096055 | 0.128914 | 0.154955 | 0.177210 |
| 7 | 0.654125 | 0.345875 | 0.093835 | 0.007974 | 0.082770 | 0.116783 | 0.142918 | 0.164964 |
| 8 | 0.235294 | 0.764706 | 0.110588 | 0.162941 | 0.178739 | 0.193250 | 0.206745 | 0.219412 |
| 9 | 0.584404 | 0.415596 | 0.096624 | 0.033770 | 0.091797 | 0.125351 | 0.151655 | 0.174027 |
df[['p_rho1','p_rho2','p_rho3','p_rho4','p_rho5']].plot()
<matplotlib.axes._subplots.AxesSubplot at 0x7f7a452da610>
给出的10组测试中,每组组合的预期收益是一样的,组合风险从1到4逐渐增加,两资产的相关系数越高,风险越大。
df_value1 =np.column_stack([portfolio_test(weight(2)) for i in range(200)]) #产生随机组合
df1= pd.DataFrame(df_value1.T,columns = ['A资产比例','B资产比例','p_mean','p_rho1','p_rho2','p_rho3','p_rho4','p_rho5'])
plt.scatter(df1['p_rho1'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho2'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho3'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho4'],df1['p_mean'],marker = 'o')
plt.scatter(df1['p_rho5'],df1['p_mean'],marker = 'o')
<matplotlib.collections.PathCollection at 0x7f7a98957990>
以上是不同的相关系数下,投资组合标准差随投资比例变动的情况
接下来是马科维兹均值方差模型
从上面部分我们看到,几种资产的相关度越低,他们的组合收益?
#选出几个标的数据,进行演示计算
#这里选取HS300里面近一年涨幅大于4%的5只股票
stock_list = get_index_stocks('000300.XSHG')
pool = []
for i in stock_list:
price_df = get_price(i,start_date='2017-9-1',end_date='2018-9-1',fields=['close'])
pct = price_df['close'].values[-1]/price_df['close'].values[0]
if pct>1.04:
pool.append(i)
if len(pool)==5:
break
pool
[u'000002.XSHE', u'000333.XSHE', u'000338.XSHE', u'000425.XSHE', u'000786.XSHE']
#数据准备
#计算股票池的涨跌幅、回报率
def get_return(pool):
prices = get_price(list(pool), end_date='2017-9-1', frequency='1d', fields=['close'],count=252).close
returns = (prices/prices.shift(1)).iloc[1:]
rets = returns.dropna(axis=1)
return rets
#随机权重设置
def weight(n):
w = np.random.random(n)
return w/sum(w)
#获取回报值
returns = get_return(pool)
1.计算取的是对数收益率,研究中收益率都是用对数收益率,理论上对数收益率才是正态分布 2.求组合的方差、组合的标准差。 求方差时是收益率序列的协方差矩阵加权出来,并年化(*252)的。
np.log(returns).mean()*252
000002.XSHE 0.106476 000333.XSHE 0.042645 000338.XSHE 0.208467 000425.XSHE 0.081795 000786.XSHE 0.103304 dtype: float64
#输入收益returns,权重
#返回年化收益、标准差、夏普率
def portfolio(returns,w):
#无风险收益年化设置为0.04
r_b = 0.04
returns = np.log(returns)
r_mean = returns.mean()*252
p_mean = np.sum(r_mean*w)
r_cov = returns.cov()*252
p_var = np.dot(w.T,np.dot(r_cov,w))
p_std = np.sqrt(p_var)
p_sharpe = (p_mean-r_b)/p_std
return p_mean,p_std,p_sharpe
p_mean,p_std,p_sharpe = np.column_stack([portfolio(returns,weight(5)) for i in range(2000)]) #产生随机组合
plt.figure(figsize = (14,8))
plt.scatter(p_std, p_mean, c=p_sharpe, marker = 'o')
plt.grid(True) #显示网格
plt.xlabel('std')
plt.ylabel('mean')
plt.colorbar(label = 'Sharpe')
plt.title('Mean and Std of Returns')
<matplotlib.text.Text at 0x7f7a940f2850>
找到方差最小的点
optimize.minimize(target_fun,init_val,method,jac,hess) target_fun:函数的表达式计算; init_val:初始值; method:最小化的算法; jac:雅各比矩阵 hess:黑塞矩阵。
from scipy.optimize import minimize
#最小方差函数
def min_variance(w):
return portfolio(returns,w)[1]**2
#最大夏普函数(转化为求最小值)
def min_sharpe(w):
return -portfolio(returns,w)[2]
#约束条件,权重总和为1
cons = ({'type':'eq', 'fun':lambda x: np.sum(x)-1})
#夏普率最大
opt_sharpe = minimize(min_sharpe,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons)
#方差最小
opt_var = minimize(min_variance,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons)
print("Sharpe最大时的组合最优解是:")
print "组合仓位比例:",'%s' % (opt_sharpe['x'].round(3))
print('组合收益:%s' % (portfolio(returns,opt_sharpe['x'].round(3))[0]))
print('组合标准差(波动率):%s' % (portfolio(returns,opt_sharpe['x'].round(3))[1]) )
print('组合sharpe:%s' % (portfolio(returns,opt_sharpe['x'].round(3))[2]) )
Sharpe最大时的组合最优解是: 组合仓位比例: [ 0. 0.383 0.471 0. 0.147] 组合收益:0.489976378043 组合标准差(波动率):0.204062548869 组合sharpe:2.20509045161
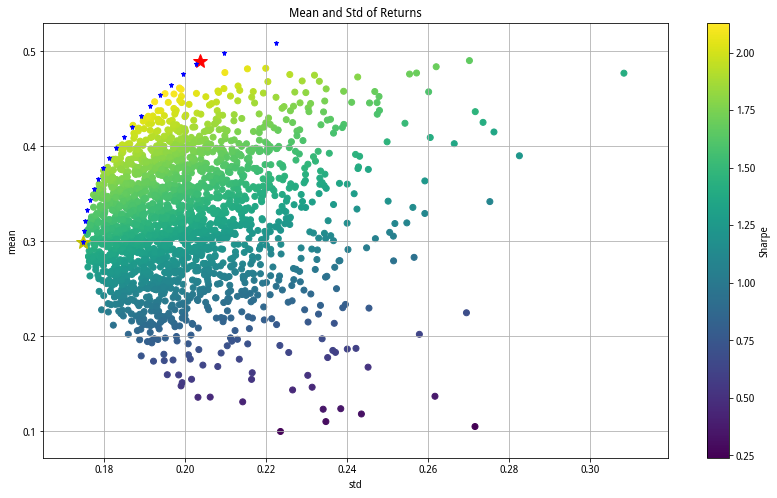
plt.figure(figsize = (14,8))
plt.scatter(p_std, p_mean, c=p_sharpe, marker = 'o')
#红星:标记最高sharpe组合
plt.plot(portfolio(returns,opt_sharpe['x'])[1],portfolio(returns,opt_sharpe['x'])[0], 'r*', markersize = 15.0)
#黄星:标记最小方差组合
plt.plot(portfolio(returns,opt_var['x'])[1], portfolio(returns,opt_var['x'])[0], 'y*', markersize = 15.0)
plt.grid(True) #显示网格
plt.xlabel('std')
plt.ylabel('mean')
plt.colorbar(label = 'Sharpe')
plt.title('Mean and Std of Returns')
<matplotlib.text.Text at 0x7f7a467ec210>
#有效前沿
#最小方差下的收益率
r_min = portfolio(returns,opt_var['x'])[0]
r_mean_list = np.linspace(r_min,r_min*1.7,20)
v_list = []
for r in r_mean_list:
cons1 = ({'type':'eq','fun':lambda w:portfolio(returns,w)[0]-r},{'type':'eq','fun':lambda w:np.sum(w)-1})
opt_var_1 = minimize(min_variance,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons1)
#最小方差下的收益率
v_min = portfolio(returns,opt_var_1['x'])[1]
print v_min
v_list.append(v_min)
0.175019898941 0.175114714577 0.175411195452 0.175913650611 0.176615582056 0.177519122871 0.178616014397 0.179908116449 0.181387427862 0.183051479008 0.184894460286 0.186910174387 0.18909558519 0.191441857239 0.193945694052 0.196649131372 0.199629477745 0.202879148981 0.209608338398 0.222411666394
plt.figure(figsize = (14,8))
plt.scatter(p_std, p_mean, c=p_sharpe, marker = 'o')
#红星:标记最高sharpe组合
plt.plot(portfolio(returns,opt_sharpe['x'])[1],portfolio(returns,opt_sharpe['x'])[0], 'r*', markersize = 15.0)
#黄星:标记最小方差组合
plt.plot(portfolio(returns,opt_var['x'])[1], portfolio(returns,opt_var['x'])[0], 'y*', markersize = 15.0)
#标记有效前沿
plt.plot(v_list,r_mean_list, 'b*', markersize = 5.0)
plt.grid(True) #显示网格
plt.xlabel('std')
plt.ylabel('mean')
plt.colorbar(label = 'Sharpe')
plt.title('Mean and Std of Returns')
<matplotlib.text.Text at 0x7f7a464d38d0>
#最小方差下的收益率
r_min = portfolio(returns,opt_var['x'])[0]
r_min
0.300883836813862
一个示例 1.取HS300前一年涨幅超过4%的5只股票 2.每月调仓,更换股票池 3.在同一个股票池下,A组合平均分仓,B组合取最大夏普权重 4.比较股票收益的波动情况和年化收益
#输入日期
#返回HS300中股票收益超过4%的前5只股票
def get_pool(date):
stock_list = get_index_stocks('000300.XSHG',date=date)
pool = []
for i in stock_list:
price_df = get_price(i,end_date=date,fields=['close'],count=252)
pct = price_df['close'].values[-1]/price_df['close'].values[0]
if pct>1.04:
pool.append(i)
if len(pool)==5:
break
return pool
#输入股票列表
#返回一个组合的权重配比
def opt_func(pool,date):
prices = get_price(list(pool), end_date=date, frequency='1d', fields=['close'],count=252).close
returns = (prices/prices.shift(1)).iloc[1:]
returns = returns.dropna(axis=1)
def portfolio(returns,w):
#无风险收益年化设置为0.04
r_b = 0.04
returns = np.log(returns)
r_mean = returns.mean()*252
p_mean = np.sum(r_mean*w)
r_cov = returns.cov()*252
p_var = np.dot(w.T,np.dot(r_cov,w))
p_std = np.sqrt(p_var)
p_sharpe = (p_mean-r_b)/p_std
return p_mean,p_std,p_sharpe
def weight(n):
w = np.random.random(n)
return w/sum(w)
#最大夏普函数(转化为求最小值)
def min_sharpe(w):
return -portfolio(returns,w)[2]
#约束条件,权重总和为1
cons = ({'type':'eq', 'fun':lambda x: np.sum(x)-1})
#夏普率最大
opt_sharpe = minimize(min_sharpe,weight(5),bounds=((0,1),(0,1),(0,1),(0,1),(0,1)),constraints = cons)
return opt_sharpe['x'].round(3)
date = '2018-1-1'
pool = get_pool(date)
res = opt_func(pool,date).round(3)
res
array([ 0.314, 0.204, 0.482, 0. , 0. ])
#工具函数
#获取日期列表
def get_tradeday_list(s='2017-1-1',e='2018-7-25',label='month',count=None):
if count != None:
df = get_price('000001.XSHG',end_date=e,count=count)
else:
df = get_price('000001.XSHG',start_date=s,end_date=e)
if label==None:
return df.index
else:
df['year-month'] = [str(i)[0:7] for i in df.index]
if label == 'month':
return df.drop_duplicates('year-month').index
elif label == 'quarter':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='04') | (df['month']=='07') | (df['month']=='10') ]
return df.drop_duplicates('year-month').index
elif label =='halfyear':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='06')]
return df.drop_duplicates('year-month').index
#获取股票池的组合收益(不进行市值加权)
def ret_se(sl,start_date='2018-6-1',end_date='2018-7-1',w=[1.0/len(sl)]*len(sl)):
if len(sl) != 0:
#得到股票的历史价格数据
df = get_price(list(sl),start_date=start_date,end_date=end_date,fields=['close']).close
df = df.dropna(axis=1)
#获取列表中的股票流通市值对数值
df_mkt = get_fundamentals(query(valuation.code,valuation.circulating_market_cap).filter(valuation.code.in_(df.columns)))
df_mkt.index = df_mkt['code'].values
fact_se =pd.Series(df_mkt['circulating_market_cap'].values,index = df_mkt['code'].values)
fact_se = np.log(fact_se)
else:
df = get_price('000001.XSHG',start_date=start_date,end_date=end_date,fields=['close'])
df['v'] = [1]*len(df)
del df['close']
#相当于昨天的百分比变化
pct = df.pct_change()+1
pct.iloc[0,:] = 1
#df1 = pct.cumprod()
#等权重平均收益结果
#按权重的方式计算
se1 = (pct*w).cumsum(axis=1).iloc[:,-1]
se2 = pct.cumsum(axis=1).iloc[:,-1]/pct.shape[1]
return se1,se2
def f_sum(x):
return sum(x)
#设置回测时间
start,end = '2016-9-1','2018-9-1'
#获取交易日列表
trade_list = get_tradeday_list(start,end,'month')
num = 1
for s,e in zip(trade_list[:-1],trade_list[1:]):
#获取满足条件的股票列表
pool = get_pool(s)
#获取优化权重
w = opt_func(pool,s)
if num == 0:
df_returns1 = ret_se(pool,s,e,w)[0]
df_a1 = ret_se(pool,s,e,w)[1]
df_returns = pd.concat([df_returns,df_returns1])
df_a = pd.concat([df_a,df_a1])
else:
df_returns = ret_se(pool,s,e,w)[0]
df_a = ret_se(pool,s,e,w)[1]
num = 0
#进行图表展示
df_returns.cumprod().plot(figsize=(12,7),legend=True,label='组合优化收益',title='图2 组合收益走势')
df_a.cumprod().plot(figsize=(12,7),legend=True,label='平均分仓收益')
<matplotlib.axes._subplots.AxesSubplot at 0x7f7a45724f90>
#计算总收益率
total_return1,total_return2 = df_returns.cumprod().values[-1]-1,df_a.cumprod().values[-1]-1
#计算年化收益
total_a_r1,total_a_r2 = (1+total_return1)**(250.0/len(df_returns))-1,(1+total_return2)**(250.0/len(df_a))-1
#计算夏普率
sharpe1,sharpe2 = (total_a_r1-0.04)/np.std(df_returns.cumprod()),(total_a_r2-0.04)/np.std(df_a.cumprod())
df_summary = pd.DataFrame([],index=['均值方差优化组合','平均分仓组合'])
df_summary['总收益'] = [total_return1,total_return2]
df_summary['年化收益'] = [total_a_r1,total_a_r2]
df_summary['sharpe'] = [sharpe1,sharpe2]
df_summary
| 总收益 | 年化收益 | sharpe | |
|---|---|---|---|
| 均值方差优化组合 | 0.106654 | 0.053288 | 0.056197 |
| 平均分仓组合 | -0.175383 | -0.094066 | -0.969469 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
