本篇是 价值低波(上)--因子加强的续篇。预告还有下集。
一般来说,三部曲的“上”比较精彩,“中”要打打酱油,补交作业,并且为“下”做铺垫。这儿,研究市盈率。
以下是根据历史数据回溯得到的沪深300的PE曲线,从2005-4-8到2019-3-30。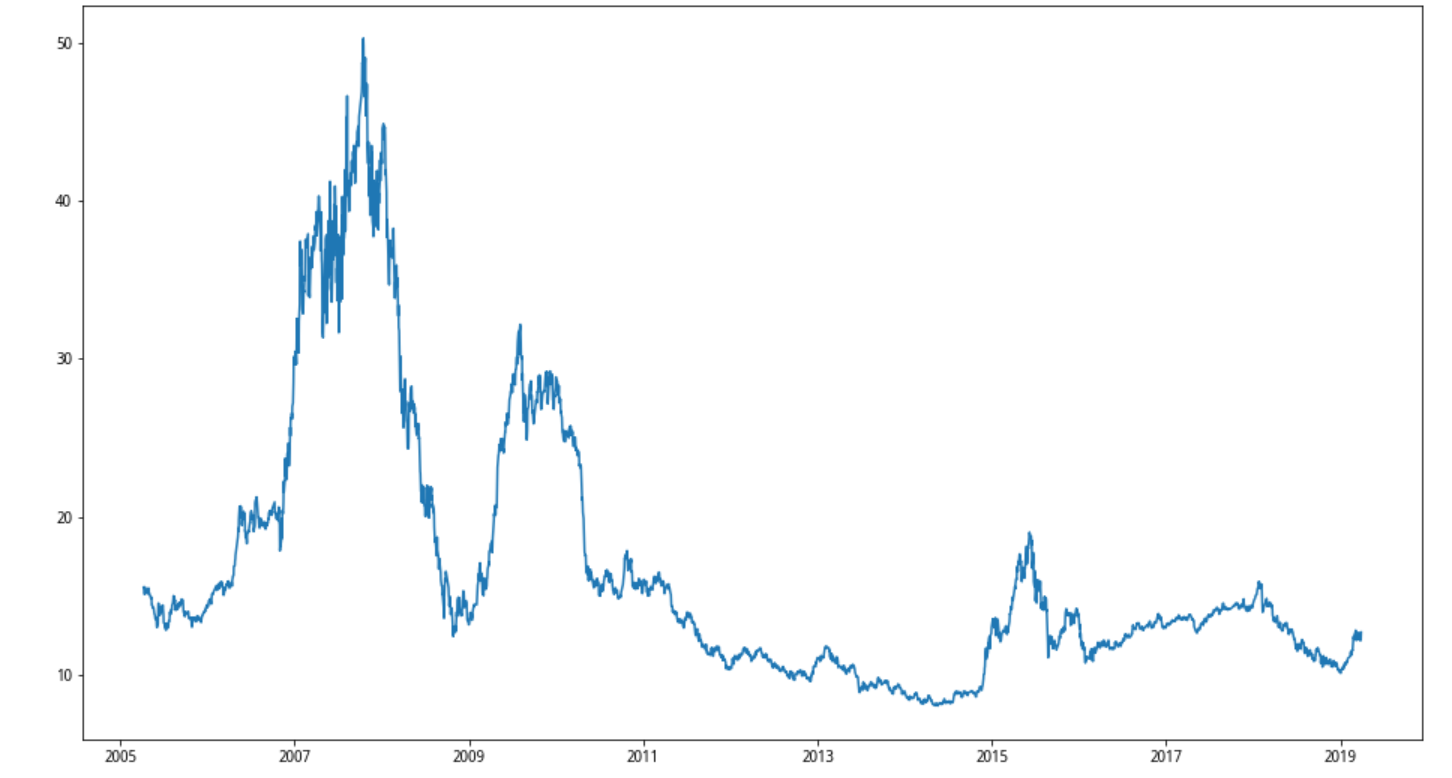
以下是沪深300的PE分布。
这是什么分布?什么概率分布都不是。咱也别去计算方差以及高阶统计信息了,没意思。
但是,有两个清晰的信息。左侧出现了明确的断崖,这就是说,价值投资是有道理的,当是市场跌到一定程度,它必然跌不下去了,在PE曲线图上即底部特征明显。右侧拉得很远,市场的疯狂程度不可限量,在P/E曲线上,2007、2010、2015三次牛市,高估的程度相差很大。
为了进一步探讨,我把价格曲线、P/E曲线归一化、对数化,绘制在一个图里边,然后手工画了一条横线: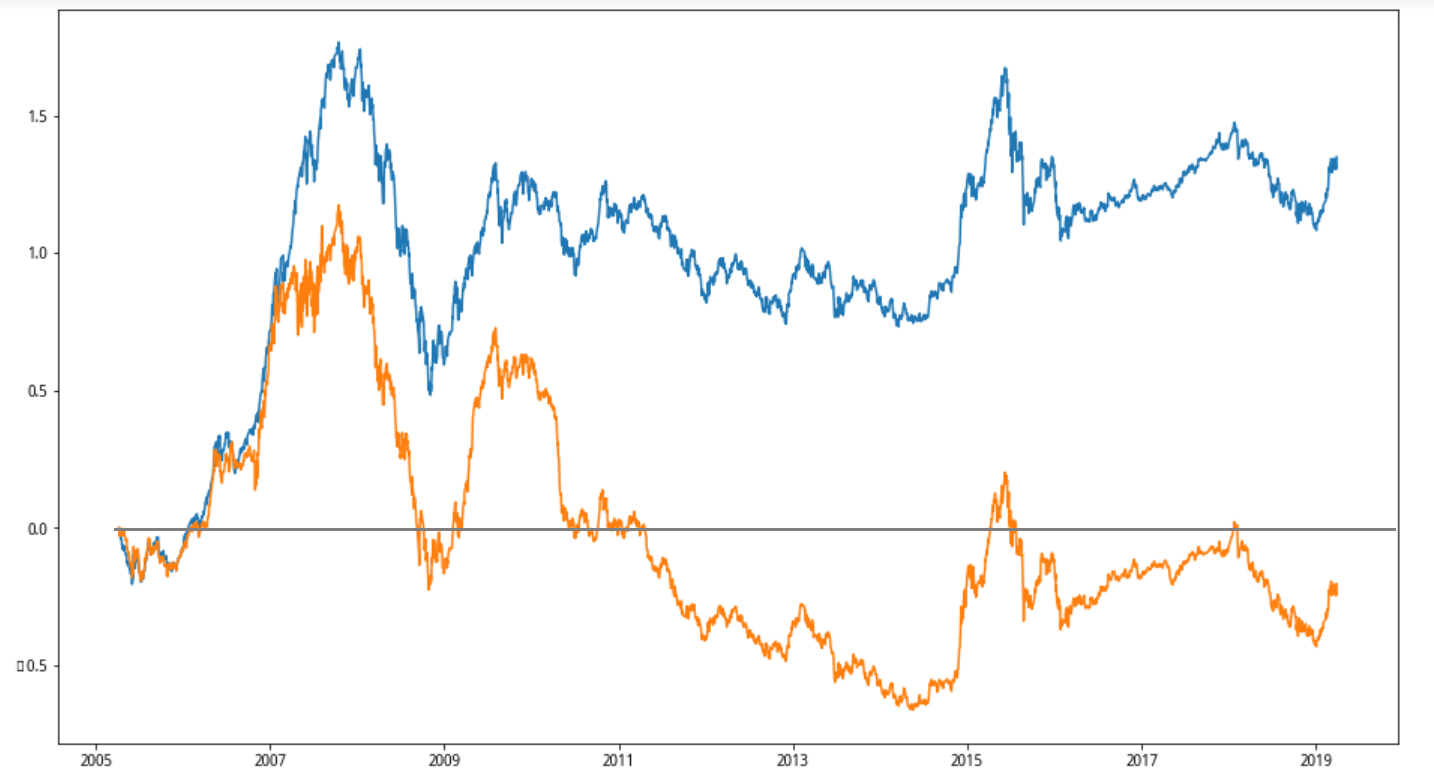
在对数图上,不但高点没规律,低点也没有。市场疯狂无可计算,市场的悲观也难以阻止。我们还是看一下统计数据吧: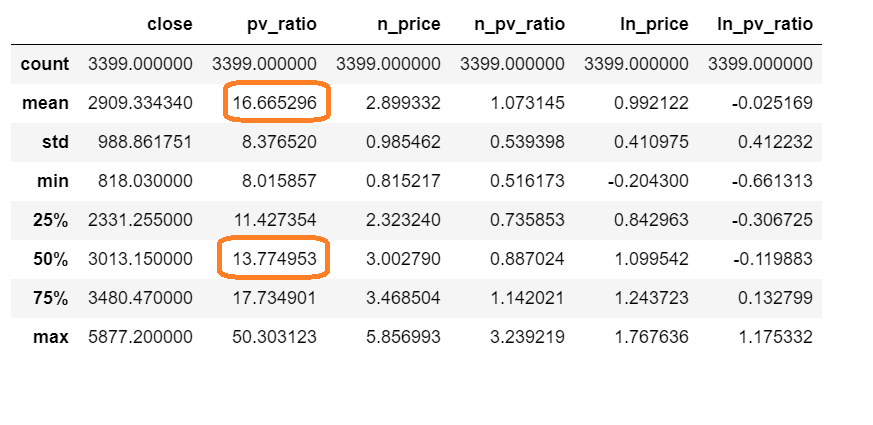
PE 的均值是16.66,中值13.77,于是,设计价值策略可以从PE=15划一刀,以上控制回撤,以下爱咋咋的,它又能咋地。
下面的系统是按以上思路设计的交易框架(强调,纯框架测试):
1 沪深300 P/E < 15,满仓上证50ETF。这只是一个测试。
2 沪深300 P/E > 30,80%国债指数、20% 上证50ETF。在回测环境下指数是可以交易的,为这个功能点赞,因为?早期没基金可以选啊。
我觉得这个结果很好。前些日子JQ组织探讨什么是好的交易系统,我说,达到目标的系统就是好系统。这个系统达到了我的目标。首先,它跑赢了沪深300。其次,它控制住了风险。第三,它非常简单。我要一个够硬的框架,它是那个框架。
OK,价值低波的基本元素有了,这就是 “价值低波(上)”。“上”留下了一些问题,解决问题需要一个新框架。现在框架也有了,这就是“价值低波(中)”。接下来是“下”了,价值低波搬入新框架,新楼老住户。
import numpy as np
import pandas as pd
import datetime as dt
import matplotlib
# 取得2005-4-8 ~ 2019-3-30 之间的所有的交易日
index = '000300.XSHG'
start_date = dt.date(2005, 4, 8)
end_date =dt.date(2019, 3, 30)
p = get_price(index, start_date, end_date, 'daily', ['close'])
p[:10]
| close | |
|---|---|
| 2005-04-08 | 1003.45 |
| 2005-04-11 | 995.42 |
| 2005-04-12 | 978.70 |
| 2005-04-13 | 1000.90 |
| 2005-04-14 | 986.98 |
| 2005-04-15 | 974.08 |
| 2005-04-18 | 963.77 |
| 2005-04-19 | 965.89 |
| 2005-04-20 | 950.87 |
| 2005-04-21 | 943.98 |
# 作图
plt.subplots(figsize=(16,9))
plot(p.close, 'b')
[<matplotlib.lines.Line2D at 0x7f5731229550>]
# 建立市场估值
mp = pd.Series([],[])
for d in p.index:
# 取得股票池
stocks = get_index_stocks(index, date=d)
# 基本面过滤
df = get_fundamentals(query(
valuation.code,
valuation.market_cap,
(valuation.market_cap/valuation.pe_ratio).label('value'),
).filter(
valuation.code.in_(list(stocks)),
), date=d).dropna()
market_value = df.market_cap.sum()/df.value.sum()
mp[d]= market_value
mp[:10]
# 作图
plt.subplots(figsize=(16, 9))
plot(mp)
# 直方图
pyplot.hist(mp, 100)
(array([ 91., 95., 107., 63., 62., 145., 119., 159., 171.,
108., 87., 157., 198., 203., 190., 108., 83., 122.,
130., 62., 44., 24., 21., 18., 18., 16., 22.,
37., 52., 24., 21., 16., 7., 6., 7., 7.,
3., 9., 21., 19., 25., 21., 17., 20., 22.,
27., 30., 23., 29., 17., 6., 5., 8., 4.,
4., 2., 9., 7., 3., 2., 10., 8., 9.,
12., 12., 7., 8., 11., 13., 14., 14., 13.,
10., 7., 6., 8., 12., 9., 13., 4., 6.,
9., 7., 5., 5., 6., 6., 1., 3., 0.,
0., 6., 1., 2., 2., 0., 3., 1., 2., 1.]),
array([ 8.01585711, 8.43872976, 8.86160242, 9.28447507,
9.70734773, 10.13022038, 10.55309304, 10.97596569,
11.39883835, 11.821711 , 12.24458366, 12.66745631,
13.09032896, 13.51320162, 13.93607427, 14.35894693,
14.78181958, 15.20469224, 15.62756489, 16.05043755,
16.4733102 , 16.89618286, 17.31905551, 17.74192817,
18.16480082, 18.58767348, 19.01054613, 19.43341879,
19.85629144, 20.27916409, 20.70203675, 21.1249094 ,
21.54778206, 21.97065471, 22.39352737, 22.81640002,
23.23927268, 23.66214533, 24.08501799, 24.50789064,
24.9307633 , 25.35363595, 25.77650861, 26.19938126,
26.62225391, 27.04512657, 27.46799922, 27.89087188,
28.31374453, 28.73661719, 29.15948984, 29.5823625 ,
30.00523515, 30.42810781, 30.85098046, 31.27385312,
31.69672577, 32.11959843, 32.54247108, 32.96534374,
33.38821639, 33.81108904, 34.2339617 , 34.65683435,
35.07970701, 35.50257966, 35.92545232, 36.34832497,
36.77119763, 37.19407028, 37.61694294, 38.03981559,
38.46268825, 38.8855609 , 39.30843356, 39.73130621,
40.15417887, 40.57705152, 40.99992417, 41.42279683,
41.84566948, 42.26854214, 42.69141479, 43.11428745,
43.5371601 , 43.96003276, 44.38290541, 44.80577807,
45.22865072, 45.65152338, 46.07439603, 46.49726869,
46.92014134, 47.34301399, 47.76588665, 48.1887593 ,
48.61163196, 49.03450461, 49.45737727, 49.88024992, 50.30312258]),
<a list of 100 Patch objects>)
# 把估值数据加入表格
p['pv_ratio'] = mp
p[:10]
| close | pv_ratio | |
|---|---|---|
| 2005-04-08 | 1003.45 | 15.529399 |
| 2005-04-11 | 995.42 | 15.430660 |
| 2005-04-12 | 978.70 | 15.069911 |
| 2005-04-13 | 1000.90 | 15.532478 |
| 2005-04-14 | 986.98 | 15.354481 |
| 2005-04-15 | 974.08 | 15.153486 |
| 2005-04-18 | 963.77 | 15.340893 |
| 2005-04-19 | 965.89 | 15.351643 |
| 2005-04-20 | 950.87 | 15.159701 |
| 2005-04-21 | 943.98 | 15.252221 |
# 归一化
p['n_price'] = p.close/p.close[0]
p['n_pv_ratio'] = p.pv_ratio/p.pv_ratio[0]
p[:10]
| close | pv_ratio | n_price | n_pv_ratio | |
|---|---|---|---|---|
| 2005-04-08 | 1003.45 | 15.529399 | 1.000000 | 1.000000 |
| 2005-04-11 | 995.42 | 15.430660 | 0.991998 | 0.993642 |
| 2005-04-12 | 978.70 | 15.069911 | 0.975335 | 0.970412 |
| 2005-04-13 | 1000.90 | 15.532478 | 0.997459 | 1.000198 |
| 2005-04-14 | 986.98 | 15.354481 | 0.983587 | 0.988736 |
| 2005-04-15 | 974.08 | 15.153486 | 0.970731 | 0.975793 |
| 2005-04-18 | 963.77 | 15.340893 | 0.960456 | 0.987861 |
| 2005-04-19 | 965.89 | 15.351643 | 0.962569 | 0.988554 |
| 2005-04-20 | 950.87 | 15.159701 | 0.947601 | 0.976194 |
| 2005-04-21 | 943.98 | 15.252221 | 0.940734 | 0.982151 |
# 对数化
p['ln_price'] = np.log(p.n_price)
p['ln_pv_ratio'] = np.log(p.n_pv_ratio)
p[:10]
| close | pv_ratio | n_price | n_pv_ratio | ln_price | ln_pv_ratio | |
|---|---|---|---|---|---|---|
| 2005-04-08 | 1003.45 | 15.529399 | 1.000000 | 1.000000 | 0.000000 | 0.000000 |
| 2005-04-11 | 995.42 | 15.430660 | 0.991998 | 0.993642 | -0.008035 | -0.006379 |
| 2005-04-12 | 978.70 | 15.069911 | 0.975335 | 0.970412 | -0.024974 | -0.030035 |
| 2005-04-13 | 1000.90 | 15.532478 | 0.997459 | 1.000198 | -0.002544 | 0.000198 |
| 2005-04-14 | 986.98 | 15.354481 | 0.983587 | 0.988736 | -0.016550 | -0.011328 |
| 2005-04-15 | 974.08 | 15.153486 | 0.970731 | 0.975793 | -0.029706 | -0.024504 |
| 2005-04-18 | 963.77 | 15.340893 | 0.960456 | 0.987861 | -0.040347 | -0.012213 |
| 2005-04-19 | 965.89 | 15.351643 | 0.962569 | 0.988554 | -0.038149 | -0.011512 |
| 2005-04-20 | 950.87 | 15.159701 | 0.947601 | 0.976194 | -0.053822 | -0.024094 |
| 2005-04-21 | 943.98 | 15.252221 | 0.940734 | 0.982151 | -0.061094 | -0.018010 |
# 作图
plt.subplots(figsize=(16,9))
plot(p[['ln_price', 'ln_pv_ratio']])
[<matplotlib.lines.Line2D at 0x7f843d3c9b50>, <matplotlib.lines.Line2D at 0x7f84263e1e10>]
# 统计特征
p.describe()
| close | pv_ratio | n_price | n_pv_ratio | ln_price | ln_pv_ratio | |
|---|---|---|---|---|---|---|
| count | 3399.000000 | 3399.000000 | 3399.000000 | 3399.000000 | 3399.000000 | 3399.000000 |
| mean | 2909.334340 | 16.665296 | 2.899332 | 1.073145 | 0.992122 | -0.025169 |
| std | 988.861751 | 8.376520 | 0.985462 | 0.539398 | 0.410975 | 0.412232 |
| min | 818.030000 | 8.015857 | 0.815217 | 0.516173 | -0.204300 | -0.661313 |
| 25% | 2331.255000 | 11.427354 | 2.323240 | 0.735853 | 0.842963 | -0.306725 |
| 50% | 3013.150000 | 13.774953 | 3.002790 | 0.887024 | 1.099542 | -0.119883 |
| 75% | 3480.470000 | 17.734901 | 3.468504 | 1.142021 | 1.243723 | 0.132799 |
| max | 5877.200000 | 50.303123 | 5.856993 | 3.239219 | 1.767636 | 1.175332 |
from jqdata import finance
q = query(finance.STK_EXCHANGE_TRADE_INFO.exchange_name, \
finance.STK_EXCHANGE_TRADE_INFO.pe_average,\
finance.STK_EXCHANGE_TRADE_INFO.date)\
.filter(finance.STK_EXCHANGE_TRADE_INFO.date=='2019-04-12')
f = finance.run_query(q)
f
| exchange_name | pe_average | date | |
|---|---|---|---|
| 0 | 上海A股 | 15.990 | 2019-04-12 |
| 1 | 上海B股 | 12.284 | 2019-04-12 |
| 2 | 上海市场 | 15.977 | 2019-04-12 |
| 3 | 中小企业板 | 28.800 | 2019-04-12 |
| 4 | 深市主板 | 18.690 | 2019-04-12 |
| 5 | 深圳市场 | 26.040 | 2019-04-12 |
| 6 | 创业板 | 41.970 | 2019-04-12 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...