请　[注册]　或　[登录]　 | 返回主站

量化交易吧 /  量化平台 帖子：3365818 新帖：25

可转债期权的初步研究疑问

Tango发表于：5 月 10 日 03：54回复(1)

方法一：百分比价格变动法(即价格的环比增长速度)。
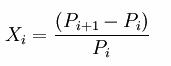
242424.jpg

(1)式中，Xi是资产的百分比收益，Pi是昨天(基期)资产的价格，Pi 1是今天(报告期)资产的价格。

方法二：对数价格变动法。
两个公式的假定不一样，百分比收益公式假定有固定的不连续间隔价格变化，而对数收益公式假定价格是连续的变化。在Black-Scholes模型中，假定价格变动是连续的，可从连续利率因子e ? RT将敲定价格换算成现值这一事实推导得出。所以，对于这个模型，对数收益公式是确定波动率的合适公式。针对资产的对数收益求其平均数\bar{x}，然后根据下面公式得到历史波动率的估计值。
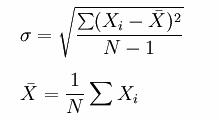
2424242424.jpg
N是观察值的数量， σ代表对数收益的平均离差，即标准差。若将日、周等标准差转化为年标准差，需要乘以以年为单位的频数长度的平方根

可转债正股历史1年的波动率如图所示进行计算

之后代入BS公式中计算可转债的期权价值

纯债价值 期权价值 = 可转债理论价值

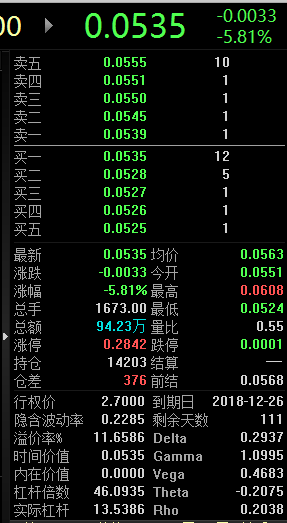
234.png

用bs验证下正确性

但得到的期权价格与真实不符合 望大神答疑

import jqdata
import copy
import numpy as np
import pandas as pd
import random as ran
from datetime import datetime,timedelta
import sklearn
import talib as tl
import math
import scipy

import math
#泰康转债 泰康生物为例

#波动率计算为0.6454091024794429
#BS模型:

from math import log,sqrt,exp
from scipy.stats import norm
def call_option_pricer(spot,strike,maturity,r,vol):
    d1=(log(spot/strike)+(r+0.5*vol*vol)*maturity)/vol/sqrt(maturity)
    d2=d1-vol*sqrt(maturity)
    price=spot*norm.cdf(d1)-strike*exp(-r*maturity)*norm.cdf(d2)
    return price
print('50etf购12月2700期权价格:%.4f'%call_option_pricer(spot=2.466,strike=2.7,maturity=111/365,r=0.044,vol=0.2285))

#当前价 spot : 2.466
#行权价 strike : 2.7
#到期期限 maturity : 111/365
#无风险利率 r : 0.044
#波动率 vol : 0.2285
#0.058

50etf购12月2700期权价格:0.0533

#与真实价格0.0535 相差0.0002

#用此函数计算可初步估算转债期权价格

#123008	康泰转债	140.000	2.84%	康泰生物	43.50	1.87%	19.30	31.230	139.289	0.51%	75.71	39.82	115.53	17.48%	61.03%	50.26%	40.60	1.6%	24.24%	24-02-01	5.408	-4.26%	-4.61%	22-05-02	3.65	-7.94%	-8.11%	14310.26	0.00

print('泰康可转债期权价格:%.4f'%call_option_pricer(spot=43.50,strike=31.230,maturity=5.41,r=0.044,vol=0.6103))

泰康可转债期权价格:28.3771

#所以泰康转债估算理论价值 具体的算法更为复杂 后续讨论

print('value',28.3771+75.71)

value 104.08709999999999

       

全部回复

0/140

量化课程

    移动端课程