一、摘要
本报告基于传统的指数RSRS(阻力支撑相对强弱)择时进行了拓展,尝试了基于申万一二级行业的行业指数RSRS择时效果。本文所选的行业均为热门且关注度较高的行业。由于行业指数不可交易,因此在交易时买卖的是该行业市值最大的十支股票,以此来作为交易行业指数的代理变量。结果发现,在我们测试的申万一二级行业中,801150 医药生物I的择时效果最差,择时跑不赢简单的买入持有指数的累计收益;801050 有色金属I的择时效果最好,择时的净值是简单的买入持有指数净值的3.71倍。进一步研究发现,择时结合买入该行业低估值的股票效果喜人,策略在所有行业均有增强效果,801050 有色金属I的效果最佳,净值倍数达到了12.24。
二、理论发展与指标描述
2.1 阻力支撑相对强弱(RSRS)
关于RSRS(阻力支撑相对强弱)指标的介绍,可以参考聚宽量化课堂的文章《【量化课堂】RSRS(阻力支撑相对强度)择时策略(上)》
三、数据和策略
3.1 数据
本文的行业指数数据来自申万行业数据、聚宽行业概念数据库和大智慧,值得注意的是,我们挑选的是几个比较有代表性、数据比较齐全的行业。测试的行业列表如下:
针对上述行业,我们测试了两种策略。分别为大市值与低估值。大市值策略的理论基础是大市值股票占据了该行业所有股票市值之和的 90%以上,可以很好地作为该行业的代理。低估值策略的理论基础是低估值股票具有较高的升值空间,应该具有较强的超额收益。这两种策略的具体逻辑如下: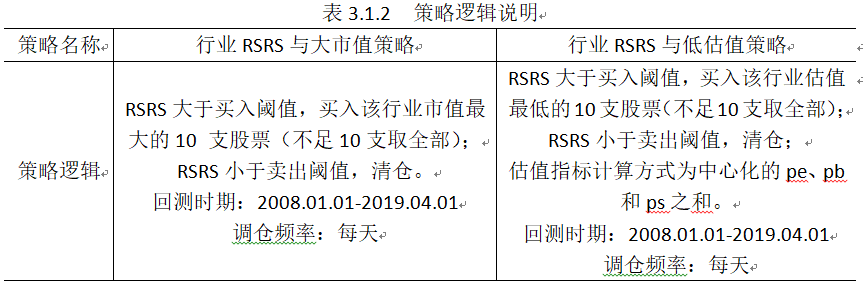
四、测试结果
表4.1与图4.1列示了行业RSRS与大市值策略的测试结果。
表4.1
图4.1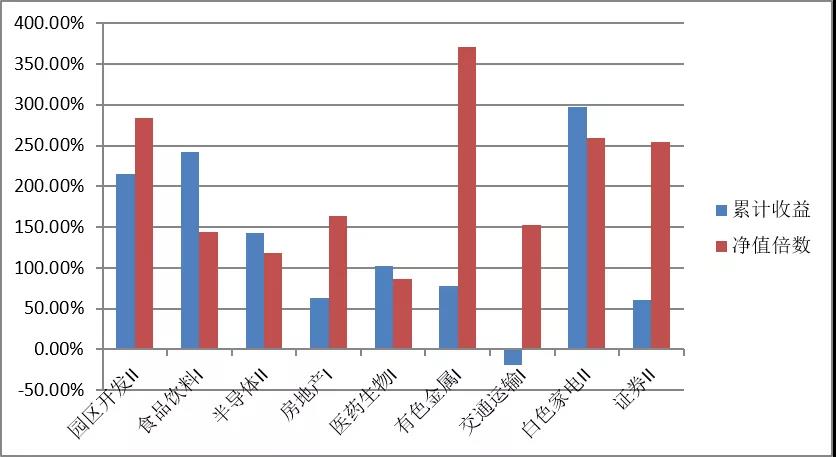
从表 4.1 和图 4.1 中可以看出,累计收益最高的是白色家电II行业,但由于该行业指数的累计收益本身就比较高,因此净值倍数并不是最好的。净值倍数最大的是有色金属 I 行业,由于该行业指数的累计收益非常低,所以即便 RSRS 择时的效果不是最突出的,但也极大地提升了净值倍数。净值倍数小于 1 的行业有医药生物 I,这说明该行业择时的效果还不如简单地买入持有。综上所述,有色金属 I 行业最适合 RSRS 择时,医药生物I行业最不适合 RSRS 择时,园区开发 II 和白色家电 II 在累计收益层面和净值倍数层面两开花。
图 4.2 至图 4.5 列示了有色金属 I、医药生物 I、园区开发 II 和白色家电 II 在大市值策略下的资金曲线。
进一步地,我们测试了低估值策略的效果。表 4.2 与图 4.6 列示了行业 RSRS 与低估值策略的测试结果。
表4.2
图4.6
从表 4.2 和图 4.6 中可以看出,累计收益最高的是有色金属I行业,达到了 487.61%。净值倍数最高的也是有色金属 I 行业,达到了惊人的 12 倍之多。医药生物 I 依旧表现较差,净值倍数尽管超过了 1,但仍是几个行业中排名靠后的,除此之外,食品饮料的累计收益与净值倍数均非常差。交通运输 I 的累计收益很低,但由于该行业指数的表现较差,因此净值提升是第二高的,超过了 4 倍,仅次于有色金属。综上所述,在低估值选股策略下,有色金属 I 行业收益净值两开花,食品饮料 I 与医药生物 I 堪称难兄难弟,白色家电 II 依旧表现优秀。
图 4.7 至图 4.10 列示了有色金属 I、食品饮料 I、医药生物 I 与白色家电 II 在低估值策略下的资金曲线。
五、结论
在可以代表行业指数的大市值策略下,有色金属I行业最适合RSRS择时,医药生物I行业最不适合RSRS择时,园区开发II和白色家电II的择时效果在累计收益层面和净值倍数层面两开花。有色金属I适合择时的原因在于指数收益较低,择时提升幅度大;医药生物I不适合择时的原因在于指数收益较高,择时难以跑赢指数。
在低估值策略下,有色金属I行业最适合RSRS择时,食品饮料I与医药生物I虽然堪称难兄难弟,但择时也可以小幅度提升绩效,但显然,绩效的提升是低估值因子带来的,白色家电II依旧表现优秀,累计收益与净值倍数两开花。有色金属I适合择时的原因在于指数收益较低,择时提升幅度大;食品饮料I与医药生物I不适合择时的原因在于择时难以大幅度跑赢指数。
综上所述,涨幅较大,且回撤较小的指数,难以择时。非周期性行业(消费、医药)难以择时,周期性行业(有色)容易择时。其他结论有待进一步明确。
注:本文所使用的行业指数数据已上传至百度云网盘,
提取码:e27y
研究平台调用回测的方法参考聚宽量化课堂《【量化课堂】多回测运行和参数分析框架》,
#1 先导入所需要的程序包import datetimeimport numpy as npimport pandas as pdimport timefrom jqdata import *from pandas import Series, DataFrameimport matplotlib.pyplot as pltimport seaborn as snsimport itertoolsimport copyimport pickle# 定义类'参数分析'class parameter_analysis(object):# 定义函数中不同的变量def __init__(self, algorithm_id=None):self.algorithm_id = algorithm_id # 回测idself.params_df = pd.DataFrame() # 回测中所有调参备选值的内容,列名字为对应修改面两名称,对应回测中的 g.XXXXself.results = {} # 回测结果的回报率,key 为 params_df 的行序号,value 为self.evaluations = {} # 回测结果的各项指标,key 为 params_df 的行序号,value 为一个 dataframeself.backtest_ids = {} # 回测结果的 id# 新加入的基准的回测结果 id,可以默认为空 '',则使用回测中设定的基准self.benchmark_id = 'f16629492d6b6f4040b2546262782c78'
self.benchmark_returns = [] # 新加入的基准的回测回报率self.returns = {} # 记录所有回报率self.excess_returns = {} # 记录超额收益率self.log_returns = {} # 记录收益率的 log 值self.log_excess_returns = {} # 记录超额收益的 log 值self.dates = [] # 回测对应的所有日期self.excess_max_drawdown = {} # 计算超额收益的最大回撤self.excess_annual_return = {} # 计算超额收益率的年化指标self.evaluations_df = pd.DataFrame() # 记录各项回测指标,除日回报率外# 定义排队运行多参数回测函数def run_backtest(self, # algorithm_id=None, # 回测策略id running_max=10, # 回测中同时巡行最大回测数量 start_date='2006-01-01', # 回测的起始日期 end_date='2016-11-30', # 回测的结束日期 frequency='day', # 回测的运行频率 initial_cash='1000000', # 回测的初始持仓金额 param_names=[], # 回测中调整参数涉及的变量 param_values=[] # 回测中每个变量的备选参数值 ):# 当此处回测策略的 id 没有给出时,调用类输入的策略 idif algorithm_id == None: algorithm_id=self.algorithm_id# 生成所有参数组合并加载到 df 中# 包含了不同参数具体备选值的排列组合中一组参数的 tuple 的 listparam_combinations = list(itertools.product(*param_values))# 生成一个 dataframe, 对应的列为每个调参的变量,每个值为调参对应的备选值to_run_df = pd.DataFrame(param_combinations)# 修改列名称为调参变量的名字to_run_df.columns = param_names# 设定运行起始时间和保存格式start = time.time()# 记录结束的运行回测finished_backtests = {}# 记录运行中的回测running_backtests = {}# 计数器pointer = 0# 总运行回测数目,等于排列组合中的元素个数total_backtest_num = len(param_combinations)# 记录回测结果的回报率all_results = {}# 记录回测结果的各项指标all_evaluations = {}# 在运行开始时显示print('【已完成|运行中|待运行】:')# 当运行回测开始后,如果没有全部运行完全的话:while len(finished_backtests)<total_backtest_num:# 显示运行、完成和待运行的回测个数print('[%s|%s|%s].' % (len(finished_backtests),
len(running_backtests),
(total_backtest_num-len(finished_backtests)-len(running_backtests)) ))# 记录当前运行中的空位数量to_run = min(running_max-len(running_backtests), total_backtest_num-len(running_backtests)-len(finished_backtests))# 把可用的空位进行跑回测for i in range(pointer, pointer+to_run):# 备选的参数排列组合的 df 中第 i 行变成 dict,每个 key 为列名字,value 为 df 中对应的值params = to_run_df.ix[i].to_dict()# 记录策略回测结果的 id,调整参数 extras 使用 params 的内容backtest = create_backtest(algorithm_id = algorithm_id, start_date = start_date,
end_date = end_date,
frequency = frequency,
initial_cash = initial_cash,
extras = params,
# 再回测中把改参数的结果起一个名字,包含了所有涉及的变量参数值 name = str(params) )# 记录运行中 i 回测的回测 idrunning_backtests[i] = backtest# 计数器计数运行完的数量 pointer = pointer+to_run# 获取回测结果failed = []finished = []# 对于运行中的回测,key 为 to_run_df 中所有排列组合中的序数for key in running_backtests.keys():# 研究调用回测的结果,running_backtests[key] 为运行中保存的结果 idbt = get_backtest(running_backtests[key])# 获得运行回测结果的状态,成功和失败都需要运行结束后返回,如果没有返回则运行没有结束status = bt.get_status()# 当运行回测失败if status == 'failed':# 失败 list 中记录对应的回测结果 idfailed.append(key)# 当运行回测成功时elif status == 'done':# 成功 list 记录对应的回测结果 id,finish 仅记录运行成功的finished.append(key)# 回测回报率记录对应回测的回报率 dict, key to_run_df 中所有排列组合中的序数, value 为回报率的 dict# 每个 value 一个 list 每个对象为一个包含时间、日回报率和基准回报率的 dictall_results[key] = bt.get_results()# 回测回报率记录对应回测结果指标 dict, key to_run_df 中所有排列组合中的序数, value 为回测结果指标的 dataframeall_evaluations[key] = bt.get_risk()# 记录运行中回测结果 id 的 list 中删除失败的运行for key in failed:running_backtests.pop(key)# 在结束回测结果 dict 中记录运行成功的回测结果 id,同时在运行中的记录中删除该回测for key in finished:finished_backtests[key] = running_backtests.pop(key)# 当一组同时运行的回测结束时报告时间if len(finished_backtests) != 0 and len(finished_backtests) % running_max == 0 and to_run !=0:# 记录当时时间middle = time.time()# 计算剩余时间,假设没工作量时间相等的话remain_time = (middle - start) * (total_backtest_num - len(finished_backtests)) / len(finished_backtests)# print 当前运行时间print('[已用%s时,尚余%s时,请不要关闭浏览器].' % (str(round((middle - start) / 60.0 / 60.0,3)),
str(round(remain_time / 60.0 / 60.0,3)))),# 5秒钟后再跑一下time.sleep(5) # 记录结束时间end = time.time() print('')print('【回测完成】总用时:%s秒(即%s小时)。' % (str(int(end-start)),
str(round((end-start)/60.0/60.0,2)))),# 对应修改类内部对应self.params_df = to_run_dfself.results = all_resultsself.evaluations = all_evaluationsself.backtest_ids = finished_backtests#7 最大回撤计算方法def find_max_drawdown(self, returns):# 定义最大回撤的变量result = 0# 记录最高的回报率点historical_return = 0# 遍历所有日期for i in range(len(returns)):# 最高回报率记录historical_return = max(historical_return, returns[i])# 最大回撤记录drawdown = 1-(returns[i] + 1) / (historical_return + 1)# 记录最大回撤result = max(drawdown, result)# 返回最大回撤值return result# log 收益、新基准下超额收益和相对与新基准的最大回撤def organize_backtest_results(self, benchmark_id=None):# 若新基准的回测结果 id 没给出if benchmark_id==None:# 使用默认的基准回报率,默认的基准在回测策略中设定self.benchmark_returns = [x['benchmark_returns'] for x in self.results[0]]# 当新基准指标给出后 else:# 基准使用新加入的基准回测结果self.benchmark_returns = [x['returns'] for x in get_backtest(benchmark_id).get_results()]# 回测日期为结果中记录的第一项对应的日期self.dates = [x['time'] for x in self.results[0]]# 对应每个回测在所有备选回测中的顺序 (key),生成新数据# 由 {key:{u'benchmark_returns': 0.022480100091729405,# u'returns': 0.03184566700000002,# u'time': u'2006-02-14'}} 格式转化为:# {key: []} 格式,其中 list 为对应 date 的一个回报率 listfor key in self.results.keys():self.returns[key] = [x['returns'] for x in self.results[key]]# 生成对于基准(或新基准)的超额收益率for key in self.results.keys():self.excess_returns[key] = [(x+1)/(y+1)-1 for (x,y) in zip(self.returns[key], self.benchmark_returns)]# 生成 log 形式的收益率for key in self.results.keys():self.log_returns[key] = [log(x+1) for x in self.returns[key]]# 生成超额收益率的 log 形式for key in self.results.keys():self.log_excess_returns[key] = [log(x+1) for x in self.excess_returns[key]]# 生成超额收益率的最大回撤for key in self.results.keys():self.excess_max_drawdown[key] = self.find_max_drawdown(self.excess_returns[key])# 生成年化超额收益率for key in self.results.keys():self.excess_annual_return[key] = (self.excess_returns[key][-1]+1)**(252./float(len(self.dates)))-1# 把调参数据中的参数组合 df 与对应结果的 df 进行合并self.evaluations_df = pd.concat([self.params_df, pd.DataFrame(self.evaluations).T], axis=1)# self.evaluations_df = # 获取最总分析数据,调用排队回测函数和数据整理的函数 def get_backtest_data(self, algorithm_id=None, # 回测策略id benchmark_id=None, # 新基准回测结果id file_name='results.pkl', # 保存结果的 pickle 文件名字 running_max=10, # 最大同时运行回测数量 start_date='2006-01-01', # 回测开始时间 end_date='2016-11-30', # 回测结束日期 frequency='day', # 回测的运行频率 initial_cash='1000000', # 回测初始持仓资金 param_names=[], # 回测需要测试的变量 param_values=[] # 对应每个变量的备选参数 ):# 调运排队回测函数,传递对应参数self.run_backtest(algorithm_id=algorithm_id, running_max=running_max, start_date=start_date, end_date=end_date, frequency=frequency, initial_cash=initial_cash, param_names=param_names, param_values=param_values )# 回测结果指标中加入 log 收益率和超额收益率等指标self.organize_backtest_results(benchmark_id)# 生成 dict 保存所有结果。results = {'returns':self.returns, 'excess_returns':self.excess_returns, 'log_returns':self.log_returns, 'log_excess_returns':self.log_excess_returns, 'dates':self.dates, 'benchmark_returns':self.benchmark_returns, 'evaluations':self.evaluations, 'params_df':self.params_df, 'backtest_ids':self.backtest_ids, 'excess_max_drawdown':self.excess_max_drawdown, 'excess_annual_return':self.excess_annual_return, 'evaluations_df':self.evaluations_df}# 保存 pickle 文件pickle_file = open(file_name, 'wb')pickle.dump(results, pickle_file)pickle_file.close()# 读取保存的 pickle 文件,赋予类中的对象名对应的保存内容 def read_backtest_data(self, file_name='results.pkl'):pickle_file = open(file_name, 'rb')results = pickle.load(pickle_file)self.params_df = results['params_df']self.returns = results['returns']self.excess_returns = results['excess_returns']self.log_returns = results['log_returns']self.log_excess_returns = results['log_excess_returns']self.dates = results['dates']self.benchmark_returns = results['benchmark_returns']self.evaluations = results['evaluations']self.backtest_ids = results['backtest_ids']self.excess_max_drawdown = results['excess_max_drawdown']self.excess_annual_return = results['excess_annual_return']self.evaluations_df = results['evaluations_df']# 返回累计收益数据return(pd.DataFrame(self.returns),self.params_df,self.benchmark_returns)# 回报率折线图 def plot_returns(self):# 通过figsize参数可以指定绘图对象的宽度和高度,单位为英寸;fig = plt.figure(figsize=(20,8))ax = fig.add_subplot(111)# 作图for key in self.returns.keys():ax.plot(range(len(self.returns[key])), self.returns[key], label=key)# 设定benchmark曲线并标记ax.plot(range(len(self.benchmark_returns)), self.benchmark_returns, label='benchmark', c='k', linestyle='') ticks = [int(x) for x in np.linspace(0, len(self.dates)-1, 11)]plt.xticks(ticks, [self.dates[i] for i in ticks])# 设置图例样式ax.legend(loc = 2, fontsize = 10)# 设置y标签样式ax.set_ylabel('returns',fontsize=20)# 设置x标签样式ax.set_yticklabels([str(x*100)+'% 'for x in ax.get_yticks()])# 设置图片标题样式ax.set_title("Strategy's performances with different parameters", fontsize=21)plt.xlim(0, len(self.returns[0]))# 超额收益率图 def plot_excess_returns(self):# 通过figsize参数可以指定绘图对象的宽度和高度,单位为英寸;fig = plt.figure(figsize=(20,8))ax = fig.add_subplot(111)# 作图for key in self.returns.keys():ax.plot(range(len(self.excess_returns[key])), self.excess_returns[key], label=key)# 设定benchmark曲线并标记ax.plot(range(len(self.benchmark_returns)), [0]*len(self.benchmark_returns), label='benchmark', c='k', linestyle='')ticks = [int(x) for x in np.linspace(0, len(self.dates)-1, 11)]plt.xticks(ticks, [self.dates[i] for i in ticks])# 设置图例样式ax.legend(loc = 2, fontsize = 10)# 设置y标签样式ax.set_ylabel('excess returns',fontsize=20)# 设置x标签样式ax.set_yticklabels([str(x*100)+'% 'for x in ax.get_yticks()])# 设置图片标题样式ax.set_title("Strategy's performances with different parameters", fontsize=21)plt.xlim(0, len(self.excess_returns[0]))# log回报率图 def plot_log_returns(self):# 通过figsize参数可以指定绘图对象的宽度和高度,单位为英寸;fig = plt.figure(figsize=(20,8))ax = fig.add_subplot(111)# 作图for key in self.returns.keys():ax.plot(range(len(self.log_returns[key])), self.log_returns[key], label=key)# 设定benchmark曲线并标记ax.plot(range(len(self.benchmark_returns)), [log(x+1) for x in self.benchmark_returns], label='benchmark', c='k', linestyle='')ticks = [int(x) for x in np.linspace(0, len(self.dates)-1, 11)]plt.xticks(ticks, [self.dates[i] for i in ticks])# 设置图例样式ax.legend(loc = 2, fontsize = 10)# 设置y标签样式ax.set_ylabel('log returns',fontsize=20)# 设置图片标题样式ax.set_title("Strategy's performances with different parameters", fontsize=21)plt.xlim(0, len(self.log_returns[0]))# 超额收益率的 log 图def plot_log_excess_returns(self):# 通过figsize参数可以指定绘图对象的宽度和高度,单位为英寸;fig = plt.figure(figsize=(20,8))ax = fig.add_subplot(111)# 作图for key in self.returns.keys():ax.plot(range(len(self.log_excess_returns[key])), self.log_excess_returns[key], label=key)# 设定benchmark曲线并标记ax.plot(range(len(self.benchmark_returns)), [0]*len(self.benchmark_returns), label='benchmark', c='k', linestyle='')ticks = [int(x) for x in np.linspace(0, len(self.dates)-1, 11)]plt.xticks(ticks, [self.dates[i] for i in ticks])# 设置图例样式ax.legend(loc = 2, fontsize = 10)# 设置y标签样式ax.set_ylabel('log excess returns',fontsize=20)# 设置图片标题样式ax.set_title("Strategy's performances with different parameters", fontsize=21)plt.xlim(0, len(self.log_excess_returns[0]))# 回测的4个主要指标,包括总回报率、最大回撤夏普率和波动def get_eval4_bar(self, sort_by=[]):
sorted_params = self.params_dffor by in sort_by:sorted_params = sorted_params.sort(by)indices = sorted_params.indexfig = plt.figure(figsize=(20,7))# 定义位置ax1 = fig.add_subplot(221)# 设定横轴为对应分位,纵轴为对应指标ax1.bar(range(len(indices)), [self.evaluations[x]['algorithm_return'] for x in indices], 0.6, label = 'Algorithm_return')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax1.legend(loc='best',fontsize=15)# 设置y标签样式ax1.set_ylabel('Algorithm_return', fontsize=15)# 设置y标签样式ax1.set_yticklabels([str(x*100)+'% 'for x in ax1.get_yticks()])# 设置图片标题样式ax1.set_title("Strategy's of Algorithm_return performances of different quantile", fontsize=15)# x轴范围plt.xlim(0, len(indices))# 定义位置ax2 = fig.add_subplot(224)# 设定横轴为对应分位,纵轴为对应指标ax2.bar(range(len(indices)), [self.evaluations[x]['max_drawdown'] for x in indices], 0.6, label = 'Max_drawdown')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax2.legend(loc='best',fontsize=15)# 设置y标签样式ax2.set_ylabel('Max_drawdown', fontsize=15)# 设置x标签样式ax2.set_yticklabels([str(x*100)+'% 'for x in ax2.get_yticks()])# 设置图片标题样式ax2.set_title("Strategy's of Max_drawdown performances of different quantile", fontsize=15)# x轴范围plt.xlim(0, len(indices))# 定义位置ax3 = fig.add_subplot(223)# 设定横轴为对应分位,纵轴为对应指标ax3.bar(range(len(indices)),[self.evaluations[x]['sharpe'] for x in indices], 0.6, label = 'Sharpe')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax3.legend(loc='best',fontsize=15)# 设置y标签样式ax3.set_ylabel('Sharpe', fontsize=15)# 设置x标签样式ax3.set_yticklabels([str(x*100)+'% 'for x in ax3.get_yticks()])# 设置图片标题样式ax3.set_title("Strategy's of Sharpe performances of different quantile", fontsize=15)# x轴范围plt.xlim(0, len(indices))# 定义位置ax4 = fig.add_subplot(222)# 设定横轴为对应分位,纵轴为对应指标ax4.bar(range(len(indices)), [self.evaluations[x]['algorithm_volatility'] for x in indices], 0.6, label = 'Algorithm_volatility')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax4.legend(loc='best',fontsize=15)# 设置y标签样式ax4.set_ylabel('Algorithm_volatility', fontsize=15)# 设置x标签样式ax4.set_yticklabels([str(x*100)+'% 'for x in ax4.get_yticks()])# 设置图片标题样式ax4.set_title("Strategy's of Algorithm_volatility performances of different quantile", fontsize=15)# x轴范围plt.xlim(0, len(indices))#14 年化回报和最大回撤,正负双色表示def get_eval(self, sort_by=[]):sorted_params = self.params_dffor by in sort_by:sorted_params = sorted_params.sort(by)indices = sorted_params.index# 大小fig = plt.figure(figsize = (20, 8))# 图1位置ax = fig.add_subplot(111)# 生成图超额收益率的最大回撤ax.bar([x+0.3 for x in range(len(indices))], [-self.evaluations[x]['max_drawdown'] for x in indices], color = '#32CD32',
width = 0.6, label = 'Max_drawdown', zorder=10)# 图年化超额收益ax.bar([x for x in range(len(indices))], [self.evaluations[x]['annual_algo_return'] for x in indices], color = 'r',
width = 0.6, label = 'Annual_return')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax.legend(loc='best',fontsize=15)# 基准线plt.plot([0, len(indices)], [0, 0], c='k',
linestyle='', label='zero')# 设置图例样式ax.legend(loc='best',fontsize=15)# 设置y标签样式ax.set_ylabel('Max_drawdown', fontsize=15)# 设置x标签样式ax.set_yticklabels([str(x*100)+'% 'for x in ax.get_yticks()])# 设置图片标题样式ax.set_title("Strategy's performances of different quantile", fontsize=15)# 设定x轴长度plt.xlim(0, len(indices))#14 超额收益的年化回报和最大回撤# 加入新的benchmark后超额收益和def get_excess_eval(self, sort_by=[]):sorted_params = self.params_dffor by in sort_by:sorted_params = sorted_params.sort(by)indices = sorted_params.index# 大小fig = plt.figure(figsize = (20, 8))# 图1位置ax = fig.add_subplot(111)# 生成图超额收益率的最大回撤ax.bar([x+0.3 for x in range(len(indices))], [-self.excess_max_drawdown[x] for x in indices], color = '#32CD32',
width = 0.6, label = 'Excess_max_drawdown')# 图年化超额收益ax.bar([x for x in range(len(indices))], [self.excess_annual_return[x] for x in indices], color = 'r',
width = 0.6, label = 'Excess_annual_return')plt.xticks([x+0.3 for x in range(len(indices))], indices)# 设置图例样式ax.legend(loc='best',fontsize=15)# 基准线plt.plot([0, len(indices)], [0, 0], c='k',
linestyle='', label='zero')# 设置图例样式ax.legend(loc='best',fontsize=15)# 设置y标签样式ax.set_ylabel('Max_drawdown', fontsize=15)# 设置x标签样式ax.set_yticklabels([str(x*100)+'% 'for x in ax.get_yticks()])# 设置图片标题样式ax.set_title("Strategy's performances of different quantile", fontsize=15)# 设定x轴长度plt.xlim(0, len(indices))#2 设定回测策略 id pa = parameter_analysis('c3382da156d948253cb8ffc02f579a89')#3 运行回测pa.get_backtest_data(file_name = 'results.pkl', running_max = 50, benchmark_id = None, start_date = '2009-01-01', end_date = '2019-04-01', frequency = 'day', initial_cash = '5000000', param_names = ['RSRS_index'], param_values = ['801193','801017','801111','801170','801770','801750','801760','801050','801150','801180','801081','801120','801182','801741'] )
#4 回测参数的 Dataframepa.params_df
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
| buy | sell | |
|---|---|---|
| 0 | 0.5 | -0.5 |
| 1 | 0.5 | -0.6 |
| 2 | 0.5 | -0.7 |
| 3 | 0.5 | -0.8 |
| 4 | 0.5 | -0.9 |
| 5 | 0.6 | -0.5 |
| 6 | 0.6 | -0.6 |
| 7 | 0.6 | -0.7 |
| 8 | 0.6 | -0.8 |
| 9 | 0.6 | -0.9 |
| 10 | 0.7 | -0.5 |
| 11 | 0.7 | -0.6 |
| 12 | 0.7 | -0.7 |
| 13 | 0.7 | -0.8 |
| 14 | 0.7 | -0.9 |
| 15 | 0.8 | -0.5 |
| 16 | 0.8 | -0.6 |
| 17 | 0.8 | -0.7 |
| 18 | 0.8 | -0.8 |
| 19 | 0.8 | -0.9 |
| 20 | 0.9 | -0.5 |
| 21 | 0.9 | -0.6 |
| 22 | 0.9 | -0.7 |
| 23 | 0.9 | -0.8 |
| 24 | 0.9 | -0.9 |
#5 查看回测结果指标pa.evaluations_df
.dataframe tbody tr th:only-of-type { vertical-align: middle; } .dataframe tbody tr th { vertical-align: top; } .dataframe thead th { text-align: right; }
| buy | sell | __version | algorithm_return | algorithm_volatility | alpha | annual_algo_return | annual_bm_return | *g_position_days | *g_trade_return | benchmark_return | benchmark_volatility | beta | day_win_ratio | excess_return | information | lose_count | max_drawdown | max_drawdown_period | max_leverage | period_label | profit_loss_ratio | sharpe | sortino | trading_days | treasury_return | win_count | win_ratio | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | -0.5 | 101 | 2.88008 | 0.129651 | 0.103658 | 0.132149 | -0.0319802 | 66.1322 | 0.0157081 | -0.298868 | 0.275311 | 0.159895 | 0.515928 | 2.43077 | 0.627714 | 758 | 0.413689 | [2017-03-14, 2018-10-18] | 0 | 2019-03 | 1.95592 | 0.710741 | 0.894752 | 2731 | 0.449315 | 1220 | 0.616785 |
| 1 | 0.5 | -0.6 | 101 | 3.35066 | 0.132147 | 0.115787 | 0.144075 | -0.0319802 | 70.2541 | 0.0155423 | -0.298868 | 0.275311 | 0.162723 | 0.517393 | 2.90135 | 0.672222 | 752 | 0.402631 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.87874 | 0.787568 | 0.990435 | 2731 | 0.449315 | 1204 | 0.615542 |
| 2 | 0.5 | -0.7 | 101 | 4.77652 | 0.13747 | 0.14687 | 0.174152 | -0.0319802 | 78.2213 | 0.0160257 | -0.298868 | 0.275311 | 0.176699 | 0.521787 | 4.32721 | 0.791013 | 778 | 0.403218 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.06558 | 0.975857 | 1.22396 | 2731 | 0.449315 | 1180 | 0.602656 |
| 3 | 0.5 | -0.8 | 101 | 4.02125 | 0.156956 | 0.134292 | 0.159187 | -0.0319802 | 91.5854 | 0.0142144 | -0.298868 | 0.275311 | 0.209859 | 0.522885 | 3.57193 | 0.729779 | 802 | 0.4899 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.72246 | 0.759361 | 0.896422 | 2731 | 0.449315 | 1155 | 0.590189 |
| 4 | 0.5 | -0.9 | 101 | 4.20532 | 0.157668 | 0.138247 | 0.163013 | -0.0319802 | 93.4146 | 0.0142261 | -0.298868 | 0.275311 | 0.211635 | 0.523618 | 3.756 | 0.744634 | 803 | 0.479359 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.75981 | 0.780204 | 0.917871 | 2731 | 0.449315 | 1140 | 0.586722 |
| 5 | 0.6 | -0.5 | 101 | 2.92162 | 0.126971 | 0.104248 | 0.133253 | -0.0319802 | 61.0513 | 0.0208981 | -0.298868 | 0.275311 | 0.15275 | 0.513365 | 2.4723 | 0.630117 | 600 | 0.403831 | [2017-07-10, 2018-10-18] | 0 | 2019-03 | 2.13247 | 0.734439 | 0.915374 | 2731 | 0.449315 | 1086 | 0.644128 |
| 6 | 0.6 | -0.6 | 101 | 3.13411 | 0.130203 | 0.109909 | 0.13874 | -0.0319802 | 66.3814 | 0.0218798 | -0.298868 | 0.275311 | 0.155163 | 0.512999 | 2.6848 | 0.648851 | 597 | 0.420182 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.91137 | 0.758355 | 0.946028 | 2731 | 0.449315 | 1071 | 0.642086 |
| 7 | 0.6 | -0.7 | 101 | 4.37883 | 0.135553 | 0.138603 | 0.16651 | -0.0319802 | 73.7143 | 0.0224038 | -0.298868 | 0.275311 | 0.168017 | 0.517027 | 3.92951 | 0.75728 | 624 | 0.420065 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.06092 | 0.933282 | 1.165 | 2731 | 0.449315 | 1044 | 0.625899 |
| 8 | 0.6 | -0.8 | 101 | 3.4006 | 0.154525 | 0.119551 | 0.14527 | -0.0319802 | NaN | NaN | -0.298868 | 0.275311 | 0.198389 | NaN | 2.95128 | 0.671867 | NaN | 0.512813 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | NaN | 0.681252 | 0.803563 | 2731 | 0.449315 | NaN | NaN |
| 9 | 0.6 | -0.9 | 101 | 3.66359 | 0.15526 | 0.125766 | 0.151372 | -0.0319802 | 89.3025 | 0.0241132 | -0.298868 | 0.275311 | 0.199969 | 0.519956 | 3.21428 | 0.695055 | 622 | 0.502048 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.73581 | 0.717328 | 0.843774 | 2731 | 0.449315 | 1033 | 0.624169 |
| 10 | 0.7 | -0.5 | 101 | 3.26165 | 0.116597 | 0.111651 | 0.141912 | -0.0319802 | 57.5789 | 0.0235371 | -0.298868 | 0.275311 | 0.135308 | 0.516294 | 2.81233 | 0.662574 | 505 | 0.361376 | [2017-07-10, 2018-10-18] | 0 | 2019-03 | 2.63184 | 0.874054 | 1.15182 | 2731 | 0.449315 | 961 | 0.655525 |
| 11 | 0.7 | -0.6 | 101 | 3.59683 | 0.120096 | 0.119786 | 0.149853 | -0.0319802 | NaN | NaN | -0.298868 | 0.275311 | 0.137989 | NaN | 3.14751 | 0.690722 | NaN | 0.386532 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | NaN | 0.914716 | 1.2094 | 2731 | 0.449315 | NaN | NaN |
| 12 | 0.7 | -0.7 | 101 | 5.61576 | 0.12482 | 0.159632 | 0.188823 | -0.0319802 | 69.5086 | 0.0329793 | -0.298868 | 0.275311 | 0.150167 | 0.519956 | 5.16645 | 0.842955 | 493 | 0.390636 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.52431 | 1.1923 | 1.58202 | 2731 | 0.449315 | 955 | 0.65953 |
| 13 | 0.7 | -0.8 | 101 | 3.99844 | 0.146314 | 0.131664 | 0.158704 | -0.0319802 | 85.7179 | 0.0278659 | -0.298868 | 0.275311 | 0.180057 | 0.518491 | 3.54912 | 0.721186 | 527 | 0.500255 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.92501 | 0.811291 | 0.994318 | 2731 | 0.449315 | 923 | 0.636552 |
| 14 | 0.7 | -0.9 | 101 | 4.40002 | 0.147239 | 0.140007 | 0.166929 | -0.0319802 | 87.5983 | 0.0301974 | -0.298868 | 0.275311 | 0.181687 | 0.519224 | 3.9507 | 0.752165 | 526 | 0.490382 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.00192 | 0.862062 | 1.05387 | 2731 | 0.449315 | 912 | 0.634214 |
| 15 | 0.8 | -0.5 | 101 | 2.83365 | 0.114033 | 0.100171 | 0.130902 | -0.0319802 | 58.0833 | 0.0244777 | -0.298868 | 0.275311 | 0.128771 | 0.512999 | 2.38434 | 0.618829 | 457 | 0.323842 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | 2.61003 | 0.797149 | 1.04356 | 2731 | 0.449315 | 800 | 0.636436 |
| 16 | 0.8 | -0.6 | 101 | 3.22281 | 0.118192 | 0.110472 | 0.140955 | -0.0319802 | 63.8807 | 0.0266536 | -0.298868 | 0.275311 | 0.132222 | 0.512267 | 2.77349 | 0.654936 | 452 | 0.336422 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.2684 | 0.854158 | 1.12173 | 2731 | 0.449315 | 793 | 0.636948 |
| 17 | 0.8 | -0.7 | 101 | 4.17958 | 0.12107 | 0.132537 | 0.162486 | -0.0319802 | 69.0092 | 0.0292179 | -0.298868 | 0.275311 | 0.139634 | 0.515562 | 3.73026 | 0.738785 | 448 | 0.339207 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 2.40758 | 1.0117 | 1.32361 | 2731 | 0.449315 | 796 | 0.639871 |
| 18 | 0.8 | -0.8 | 101 | 3.05048 | 0.140188 | 0.10847 | 0.136612 | -0.0319802 | 82.4727 | 0.0244971 | -0.298868 | 0.275311 | 0.164753 | 0.515196 | 2.60116 | 0.635071 | 467 | 0.439964 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.79787 | 0.689158 | 0.837979 | 2731 | 0.449315 | 784 | 0.626699 |
| 19 | 0.8 | -0.9 | 101 | 3.33089 | 0.141119 | 0.115592 | 0.143598 | -0.0319802 | 84.9636 | 0.0248388 | -0.298868 | 0.275311 | 0.166631 | 0.515196 | 2.88158 | 0.661495 | 465 | 0.437352 | [2017-03-17, 2018-10-18] | 0 | 2019-03 | 1.92029 | 0.734118 | 0.889548 | 2731 | 0.449315 | 777 | 0.625604 |
| 20 | 0.9 | -0.5 | 101 | 3.00182 | 0.11246 | 0.104281 | 0.135355 | -0.0319802 | 55.4245 | 0.0285542 | -0.298868 | 0.275311 | 0.12401 | 0.512267 | 2.55251 | 0.634078 | 402 | 0.358847 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | 2.65347 | 0.847899 | 1.13081 | 2731 | 0.449315 | 713 | 0.639462 |
| 21 | 0.9 | -0.6 | 101 | 3.72464 | 0.115726 | 0.121846 | 0.152744 | -0.0319802 | 59.5888 | 0.0321571 | -0.298868 | 0.275311 | 0.126451 | 0.512999 | 3.27533 | 0.698092 | 396 | 0.348735 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | 2.50236 | 0.974234 | 1.30877 | 2731 | 0.449315 | 714 | 0.643243 |
| 22 | 0.9 | -0.7 | 101 | 4.82583 | 0.118881 | 0.1448 | 0.175065 | -0.0319802 | 64.8972 | 0.0357633 | -0.298868 | 0.275311 | 0.135241 | 0.518858 | 4.37651 | 0.785778 | 384 | 0.348215 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | 2.635 | 1.13614 | 1.51436 | 2731 | 0.449315 | 719 | 0.651859 |
| 23 | 0.9 | -0.8 | 101 | 3.54727 | 0.141443 | 0.120573 | 0.148713 | -0.0319802 | 80.3761 | 0.0277498 | -0.298868 | 0.275311 | 0.164771 | 0.518858 | 3.09796 | 0.67897 | 415 | 0.444037 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | 1.97284 | 0.768602 | 0.939948 | 2731 | 0.449315 | 692 | 0.625113 |
| 24 | 0.9 | -0.9 | 101 | 3.64107 | 0.142466 | 0.122887 | 0.150862 | -0.0319802 | NaN | NaN | -0.298868 | 0.275311 | 0.167063 | NaN | 3.19176 | 0.687321 | NaN | 0.440783 | [2017-07-07, 2018-10-18] | 0 | 2019-03 | NaN | 0.778163 | 0.946413 | 2731 | 0.449315 | NaN | NaN |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
