KNN算法简介
KNN 算法实际上是一句中国谚语智慧的体现:“物以类聚,人以群分”,是一种聚类分析的方法,也是目前最简单的无监督类学习方法。
我们在日常生活中有这样的推论,身边朋友都爱喝酒的人,可能是爱喝酒的人;身边朋友都认为身边朋友都爱喝酒的人可能是爱喝酒的人的人,可能是认为身边朋友都爱喝酒的人可能是爱喝酒的人的人。
基于这样的逻辑,如果现在我们有几个点,分布在二维平面上:
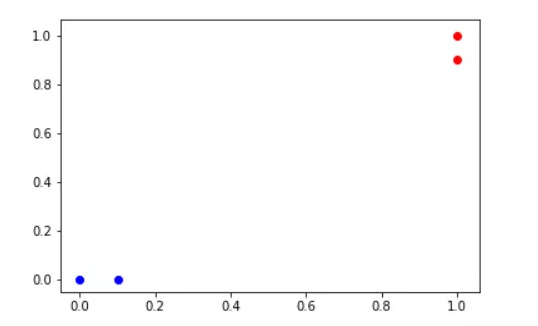
现在突然出现了一个这样颜色不明的点(这明明就是黑的)
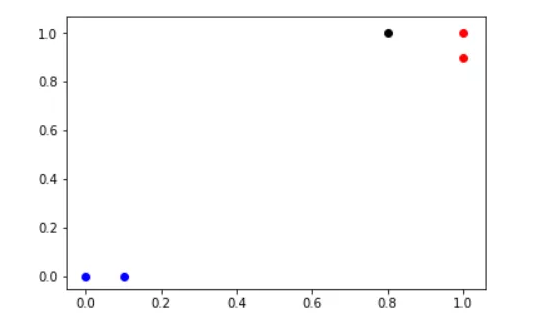
很自然的我们下意识的觉得这个点是蓝的!
好好好,别动手有话好商量,事实上正常人肯定觉得这个点颜色应该是红色的。
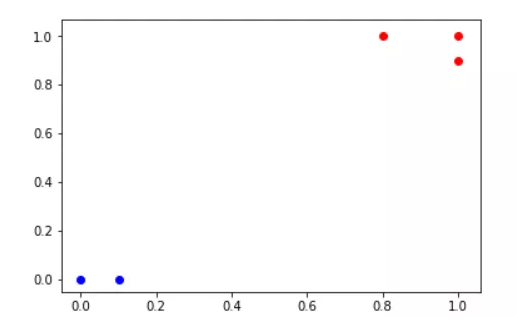
这种聚类思想可以运用到很多分类问题中,比如股票价格未来走势的预测(醒醒吧,也就这么顺口一说,要是准确率高我还会在这里写文章吗?)
这种方法的严谨的数学表达是:首先确定距离的度量方法,事实上在数学上有很多种距离的度量方法,比如切比雪夫距离,欧氏距离,曼哈顿距离,这些距离实际上对应的是一个叫做范数的数学概念,鉴于这篇文章不是数学讲堂,同时还指望着流量点击养家糊口,就不一一叙述了。这里我们给出对欧式距离(L2 范数)的计算方法
诶嘿,是不是突然发现很熟悉,然后读者们可能就要开始骂了,故弄什么玄虚,这不就是 n 维空间内点的直线距离吗,没有错,L2 范数对应的就是点在空间内部的直线距离。根据分类的标的不同,我们使用不同的距离度量方法来适应样本的独特性质,不过一般情况下使用直线距离就足够了,毕竟老夫也不是什么恶魔,况且 L2 范数已经具有相当良好的数学性质,比如连续,可导…跑题了,咳……
既然刚刚已经明确了距离的概念,这样当我们拥有一个非常完整的样本的情况下,特征完整标签明确。当我们想对一个新来的点或者一些样本进行分类的时候,我们可以逐一计算这个(些)新来的样本和已知的样本点之间的距离,然后取离这个点最近的 K 个已知样本。统计一下这些已知样本点对应标签的数量,选取出现次数最多的标签作为新来样本点的分类。
当然这个 K 参数是自行选择的,有一个小技巧是,K 参数尽量避免成为标签集合数量的倍数,原因试一试就知道了。
KNN 算法的优点在于:
①对病态数据不敏感(毕竟取了K个数据,有一两个病态的数据基本不影响结果。有的亲一定要杠一下,就要问了:要是全部样本都病了怎么办呢?亲,我们这边建议殴打给你样本数据的人)
②分类精度比较高
③对数据不需要预先的假设(比如强行规定他服从XX分布……金融分析最喜欢做的事ORZ)
KNN算法的缺点在于:
①计算复杂度高,大样本下计算时间长
②边缘样本分类精度明显下降
import talib
import pandas as pd
import numpy as np
import datetime
from jqdata import*
import matplotlib.pyplot as plt
#使用成交量,5日MA,5日波动率,预测三日后价格变化
#归一化函数
def turn_one(array):
range_num = array.max() - array.min()
min_num = array.min()
array = (array - min_num) / range_num
return array
#确定基准股票池,时间,获取价格
stock_list = get_index_stocks('000906.XSHG')
sample_price = get_price(stock_list,'2018-06-30','2018-11-30','1d',['close'])['close']
sample_price = sample_price.fillna(0)
#打标签,3日后涨为1,跌为-1,无变化为0
date_list = sample_price.index
trade_days = [i for i in get_all_trade_days()]
stock_col = sample_price.columns
deal_change = pd.DataFrame()
for date in date_list[4:len(date_list)-3]:
now_price = sample_price.loc[date,:]
future_date = trade_days[trade_days.index(date.date()) + 3]
future_price = sample_price.loc[future_date,:]
price_change = future_price - now_price
price_change[price_change > 0] = 1
price_change[price_change < 0] = -1
price_change[price_change == 0] = 0
deal_change[date] = price_change
deal_change = deal_change.T
#计算MA
MA_data = pd.DataFrame(index = date_list[4:len(date_list) - 3])
for i in sample_price.columns:
array_close = np.array(sample_price[i])
MA_data[i] = turn_one(talib.MA(array_close,timeperiod = 5)[4:len(array_close) - 3])
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:5: RuntimeWarning: invalid value encountered in true_divide """
#获取成交量
sample_vol = get_price(stock_list,'2018-06-30','2018-11-30','1d',['money'])['money']
VOL_df = pd.DataFrame(index = date_list[4:len(date_list) - 3])
for i in sample_vol.columns:
array_close = np.array(sample_vol[i])
VOL_df[i] = turn_one(array_close)[4:len(array_close) - 3]
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:5: RuntimeWarning: invalid value encountered in true_divide """
#获取五日波动率
STD_data = pd.DataFrame(index = date_list[4:len(date_list) - 3])
for i in sample_price.columns:
array_close = np.array(sample_price[i])
std_array = []
for j in range(4,len(array_close) - 3):
std_array.append(array_close[j-4:j].std())
std_array = turn_one(np.array(std_array))[:len(array_close) - 3]
STD_data[i] = std_array
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:5: RuntimeWarning: invalid value encountered in true_divide """
#每只股票时间序列储存在字典里
data_dict = {}
for stock in deal_change.columns:
data_dict[stock] = []
for date in deal_change.index:
current_data = []
current_data.append(MA_data.loc[date,stock])
current_data.append(STD_data.loc[date,stock])
current_data.append(VOL_df.loc[date,stock])
current_data.append(deal_change.loc[date,stock])
data_dict[stock].append(current_data)
data_dict[stock] = np.array(data_dict[stock])
#清洗数据,提取特征和标签
def DataCreat(data,test_part):
data_length = data.shape[0]
train_length = int((1 - test_part) * data_length)
test_length = data_length - train_length
train_Data = np.zeros((train_length,3))
test_Data = np.zeros((test_length,3))
train_label = []
test_label = []
index = 0
for array in data:
if index <= train_length - 1:
train_label.append(array[3])
train_Data[index] = array[:3]
else:
test_Data[index - train_length] = array[:3]
test_label.append(array[3])
index += 1
return train_Data,train_label,test_Data,test_label
#KNN L2范数计算方法
def deal_distance(train_data,test_vector,train_label,K):
KNN = ((train_data - test_vector)**2).sum(axis = 1).argsort()[:K+1]
predict_label = []
count_label = []
predict_set = set(train_label)
for index in KNN:
predict_label.append(train_label[index])
for label in predict_set:
count_label.append((predict_label.count(label)))
max_index = count_label.index(max(count_label))
return list(predict_set)[max_index]
#进行预测
def KNN_claassify_predict(data,K,part):
train_data,train_label,test_data,test_label = DataCreat(data,part)
preditc_results = []
for test_vector in test_data:
result = deal_distance(train_data,test_vector,train_label,K)
preditc_results.append(result)
return preditc_results
#不同参属下评估性能
def KNN_evaluat(data,K,part):
train_data,train_label,test_data,test_label = DataCreat(data,part)
predict = KNN_claassify_predict(data,K,part)
score = 0
for i in range(len(predict)):
if predict[i] == test_label[i]:
score += 1
else:
pass
right_rate = score/len(predict)
return right_rate
rate_list = []
for key in data_dict.keys():
params_list = [KNN_evaluat(data_dict[key],i,0.2) for i in range(3,20)]
mean_rate = sum(params_list)/len(params_list)
rate_list.append(mean_rate)
print('全市场股票涨跌预测准确率为:' + str(sum(rate_list)/len(rate_list)*100) + '%')
print('全市场股票涨跌预测最高准确率为:' + str(max(rate_list)*100) + '%')
全市场股票涨跌预测准确率为:53.45220588235294% 全市场股票涨跌预测最高准确率为:100.0%

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
