最近发现特质波动率因子选股效果不错,于是按照东方证券研报的思路做了一些研究。研究发现该因子确实有显著的选股能力,并且在CAPM、Fama-French三因子、Carhart四因子、Fama-French五因子这四个模型中,Fama-French三因子的特质波动率因子选股能力最好。该因子虽在多头部分表现略逊于流通市值因子,但在多空方面表现明显强于流通市值因子,也说明特质波动率因子具有很好的选股区分能力,并且在空头部分有良好的风险警示作用。
海外和国内股票市场都发行过很多低波动指数,该类指数通常用一段时间收益率的标准差来衡量股价的波动,长期来看表现优于对应的基准指数。股价的波动很大一部分是由市值、估值等一些公共的市场风险因子引起,剔除掉这些公共因素后的剩余波动称为个股的“特质波动”,由个股的自身特性决定。我们的研究发现A股市场也有“特质波动率之谜”现象,即低特质波动的股票,未来预期收益更高。
CAPM(Sharpe,1964)认为,当资本市场是完美的无摩擦市场时,公司的特质风险可以通过分散化投资抵消,因此特质风险与公司的预期收益率无关。
Levy(1978)理论上证明了投资者不能充分分散化投资时,特质风险对资产价格有影响。
Merton(1987)在不完全信息的基础上建立了一个一般均衡模型,该模型表示投资者所获得的信息是有限的,其构造的组合无法完全分散特质风险,投资者对这部分特质风险要求更高的回报,因此特质波动率与股票的预期收益率成正相关关系。
Ang、Hodirck、Xing & Zhang(2006)以美国的股票数据为样本,通过三因素模型残差项的标准差来度量股票特质波动率,发现股票特质波动率与横截面预期收益存在显著的负相关关系,而且这种现象不能由公司规模、账面市值比、动量、流动性、公司财务杠杆、交易量、换手率、价差、协偏度、分析师预测分歧程度等因素解释。
AHXZ(2009)将数据范围从美国市场扩展到23个发达国家,同样发现了这种负向关系。
特质波动率(Idiosyncratic Volatility, IV)与预期收益率的负向关系既不符合经典资产定价理论,也不符合基于不完全信息的定价理论,因此学术界称之为“特质波动率之谜”。
风险分解的逻辑如下:股票的收益率可以被一组公共因子和一个仅与该股票相关的特异因子解释,由公共因子的不确定性所导致的风险普遍存在于市场中的股票中,而由股票特质因子不确定性所导致的风险仅与个股相关。


股票的风险结构方程将股票的总体风险分为公共因子风险、因子协同风险以及特质风险。公共因子风险和因子协同风险是所有股票共有的风险,但不同股票由于对各个公共因子的暴露度不同会有所不同,公共因子风险对总风险的贡献一定为正,因子协同风险对总风险的贡献可正可负,当公共因子互不相关时因子协同风险为零。特质风险衡量的是股票自身所特有的风险,与公共因子波动带来的风险不相关,与其他股票的特质风险也不相关。然而特质风险不能被实际观察到,在实际应用中特质风险的度量依赖于公共因子的选择,不同的的公共因子组合会估计出不同的特质收益率,从而会有不同的特质风险度量。
构建股票风险结构方程的艺术在于公共因子的选择。遗漏掉重要的公共因子会忽视重要的风险维度,不利于对股票风险结构的把握,同时忽视的公共因子所带来的风险(因子自身的风险及与其他因子的协同风险)被错误的归为特质风险,从而使得特质风险的度量失真。纳入冗余的因子会给模型的估计带来困难、模型误差增大,冗余因子的存在对股票风险的归因也会造成不客观的结果。
参考研报选择,我们分别根据资本资产定价模型CAPM、Fama-French三因子模型、Carhart四因子模型、Fama-French五因子模型,从四个维度度量特质波动率,具体定义如下。
1.基于CAPM的特质波动率 IVCAPM

(T取243,代表1年内交易日天数)
2.基于Fama-French三因子模型的特质波动率 IVFF3

3.基于Carhart四因子模型的特质波动率 IVCARHART

4.基于Fama-French五因子模型的特质波动率 IVFF5
在Fama-French三因子模型的基础上加入盈利水平因子RMW和投资水平因子CMA,分别以ROE数据和总资产年增长率来度量,其选股及后续处理方式与之前模型里的SMB、HML因子保持一致。
因子有效性的检验一般基于两个维度:
1.计算因子值与接下来一段时间(一般为1个月)的累计收益率的相关系数,即信息系数IC,通过考察相关系数的大小和显著性等方面研究因子的有效性;
2.根据因子大小分组构建投资组合,通过分析不同组合的业绩表现来考察因子的有效性。
本文关于特质波动率有效性的检验也基于这两个维度。
IC检验
我们利用前1个月的日频数据分别拟合CAPM、Fama-French三因子、Carhart四因子、Fama-French五因子模型,四个模型残差的年化标准差即为四种特质波动率的观察值IVCAPM、IVFF3、IVCARHART、IVFF5。为了剔除计算相关系数过程中因子时间序列波动的影响,我们在计算相关系数之前先在横截面上对因子进行了Z-score标准化处理。标准化之后各期因子均有相同的均值和方差,剔除了因子时间序列上变化的影响。计算IC时选用的是spearman秩相关系数计算特质波动率因子值和个股收益率之间的相关性。利用2005年1月至2015年8月的所有样本点我们计算所得到的相关系数如下表所示。(表中流动市值对数和账面市值比BP作为业内常用的表现较好的对照因子。均值为样本期全部IC的均值;若某期IC相关性p值小于0.05,则称其为显著的,正\负显著比例即为显著的正\负IC占全样本的比例;IR为IC均值除以IC标准差,代表因子有效性的稳定性,其绝对值越大越稳定)
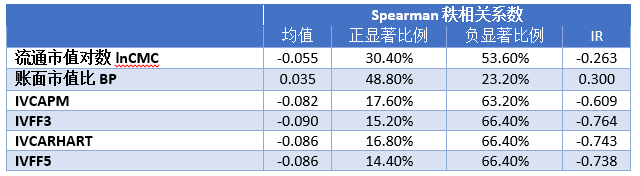
从因子IC指标角度来讲,横截面标准化后的特质波动率和股票未来的超额收益率有显著的负相关关系,IVFF3与超额收益的负相关程度最大,IC均值绝对值和IR绝对值也是最大。因此从IC角度来看,IVFF3为表现最好的特质波动率因子。
分组回测
我们基于多个特质波动率指标分组构建等权组合,考察各个组合的业绩表现。
结果显示:低的特质波动率意味着高的超额收益,IVFF3多空效益均明显优于其他方法。(蓝色柱代表第1组的超额收益、橙色柱为第10组的超额收益、绿色柱为两组超额收益差值,从左到右分别为流通市值,CAPM、FF3、CARHART、FF5)
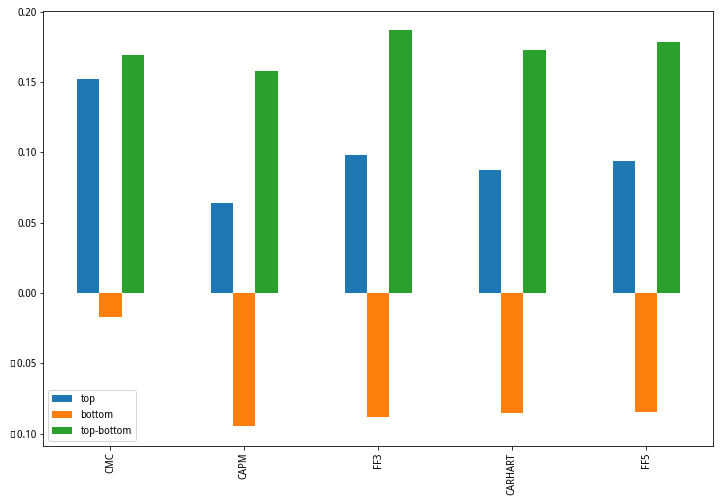
该因子虽在多头部分表现略逊于流通市值因子,但在多空方面表现明显强于流通市值因子,也说明特质波动率因子具有很好的选股区分能力,并且在空头部分有良好的风险警示作用。
下面简单展示一下表现较好的IVFF历史十分组表现,可以看出其具有优良的选股区分能力和单调性。
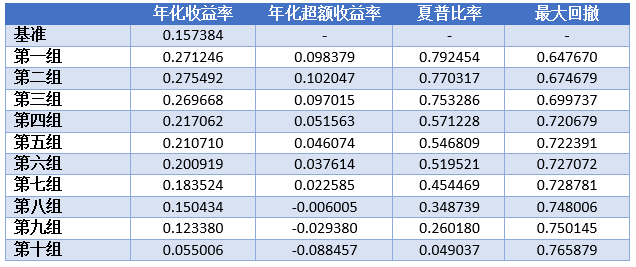
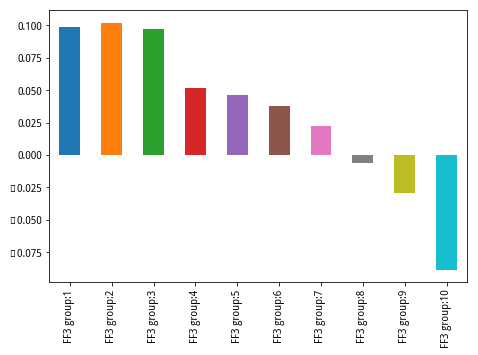
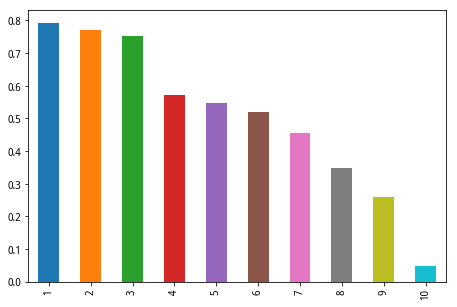
复现结果显示IVFF3具有优良的区分选股能力,IC和分组回测角度上IVFF3均明显优于其他方法,因此应选取IVFF3作为特质波动率因子的代表。
注:研究调用回测模块要换成自己的回测ID
#2019-03-13 修改代码细节问题,结论不受影响
#2019-03-21 修改CARHART四因子动量因子计算错误造成其效用偏高,修改结论为FF3效果在IC和分组回测两方面都是最好。精简代码。对于此错误带来的影响表示十分抱歉,感谢提供各方面修改建议的同学。
from jqdata import *
from jqlib.technical_analysis import *
from jqfactor import *
from scipy import stats
from statsmodels import regression
import datetime
import pandas as pd
import numpy as np
import statsmodels.api as sm
import warnings
warnings.filterwarnings('ignore')
#获取每月最后一个交易日(其余频次是获取第一个交易日,暂未改动)
def get_tradeday_list(start,end,frequency=None,count=None):
if count != None:
df = get_price('000001.XSHG',end_date=end,count=count)
else:
df = get_price('000001.XSHG',start_date=start,end_date=end)
if frequency == None or frequency =='day':
return df.index
else:
df['year-month'] = [str(i)[0:7] for i in df.index]
if frequency == 'month':
return df.drop_duplicates('year-month', keep = 'last').index
elif frequency == 'quarter':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='04') | (df['month']=='07') | (df['month']=='10') ]
return df.drop_duplicates('year-month').index
elif frequency =='halfyear':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='07')]
return df.drop_duplicates('year-month').index
#获取股票池
def get_stock(stockPool, begin_date):
if stockPool == 'HS300':
stockList = get_index_stocks('000300.XSHG', begin_date)
elif stockPool == 'ZZ500':
stockList = get_index_stocks('399905.XSHE', begin_date)
elif stockPool == 'ZZ800':
stockList = get_index_stocks('399906.XSHE', begin_date)
elif stockPool == 'A':
stockList = list(get_all_securities(['stock'], date = begin_date).index)
#剔除ST股
st_data = get_extras('is_st',stockList, count = 1,end_date = begin_date)
stockList = [stock for stock in stockList if not st_data[stock][0]]
#剔除*st股票
stockList = [stock for stock in stockList if '*' not in get_security_info(stock).display_name]
#剔除上市不足三个月的新股
stockList = delete_new(stockList, begin_date, n = 91)
#剔除停牌
suspended_info_df = get_price(stockList, end_date = begin_date, count = 1, frequency = 'daily', fields = 'paused')['paused']
stockList = [stock for stock in stockList if suspended_info_df[stock][0] == 0]
return stockList
#剔除新股
def delete_new(stocks, beginDate, n = 365):
stockList = []
for stock in stocks:
start_date = get_security_info(stock).start_date
if start_date < (beginDate - datetime.timedelta(days = n)):
stockList.append(stock)
return stockList
def get_factor_data1(stock, date):
q = query(valuation.circulating_market_cap, valuation.code).filter(valuation.code.in_(stock))
df = get_fundamentals(q, date)
df[factor] = df[factor] * 1e8
df[factor] = df[factor].apply(np.log)
df.index = df['code'].tolist()
del df['code']
return df
def get_factor_data2(stocks, start_date, end_date):
if factor == 'CAPM':
factor_data = hetero_factor(stocks, start_date, end_date)
elif factor == 'FF3':
factor_data = FF3(stocks, start_date, end_date)
elif factor == 'CARHART':
factor_data = CARHART(stocks, start_date, end_date)
elif factor == 'FF5':
factor_data = FF5(stocks, start_date, end_date)
elif factor == 'BP':
q = query(valuation.code, (balance.total_owner_equities/valuation.circulating_market_cap/1e8).label("BP")).filter(valuation.code.in_(stocks))
factor_data = get_fundamentals(q, end_date)
factor_data.index = factor_data['code'].tolist()
del factor_data['code']
return factor_data
#自定义因子库
global custom_factors
custom_factors = ['CAPM', 'FF3', 'CARHART', 'FF5', 'BP']
#计算CAPM特质波动率
def hetero_factor(stocks, start_date, end_date, rf = 0.04):
#设置统计范围
quote = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
ret = quote.pct_change()
ret.dropna(how ='all', inplace = True)
ret.fillna(0, inplace = True)
#构造市场基准收益:流通市值加权
q = query(valuation.circulating_market_cap, valuation.code).filter(valuation.code.in_(stocks))
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#df = (df * 1e8).apply(np.log)
df = df/df.sum()
ret_b = pd.DataFrame(np.dot(ret, df), index = ret.index)
#OLS计算hetero
hetero = {}
for stock in ret.columns:
hetero[stock] = {'vol': linreg(ret_b - rf/252, ret[stock] - rf/252)}
#规范格式
hetero = pd.DataFrame(hetero).T
hetero.dropna(inplace = True)
hetero.columns = ['score']
#返回特质波动率vol
return hetero
#求Fama-French三因子模型特质波动率
def FF3(stocks, start_date, end_date, rf = 0.04):
LoS=len(stocks)
#查询三因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
#indicator.roe,
#balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['sw_l1', 'market_cap'], date = start_date, axis = 0)
n = int(LoS/3)
#选出特征股票组合
S=df.sort_values('circulating_market_cap').index.tolist()[: n]
B=df.sort_values('circulating_market_cap').index.tolist()[LoS - n:]
L=df.sort_values('BP').index.tolist()[: n]
H=df.sort_values('BP').index.tolist()[LoS - n:]
#df5 = (df['circulating_market_cap'] * 1e8).apply(np.log)
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
#用股票池,流通市值为权重作为市场基准
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
#将因子们计算好并且放好
X = pd.DataFrame({"RM":RM, "SMB":SMB, "HML":HML})
# 对样本数据进行线性回归并计算残差
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是残差
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
#求Carhart四因子模型特质波动率
def CARHART(stocks, start_date, end_date, rf = 0.04):
LoS=len(stocks)
#查询四因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
#indicator.roe,
#balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['sw_l1', 'market_cap'], date = end, axis = 0)
n = int(LoS/3)
#选出特征股票组合
S=df.sort_values('circulating_market_cap').index.tolist()[:n]
B=df.sort_values('circulating_market_cap').index.tolist()[LoS - n:]
L=df.sort_values('BP').index.tolist()[:n]
H=df.sort_values('BP').index.tolist()[LoS - n:]
#df5 = (df['circulating_market_cap'] * 1e8).apply(np.log)
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#动量(反转)因子
prior_date = list(get_tradeday_list(start = None, end = start_date, frequency = 'month', count = 24).date)[0]
df22 = get_price(stocks, start_date = prior_date, end_date = start_date, fields=['close'])['close']
df42 = pd.DataFrame(df22.iloc[-1, :] / df22.iloc[0, :] - 1, columns = ['ret'])
df42.replace(0, np.nan)
df42.fillna(0, inplace = True)
LO = df42.sort_values('ret').index.tolist()[: n]
W = df42.sort_values('ret').index.tolist()[LoS - n:]
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
#价格数据股票比财务数据多
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
MOM = list(np.dot(df4[LO], df6.loc[LO] / df6.loc[LO].sum()) - np.dot(df4[W], df6.loc[W] / df6.loc[W].sum()))
#用股票池,流通市值为权重作为市场基准
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
#将因子们计算好并且放好
X=pd.DataFrame({"RM": RM, "SMB": SMB, "HML": HML, "MOM": MOM})
# 对样本数据进行线性回归并计算残差
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是残差
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
#求Fama-French五因子模型特质波动率
def FF5(stocks, start_date, end_date, rf = 0.04):
LoS=len(stocks)
#查询五因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
indicator.roe,
balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['market_cap'], date = start_date, axis = 0)
n = int(LoS/3)
#计算5因子再投资率的时候需要跟一年前的数据比较,所以单独取出计算
ldf = get_fundamentals(q, end_date - datetime.timedelta(365))
# 若前一年的数据不存在,则暂且认为Inv=0
if len(ldf) == 0:
ldf = df
df["Inv"] = np.log(df["Inv"] / ldf["Inv"])
#选出特征股票组合
S=df.sort_values('circulating_market_cap').index.tolist()[:n]
B=df.sort_values('circulating_market_cap').index.tolist()[LoS-n:]
L=df.sort_values('BP').index.tolist()[:n]
H=df.sort_values('BP').index.tolist()[LoS-n:]
W=df.sort_values('roe').index.tolist()[:n]
R=df.sort_values('roe').index.tolist()[LoS-n:]
C=df.sort_values('Inv').index.tolist()[:n]
A=df.sort_values('Inv').index.tolist()[LoS-n:]
#df5 = (df['circulating_market_cap'] * 1e8).apply(np.log)
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
RMW = list(np.dot(df4[R], df5.loc[R] / df5.loc[R].sum()) - np.dot(df4[W], df5.loc[W] / df5.loc[W].sum()))
CMA = list(np.dot(df4[C], df5.loc[C] / df5.loc[C].sum()) - np.dot(df4[A], df5.loc[A] / df5.loc[A].sum()))
#用股票池,流通市值为权重作为市场基准
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
RMW.drop(RMW.index[0], inplace = True)
CMA.drop(CMA.index[0], inplace = True)
#将因子们计算好并且放好
X=pd.DataFrame({"RM":RM, "SMB":SMB, "HML":HML, "RMW":RMW, "CMA" : CMA})
# 对样本数据进行线性回归并计算残差
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是残差
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
#9
# 辅助线性回归的函数
# 输入:X:回归自变量 Y:回归因变量 完美支持list,array,DataFrame等三种数据类型
# 输出:参数估计结果-list类型
def linreg(X,Y):
X=sm.add_constant(array(X, dtype=float))
Y=array(Y)
results = sm.OLS(Y, X).fit()
return results.resid.std() * sqrt(252)
#因子值数据处理,最后一个参数决定是否做市值行业中性化,默认做
def data_preprocessing(factor_data, stockList, industry_code, date, ind_neutral = True):
#去极值,参数来自光大研报
factor_data = winsorize_med(factor_data, scale = 3, inf2nan = False, axis = 0)
#缺失值处理
nan_ratio = 1 - factor_data.count() / len(factor_data)
if nan_ratio[0] > 0.2:
print(str(date) + '数据缺失率为:' + str(nan_ratio))
factor_data = replace_nan_indu(factor_data, stockList, industry_code, date)
#标准化处理
factor_data = standardlize(factor_data, axis = 0)
#中性化处理
if ind_neutral == True:
factor_data = neutralize(factor_data, how = ['sw_l1', 'market_cap'], date = date, axis = 0)
return factor_data
#缺失值处理
def replace_nan_indu(factor_data, stockList, industry_code, date):
#把nan用行业中位数代替,依然会有nan,此时用所有股票中位数代替
i_Constituent_Stocks = {}
data_temp = pd.DataFrame(index = industry_code, columns = factor_data.columns)
for i in industry_code:
temp = get_industry_stocks(i, date)
i_Constituent_Stocks[i] = list(set(temp).intersection(set(stockList)))
data_temp.loc[i] = nanmedian(array(factor_data.loc[i_Constituent_Stocks[i], :]))
for factor in data_temp.columns:
#行业缺失值用所有行业中位数代替
null_industry = list(data_temp.loc[pd.isnull(data_temp[factor]), factor].keys())
for i in null_industry:
data_temp.loc[i, factor] = nanmedian(array(data_temp[factor]))
#查询空值所在位置并填充
null_stock = list(factor_data.loc[pd.isnull(factor_data[factor]), factor].keys())
for i in null_stock:
industry = get_industry_name(i_Constituent_Stocks, i)
if industry:
factor_data.loc[i, factor] = data_temp.loc[industry[0], factor]
else:
factor_data.loc[i, factor] = nanmedian(array(factor_data[factor]))
return factor_data
#取股票对应行业
def get_industry_name(i_Constituent_Stocks, value):
return [k for k, v in i_Constituent_Stocks.items() if value in v]
#获取所需数据并存储
def get_df(period):
#申万更新以前
industry_old_code=['801010','801020','801030','801040','801050','801080','801110','801120','801130','801140','801150',\
'801160','801170','801180','801200','801210','801230']
#申万更新以后
industry_new_code = ['801010','801020','801030','801040','801050','801080','801110','801120','801130','801140','801150',\
'801160','801170','801180','801200','801210','801230','801710','801720','801730','801740','801750',\
'801760','801770','801780','801790','801880','801890']
#时段内全部因子值及当期收益率
df = pd.DataFrame(index = get_stock(universe, period[-1]))
for i in range(1, len(period) - 1):
if period[i] < datetime.datetime.date(datetime.datetime.strptime('2014-02-21', '%Y-%m-%d')):
industry_code = industry_old_code
else:
industry_code = industry_new_code
all_stock = get_stock(universe, period[i])
#获取数据
if factor == 'circulating_market_cap': #可以从get_fundamentals直接取到因子值的因子
data = get_factor_data1(all_stock, period[i])
elif factor in custom_factors: #自定义库取到的因子
data = get_factor_data2(all_stock, period[i - 1], period[i])
#处理数据
p_data = data_preprocessing(data, all_stock, industry_code, period[i], ind_neutral = False)
p_data.columns = [str(period[i]) + factor]
df = pd.concat([df, p_data], axis = 1)
price = get_price(p_data.index.tolist(), start_date = period[i], end_date = period[i + 1], fields = ['close'])['close']
#无法相对于中证全指的超额收益,因为2005年还没有
ret = pd.DataFrame((price.iloc[-1, :] / price.iloc[0, :]) - 1, columns = [str(period[i]) + '收益率'])
ret.fillna(nanmedian(ret), inplace = True)
df = pd.concat([df, ret], axis = 1)
df.dropna(how = 'all', inplace = True)
return df
#计算IC
def get_IC(df):
#IC值序列
IC = []
S = []
for i in range(1, len(period) - 1):
raw = pd.DataFrame(index = df.index)
raw['0'] = df[str(period[i]) + factor]
raw['1'] = df[str(period[i]) + '收益率']
raw.dropna(inplace = True)
ic, p = stats.spearmanr(raw, axis = 0, nan_policy = 'omit')
IC.append(ic)
#显著性检验
if p < 0.05:
if ic > 0:
S.append('pos')
elif ic < 0:
S.append('neg')
else:
S.append('non')
else:
S.append('non')
return IC, S
#汇总结果
def draw_conclusion(period):
df = get_df(period)
#f, t_f = get_f_t(df)
IC, S = get_IC(df)
conclusion = pd.DataFrame(index = [factor])
conclusion['IC均值'] = nanmean(IC)
conclusion['IC正显著比例'] = S.count('pos') / len(S)
conclusion['IC负显著比例'] = S.count('neg') / len(S)
conclusion['abs(IC)>0.02比例'] = len([i for i in IC if abs(i) > 0.02]) / len(IC)
conclusion['IR'] = nanmean(IC) / std(IC)
print(conclusion.T)
return None
#控制获取数据时段(因为数据库只到2005年1月1日,且IC计算要前一个月的数据,因此从1月底开始计算)
start_date = '2005-01-31'
end_date = '2015-08-01'
period = get_tradeday_list(start = start_date, end = end_date, frequency = 'month').date
#所需股票池,可选'HS300','ZZ500','ZZ800','A'
global universe
universe = 'A'
#所需因子
global factor
factors = ['CAPM', 'FF3', 'CARHART', 'FF5', 'circulating_market_cap', 'BP']
#得到IC检验结果(时间较长)
for f in factors:
factor = f
draw_conclusion(period)
分组回测用自己的代码,数据处理使回测与研究模块保持一致
#回测用代码
code = '''
# 导入函数库
from jqdata import *
from jqfactor import *
import datetime as dt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels import regression
# 初始化函数,设定基准等等
def initialize(context):
# 设定中证全指作为基准
set_benchmark({'000002.XSHG': 0.5, '399107.XSHE': 0.5})
# 开启动态复权模式(真实价格)
set_option('use_real_price', True)
log.set_level('order', 'error')
#第几组
g.group = 1
g.method = 'FF5'
## 运行函数(reference_security为运行时间的参考标的;传入的标的只做种类区分,因此传入'000300.XSHG'或'510300.XSHG'是一样的)
# 开盘前运行
run_monthly(before_market_open, monthday = -1, time='before_open', reference_security = '399107.XSHE')
# 开盘时运行
run_monthly(market_open, monthday = -1, time='open', reference_security = '399107.XSHE')
## 开盘前运行函数
def before_market_open(context):
#设置排序方式
if g.method == 'BP':
g.asc = False
else:
g.asc = True
#设置滑点、手续费
set_slip_fee(context)
#取全A作为股票池
all_stocks = list(get_all_securities(['stock'], date = context.current_dt).index)
feasible_stocks = set_feasible_stocks(context, all_stocks)
if g.method == 'CAPM':
factor = hetero_factor(feasible_stocks, context.current_dt)
elif g.method == 'FF3':
factor = FF3(feasible_stocks, context.current_dt)
elif g.method == 'CARHART':
factor = CARHART(feasible_stocks, context.current_dt)
elif g.method == 'FF5':
factor = FF5(feasible_stocks, context.current_dt)
elif g.method == 'circulating_market_cap':
q = query(valuation.circulating_market_cap, valuation.code).filter(valuation.code.in_(feasible_stocks))
factor = get_fundamentals(q, context.current_dt)
factor.index = factor['code'].tolist()
del factor['code']
factor.columns = ['score']
elif g.method == 'BP':
q = query(1.0 / valuation.pb_ratio, valuation.code).filter(valuation.code.in_(feasible_stocks))
factor = get_fundamentals(q, context.current_dt)
factor.index = factor['code'].tolist()
del factor['code']
factor.columns = ['score']
factor = factor.loc[factor['score'] > 0]
#排序
factor = factor.sort('score', ascending = g.asc)
n = int(len(factor)/10)
#分组取样
if g.group == 10:
g.tobuy_list = factor.index[(g.group - 1) * n :]
else:
g.tobuy_list = factor.index[(g.group - 1) * n : g.group * n]
#1
#设置可行股票池,剔除st、停牌股票,输入日期
def set_feasible_stocks(context, stockList):
#剔除ST股
st_data = get_extras('is_st', stockList, count = 1, end_date = context.current_dt)
stockList = [stock for stock in stockList if not st_data[stock][0]]
#剔除*st股票
stockList = [stock for stock in stockList if '*' not in get_security_info(stock).display_name]
#剔除上市不足3月的新股
stockList = delete_new(stockList, context.current_dt, n = 91)
#剔除停牌
suspended_info_df = get_price(stockList, end_date = context.current_dt, count = 1, frequency = 'daily', fields = 'paused')['paused']
stockList = [stock for stock in stockList if suspended_info_df[stock][0] == 0]
return stockList
#剔除新股
def delete_new(stocks, beginDate, n = 365):
stockList = []
for stock in stocks:
start_date = get_security_info(stock).start_date
if start_date < dt.datetime.date(beginDate - dt.timedelta(days = n)):
stockList.append(stock)
return stockList
# 根据不同的时间段设置滑点与手续费
def set_slip_fee(context):
# 将滑点设置为0
set_slippage(FixedSlippage(0))
# 根据不同的时间段设置手续费
dt=context.current_dt
if dt>datetime.datetime(2013,1, 1):
set_commission(PerTrade(buy_cost=0.0003,
sell_cost=0.0013,
min_cost=5))
elif dt>datetime.datetime(2011,1, 1):
set_commission(PerTrade(buy_cost=0.001,
sell_cost=0.002,
min_cost=5))
elif dt>datetime.datetime(2009,1, 1):
set_commission(PerTrade(buy_cost=0.002,
sell_cost=0.003,
min_cost=5))
else:
set_commission(PerTrade(buy_cost=0.003,
sell_cost=0.004,
min_cost=5))
## 开盘时运行函数
def market_open(context):
#调仓,先卖出股票
for stock in context.portfolio.long_positions:
if stock not in g.tobuy_list:
order_target_value(stock, 0)
#再买入新股票
total_value = context.portfolio.total_value # 获取总资产
for i in range(len(g.tobuy_list)):
value = total_value / len(g.tobuy_list) # 确定每个标的的权重
order_target_value(g.tobuy_list[i], value) # 调整标的至目标权重
#查看本期持仓股数
print(len(context.portfolio.long_positions))
#计算CAPM特质波动率
def hetero_factor(stocks, end_date, rf = 0.04):
#设置统计范围
start_date = list(get_tradeday_list(start = None, end = end_date, frequency = 'month', count = 24).date)[0]
quote = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
ret = quote.pct_change()
ret.dropna(how ='all', inplace = True)
#构造市场基准收益:流通市值加权
q = query(valuation.circulating_market_cap, valuation.code).filter(valuation.code.in_(stocks))
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
df = df/df.sum()
ret_b = pd.DataFrame(np.dot(ret, df), index = ret.index)
#OLS计算hetero_
hetero = {}
for stock in ret.columns:
hetero[stock] = {'vol': linreg(ret_b - rf/252, ret[stock] - rf/252)}
#规范格式
hetero = pd.DataFrame(hetero).T
hetero.dropna(inplace = True)
hetero.columns = ['score']
#返回特质波动率vol
return hetero
#求Fama-French三因子模型特质波动率
def FF3(stocks, end_date, rf = 0.04):
LoS=len(stocks)
#查询三因子/五因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
#indicator.roe,
#balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
start_date = list(get_tradeday_list(start = None, end = end_date, frequency = 'month', count = 24).date)[0]
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['sw_l1', 'market_cap'], date = start_date, axis = 0)
#选出特征股票组合
S=df.sort('circulating_market_cap').index.tolist()[:LoS/3]
B=df.sort('circulating_market_cap').index.tolist()[LoS-LoS/3:]
L=df.sort('BP').index.tolist()[:LoS/3]
H=df.sort('BP').index.tolist()[LoS-LoS/3:]
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
#用股票池,流通市值为权重作为市场基准
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
#将因子们计算好并且放好
X=pd.DataFrame({"RM":RM, "SMB":SMB, "HML":HML})
# 对样本数据进行线性回归并计算残差标准差
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是残差标准差
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
#9
# 辅助线性回归的函数
# 输入:X:回归自变量 Y:回归因变量 完美支持list,array,DataFrame等三种数据类型
# 输出:参数估计结果-list类型
def linreg(X,Y):
X=sm.add_constant(array(X))
Y=array(Y)
results = sm.OLS(Y, X).fit()
return results.resid.std() * sqrt(252)
#求Carhart四因子模型特质波动率
def CARHART(stocks, end_date, rf = 0.04):
LoS=len(stocks)
#查询三因子/五因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
#indicator.roe,
#balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
start_date = list(get_tradeday_list(start = None, end = end_date, frequency = 'month', count = 24).date)[0]
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['sw_l1', 'market_cap'], date = start_date, axis = 0)
#选出特征股票组合
S=df.sort('circulating_market_cap').index.tolist()[:LoS/3]
B=df.sort('circulating_market_cap').index.tolist()[LoS-LoS/3:]
L=df.sort('BP').index.tolist()[:LoS/3]
H=df.sort('BP').index.tolist()[LoS-LoS/3:]
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#动量(反转)因子
prior_date = list(get_tradeday_list(start = None, end = start_date, frequency = 'month', count = 24).date)[0]
df22 = get_price(stocks, start_date = prior_date, end_date = start_date, fields=['close'])['close']
df42 = pd.DataFrame(df22.iloc[-1, :] / df22.iloc[0, :] - 1, columns = ['ret'])
df42.replace(0, np.nan)
df42.fillna(0, inplace = True)
LO = df42.sort('ret').index.tolist()[:LoS/3]
W = df42.sort('ret').index.tolist()[LoS-LoS/3:]
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
#价格数据股票比财务数据多
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
MOM = list(np.dot(df4[LO], df6.loc[LO] / df6.loc[LO].sum()) - np.dot(df4[W], df6.loc[W] / df6.loc[W].sum()))
#用股票池,流通市值为权重作为市场基准
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
#将因子们计算好并且放好
X=pd.DataFrame({"RM": RM, "SMB": SMB, "HML": HML, "MOM": MOM})
# 对样本数据进行线性回归并计算ai
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是alpha
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
#求Fama-French五因子模型特质波动率
def FF5(stocks, end_date, rf = 0.04):
LoS=len(stocks)
#查询三因子/五因子的语句
q = query(
valuation.code,
valuation.circulating_market_cap,
(balance.total_owner_equities/valuation.circulating_market_cap/100000000.0).label("BP"),
indicator.roe,
balance.total_assets.label("Inv")
).filter(
valuation.code.in_(stocks)
)
start_date = list(get_tradeday_list(start = None, end = end_date, frequency = 'month', count = 24).date)[0]
df = get_fundamentals(q, start_date)
df.index = df['code']
del df['code']
#中性化
#df = neutralize(df, how = ['market_cap'], date = end_date, axis = 0)
#计算5因子再投资率的时候需要跟一年前的数据比较,所以单独取出计算
ldf = get_fundamentals(q, start_date - datetime.timedelta(365))
# 若前一年的数据不存在,则暂且认为Inv=0
if len(ldf) == 0:
ldf = df
df["Inv"] = np.log(df["Inv"] / ldf["Inv"])
#选出特征股票组合
S=df.sort('circulating_market_cap').index.tolist()[:LoS/3]
B=df.sort('circulating_market_cap').index.tolist()[LoS-LoS/3:]
L=df.sort('BP').index.tolist()[:LoS/3]
H=df.sort('BP').index.tolist()[LoS-LoS/3:]
W=df.sort('roe').index.tolist()[:LoS/3]
R=df.sort('roe').index.tolist()[LoS-LoS/3:]
C=df.sort('Inv').index.tolist()[:LoS/3]
A=df.sort('Inv').index.tolist()[LoS-LoS/3:]
df5 = df['circulating_market_cap']
# 获得样本期间的股票价格并计算日收益率
df2 = get_price(stocks, start_date = start_date, end_date = end_date, fields=['close'])['close']
df4 = df2.pct_change()
df4.dropna(how ='all', inplace = True)
df4.fillna(0, inplace = True)
#求因子的值,按流通市值加权
SMB = list(np.dot(df4[S], df5.loc[S] / df5.loc[S].sum()) - np.dot(df4[B], df5.loc[B] / df5.loc[B].sum()))
HML = list(np.dot(df4[H], df5.loc[H] / df5.loc[H].sum()) - np.dot(df4[L], df5.loc[L] / df5.loc[L].sum()))
RMW = list(np.dot(df4[R], df5.loc[R] / df5.loc[R].sum()) - np.dot(df4[W], df5.loc[W] / df5.loc[W].sum()))
CMA = list(np.dot(df4[C], df5.loc[C] / df5.loc[C].sum()) - np.dot(df4[A], df5.loc[A] / df5.loc[A].sum()))
#用股票池,流通市值为权重作为市场基准
df6 = df5.loc[df4.columns]
df6.fillna(df5.mean(), inplace = True)
RM = list(np.dot(df4, df6 / df6.sum()) - rf/252)
if len(SMB) > len(RM):
SMB.drop(SMB.index[0], inplace = True)
HML.drop(HML.index[0], inplace = True)
RMW.drop(RMW.index[0], inplace = True)
CMA.drop(CMA.index[0], inplace = True)
#将因子们计算好并且放好
X=pd.DataFrame({"RM":RM, "SMB":SMB, "HML":HML, "RMW":RMW, "CMA" : CMA})
# 对样本数据进行线性回归并计算ai
t_scores=[0.0] * LoS
for i in range(LoS):
t_stock = stocks[i]
t_r = linreg(X, df4[t_stock] - rf/252)
t_scores[i] = t_r
#这个scores就是alpha
scores = pd.DataFrame({'score': t_scores}, index = stocks)
return scores
def get_tradeday_list(start,end,frequency=None,count=None):
if count != None:
df = get_price('000001.XSHG',end_date=end,count=count)
else:
df = get_price('000001.XSHG',start_date=start,end_date=end)
if frequency == None or frequency =='day':
return df.index
else:
df['year-month'] = [str(i)[0:7] for i in df.index]
if frequency == 'month':
return df.drop_duplicates('year-month', take_last = True).index
elif frequency == 'quarter':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='04') | (df['month']=='07') | (df['month']=='10') ]
return df.drop_duplicates('year-month').index
elif frequency =='halfyear':
df['month'] = [str(i)[5:7] for i in df.index]
df = df[(df['month']=='01') | (df['month']=='07')]
return df.drop_duplicates('year-month').index
## 收盘后运行函数
def after_market_close(context):
pass
'''
#研究调用回测
created_bt_ids = []
methods = ['circulating_market_cap', 'CAPM', 'FF3', 'CARHART', 'FF5']
for method in methods:
#取第一组和第十组进行回测
for i in [1, 10]:
algorithm_id = "5231f150a4b39e3799b1dbf12ce721d5" #用自己的策略ID
extra_vars = {'group': i, 'method': method}
params = {
"algorithm_id": algorithm_id,
"start_date": "2005-02-27",
"end_date": "2015-08-01",
"frequency": "day",
"initial_cash": "30000000",
"initial_positions": None,
"extras": extra_vars,
"name" : method + ' group:' + str(i)
}
created_bt_ids.append(create_backtest(code = code, **params))
#等上个模块的回测全部运行结束再运行这个模块
#先获取基准收益和交易日信息
gt = get_backtest(backtest_id = created_bt_ids[0])
res = gt.get_results()
b_return = []
t = []
for r in res:
b_return.append(r['benchmark_returns'])
t.append(r['time'])
#建立df存储数据
data = pd.DataFrame(index = t)
data['b_return'] = b_return
#填入不同参数下的收益数据
for i in range(len(created_bt_ids)):
gt = get_backtest(backtest_id = created_bt_ids[i])
res = gt.get_results()
name = gt.get_params()['name']
s_return = []
for r in res:
s_return.append(r['returns'])
data[name] = s_return
#作五个因子多空效果简易图
dat = (data.iloc[-1, :] + 1)
new_dat = ((dat / dat[0]) ** (1/10.5) - 1).drop('b_return')
df_agg = pd.DataFrame(index = ['top', 'bottom', 'top-bottom'], columns = ['CMC', 'CAPM', 'FF3', 'CARHART', 'FF5'])
for i in range(len(df_agg.columns)):
df_agg[df_agg.columns[i]] = [new_dat[2*i], new_dat[2*i + 1], new_dat[2*i] - new_dat[2*i + 1]]
df_agg.T.plot.bar(figsize = (12,8))
#研究调用回测
created_bt_ids = []
method = 'FF3'
#取全部组别进行回测
for i in range(1, 11):
algorithm_id = "5231f150a4b39e3799b1dbf12ce721d5" #用自己的策略ID
extra_vars = {'group': i, 'method': method}
params = {
"algorithm_id": algorithm_id,
"start_date": "2005-02-27",
"end_date": "2015-08-01",
"frequency": "day",
"initial_cash": "30000000",
"initial_positions": None,
"extras": extra_vars,
"name" : method + ' group:' + str(i)
}
created_bt_ids.append(create_backtest(code = code, **params))
#等上个模块的回测全部运行结束再运行这个模块
#先获取基准收益和交易日信息
gt = get_backtest(backtest_id = created_bt_ids[0])
res = gt.get_results()
b_return = []
t = []
for r in res:
b_return.append(r['benchmark_returns'])
t.append(r['time'])
#建立df存储数据
data = pd.DataFrame(index = t)
data['b_return'] = b_return
#填入不同参数下的收益数据
for i in range(len(created_bt_ids)):
gt = get_backtest(backtest_id = created_bt_ids[i])
res = gt.get_results()
name = gt.get_params()['name']
s_return = []
for r in res:
s_return.append(r['returns'])
data[name] = s_return
#年化超额收益图
dat = (data.iloc[-1, :] + 1)
((dat / dat[0]) ** (1/10.5) - 1).drop('b_return').plot.bar(figsize = (7.5, 5))
#夏普比率图
sharpe = []
max_drawdown = []
name = range(1, 11)
for i in range(len(created_bt_ids)):
gt = get_backtest(backtest_id = created_bt_ids[i])
sharpe.append(gt.get_risk()['sharpe'])
max_drawdown.append(gt.get_risk()['max_drawdown'])
sharpe = pd.Series(sharpe, index = name)
max_drawdown = pd.Series(max_drawdown, index = name)
sharpe.plot.bar(figsize = (7.5, 5))

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
