@911-JoinQuant聚宽  求精华
1.股市中由于股价的波动性，使得我们很难能够顺利的预测股价涨跌。
2.但是有一门学科正好有种工具就是用于数据波动性的平滑处理-信号处理
3.信号处理中，我们常常使用滤波器来平滑处理数据波动（过滤数据波动）
4.我在网上找到一个简单的滤波函数将其翻译成Python语言（原为c语言），做了研究策略的测试，发现真实可用。现在将思路分享给大家

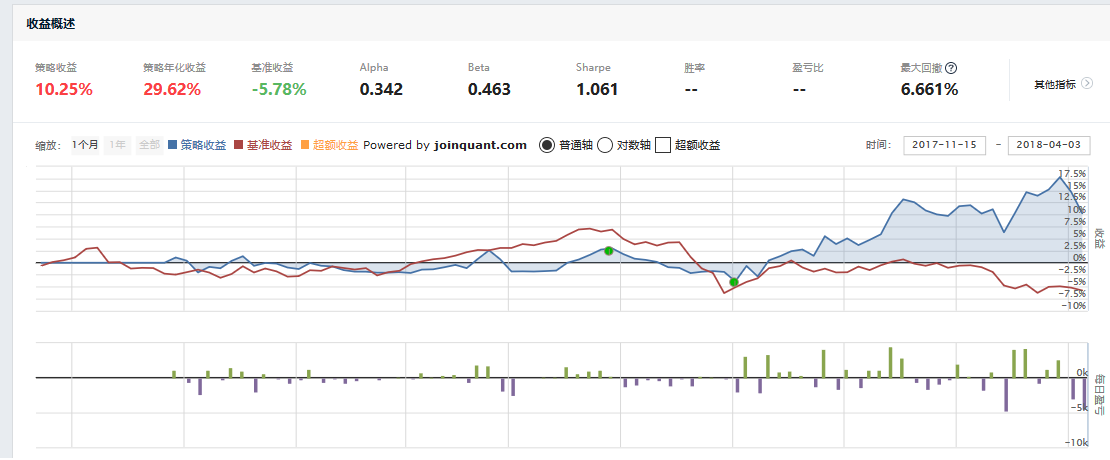
我的测试结果

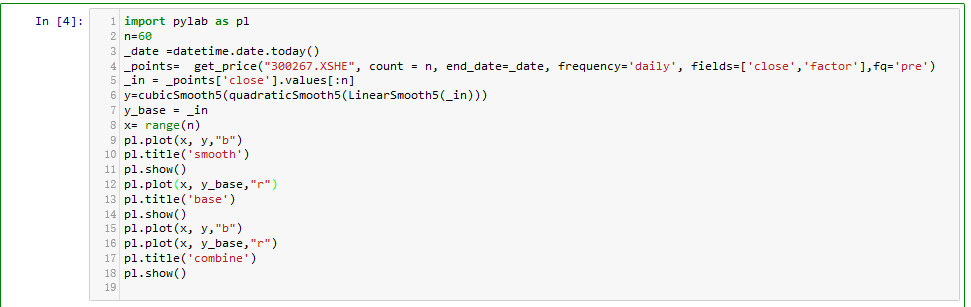
5.可以看到我截取了一段真实股价数据转换成了平滑曲线，其原本的数据是，base-原始数据的采集值   smooth-平滑后的数据（可以看到已经去掉了杂波[过高过低的股价数值]）  combine是原始采集值和平滑的对比

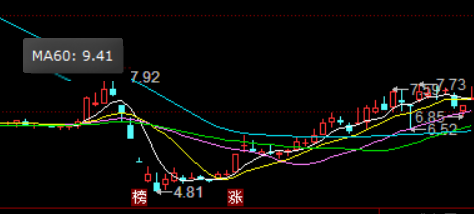
6.如图中平滑结果可以看出，这段波动股价的拐点有3处，由这个点可以分析出来何时买卖，当然这个结果还有很大优化的可能性。

7.拐点判断可以用一阶导数（中值定理）或者相邻点位数据差值加权平均方式
8.这张是我用加权平均方式找出买卖点的测试（还在优化中）
9.平滑函数python实现(2018-07-13 update)

def LinearSmooth5(inP):_outP = []
    n = len(inP)if n<5:for i in inP:
            _outP.append(i)else:
        _outP.append( ( 3.0 * inP[0]   2.0 * inP[1]   inP[2] - inP[4] ) / 5.0)
        _outP.append( ( 4.0 * inP[0]   3.0 * inP[1]   2 * inP[2]   inP[3] )/10.0)
        _i=0for i in  inP :if not _i == 0 and not _i==1 and not _i == n-2 and not _i ==n-1:
                _outP.append(( inP[_i - 2]   inP[_i - 1]   inP[_i]   inP[_i   1]   inP[_i   2] ) / 5.0)
            _i = _i 1_outP.append(( 4.0 * inP[n-1]   3.0 * inP[n - 2]   2 * inP[n - 3]   inP[n - 4] ) / 10.0)
        _outP.append(( 3.0 * inP[n-1]   2.0 * inP[n - 2]   inP[n - 3] - inP[n - 5] ) / 5.0    )return _outPdef quadraticSmooth5(inP):_outP = []
    n = len(inP)if n<5:for i in inP:
            _outP.append(i)else:
        _outP.append( ( 31.0 * inP[0]   9.0 * inP[1] -3.0* inP[2] - 5.0*inP[3] 3.0*inP[4] ) / 35.0)
        _outP.append( ( 9.0 * inP[0]   13.0 * inP[1]   12 * inP[2]   6.0*inP[3] - 5.0*inP[4] )/35.0)
        _i=0for i in  inP :if not _i == 0 and not _i==1 and not _i == n-2 and not _i ==n-1:
                _outP.append( ( - 3.0 * (inP[_i - 2]   inP[_i   2])   12.0 * (inP[_i - 1]   inP[_i   1])   17 * inP[_i] ) / 35.0)
            _i = _i 1_outP.append( ( 9.0 * inP[n - 1]   13.0 * inP[n - 2]   12.0 * inP[n - 3]   6.0 * inP[n - 4] - 5.0 * inP[n - 5] ) / 35.0)
        _outP.append(( 31.0 * inP[n - 1]   9.0 * inP[n - 2] - 3.0 * inP[n - 3] - 5.0 * inP[n - 4]   3.0 * inP[n - 5]) / 35.0)return _outPdef cubicSmooth5(inP):_outP = []
    n = len(inP)if n<5:for i in inP:
            _outP.append(i)else:
        _outP.append( (69.0 * inP[0]   4.0 * inP[1] - 6.0 * inP[2]   4.0 * inP[3] - inP[4]) / 70.0)
        _outP.append(  (2.0 * inP[0]   27.0 * inP[1]   12.0 * inP[2] - 8.0 * inP[3]   2.0 * inP[4]) / 35.0)
        _i=0for i in  inP :if not _i == 0 and not _i==1 and not _i == n-2 and not _i ==n-1:
                _outP.append(  (-3.0 * (inP[_i - 2]   inP[_i   2])  12.0 * (inP[_i - 1]   inP[_i   1])   17.0 * inP[_i] ) / 35.0)
            _i = _i 1_outP.append( (2.0 * inP[n - 5] - 8.0 * inP[n - 4]   12.0 * inP[n - 3]   27.0 * inP[n - 2]   2.0 * inP[n - 1]) / 35.0)
        _outP.append( (- inP[n - 5]   4.0 * inP[n - 4] - 6.0 * inP[n - 3]   4.0 * inP[n - 2]   69.0 * inP[n - 1]) / 70.0)return _outP