炒股的人对K线图一般都不陌生。我们平时见到的K线图都是以时钟为基准的,例如日线,周线,分钟线等等。每一根K线反映了单位时间内的价格信息。而量钟指的是相等成交量为划分单位组成的K线图。
举例而言,对于一只股票,如果经过1小时交易后价格从1元涨到2元,我们定义这一根60分钟的时钟线的开盘价open=1,收盘价close=2;如果经过100000交易量的冲击这只股票价格从1元涨到2元,那么我们定义这一根100000交易量的量钟线的开盘价open=1,收盘价close=2。下面我们采用中国平安2018年9月22日至2019年3月22日的数据来对比时钟线和量钟线的不同。
这里的时钟采用60分钟线,半年时间跨度里有464根K线,量钟取半年总交易量的464分之一,这样保证时钟图与量钟图总长度相同。由于K线数量多排列太过密集,这里取两张图的第41到101根进行分析。
时钟:
量钟:
这里可以看出,在第一波以62元为起点的拉升中,时钟图经过7根K线就到达了70元附近,而量钟图经历了13根K线才到达70元。接下来,在从70元顶点到60元低点的下跌中,量钟图同样耗费了更多根K线。也就是说,在这波62-70-60价格波动中,短时间内发生了巨额的交易量。量钟图比时钟图更详细刻画了这一波动过程中的价格变动。
那么相对于时钟图,量钟图能给我们带来哪些信息呢?还是以中国平安近半年数据中的收益率分布为例,传统的收益率以时钟为计量单位,常常呈现出尖峰厚尾的分布,也就是说相对于标准正态分布,时钟下的收益率数据极端值较多。由于价格常常是由成交量驱动的,相同的成交量对价格的冲击幅度存在一定上限,量钟下的收益率大大减少了极端值的发生,跟接近与正态分布,呈现出更好的统计学性质。
我们导入statsmodels库,对时钟和量钟下的收益率进行jarque-bera检验,也就是经典的正态性检验。时钟下的收益率分布的p-value为5.2907236529719751e-107,显然小于0.05,拒绝了样本来自正态总体的原假设,量钟下的收益率分布的p-value为0.073254565219318696,大于0.05,我们可以近似的认为该样本来自正态总体。
市场微观结构理论研究中,根据是否拥有信息优势,将交易者分为两种:知情交易者和非知情交易者。拥有信息的投资者会充分利用信息优势进行交易, 从而获取利润, 并导致股票价格的长期变化, 这类投资者被称为知情交易者(informed trader) , 完成的交易称为知情交易( informed trading) 。
非知情交易者没有信息的投资者因流动性等原因而进行交易, 只是导致股票价格产生暂时的波动, 不影响长期价格, 这类投资者被称为不知情交易者(uninformed trader) , 完成的交易称为不知情交易(uninformed trading)。
Easley and O’hara基于之前学者的一系列研究在2011年提出了 VPIN(Volume-Synchronized Probability of Informed Trading)即等交易量知情概率来度量高频环境下的信息不对称性,并称之为指令流毒性(Flow Toxicity)。那么如何估计知情交易概率呢?这就要用到上一部分中提到的量钟了。根据Easleyet al (2012)所推荐的Bulk Volume Classification(BVC)算法,首先将每天的成交量分成n等份交易篮子(Bulk),根据正态分布的概率估计方法将每份篮子的交易量划分为买和卖两部分,具体估计方法如下:
那么VPIN有什么用呢?Easleyet al (2011)指出在美股闪电崩盘之前市场的VPIN值巳经变得很高,这导致流动性提供者离开市场从而诱发大幅下跌 。周强龙、朱燕建和贾璐熙(2015)研究了“8·16”光大证券乌龙指事件当天沪深300股指期货市场的交易数据,发现2013年8月16日10点58分市场VPIN值开始急速攀升,随即主力合约价格也开始大幅上涨。事实上,根据后来的报道,乌龙指事件发生的当天上午光大证券策略投资部就开始做空股指期货进行套保,VPIN值高效反应了知情交易者的活动情况。总之,国内外大多数研究表明市场知情交易概率的升高将会恶化市场的流动性水平,使得市场后续更容易发生暴涨暴跌的极端走势。
本文采用单支股票第一个交易日总交易量的50分之一作为每个交易篮子的交易量,采用的高频数据来自tushare数据库,频率达到3秒级别,这样每个交易日可以4000多个数据,基本保证每个交易篮子交易量相等。
接下来采用4支股票作为案例,数据均来自2018年6月至2019年3月。为了方便对比,选了两只大盘股:贵州茅台,工商银行,两只小盘股(同时也是最近炒作比较厉害的两只妖股):东方通信,市北高新。
这里我们可以发现,两只妖股在连续涨停板拉升之前呈现出较高vpin水平,说明主力在拉升前提前执行了大量知情交易,而在连板后vpin水平明显下降,说明此时有大量非知情交易者参与到股票交易中。其中东方通信在拉升前知情交易概率一度达到0.9的极高水平。
东方通信:
市北高新在第一波连板VPIN显著下降后,在样本期的第150个交易日左右VPIN又达到第二个峰值,随后开始了第二波拉升。
市北高新:
而工商银行和贵州茅台在整个样本期VPIN峰值都没超过0.6的水平,基本呈现震荡走势,说明这两支股票的知情交易现象并不明显,由于盘子太大,很少有主力来这里操纵价格走势。
工商银行:
贵州茅台: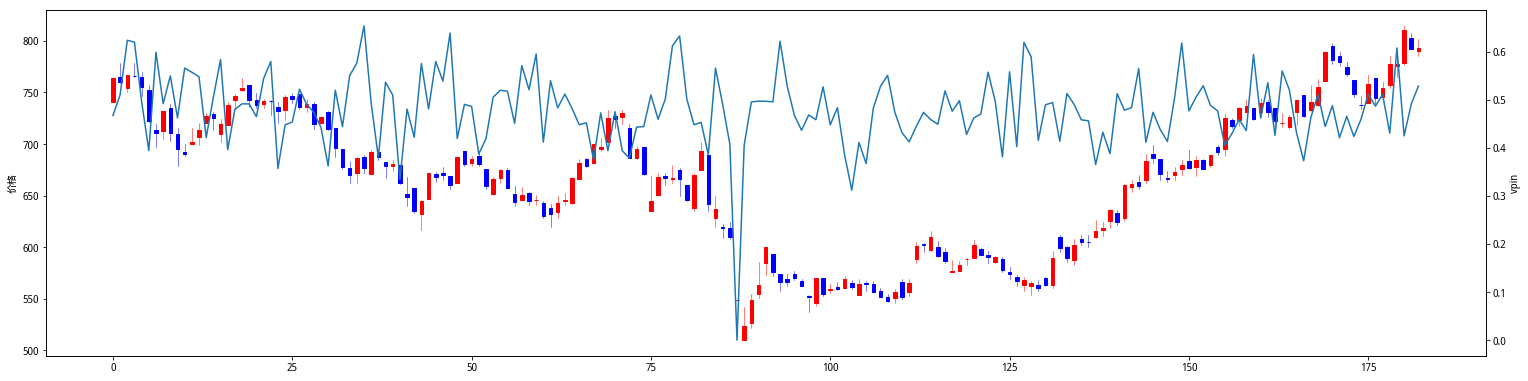
参考文献:
Easley, D., Lopez de Prado, M., O’Hara, M., 2012.“Flow Toxicity and Liquidity in a High-frequency World”. Review
of Financial Studies 25(5): 1457–1493.
Easley, D., Lopez de Prado, M., O’Hara, M., 2011a.“The exchange of flow toxicity”. Journal of Trading .6 (2), 8–13.
周强龙、朱燕建和贾璐熙,《市场知情交易概率、流动性与波动性:来自中国股指期货市场的经验证据》,《金融研究》2015第5期,第132~147页
炒股的人对K线图一般都不陌生。我们平时见到的K线图都是以时钟为基准的,例如日线,周线,分钟线等等。每一根K线反映了单位时间内的价格信息。而量钟指的是相等成交量为划分单位组成的K线图。
举例而言,对于一只股票,如果经过1小时交易后价格从1元涨到2元,我们定义这一根60分钟的时钟线的开盘价open=1,收盘价close=2;如果经过100000交易量的冲击这只股票价格从1元涨到2元,那么我们定义这一根100000交易量的量钟线的开盘价open=1,收盘价close=2。下面我们采用中国平安2018年9月22日至2019年3月22日的数据来对比时钟线和量钟线的不同。
#加载需要的库
from math import *
from jqdata import *
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.finance as mpf
import tushare as ts
import statsmodels.stats.stattools
#定义画K线图的函数
def drawkline(data):
prices = data[['open', 'high', 'low', 'close']]
dates = data.index
candleData = np.column_stack([list(range(len(dates))), prices])
fig = plt.figure(figsize=(25, 8))
ax = fig.add_axes([0.1, 0.3, 0.8, 0.6])
mpf.candlestick_ohlc(ax, candleData, width=0.5, colorup='r', colordown='b')
plt.show()
#收集时钟线数据
timeline=get_price('601318.XSHG', start_date='2018-09-22', end_date='2019-03-22', frequency='60m', fields=None, skip_paused=False, fq='pre', count=None)
#收集量钟线的数据
day=get_price('601318.XSHG', start_date='2018-09-22', end_date='2019-03-22', frequency='minute', fields=None, skip_paused=False, fq='pre', count=None)
bulkvol=day['volume'].sum()/len(timeline)
day['volcum']=day['volume'].cumsum()
day['number']=day['volcum']//bulkvol
n=int(max(day['number']))
volkline=pd.DataFrame(columns=('number','open','close','high','low','vol','change'))
for j in range(0,n):
bulk = day[day['number'] == j]
change=(bulk.iloc[-1]['close']/bulk.iloc[0]['open'])-1
Open=bulk.iloc[0]['open']
Close=bulk.iloc[-1]['close']
vol=bulk['volume'].sum()
high=max(bulk['high'])
low=min(bulk['low'])
volkline=volkline.append(pd.DataFrame({'change':[change],'high':[high],'low':[low],'number':[j],'open':[Open],'close':[Close],'vol':[vol]}),ignore_index=True)
这里的时钟采用60分钟线,半年时间跨度里有464根K线,量钟取半年总交易量的464分之一,这样保证时钟图与量钟图总长度相同。由于K线数量多排列太过密集,这里取两张图的第41到101根进行分析。
#半年,时钟图
drawkline(timeline)
#量钟图
drawkline(volkline)
这里可以看出,在第一波以62元为起点的拉升中,时钟图经过7根K线就到达了70元附近,而量钟图经历了13根K线才到达70元。接下来,在从70元顶点到60元低点的下跌中,量钟图同样耗费了更多根K线。而从60元低点到67元的这一波反弹中,量钟图只耗费了4根K线,时钟图则耗费了20多根K线。
这说明,在第一波62-70-60价格波动中,短时间内发生了巨额的交易量,在第二波60-67的反弹中,很长一段时间只发生了极少的交易量。
#时钟
drawkline(timeline[40:100])
#量钟
drawkline(volkline[40:100])
那么相对于时钟图,量钟图能给我们带来哪些信息呢?还是以中国平安近半年数据中的收益率分布为例,传统的收益率以时钟为计量单位,常常呈现出尖峰厚尾的分布,也就是说相对于标准正态分布,时钟下的收益率数据极端值较多。由于价格常常是由成交量驱动的,相同的成交量对价格的冲击幅度存在一定上限,量钟下的收益率大大减少了极端值的发生,跟接近与正态分布,呈现出更好的统计学性质。
timeline['change']=(timeline['close']/timeline['open'])-1
plt.hist(timeline['change'], bins=len(timeline), edgecolor="black", alpha=0.7)
plt.ylabel('涨跌幅度')
plt.title('时钟下的涨跌幅度分布,尖峰厚尾')
plt.show()
plt.hist(volkline['change'], bins=len(timeline), edgecolor="black", alpha=0.7)
plt.title('量钟下的涨跌幅度分布,近似正态')
plt.ylabel('涨跌幅度')
plt.show()
这里我们导入statsmodels库,对时钟和量钟下的收益率进行jarque-bera检验,也就是经典的正态性检验。时钟下的收益率分布的p-value为5.2907236529719751e-107,显然小于0.05,拒绝了样本来自正态总体的原假设,量钟下的收益率分布的p-value为0.073254565219318696,大于0.05,我们可以近似的认为该样本来自正态总体。
time=statsmodels.stats.stattools.jarque_bera(timeline['change'], axis=0)[1]
vol=statsmodels.stats.stattools.jarque_bera(volkline['change'], axis=0)[1]
print(time,vol)
(5.2907236529719751e-107, 0.073254565219318696)
市场微观结构理论研究中,根据是否拥有信息优势,将交易者分为两种:知情交易者和非知情交易者。拥有信息的投资者会充分利用信息优势进行交易, 从而获取利润, 并导致股票价格的长期变化, 这类投资者被称为知情交易者(informed trader) , 完成的交易称为知情交易( informed trading) 。
非知情交易者没有信息的投资者因流动性等原因而进行交易, 只是导致股票价格产生暂时的波动, 不影响长期价格, 这类投资者被称为不知情交易者(uninformed trader) , 完成的交易称为不知情交易(uninformed trading)。
Easley and O’hara基于之前学者的一系列研究在2011年提出了 VPIN(Volume-Synchronized Probability of Informed Trading)即等交易量知情概率来度量高频环境下的信息不对称性,并称之为指令流毒性(Flow Toxicity)。那么如何估计知情交易概率呢?这就要用到上一部分中提到的量钟了。根据Easleyet al (2012)所推荐的Bulk Volume Classification(BVC)算法,首先将每天的成交量分成n等份交易篮子(Bulk),根据正态分布的概率估计方法将每份篮子的交易量划分为买和卖两部分,具体估计方法如下: $$V^{buy}=V*Z(\frac{P_{i}-P_{i-1}}{\sigma}) $$ $$V^{sell}=V-V^{buy} $$ 其中Z是标准正态分布的累积分布函数,∆P/σ表示篮子内价格变化除以标准差将其标准化,V为每份篮子的交易量,其基本思想就是价格上涨时赋予买方更多的成交量权重,下跌时赋予卖方更多的权重,当篮子内价格没有变化时则买卖交易量相等。通过计算所有篮子内的买卖交易量,可以得出这一天的vpin值: $$VPIN=\frac{1}{n}\sum_{i=1}^{n}\frac{\left |V_{i}^{sell}-V_{i}^{buy} \right |}{V_{i}}$$ 从推导的公式我们可以发现,vpin值实质是度量了交易量的方向特征,如果某一天市场参与者大部分是非知情交易者,那么他们的交易方向都带有随机性,每个等量交易篮子内的买卖量差异不大,这一天的vpin水平就会很低。如果某一天市场参与者出现了许多知情交易者,也就是我们常说的主力,当他们对价格进行拉抬或者打压,这些交易行为就会使每个等量交易篮子具有明确的买卖方向,这一天的vpin水平就会很高。
那么VPIN有什么用呢?Easleyet al (2011)指出在美股闪电崩盘之前市场的VPIN值巳经变得很高,这导致流动性提供者离开市场从而诱发大幅下跌 。周强龙、朱燕建和贾璐熙(2015)研究了“8·16”光大证券乌龙指事件当天沪深300股指期货市场的交易数据,发现8月16日10点58分市场VPIN值开始急速攀升,随即主力合约价格也开始大幅上涨。事实上,根据后来的报道,乌龙指事件发生的当天上午光大证券策略投资部就开始做空股指期货进行套保,VPIN值高效反应了知情交易者的活动情况。总之,国内外大多数研究表明市场知情交易概率的升高将会恶化市场的流动性水平,使得市场后续更容易发生暴涨暴跌的极端走势。
本文采用单支股票第一个交易日总交易量的50分之一作为每个交易篮子的交易量,由于jqdata仅提供分钟级的交易数据,本文采用的高频数据来自tushare数据库,频率达到3秒级别,这样每个交易日可以4000多个数据,基本保证每个交易篮子交易量相等。
ts.get_tick_data('000001',date='2019-03-26',src='tt').head()
| time | price | change | volume | amount | type | |
|---|---|---|---|---|---|---|
| 0 | 09:25:04 | 12.23 | 0.12 | 8713 | 10655999 | 卖盘 |
| 1 | 09:30:04 | 12.22 | -0.01 | 7168 | 8761907 | 卖盘 |
| 2 | 09:30:06 | 12.23 | 0.01 | 978 | 1196164 | 买盘 |
| 3 | 09:30:09 | 12.25 | 0.02 | 1630 | 1996327 | 买盘 |
| 4 | 09:30:12 | 12.25 | 0.00 | 1164 | 1426453 | 买盘 |
#vpin计算,其中start,end为时间,code为股票代码,注意tushare的高频数据最早到2018年6月
def vpin(start,end,code):
tradeday=get_trade_days(start_date=start,end_date=end)
firstday = ts.get_tick_data(code,date=str(tradeday[0]),src='tt')
firstdayvol=firstday['volume'].sum()
bulkvol=firstdayvol/50
result=pd.DataFrame(columns=('date','vpin','high','low','open','close'))
datelist = []
allchange=[]
for i in tradeday:
day = ts.get_tick_data(code,date=str(i),src='tt')
if day is not None:
day['volcum']=day['volume'].cumsum()
day['number']=day['volcum']//bulkvol
n=int(max(day['number']))
for j in range(0,n):
bulk = day[day['number'] == j]
if len(bulk)>0:
change=(bulk.iloc[-1]['price']/bulk.iloc[0]['price'])-1
allchange.append(change)
std=np.std(np.array(allchange))
for i in tradeday:
day = ts.get_tick_data(code,date=str(i),src='tt')
if day is not None:
chglist=[]
vpinlist=[]
day['volcum']=day['volume'].cumsum()
day['number']=day['volcum']//bulkvol
n=int(max(day['number']))
high=max(day['price'])
low=min(day['price'])
Open=day['price'].iloc[0]
Close=day['price'].iloc[-1]
for j in range(0,n):
bulk = day[day['number'] == j]
if len(bulk)>0:
change=(bulk.iloc[-1]['price']/bulk.iloc[0]['price'])-1
chglist.append(change)
for change in chglist:
z=(change)/std
p=(1.0 + erf(z / sqrt(2.0))) / 2.0
vpinlist.append(abs(((1-p)-p)))
vpin=np.mean(np.array(vpinlist))
result=result.append(pd.DataFrame({'date':[i],'vpin':[vpin],'high':[high],'open':[Open],'low':[low],'close':[Close]}),ignore_index=True)
return result
#画图函数
def drawline(data):
prices = data[['open', 'high', 'low', 'close']]
dates = data.index
candleData = np.column_stack([list(range(len(dates))), prices])
fig = plt.figure(figsize=(25, 8))
ax1 = fig.add_axes([0.1, 0.3, 0.8, 0.6])
mpf.candlestick_ohlc(ax1, candleData, width=0.5, colorup='r', colordown='b')
ax2 = ax1.twinx()
ax2.plot(dates, data['vpin'])
ax1.set_ylabel('价格')
ax2.set_ylabel('vpin')
plt.show()
#由于高频数据量大,程序运行时间较长
dftx=vpin('2018-06-20','2019-03-20','600776')
sbgx=vpin('2018-06-20','2019-03-20','600604')
gzmt=vpin('2018-06-20','2019-03-20','600519')
gsyh=vpin('2018-06-20','2019-03-20','601398')
接下来采用4支股票作为案例,数据均来自2018年6月至2019年3月。为了方便对比,选了两只大盘股:中国平安,工商银行,两只小盘股(同时也是最近炒作比较厉害的两只妖股):东方通信,市北高新。
这里我们可以发现,两只妖股在连续涨停板拉升之前呈现出较高vpin水平,说明主力在拉升前提前执行了大量知情交易,而在连板后vpin水平明显下降,说明此时有大量非知情交易者参与到股票交易中。其中东方通信在拉升前知情交易概率一度达到0.9的极高水平,市北高新在第一波连板VPIN显著下降后,在样本期的第150个交易日左右VPIN又达到第二个峰值,随后开始了第二波拉升。
#东方通信
drawline(dftx)
#市北高新
drawline(sbgx)
而工商银行和贵州茅台在整个样本期VPIN峰值都没超过0.6的水平,说明这两支股票的知情交易现象并不明显,由于盘子太大,很少有主力来这里操纵价格走势。
#工商银行
drawline(gsyh)
#贵州茅台
drawline(gzmt)
参考文献:
Easley, D., Lopez de Prado, M., O’Hara, M., 2012.“Flow Toxicity and Liquidity in a High-frequency World”. Review of Financial Studies 25(5): 1457–1493.
Easley, D., Lopez de Prado, M., O’Hara, M., 2011a.“The exchange of flow toxicity”. Journal of Trading .6 (2), 8–13.
周强龙、朱燕建和贾璐熙,《市场知情交易概率、流动性与波动性:来自中国股指期货市场的经验证据》,《金融研究》2015第5期,第 132~147页

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
