导语:kd 树是一种二叉树数据结构,可以用来进行高效的 kNN 计算。kd 树算法偏于复杂,本篇将先介绍以二叉树的形式来记录和索引空间的思路,以便读者更轻松地理解 kd 树。
阅读本文之前请掌握 kNN(level-1)的知识。
前言
kd 树(k-dimensional tree)是一个包含空间信息的二项树数据结构,它是用来计算 kNN 的一个非常常用的工具。如果特征的维度是 DD
D
,样本的数量是 NN
N
,那么一般来讲 kd 树算法的复杂度是 O(DlogN)O(Dlog?N)
O (D\log N)
,相比于穷算的 O(DN)O(DN)
O(D N)
省去了非常多的计算量。
因为 kd 树的概念和算法较为复杂,固将本教程分为“思路篇”和“详细篇”。两篇的内容在一定程度上是重叠的,但是本篇注重于讲解 kd 树背后的思想和直觉,告诉读者一颗二项树是如何承载空间概念的,我们又该如何从树中读取这些信息;而之后的详细篇则详细讲解 kd 树的定义,如何构造它并且如何计算 kNN。出于教学起见,本文讲的例子和算法与严格的 kd 树有一些差异。有算法经验或者想尝试挑战的读者可以直接跳过本篇去读详细篇。
关于在学习编程和算法时有没有必要自己制作轮子的问题,一直存在着很多的争议。作者认为,做不做轮子暂且不论,但是有必要去了解轮子是怎么做出来的。Python 的 scikit-learn 机器学习包提供了蛮算、kd 树和 ball 树三种 kNN 算法,学完本篇的读者若无兴趣自撰算法,可以非常轻松地使用该包,详细可见 scikit-learn 之 kNN 分类。
直觉
给定一堆已有的样本数据,和一个被询问的数据点(红色五角星),我们如何找到离五角星最近的15个点?
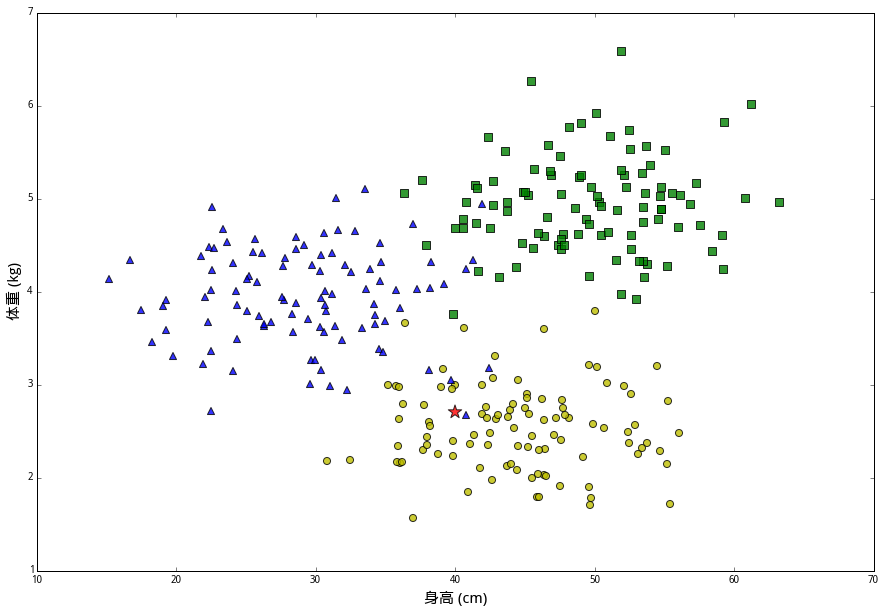
先忽略在编程上的实现,想一想一个人如何主观地执行。嗯,他一定会把在五角附近的一些点中,分别计算每一个的距离,然后选最近的15个。这样可能只需要进行二三十次距离计算,而不是300次。
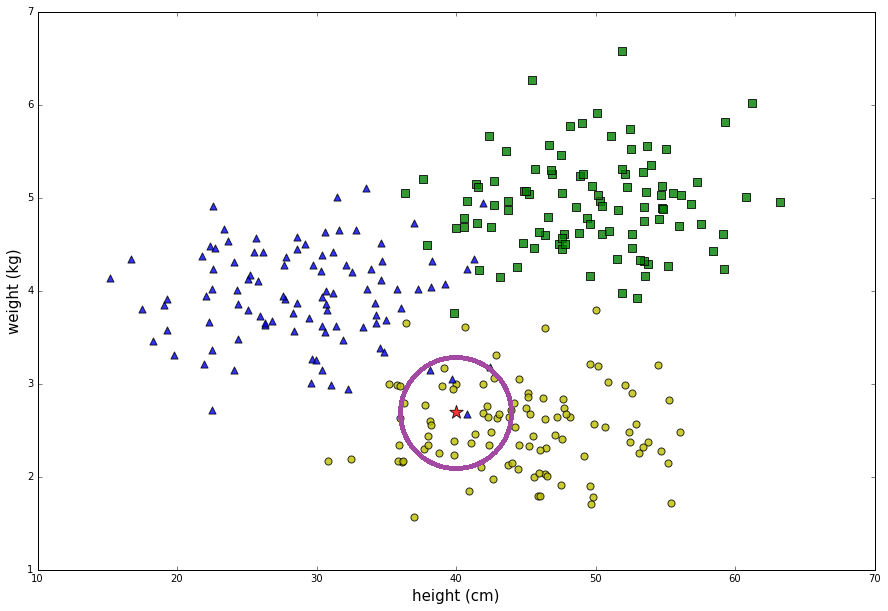
如图,只对紫圈里的点进行计算。
啊哈!问题来了。我们讲到的“附近”已经包含了距离的概念,如果不经过计算我们怎么知道哪个点是在五角星的“附近”?为什么我们一下就认出了“附近”而计算机做不到?那是因为我们在观看这张图片时,得到的输入是已经带有距离概念的影像,然而计算机在进行计算时得到的则是没有距离概念的坐标数据。如果要让一个人人为地从300组坐标里选出最近的15个,而不给他图像,那么他也省不了功夫,必须要把300个全部计算一遍才行。
这样来说,我们要做的就是在干巴巴的坐标数据上进行加工,将空间分割成小块,并以合理地方法将信息进行储存,这样方便我们读取“附近”的点。
切割
这只危险的兔子,它又回来了!它今天上了四个纹身,爱心、月牙、星星和眼泪,下面是它的照片。

我们来回答一个简单的问题:在这幅照片上,距离爱心最近的纹身是什么?记得上一篇文章中,我们选用的特征是每一只兔子的身高和体重;这次就不一样了,在这个问题中,每个纹身的特征是照片平面上的横轴和竖轴的坐标。
对于这个问题,如果进行蛮算的办法我们需要计算 3 次距离(分别和月亮、眼泪和星星算一次)。下面我们要做的是把整个空间按照左右和上下进行等分,并且把分割后的小空间以二叉树形式进行记录,这样可以很快地读取邻近的点而省去计算量。
好,我们先竖向沿中间把这个兔子切成两半

再沿横向从中间切成四份

再沿着竖向平分八份
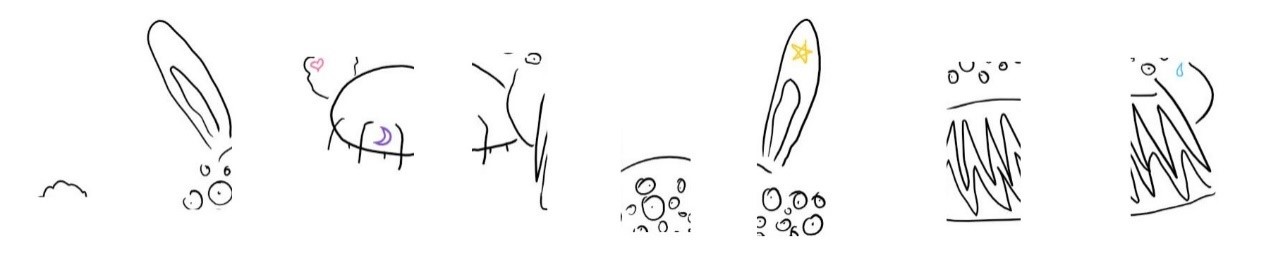
最后再沿横向切一次。这次有些区域是完全空白的,我们就把它舍弃不要了,得到 14 份:

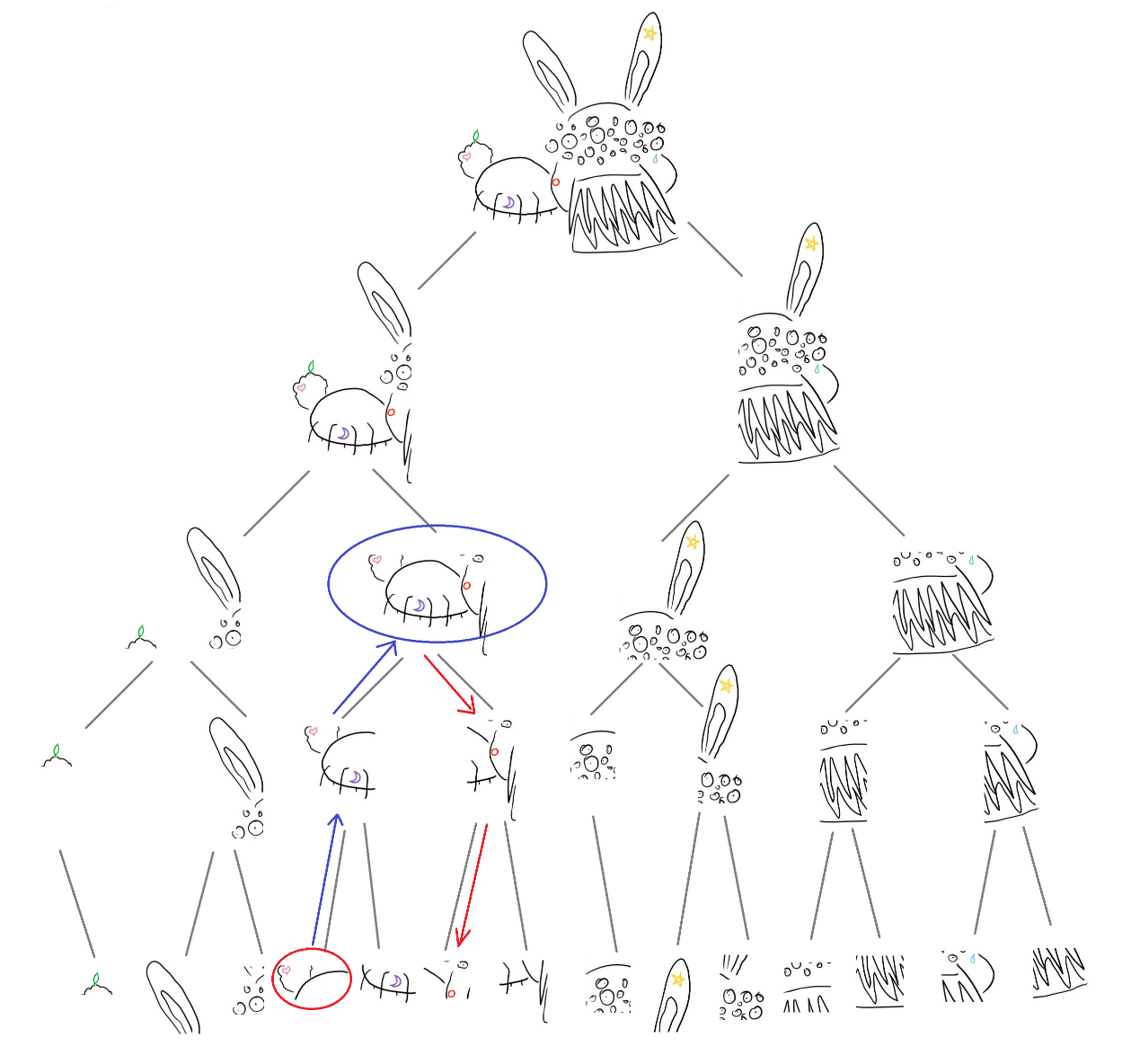
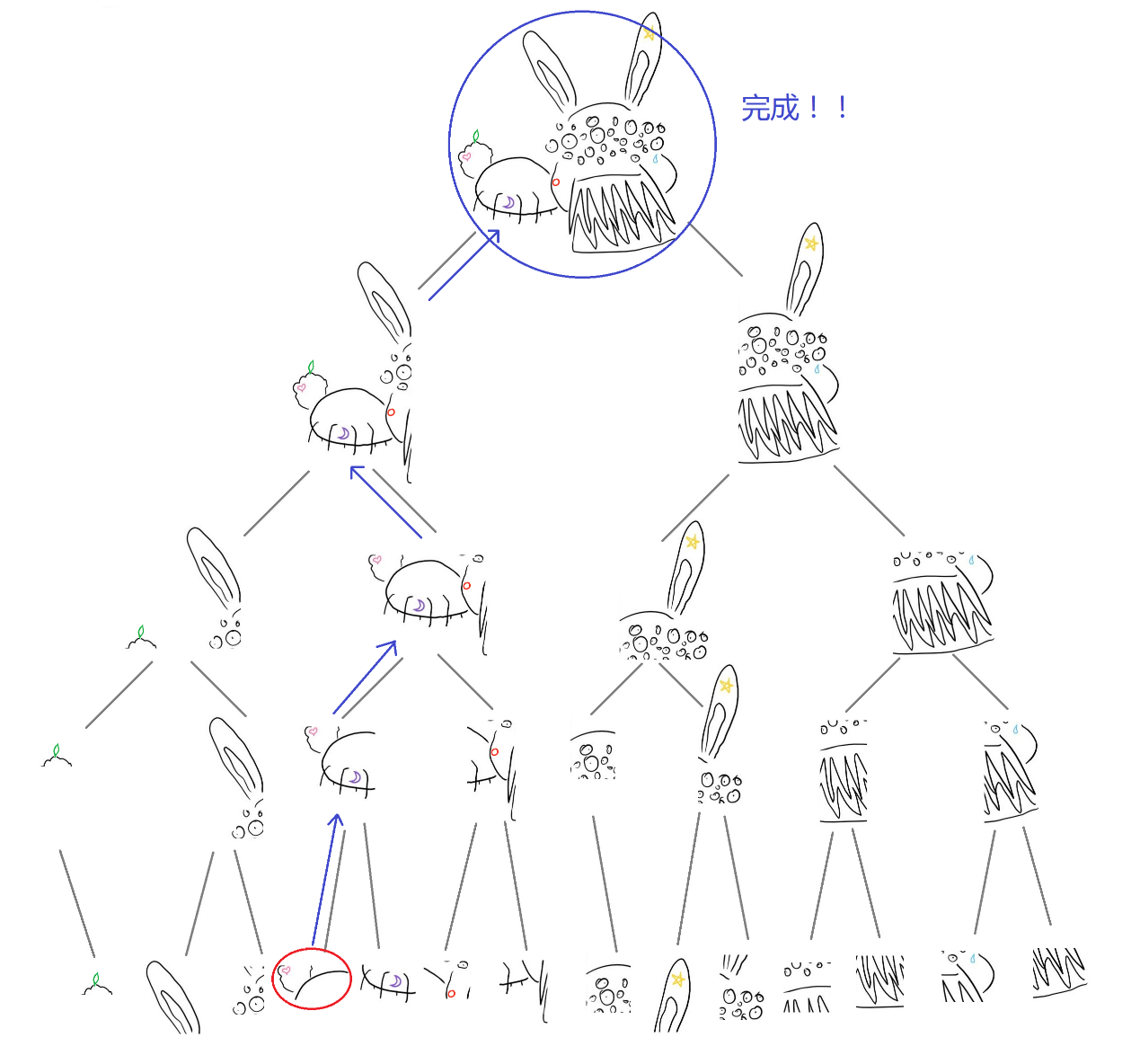
我们再按照上下左右的关系把切开的图片做成一个二叉树,树的每一个节点是一幅图,它的两个枝是这幅图平分出来的子图。
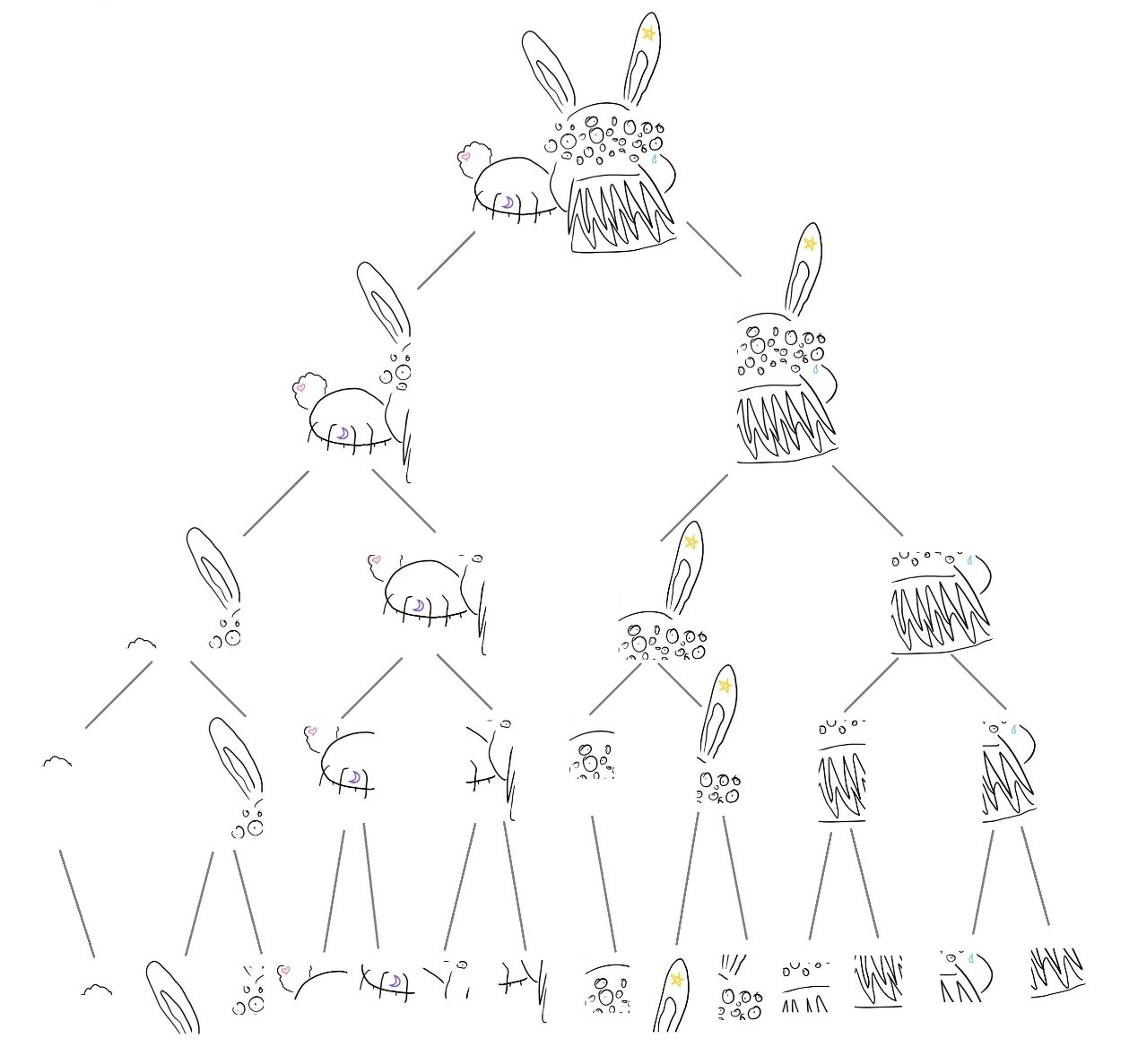
可以看出这个树状结构包含了很多局部性的信息,因为它的每一个节点都是按照上下或者左右进行平分的,因此如果两个点在树中的距离较近,那么它们的实际距离就是比较近的。
搜寻
接下来我们要通过这棵二叉树找到离爱心最近的纹身。
首先从树的最顶端开始,向下搜寻找到最底部包含爱心的节点。这个操作非常简单,因为每一次分割要么是沿着某纵线 x=ax=a
x=a
要么是沿着横线 y=ay=a
y=a
,因此只需要判断爱心的 xx
x
或 yy
y
轴坐标是大于 aa
a
还是小于 aa
a
,便知道是向左还是右边选择树枝。
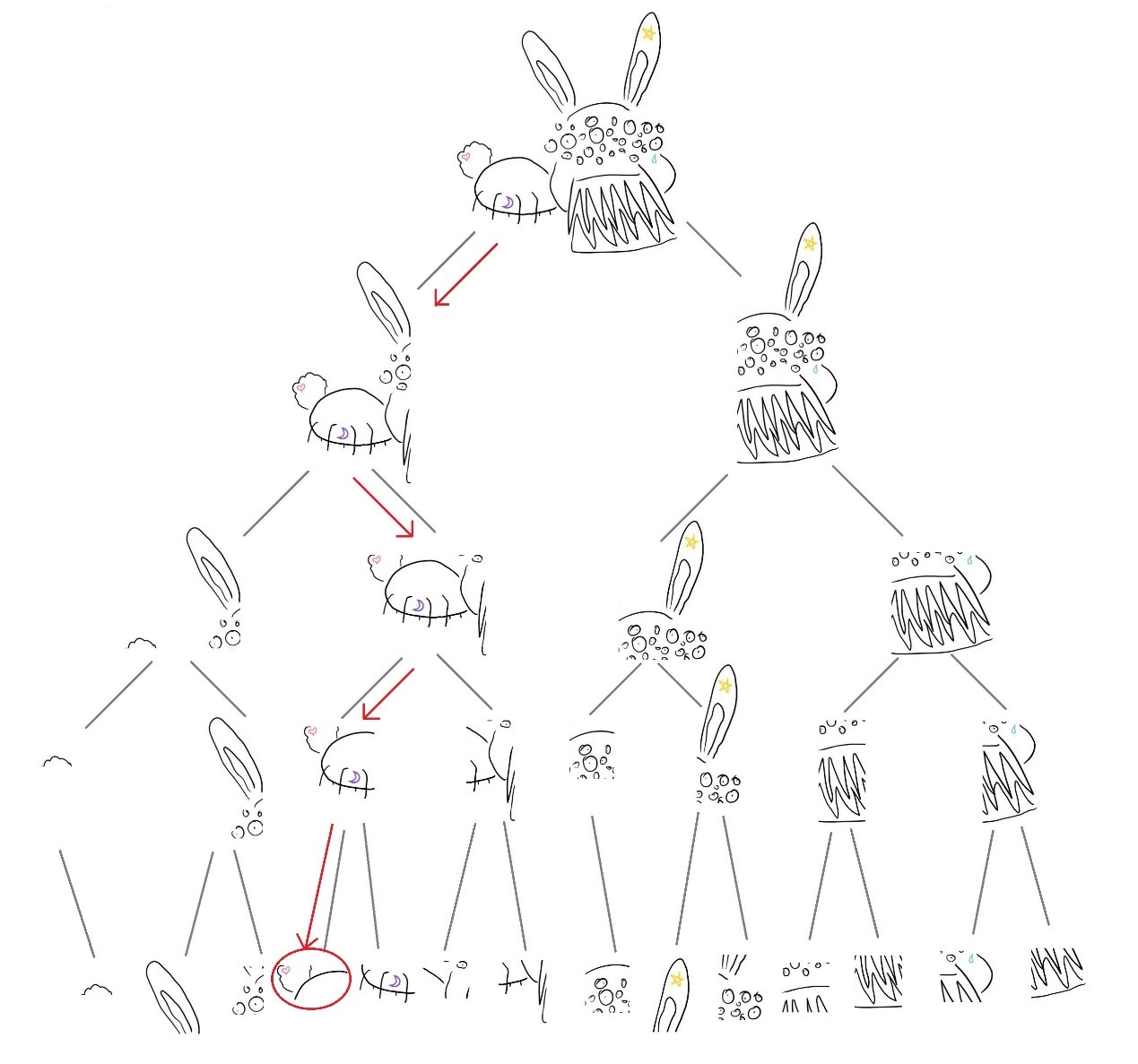
在找到了爱心之后,我们沿着相同的路径向上攀爬。只爬了一节就发现了屁股上的两个纹身

这里看出,在8平分的情况下,爱心和月亮是在同一个区域的。在某种意义上来讲它们是“近”的,但是我们还不能确定它们是最近的,因此还要继续向上攀爬寻找。再继续向上爬两个节点,都没有出现爱心和月亮以外的纹身。在下面这个节点中
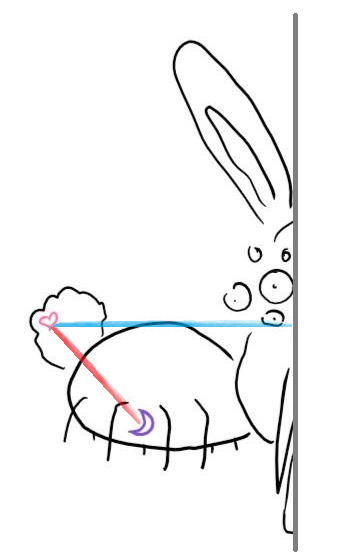
我们发现爱心和月亮之间的距离(红线)要小于爱心和分割线的距离(蓝线),也就是说,不论分割线的右边是什么情况,那边的纹身都不可能离爱心更近。因此可以判断,离爱心最近的图形是月亮。
这样,我们只计算了一次爱心和月亮之间的距离和一次爱心和分割线之间的距离,而不是分别计算爱心和其他三个纹身的距离。并且,要知道,爱心和分割线之间距离的计算非常简单,就是爱心的 xx
x
坐标和分割线的 xx
x
坐标的差(的绝对值),相比于计算两点之间的距离
((x1?y1)2 (x2?y2)2)????????????????????√((x1?y1)2(x2?y2)2)
\sqrt{((x_1-y_1 )^2 (x_2-y_2 )^2 )}
要省下很多计算量。
麻烦
啊,但也有可能这个搜寻最近点的过程没那么顺利。在上面的计算中,在找到了离爱心比较近的月亮之后,我们发现爱心距离分割线的距离比较远,因此确定月亮的确就是最近的。但是,在分割线的另一边有一个更近的纹身,那么情况就稍微复杂了。
就说这个兔子啊,又去加了两个纹身,一片叶子和一个圆圈。

二叉树分割上也相应地多出这两个纹身。我们想找到离爱心最近的纹身,所以依旧向下搜寻先找到爱心。
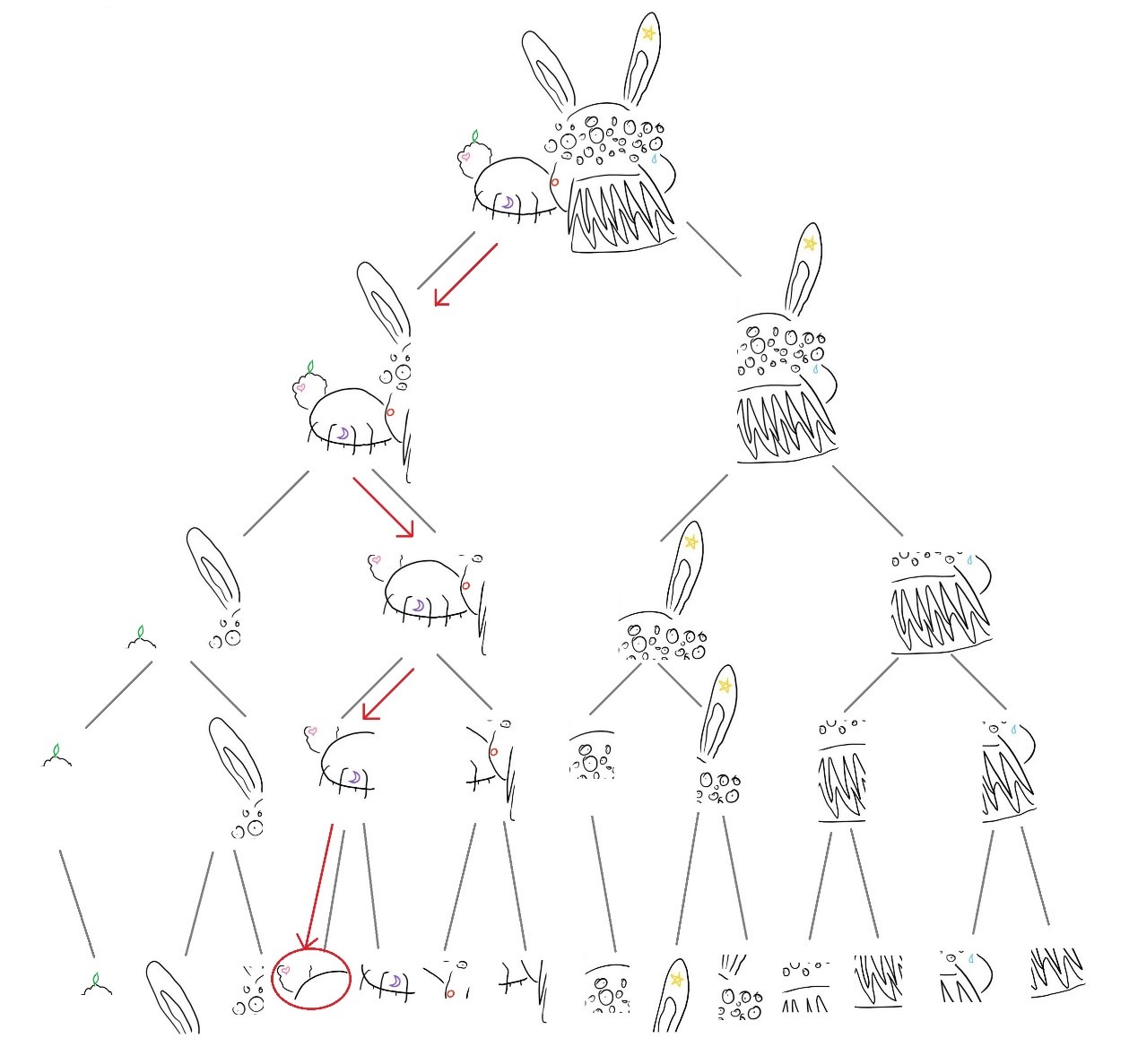
我们找来一张纸,记下在已访问节点中距离爱心最近的纹身和所对应的距离。现在这张纸还是空的。
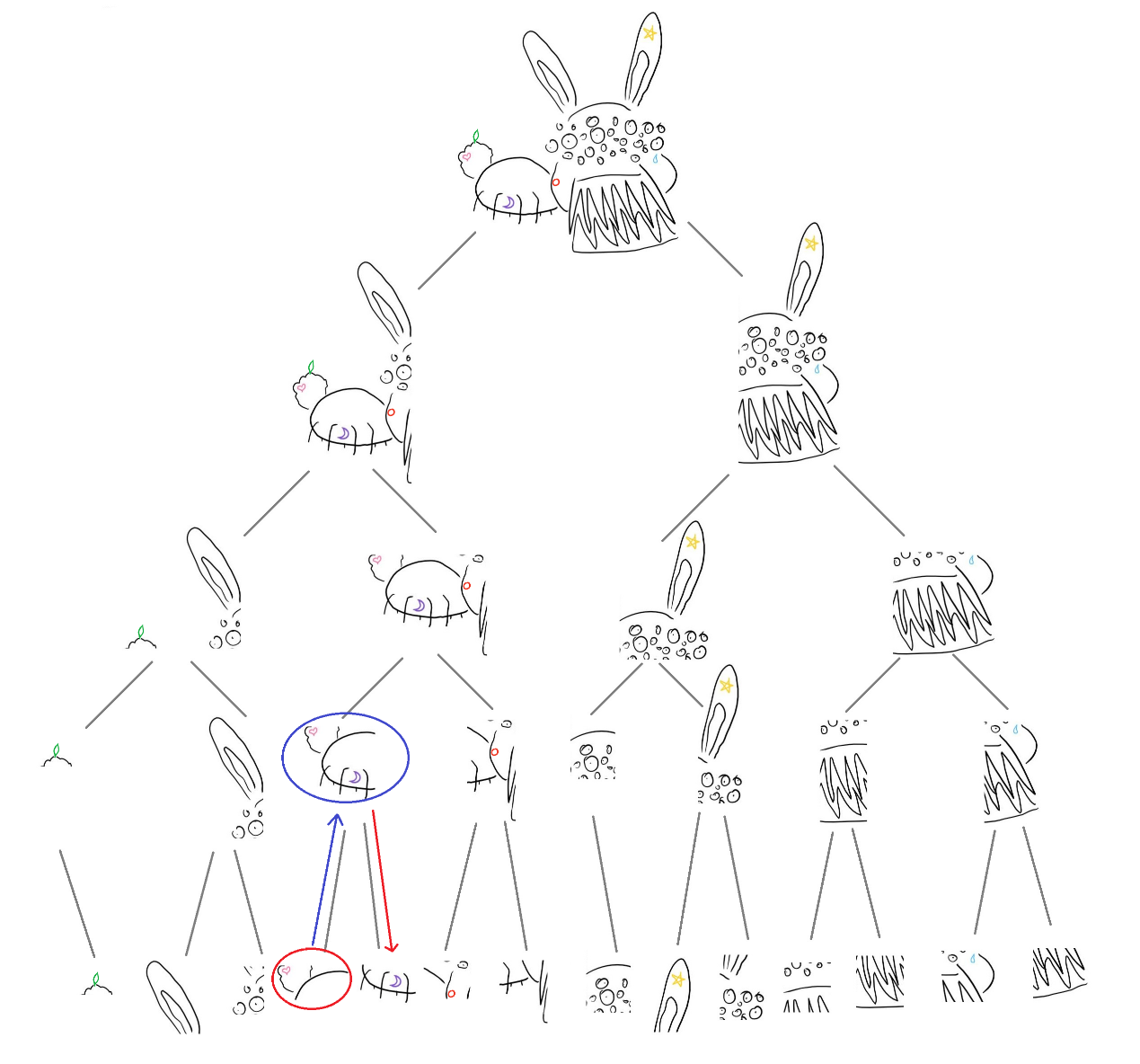
向上爬了一节,发现那一节的另一个枝里有月亮,于是跑下去查看月亮的坐标,计算爱心和月亮的距离,并在纸上记录 (图形=月亮,距离=d1)(图形=月亮,距离=d1)
(图形=月亮,距离=d_1)
。
再回到蓝圈的节点向上爬,继续向上爬。我们发现,d1d1
d_1
(红线)大于爱心和分割线的距离(蓝线)。
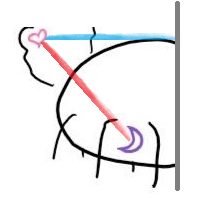
也就是说分割线的另一边可能有更近的点,所以从另一个分枝开始向下搜,找到…
在另一个分枝中我们追溯到圆圈,并计算它与爱心的距离 d2d2
d_2
,发现 d2>d1d2>d1
d_2>d_1
,比月亮远,所以丢弃不要。
再向上爬一个节,我们发现 d1d1
d_1
(红线)大于爱心和切分线之间的距离(蓝线)
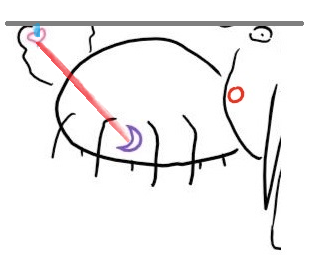
因此,切分线的另一端可能有更近的纹身,因此我们从另一个树枝向下搜索…

找到了叶子。(所幸在这个分枝里只搜索到了叶子,如果有更多的图形的话,还需要进行多层的递归。具体的过程会在后面的详细篇中讲解。)计算叶子和爱心之间的距离,得 d3d3
d_3
,并发现 d3<d1d3<d1
d_3\lt d_1
,比月亮更近,于是更新纸上的记录为 (纹身=叶子,距离=d3)(纹身=叶子,距离=d3)
(\text{纹身}=\text{叶子},\text{距离}=d_3)
。
再向上攀登一节,我们发现 d3d3
d_3
小于爱心和切分线的距离,因此另一边的数据就不用考虑了。
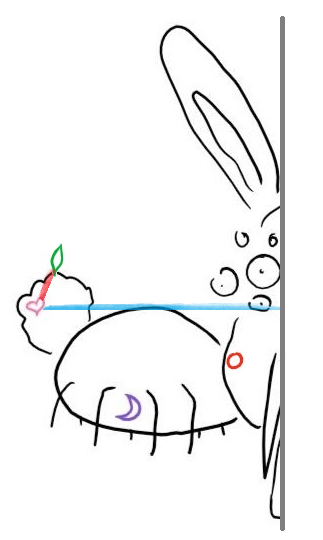
这次我们已经爬到了树的最顶端,完成了搜索,纸上记载的 (叶子,d3)(叶子,d3)
(叶子,d_3)
就是最近的纹身和对应的距离。
结语
在以上的算法中,当我们已经找到了比切分线更近的点时,就不需要继续搜索切分线另一边的点了,因为那些只会更远。于是,通过把整个空间进行分割并以树状结构进行记录,我们只需要在问题点附近的一些区域进行搜寻便可以找到最近的数据点,节省了大量的计算。
到此为止,本篇文章友好地介绍了如何使用二叉树的形式记录距离信息并快速地进行搜索,但文中所讲的还不是 kd 树。下一篇文章,kd 树算法之详细篇,将系统性地介绍 kd 树的定义和在 kd 树上的 kNN 算法。