请　[注册]　或　[登录]　 | 返回主站

量化交易吧 /  数理科学 帖子：3364762 新帖：0

拉布谢尔资金管理系统的统计学验证

螺罗丝发表于：4 月 17 日 20：13回复(1)

有三种谎言: 谎言, 可恶的谎言, 以及统计.

简介

在很多周末, 我都在深度浏览互联网, 偶然间我碰到了一个之前从来没有听说过的资金管理系统. 它被称为拉布谢尔, 或者取消系统(使用拉布谢尔的外汇交易真空清除系统, 俄语版). 英文版描述可以在这里找到. 此系统是马丁格尔的变种, 因为您在失误以后需要加大您的投注然后在获利中小赢. 然而,它是一个不大激进的版本, 因为下注并非双倍, 而是增加一定数量.

下面这些段落描述了让我非常好奇的系统属性:

  • "所以, 请注意获利交易的数量应该超过33-40%, 这样才能保证此系统正常工作并获利!!!"  – 这是非常重要的说明. 然而, 为什么初始百分比范围如此之大并不清楚 – 从 33% 到 40%.

  • "记住, 这种方法可以认为是游戏场中的欺骗性阴谋".  –  真的吗?那么, 它真的能有用?!

  • "但是原则还是一样的 – 获胜 33% 可以抵消 66% 的失败. 所以, 如果您在实际外汇交易中应用此资金管理方法的话, 您需要一个获胜几率在50%以上并且利润因子>=1的系统".

实际上, 提到的文章声明了您需要一个输赢数量差不多的系统, 胜率大约是50%(或者说"比33%要多"). 如果您有这样一个系统, 拉布谢尔方法可以很容易使您盈利!所以, 既然我们有方法把它应用到不错的领域, 我们还有必要去寻找其他的数学方法吗?毕竟, 开发一个取胜率47%的系统应该并不难...

让我们看看拉布谢尔系统变化的风险.

最小的下注通常假定为等于1. 如果我们赢了, 我们的交易规模保持不变, 而我们的交易余额略有增加.

如果我们输了, 我们的下注大小增加1, 变成2, 而我们把输的注数加到一行记录上:

-1

如果这次我们赢了, 我们应该把2加到记录上:

-1 2

然后我们回顾这两个数字, 因为我们已经把输的赢回来了(换句话说, 我们已经通过两次下注又让我们的余额增加了1).

现在, 让我们考虑一个更长的失败序列.

-1

让我们下2注. 输了:

-1 -2

让我们下3注. 输了:

-1 -2 -3

让我们下4注. 输了:

-1 -2 -3 -4

让我们下5注. 输了:

-1 -2 -3 -4 -5

让我们下6注. 又输了:

-1 -2 -3 -4 -5 -6

让我们下7注. 我们终于赢了:

-1 -2 -3 -4 -5 -6 +7

这样, 我们去掉"-1", "-6"和"+7", 因为我们的赢盘抵消了两次失败的下注. 下面一次下注是记录中剩下的第一个和最后一个数值的和, 也就是, 仍然是7. 如果我们赢了:

-2 -3 -4 -5 +7
我们去掉 "-2", "-5" 和 "+7". 我们下一次的下注大小还是记录中剩下的第一个和最后一个之和. 是的, 仍然是7 (一些使用者推荐为下注再增加1, 这样如果我们走运就能够得到一个最小利润而不是0). 如果我们赢了: 
-3 -4 +7

我们把记录中全部数字去掉, 因为我们已经把我们输掉的赢回来了.

如果我们在中间阶段输掉了, 输掉的下注大小也被记录, 下一次下注还是等于记录中第一个和最后一个数值之和.

所以, 我们最初的结论是什么?

  1. 连续6次失败只需要3次获胜就能抵消掉(然而, 应该是连续获胜; 我们晚点再讨论). 乍一看来, 这个系统很容易让我们在市场上所向披靡.

  2. 下注大小的增长和马丁格尔相比明显变慢. 如果我们把这一序列用在马丁格尔系统中, 我们最后的那次下注, 大小是最初的64倍.

  3. 在上述例子中, 总的存款回撤(输掉的下注之和)只有21, 而使用马丁格尔的话, 就应该是63了.

  4. 通过简单计算显示, 如果每次下注使用1%的存款, 我们一连输掉13次才会输光我们的资金. 而如果每次用0.1%, 则需要连输44次. 你可能会想, "在50/50比例下连输44次!?这种可能性几乎没有!这就像被陨石砸到一样!这种可能性对我不错!", 等等.).

  5. 你可以很容易地找到许多关于马丁格尔系统回撤和危险的研究. 实际上, 你只要用纸和笔自己简单算算就能够知道回撤可能多厉害了. 但是, 我没有找到针对拉布谢尔系统的类似研究.

  6. 这个下注系统看起来非常复杂, 也就阻碍了其数学期望的计算.

但是让我们回头看看在下注中我们输掉的. 让我们假定, 我们连输了6次然后只是赢回两次而不是3次. 则我们的记录数据看起来如下:

-3 -4

我们下注7, 然后又输了:

-3 -4 -7
我们下注10(注意: 当我们输的时候, 下注的大小已经从3开始增长而不是1了, 这使我们的存款变得不那么安全了). 我们又输了: 
-3 -4 -7 -10

我们必须下注13了.

所以, 如果我们出现重复性的失败, 该系统会让我们的加注超过1. 这看起来是完全战胜回撤的唯一方法. 这就是我们的存款真正地陷入危机了, 因为我们需要一系列胜利来抵消回撤. 在纸上计算还是看起来太复杂了或者至少太麻烦了...

你是否还对这个系统能做什么感兴趣?如果是的话, 让我们再详细研究.


设定任务: 主题与方法

最重要的问题就是, 拉布谢尔资金管理系统是否真的能够把一个数学期望转化为真正的盈利方法. 当然, 引用的段落中提到的大约 33% 的胜率就输赢临界点听起来有些不可思议. 但是, 也许49% 或者 50% 的胜率就足够了?如果不是的话, 拉布谢尔系统有哪些其他优势呢?

我们将会使用统计学, 也就是说我们需要开发一个MQL程序(本例中是MQL4, 我还没有完全掌握MQL5). 让我们的程序来进行数以百万计的交易, 并且"清空"成千上万的存款 - 我们将会在不损坏我们真正资金的情况下分析结果. 如果程序可以盈利, 将有可能在真实交易中实现这算法.

拉布谢尔系统的开发是基于输赢比率相同的假定的. 其他比率情况下也可以采用此系统, 但是这看起来不大合理. 如果此系统可以影响输赢比率相同的数学期望, 它也应该影响其他的比率. 如果不能的话, 我们只是简单地浪费时间思考了一个合适的适应方案.

另外, 我们可以把输赢相同的系统想像成50%赢率的系统, 这样考虑就简单多了, 因为我们对抛硬币非常熟悉. 因此, 让我们把我们的程序叫做硬币测试(CoinTest).

首先, 我们应该描述我们未来程序的主要特性:

  1. 我们应该能够改变获胜可能性. 50/50比率只是一个特殊的平衡条件.

  2. 我们应该能够设置风险水平. 拉布谢尔系统有一个固定下注大小. 如果我们根据我们的存款规模来扩大初始赌注, 我们的存款将永远不会回到最初的状态, 因为所有的数值都比最初有所改变. 在有回撤退出后, 我们可以重新计算下注大小, 但是, 这将会引出难以处理的分数. 所以, 我们使用两个变量来设置风险 - 初始存款和初始下注.

  3. 有必要设置每笔存款的最大交易次数. 它应该被设置得足够大, 这样我们就能知道, 就算初始风险非常低的时候我们是否会损失全部存款. 毕竟, 如果存款持续增长, 这个过程可能是无限的, 我们可能永远都不知道结果.

  4. 我们应该有能力检查一个单一的存款的交易序列的结果, 这既是为了程序的调试, 也是为了我们可以改变交易逻辑. 把结果输出到文件中可以很好满足我们的目标.

  5. 在我们完成任务, 为单一存款过程写完代码后, 我们因该继续收集一系列独立的存款中(最好)使用不同参数过程的统计数据. 你要知道, 单一的试验几乎是没有意义的. 统计结果也被发送到文件中. 我们不需要每一个单独存款的历史.

我们的下注规模选择系统可能可以用于真实交易, 所以我们应该把它做成一个类.

对我们来说, 现阶段在MetaTrader中真的做交易没有必要, 因为会耗用很多计算资源. 我们只需要使用所需的规模和一个给定的胜率来得到随机交易的结果. 使用这种想法, 我们将会开发一个脚本程序, 因为这种MQL程序和EA交易或指标相比非常适合单独运行一次.


伪随机数生成器质量的统计学验证

伪随机数生成器(PRNG)的质量对我们非常重要, 因为它将用于定义每个交易的结果(赢/输). 一个很长的赢/输序列分布的准确性是最重要的. 晚些时候我们会尝试不使用复杂的数学和统计学理论对它进行评估.

这篇文章的目的不是对PRNG的质量做详细的研究(否则, 我们必须进行15个不同的测试). 我们所感兴趣的PRNG特点是它不会影响拉布谢尔系统的测试结果, 并不需要复杂的验证过程.

MetaTrader 有标准的 MathRand() PRNG 函数. PRNG 序列使用MathSrand() 函数进行初始化.

让我们写一个小的脚本程序 (RandFile) 来检查标准 PRNG 的质量. 此脚本程序将有两个参数:

  • 它应该可以生成数以百万计的32位随机数(每个32位随机数通过3次调用MathRand()函数, 每个函数可以提供15位). 测量单位通常是10进制的二不是2到2的20次方, 因为我们需要看到测试的结果.

  • CalcSeries 逻辑参数(是否应该计算相同位序列长度的分布).

对位序列长度分布的计算是非常耗费资源的(增加脚本执行时间十倍). 因而, 它被设为一个独立的选项.

该脚本程序生成如下结果:

  • 计算时间 (显示于日志中);
  • 全部生成位中1 位 的数量 (显示于日志中);
  • RandFile.bin 文件 — PRNG 运行结果的二进制文件;
  • RandStat.csv 文件 — 包含某些字节出现频率的记录文件;
  • RandOnesSeries.csv 文件 — 包含"1"位序列长度的记录文件;
  • RandZerosSeries.csv 文件 — 包含"0"位序列长度的记录文件.
让我们生成3个不同长度的测试集:
  • 1000万个测试数, 每个数字4个字节(一共4000万字节);
  • 1亿个测试数, 每个数字4个字节(一共4亿个字节);
  • 10亿个测试数, 每个数字4字节(一共40亿个字节).

现在让我们检查以下参数:

  1. 使用WinRAR最大压缩设置进行压缩, 包含随机数文件的压缩率. 高质量的随机数据是很难压缩的. 当然, 文件不能压缩的程度也不一定表示它们包含随机数的质量高. 但是如果它们很容易压缩, 这表明数据具有统计上的相似性.

    PRNG 生成1000万数字的压缩率

    PRNG 生成1亿数字的压缩率

    PRNG 生成10亿数字的压缩率

  2. "1" 位的数量:
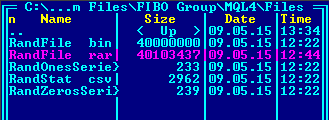
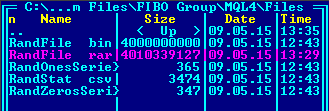
      平衡值 真实 绝对偏差
    		  偏差百分率
    10М
    		 160 000 000
    		 160 004 431
    		 4 431
    		 0,0027694
    100М
    		 1 600 000 000
    		 1 599 978 338
    		 21 662
    		 0,0013539
    1000М
    		 16 000 000 000
    		 15 999 996 180
    		 3 820
    		 0,0000239
  3. 某些字节的数值在随机数文件中出现的频率:

    PRNG 生成的某些字节出现频率, 1000万数字

    PRNG 生成的某些字节出现频率, 1亿数字

    PRNG 生成的某些字节出现频率, 10亿数字

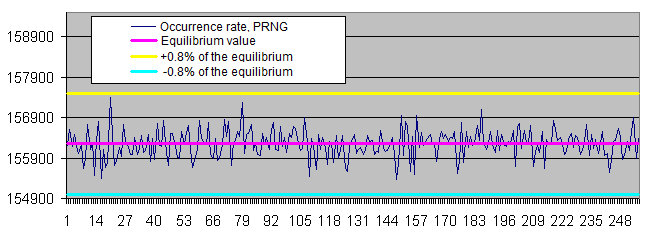
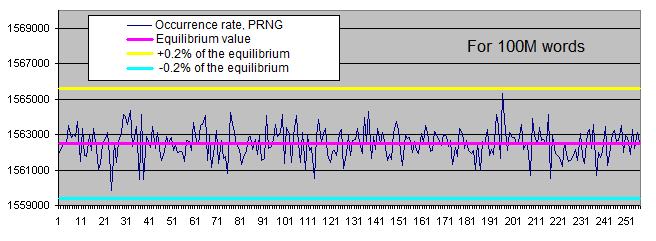
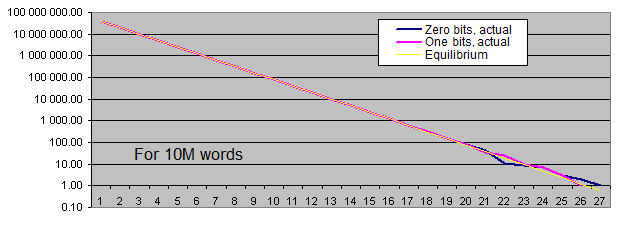
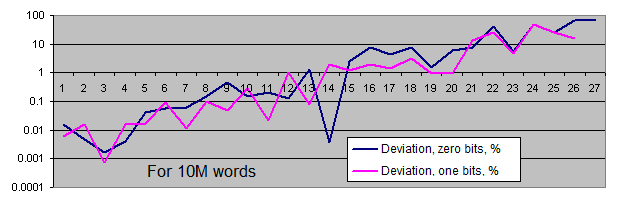
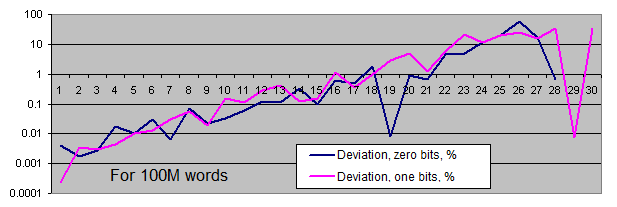
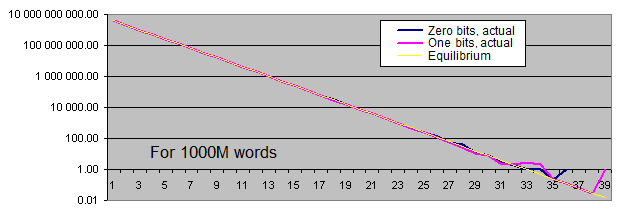
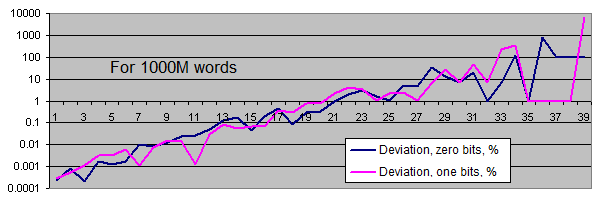
  4. 相同位序列的长度. 我们将对每个大小的样本生成两个图表:

    • 第一个显示某确定长度相同位的实际数量, 以及该系列的长度（在对数刻度）的平衡值;
    • 第二个显示实际量的百分比偏离检测到的相同的位序列(在对数刻度)的平衡值.

    线性图表是不符合我们要求的, 因为我们拥有的数据非常分散(在同一图表上, 数值从1到4,000,000,000或者从0.00001到6000)另外, 对数标度的长系列的平衡值的图表显示为直线, 而序列长度增加1，其发生的概率减少了一半。

1000万数字中, 相同位序列的长度

1000万数字中, 序列长度与平衡值的偏差

1亿数字中, 相同位序列的长度

1亿数字中, 序列长度与平衡值的偏差

10亿数字中, 相同位序列的长度

10亿数字中, 序列长度与平衡值的偏差

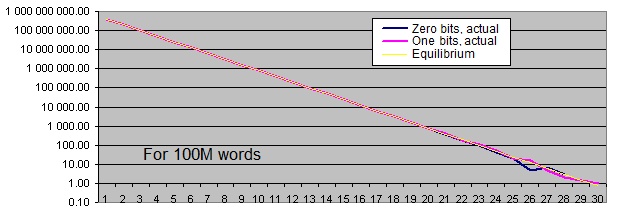
所以, 结论是什么呢?

  • 标准PRNG的效率对我们的任务来说是可以接受的.

  • 把包含PRNG运行结果的文件进行归档, 并不能压缩它们.

  • 位数中0和1的数量基本相同. 当样本规模增长时, 距离平衡点的偏差(百分率)会下降.

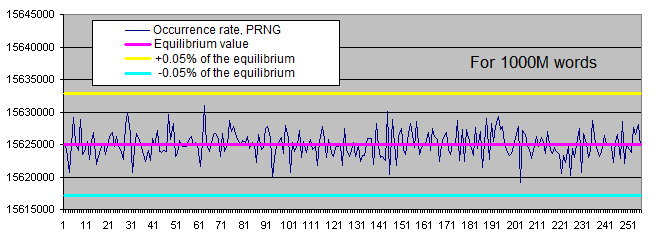
  • PRNG 运行中某些字节出现频率的分布只在平衡点附近小范围之内波动. 当样本规模增加时, 出现频率的离散程度会减小.

  • 只有在序列相当长的时候(非常罕见), 相同位的出现频率才会偏离平衡值. 当样本长度增加时, 实际发生率的"偏差点"移动才会远离平衡对增加的序列长度, 并始终位于周围的值的100个夹杂物的整个序列.

这样, 我们在标准PRNG中没有发现大的统计学缺陷, 即使一连生成30亿次(每个32位数字要生成3次), 我们的测试结果也没有问题.


写 CLabouchere 类的代码用于管理仓位大小

CLabouchere 类已经写得足够小了. 它的接口只包含两个封装函数, 用于设置/接收初始手数, 以及两个真正工作的函数 - 用于设置交易结果和获得当前仓位大小, 以及重设到初始状态:

// 拉布谢尔资金管理.
// 获利/止损假定为 1/1.
class CLabouchere
{
        private:
        protected:
                // 初始手数. 默认 - 0.1.
                double p_dStartLot;

                // 根据拉布谢尔系统原则, 包含手数数字的数组
                double p_dLotsString[];
        public:
                void CLabouchere();
                void ~CLabouchere();

                double GetStartLot() {return p_dStartLot;};
                void SetStartLot(double a_dStartLot) {p_dStartLot = a_dStartLot;};

                // 返回下一次进入市场的手数
                double GetCurrentLot();

                // 记下当前交易结果 - 赢 (true) 或输 (false)
                void SetResult(bool a_bResult);

                // 回到初始状态, 除了初始手数
                void Init() {ArrayResize(p_dLotsString, 0);};
};


写脚本程序. 初步评估

现在, 是时候写一个简单的差不多100个字的脚本程序了. 输入参数如下:

//--- 输入参数
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input double SuccessPercent = 50.0;
// 如果为 true, SuccessPercent 被忽略
input bool FiftyFifty = true;

该脚本会进行一系列交易, 直到存款输光或者交易数量达到了RepeatsCount.

此例中赢/输比例 = 50/50, 它是一个独立参数. 在后面的例子中, 使用了伪随机数的一位作为掷硬币的结果. 否则, 计算一个利润/损失边界值后, 用一个随机数与之作比较. 针对50/50例子的参数已经单独实现好了, 因为使用PRNG进行一位的循环很符合我们的需要, 尽管我们还没有评估这个循环出现值是否会超出边界值.

默认设置:

  • 存款规模 – 10 000;
  • 初始下注 – 50 (初始存款的0.5%).

大约在第十次运行脚本的时候, 我们收到了一个惊人的结果 - 存款在第2335步达到了46 300 . 然而, 在第2372步已经出现了回撤:

存款的增加和损失

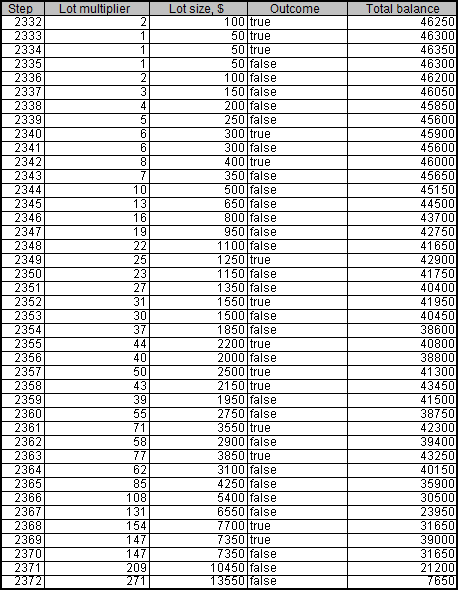
这就是图表上看起来的样子:

存款图表

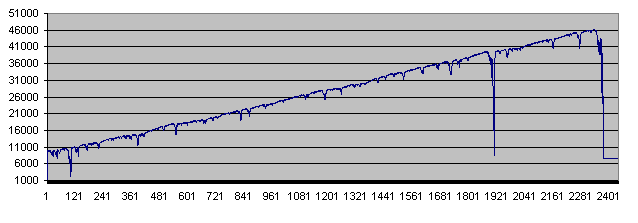
我们可以看到, 存款余额在最后被清零之前曾经有两次下跌得很严重.

有些情况下, 存款只在最初的几十次交易后就输光了, 甚至没有一个例子显示帐户达到了生命期的最大值, 100000次交易.

在我尝试各种不同参数时, 我想到了如下修改方式:

  • 这样做将是合理的: 增加一个参数来定义交易账户中资金回撤的数量. 如果我们可以在初始存款输光之前取回更多的资金, 我们的初始存款就可以被看成是可预见的损失. 就这样, 实现了新的叫做PocketPercent的参数. 它定义了在成功的交易之后我们从账户中取回资金并把它们放到"口袋"中. 不允许使用"口袋"中的钱, 只有交易账户中的钱可以用于风险的交易. 毕竟, 这和我们实际生活中发生的一样.

  • 当然, 存款过程应该是在一个循环中运行多次(如果我们人工运行数百次的话就太繁琐了). 我们应该修改一些参数 – PocketPercent 和 Take (初始下注大小), 以及计算平均结果 ("口袋"中的资金和账户中的存款, 因为账户存款永远不会下降到0, 它只会降低到无法进行下一次交易的程度).

  • 我们应该有了两个版本的脚本程序: 第一个循环重复运行而不把交易的详细信息记录到文件中, 而第二个则相反. 循环运行表示我们应该使用面向对象的代码. 因而, 我们把"运行代码"开发为CCoinTest 类, 而脚本程序代码则制作得尽可能简单.

运行一次的代码很短, 我可以把它在这里全部显示出来 (所有的工作, 包括把交易详情记入文件, 也是在CCoinTest类中完成的):

#include <CCoinTest.mqh>

//--- 输入参数
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input int PocketPercent = 10;
input double SuccessPercent = 50.0;
input string S2 = "如果为true, SuccessPercent 被忽略";
input bool FiftyFifty = true;
input string S3 = "如果为 true, 使用固定手数而不是拉布谢尔";
input bool FixedLot = false;

void OnStart()
{
        MathSrand(GetTickCount());

        CCoinTest Coin;

        Coin.SetRepeatsCount(RepeatsCount);
        Coin.SetStartBalance(StartBalance);
        Coin.SetTake(Take);
        Coin.SetPocketPercent(PocketPercent);
        Coin.SetSuccessPercent(SuccessPercent);
        Coin.SetFiftyFifty(FiftyFifty);
        Coin.SetFileName("Coin.csv");
        Coin.SetFixedLot(FixedLot);

        Coin.Go();
}

在我们增加了"口袋"之后, 系统的运行图表看起来有些不同了(在下面的例子中我们取回了 40% 的利润):

增加了"口袋"之后的余额图表(实例 1)

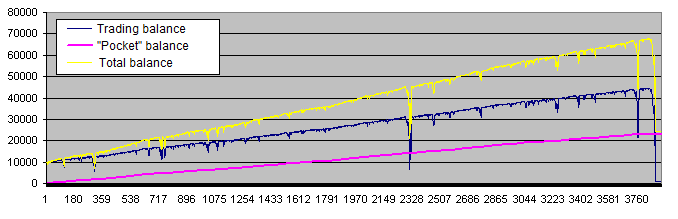
紫色线("口袋"余额)和每个交易者梦想的理想交易非常相近. 但是事实上, 我们应该更关注黄色线(交易账户与"口袋"的总额), 它看起来不大好. 另外, 以下图表更为常见:

增加了"口袋"的余额图表(实例 2)

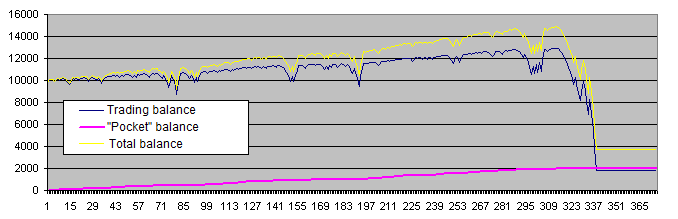
以下是我们现阶段的结论:

  • 此系统真正演示了作者期望的表现: 回撤经常被抵消, 而存款倾向于进一步增长.

  • 有些时候, 这样的尝试会以完全失败结束. 实际上, 系统在陷入回撤后只有两个选择 - 可能会战胜回撤, 或者把老本赔光.

  • 存款的生命越长, 增长的高度就越高.

  • 这些例子中的初始下注是存款初值的0.5%(10000中下注50). 在第一个例子中, 基本风险水平减少到0.1% (存款增长了4.5倍, 初始下注相同). 然而, 这些考量都没能保住存款, 还是输光了.


不同可能性的最终评估. 拉布谢尔系统与固定下注系统的比较结果

现在, 让我们转移到最激动人心的部分 - 把多个实验结果收集起来. 我们将会发现, 赢下的部分是否能盖过输掉的部分. 也许算法可以证实, 初始下注量是降低一些(这样可以为存款提供更多保护)还是提高一些才更加有效?我们从交易账户取出利润的百分比应该是多少呢?拉布谢尔系统和固定下注系统会有什么显著不同吗?如果初始系统有积极的数学期望("抛硬币"赢得多一些), 会发生什么呢?你看, 我们有很多不清楚的问题.

使用不同参数循环处理存款的脚本程序大约有100字. 我只展示其中的一部分.

输入参数:

//--- 输入参数
input int RepeatsCount=100000;
input int StartBalance = 10000;
input string S1 = "亏损资金";
input int Deposits = 100;
input double SuccessPercent = 50.0;
input string S2 = "如果为true, SuccessPercent 被忽略";
input bool FiftyFifty = true;
input string S3 = "如果为 true, 使用固定手数而不是拉布谢尔";
input bool FixedLot = false;

数组内包含着初始下注值和获胜后放到"口袋"中的百分数:

// 放到口袋百分比 数组
int iPocketPercents[24] = {1, 2, 3, 5, 7, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 75, 80, 85, 90, 95, 97, 98, 99};

// 初始下注数组
int iTakes[15] = {5, 10, 15, 20, 50, 75, 100, 150, 200, 300, 400, 500, 1000, 2000, 3000};

你可以看到, 初始下注量的范围是5 (初始存款的0.05%) 到 3 000 (初始存款的30%). 放到"口袋"中的资金百分比是从1%到99%. 这些参数在两个方向上都覆盖并超出了其合理的范围.

就这样, 搜索的空间也是双向的. 在此空间内选了360 (24 * 15) 个分离点. 基于序列的结果, 每个点都计算了平均总余额 ("口袋"资金 + 交易账户资金) 和账户亏光(存款生命期)前的交易量. 每个序列的存款数都记录在Deposits参数中.

此二维空间计算的结果是三维的, 也就是说很难使用二维方式显示它们. 为了解决这个问题, 我们在画二维图表的时候会使用x轴作为搜索空间内点的序列号(从0到359). 如果有必要, 某些 Takes 和 PocketPercent的值会独立提供.

在运行了100种存款数额之后, 平均余额如下:

100次迭代后的余额, 拉布谢尔系统, 50/50

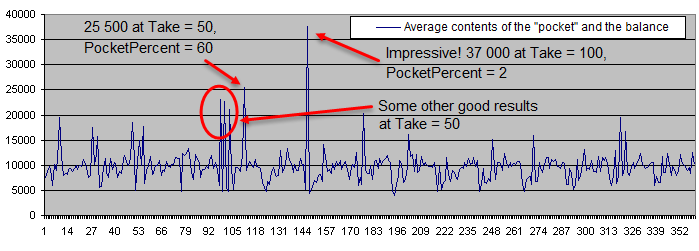
以下为存款生命期图表 (使用对数刻度):

存款生命期, 100次迭代, 拉布谢尔系统, 50/50

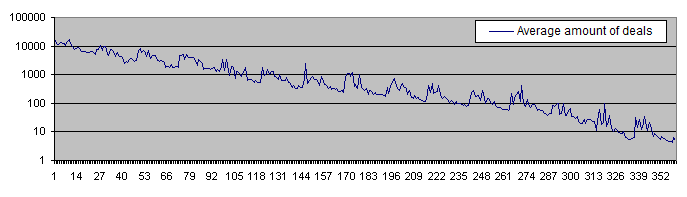
当初始风险为0.05%时, 存款生命期超过10000次交易, 而当初始风险为30%时, 存款生命期稳定下降到低于10次交易. 而高PocketPercent值也同样减少了亏光存款的平均交易次数. 这正是期待的结果.

我们可以在图表上选择几个点, 它们显示了"口袋"和余额的平均内容. 有四个点之间的距离非常接近, 所以希望我们能够找到最佳范围. 现在让我们计算Deposits = 1 000的结果, 并且把它们附加到同一图表上:

100次和1000次迭代后的余额, 拉布谢尔系统, 50/50

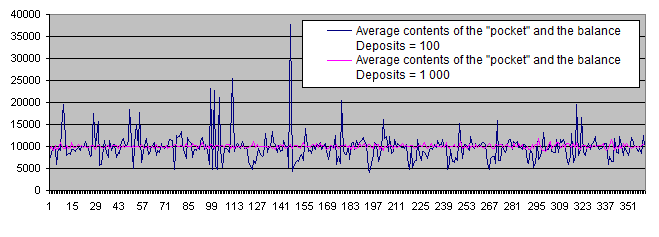
我们可以看到, 在足够大的统计数据的压力下, 想象中的最优区域也消失了. 不论使用什么参数, 图表只是在最初的余额10000附近随机波动.

因此, Deposits = 100 是不够的. 更多的试验将会使用Deposits = 1 000来做.

让我们在一张图表上显示拉布谢尔系统和固定下注系统的结果:

1000次迭代后的余额, 拉布谢尔系统和固定下注系统, 50/50

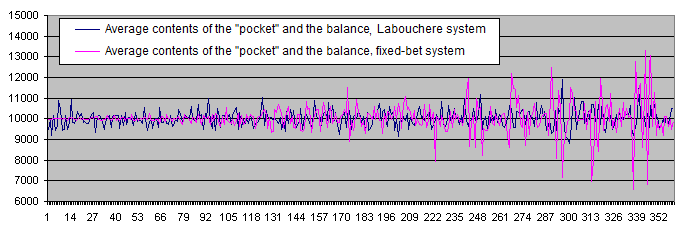
拉布谢尔系统和固定下注系同的存款生命期图表:

存款生命期, 1000次迭代, 拉布谢尔系统和固定下注系统, 50/50

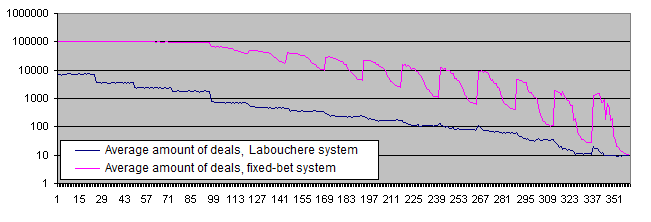
结论:

  • 拉布谢尔系统和固定下注系统的财务结果完全不一样.

  • 和拉布谢尔系统不一样, 固定下注系统显示的增长数据散布在平均值附近. 看起来固定的存款数和固定下注系统的统计行为不大相符.

  • 使用拉布谢尔系统的存款的生命期明显更短(大多数参数要低10多倍, 某些参数相差甚至超过100倍). 如果使用低风险水平, 我们可以看到图表达到了极限, 它是使用RepeatsCount 参数设置的 (默认值为 100 000). 这些结果部分确认了常见的观点, 即增加风险水平对存款来说是危险的. 这样的系统减少了存款的生命期, 尽管我们还没有发现存款上的风险 (至少平均来看有一部分盈利被取回了).

让我们引入一个新的脚本程序参数, 它使我们收集高风险区域的数据:

input string S2 = "每对参数的最小交易数.";
input int MinDeals = 10000000;

如果我们每1000次亏光存款而交易数少于1千万次, 我们应该继续.

结果, 图表数据变得不那么分散了:

余额, 在1000次迭代后, 并至少1千万次交易, 拉布谢尔系统和固定手数系统, 50/50

存款生命期, 1000次迭代并至少1千万次交易, 拉布谢尔系统和固定手数系统, 50/50

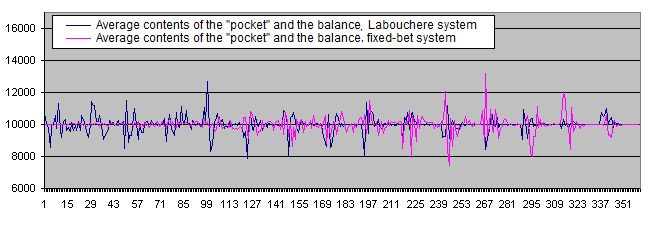
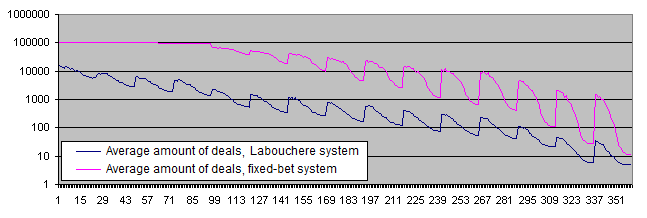
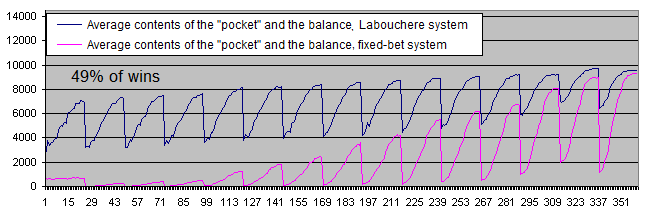
现在, 让我们使用初始系统胜率不等于50/50的参数检查系统的运行.

在1000次迭代后的余额, 拉布谢尔系统和固定手数系统, 49% 胜率

存款生命期:

存款生命期, 1000 次迭代, 拉布谢尔系统和固定手数系统, 49% 胜率

我们在这些图表上能看到什么呢?

  • 如果系统胜率是49%, 两个系统都明显不能盈利了.

  • 固定下注系统的财务结果明显较差, 这说明在胜率低于50%的情况下, 取出利润放到"口袋"的策略更加适用于拉布谢尔系统.. 只有在退出回撤的情况下, 资金才会被转移到"口袋"中.

    和固定下注系统不同, 即使是胜率为49%, 拉布谢尔系统能够不断刷新记录(只要前还够做另一次交易). 如果它们的存款快速减少, 直到输光之前, 人类交易者不大可能进行10万次或者甚至1万次交易. 他们肯定会早些停止交易. 而固定下注系统算法不能做到这一点. 在这个方面看, 拉布谢尔系统算法和人类更加接近. 因为它的行为更像一个人被新纪录所鼓舞, 然后不断交易直到暴仓.

你还记得我在简介部分提到的那篇诱导性的文章吗?它说的是系统即使在"33-40%"的胜率也可以工作. 让我们检查次范围的上限(40%):

1000 迭代后的余额, 拉布谢尔系统和固定手数系统, 40% 胜率

存款生命期, 1000次迭代, 拉布谢尔系统和固定手数系统, 40%胜率

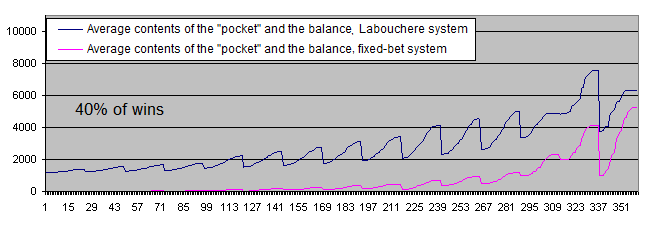
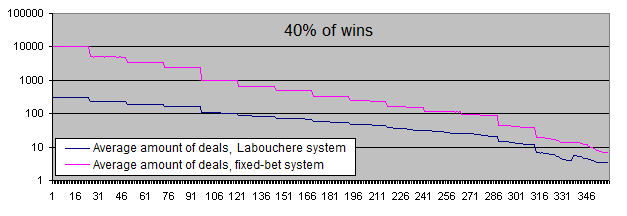
现在, 让我们考虑初始系统的数学期望为正的情况(胜率超过50%).

我们必须在对数刻度上显示余额图表, 甚至胜率只是51%.

1000次迭代后的余额, 拉布谢尔系统和固定手数系统, 51%胜率

存款生命期, 1000次迭代, 拉布谢尔系统和固定手数系统, 51%胜率

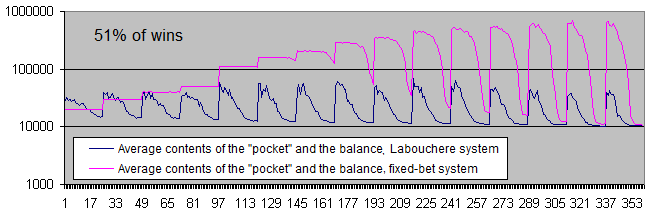
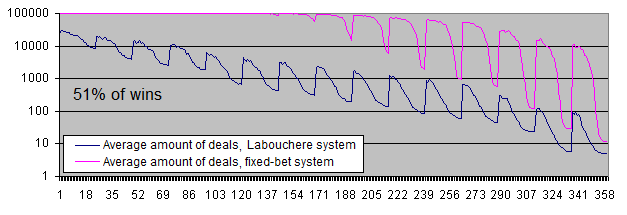
结论:

  • 两个系统都变得可以盈利了.

  • 如果风险水平低, 固定手数系统显示出无尽的"生命力". 换句话说, 几乎不可能输钱.

  • 然而, 拉布谢尔系统还是可能会暴仓 (但是别忘了我们还有"口袋").

  • 在大多数参数的情况下, 固定手数系统都会创造比拉布谢尔系统多十倍以上的利润(有些时候使用某些参数甚至达到了17倍).

大多数读者可能会想, 固定下注系统是全面超过拉布谢尔系统的. 不光它能更好地保护存款, 也能够创造10倍以上的利润!不幸的是, 他们被统计学给骗了.

固定手数系统碰巧有每份存款10万次交易的限制. 如果 RepeatsCount 参数设为200000, 系统就会创造2倍以上的利润. "但是这很好啊!" – 被统计学欺骗的读者会说. 他们又错了.

看一下每个系统(在对数刻度上)每次交易的平均利润:

每次交易利润, 拉布谢尔系统和固定手数系统, 51% 胜率

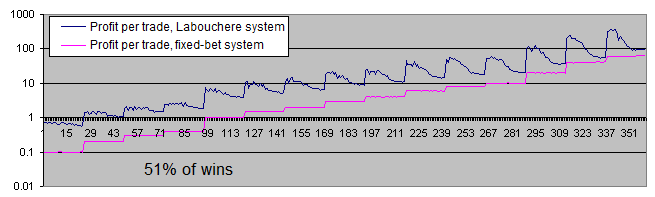
每次交易利润与初始下注的百分比图表使整个状况更加清晰:

每次交易利润与初始下注百分比, 拉布谢尔系统和固定手数系统, 51% 胜率

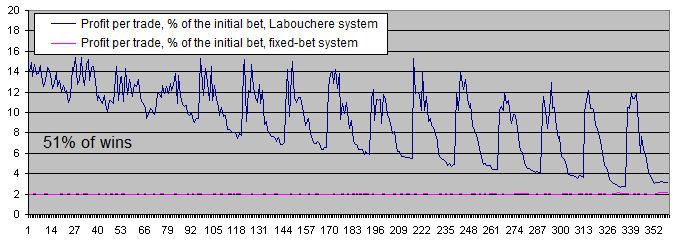
结论:

  • 固定下注系统每次交易的利润是初始下注的2%. 这和理论相符, 因为赢/输比率是51/49. 换句话说, 赢比输多2.

  • 拉布谢尔系统即使使用最不好的参数也能获得更多的利润. 如果参数设置得好, 它可能获得6到7倍以上的利润.

所以看起来, 如果你有无限的时间, 不使用拉布谢尔系统, 你可以做得很好.

你也许可以争辩, 固定下注系统可以用固定风险百分数系统来替代, 这样每次交易的利润就会增加(事实上, 利润会持续增长, 但是我们应该使用相同的距离来比较). 但是, 如果使用拉布谢尔系统作同样的改变, 结果也是这样.

所以, 拉布谢尔系统看起来更能盈利, 是吗?

如果您说是, 统计学又一次欺骗了您.

看一下表格:

 下注
大小		 百分比
转移到
"口袋"
 "口袋" 和余额
平均内容,
拉布谢尔系统		 平均
交易数量,
拉布谢尔系统
 "口袋" 和余额
平均内容,
固定下注
系统
  平均
交易数量,
固定下注
系统
 利润
每次交易,
拉布谢尔系统
利润
每次交易,
固定下注
系统

 利润
每次交易,
初始下注百分比,
拉布谢尔系统
 利润
每次交易,
初始下注
百分比, 固定下注
系统
75
 10
 51 177.34
 3 728.62
 160 489.6
 99 530.41
 11.04
 1.51
 14.72
 2.02
500
 45
 14 016.36
 127.27
 349 479
 33 771.46
 31.56
 10.05
 6.31
 2.01

实际上, 我们使用固定下注系统也可以轻易取得同样的利润. 我们只是需要简单地7次提高下注 (在本例中从0.75% 到 5% ). 当然, 5% 是一个非常高风险的水平. 但是在本例中固定下注系统还是更"坚强"10倍.

所以, 看起来固定下注系统更加有利, 是吗?

我想, 统计学再次背叛了你.

事实上, 不论您的存款可以在生存多少次交易 (当然是平均值), 因为我们已经把部分利润放到"口袋"中了. 如果"口袋"中的总资金超过了起初的账户余额数倍, 存款赔光并不是个大问题.

也许, 从这些计算中得出的最有用的结论应该如下: "如果胜率是51%, 拉布谢尔系统和固定下注系统的利润基本上是一样的, 前者的初始下注是存款的0.75%而从账户的最大回撤是10%, 而后者使用固定下注为初始存款的5%, 回撤为账户资金的45%. 拉布谢尔系统通过在运行中增加仓位大小达到了相同的获利水平".

另外, 请记住任何统计学的结论都是建立在进行大量试验的基础上的. 一个单独的虚拟帐户可以被虚拟分为多笔存款. 损失了虚拟存款说明失去了交易账户的部分存款, 并且当风险级别达到某种程度时回到初始下注水平. 然而, 本文显示, 即使模拟了100次存款, 得到的结果数据还是很分散的. 如果我们把一个普通交易者的存款分成100分, 通常就没有办法进行交易了.

那个系统更好?这很难说. 选择是根据交易者喜好, 初始系统的数学期望在这里至关重要. 文章中的代码允许任何人在他们自己的交易系统中模拟拉布谢尔系统.

让我们查看一下 55% 胜率下两个系统的图表:

1000次迭代后的账户余额, 拉布谢尔系统和固定手数系统, 55% 胜率

存款生命期, 1000 次迭代, 拉布谢尔系统和固定手数系统, 55% 胜率

每次交易利润, 拉布谢尔系统和固定手数系统, 55% 胜率

每次交易利润, 初始下注百分率, 拉布谢尔系统和固定手数系统, 55% 胜率

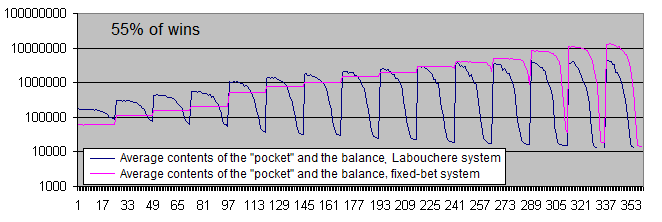
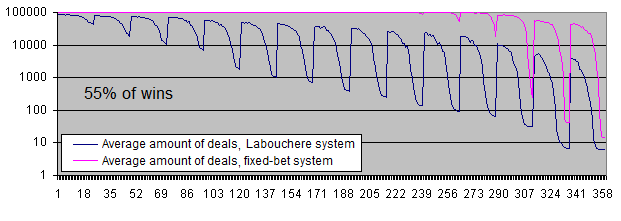
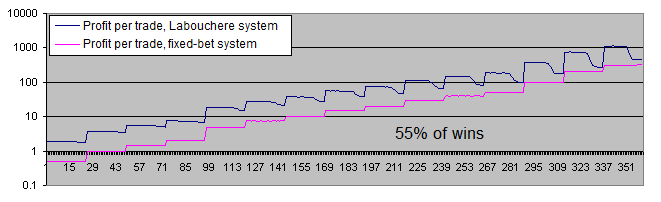
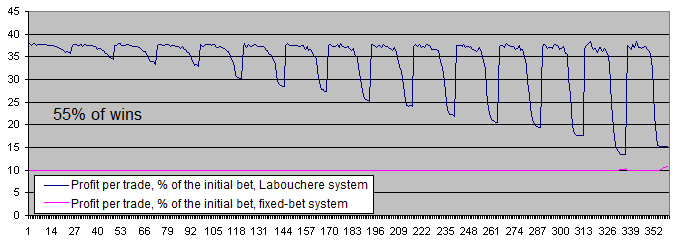
胜率为55%的话, 两个系统都可以盈利.

每次交易的平均利润已经从6到7倍(51%胜率)下降到3.7倍(55%胜率). 发生这种情况的原因是, 初始系统的胜率提高后, 拉布谢尔系统就会用更少的时间来恢复回撤, 所以就没有更加经常地增加手数进行交易.


结论

并没有奇迹发生. 拉布谢尔资金管理系统并不能把一个输钱甚至中性的系统变得获利.

另外, 拉布谢尔系统错觉的来源现在也显而易见了:

  • 复杂性阻碍了系统结果的计算.
  • 在人工测试中缺乏统计学数据.
  • 就算初始系统的期望为负面, 系统也可能不断创造出新的高利润记录, 然后使得交易者相信它的高效.

拉布谢尔系统是否值得使用正面期望的系统来尝试一下呢?选择是您自己的. 拉布谢尔系统非常复杂, 而它的效率很难说是突出的. 尽管这样, 我可以给您两点建议 - 如果您在意您的存款安全, 就不要使用超过可接受的风险级别, 另外尽量提高您交易系统的数学期望.

       

全部回复

0/140

量化课程

    移动端课程