目录
- 1. DBN 的结构
- 2. 数据的准备及选择
- 2.1. 输入变量
- 2.2. 输出变量
- 2.3. 初始化数据帧
- 2.3.1. 删除高相关性变量
- 2.4. 最重要变量的选择
- 3. 实验部分。
- 3.1. 构建模型
- 3.1.1. "darch" 软件包的简述
- 3.1.2. 构建 DBN 模型。参数。
- 3.2. 训练和测试样品的形成。
- 3.2.1. 分级平衡和预处理。
- 3.2.2. 目标变量编码
- 3.3. 训练模型
- 3.3.1. 预训练
- 3.3.2. 微调
- 3.4. 测试模型。标尺。
- 3.4.1. 预测解码。
- 3.4.2. 改善预测结果
- 校验
- 使用马尔科夫链模型进行平滑
- 在理论性平衡曲线上校正预测信号
- 3.4.3. 标尺
- 4. 智能交易程序的结构
- 4.1. 智能交易程序操作的描述
- 4.2. 自控制。自训练
- 安装和启动
- 改进定性指标的方式方法。
- 结论
概论
在准备进行实验的数据时, 我们将使用来自 前文 中有关评估和选择预测的变量。我们将形成初始样本, 清理它并选择重要的变量。
我们将研究为了训练、测试和验证而划分样本的方法。
我们将使用 "darch" 软件包构建一个 DBN 网络模型, 并用我们的数据对它进行训练。在模型之后测试, 我们将能获得评估模型质量的标尺。我们将研究软件包所提供的神经网络设置的多种配置机会。
另外, 我们会看到隐藏的马尔科夫模型将如何帮助我们改进神经网络预测。
我们将开发一款智能交易系统, 根据持续监测的结果, 在不打断交易的情况下对模型进行定期训练。在 EA 中将使用来自 "darch" 软件包的 DBN 模型。我们还将结合使用来自 前文 的 SAE DBN 构建智能交易系统。
再有, 我们将指点改进模型的定性指标的方式i和方法。
1. 由栈式 RBM (DN_SRBM) 初始化的深层神经网络的结构
我记得 DN_SRBM 是由 n 个等于神经网络隐藏层数的 RBM 组成, 基本上是神经网络本身。训练包括两个阶段。
第一阶段涉及预训练。每个 RBM 无需监督者即可依据输入集合系统地训练 (无目标)。在隐藏层的权重之后, RBM 被转移到相关的神经网络隐藏层。
第二阶段涉及微调, 在此神经网络由监督者训练。前文中已提供了有关它的详细信息, 所以我们在此不再复述。我将简单叙述, 不像我们前文用过的 "deepnet" 软件包, "darch" 软件包帮助我们实现更广泛的机会来构建并微调模型。更多详细信息将在创建模型时提供。图例. 1 显示 DN_SRBM 的结构和处理过程
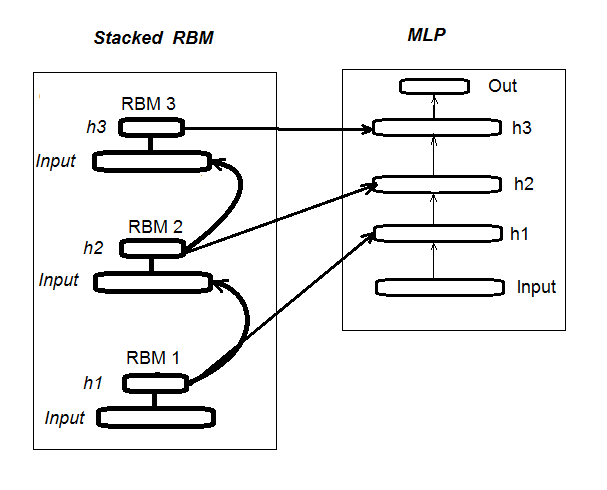
图例. 1. DN SRBM 的结构
2. 数据的准备及选择
2.1. 输入变量 (征兆, 预测器)
在前文中, 我们研究过预测器的评估和选择, 所以在此无需提供额外信息。我仅论及我们使用的 11 款指标 (所有的振荡器: ADX, aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, volatility)。选择了来自一些指标的若干变量。这样就形成了 17 个变量的输入集。我们从 EURUSD 里取最后 6000 根柱线的报价, 2016 年 02 月 14 日 M30 时间帧, 并使用 In() 函数计算指标值。
#---2--------------------------------------------- In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp - DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA") %>% as.data.frame() %>% mutate(., oscK = fastK - fastD) %>% transmute(.,slowD, oscK) %>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) kst <- KST(price[ ,4])%>% as.data.frame() %>% mutate(., oscKST = kst - signal) %>% select(.,oscKST) %>% as.matrix() In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, kst) return(In) }
我们将在输出上获得输入数据矩阵。
2.2输出数据 (目标白能量)
我们采用取自 ZZ 的信号作为目标变量。函数计算之字折线信号:
#----3------------------------------------------------ ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) require(magrittr) if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) if (mode == "m") {pr <- pr[ ,'Med']} if (mode == "hl") {pr <- pr[ ,c("High", "Low")]} if (mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) dz <- zz %>% diff %>% c(., NA) sig <- sign(dz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(cbind(zz, sig)) }
函数参数:
pr = 价格 – OHLCMed 报价的矩阵;
ch – 之字折线弯曲的最小长度点数 (4 位) 或是实际项 (例如, ch = 0.0035);
mode – 应用的价格 ("m" - 中间价, "hl" - 最高价和最低价, "cl" - 收盘价), 省缺使用中间价。
函数返回两个变量的矩阵 — 事实上, 之字折线和信号, 是在之字折线角度范围 [-1;1] 的基础上取得的。我们将信号向左平移一根柱线 (朝向未来)。这个特定的信号将用于训练神经网络。
我们计算信号时 ZZ 弯曲长度至少 37 点 (4 位)。
> out <- ZZ(ch = 37, mode = "m") Loading required package: TTR Loading required package: magrittr > table(out[ ,2]) -1 1 2828 3162
如我们所见, 分级略有失衡。当形成用于训练模型的样本时, 我们将采取必要的措施来令它们平衡。
2.3. 初始化数据帧
我们来编写创建初始数据帧的函数, 清理不确定的数据 (空) 并转换目标变量至两个分级的因子 "-1" 和 "+1"。函数组合之前编写的函数 In() 和 ZZ()。我们将立即裁剪最后 500 根柱线, 用于评估模型预测质量。
#-----4--------------------------------- form.data <- function(n = 16, z = 37, len = 500){ require(magrittr) x <- In(p = n) out <- ZZ(ch = z, mode = "m") data <- cbind(x, y = out[ ,2]) %>% as.data.frame %>% head(., (nrow(x)-len))%>% na.omit data$y <- as.factor(data$y) return(data) }
2.3.1. 删除高相关性变量
我们将从初始集合里面删除相关性系数高于 0.9 的变量。我们将编写形成初始数据帧的函数, 删除高相关性变量并返回清理后数据。
我们可以预先检查哪一个变量的相关性系数高于 0.9。
> data <- form.data(n = 16, z = 37) # 准备数据帧 > descCor <- cor(data[ ,-ncol(data)])# 删除目标变量 > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.1887 0.0532 0.2077 0.3040 0.5716 0.9588 > highCor <- caret::findCorrelation(descCor, cutoff = 0.9) > highCor [1] 12 9 15 > colnames(data[ ,highCor]) [1] "rsi" "cmo" "SMI"
因此, 以上列出的变量可以删除。我们将从数据帧里删除它们。
> data.f <- data[ ,-highCor] > colnames(data.f) [1] "DX" "ADX" "oscDX" "ar" "tr" [6] "atr" "cci" "chv" "sign" "vsig" [11] "slowD" "oscK" "signal" "vol" "Class"
我们可在一个函数里紧凑地编写它:
#---5----------------------------------------------- cleaning <- function(n = 16, z = 37, cut = 0.9){ data <- form.data(n, z) descCor <- cor(data[ ,-ncol(data)]) highCor <- caret::findCorrelation(descCor, cutoff = cut) data.f <- data[ ,-highCor] return(data.f) } > data.f <- cleaning()
并非所有软件包的作者和研究人员都同意将高相关性的数据从集合中删除。不过, 两种使用结果会在此进行比较。在我们的情况中, 我们选择的选项是删除。
2.4. 最重要变量的选择
重要变量的选择基于三个指标: 按照分级的全局重要性, 局部重要性 (结合) 和部分重要性。我们要把握前文详述的 "randomUniformForest" 软件包的机会。为了紧凑性, 所有之前和之后的动作均在一个函数收集。一旦执行, 我们将获取三个集合作为结果:
- 具有最佳贡献和交互的变量;
- 对于分级 "-1" 的最佳变量;
- 对于分级 "+1" 的最佳变量。
#-----6------------------------------------------------ prepareBest <- function(n, z, cut, method){ require(randomUniformForest) require(magrittr) data.f <<- cleaning(n = n, z = z, cut = cut) idx <- rminer::holdout(y = data.f$Class) prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method) x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)]) x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)]) y.train <- data.f[idx$tr, ncol(data.f)] y.test <- data.f[idx$ts, ncol(data.f)] #--------- ruf <- randomUniformForest( X = x.train, Y = y.train, xtest = x.test, ytest = y.test, mtry = 1, ntree = 300, threads = 2, nodesize = 1 ) imp.ruf <- importance(ruf, Xtest = x.test) best <- imp.ruf$localVariableImportance$classVariableImportance %>% head(., 10) %>% rownames() #-----部分重要 best.sell <- partialImportance(X = x.test, imp.ruf, whichClass = "-1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] best.buy <- partialImportance(X = x.test, imp.ruf, whichClass = "1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] dt <- list(best = best, buy = best.buy, sell = best.sell) return(dt) }
我们将声明函数计算的顺序。官方参数:
n – 输入数据参数;
z – 输出数据参数;
cut – 变量的相关性阀值;
method – 输入数据预处理方法。
计算顺序:
- 创建初始的 data.f 集合, 高相关性变量已移除, 并将之保存以备后用;
- 识别训练索引和 idx 的测试样本;
- 判断 prep 的预处理参数;
- 将初始样本划分为训练和测试样本, 输入数据规范化;
- 在所获取的集合之上获取并测试 ruf 模型;
- 计算 imp.ruf 变量的重要性;
- 选择 10 个贡献和交互度最重要的变量 — 最佳;
- 选择 7 个对于 "-1" 和 "+1" 分级最重要的变量 — 最佳买入, 最佳卖出;
- 创建三个预测器的集合列表 — 最佳, 最佳买入, 最佳卖出。
我们将计算这些样本, 并评估所选择变量在全局、局部和部分的重要性数值。
> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign")) 加载所需软件包: randomUniformForest 标签 -1 1 已被转换到 1 2 为了 便于计算并将在内部使用 作为 替换。 1 - 全局变量重要性 (14 基于所获信息最重要) : 注意: 大多的预测特征按照 'score' 排序并作图。大多数判别式 应考虑搜索 'class' 和 'class.frequency'。 变量得分 class class.frequency 百分比 1 cci 4406 -1 0.51 100.00 2 signal 4344 -1 0.51 98.59 3 ADX 4337 -1 0.51 98.43 4 sign 4327 -1 0.51 98.21 5 slowD 4326 -1 0.51 98.18 6 chv 4296 -1 0.52 97.51 7 oscK 4294 -1 0.52 97.46 8 vol 4282 -1 0.51 97.19 9 ar 4271 -1 0.52 96.95 10 atr 4237 -1 0.51 96.16 11 oscDX 4200 -1 0.52 95.34 12 DX 4174 -1 0.51 94.73 13 vsig 4170 -1 0.52 94.65 14 tr 4075 -1 0.50 92.49 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 7 14 7 2 - 局部变量重要性 变量交互 (10 在首行和第二列顺序的最重要变量) : 对于每个变量 (每个顺序), 它们彼此间的交互性 也 已计算。 cci slowD atr tr DX atr 0.1804 0.1546 0.1523 0.1147 0.1127 cci 0.1779 0.1521 0.1498 0.1122 0.1102 slowD 0.1633 0.1375 0.1352 0.0976 0.0956 DX 0.1578 0.1319 0.1297 0.0921 0.0901 vsig 0.1467 0.1209 0.1186 0.0810 0.0790 oscDX 0.1452 0.1194 0.1171 0.0795 0.0775 tr 0.1427 0.1168 0.1146 0.0770 0.0750 oscK 0.1381 0.1123 0.1101 0.0725 0.0705 sign 0.1361 0.1103 0.1081 0.0704 0.0685 signal 0.1326 0.1068 0.1045 0.0669 0.0650 avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775 vsig oscDX oscK signal ar atr 0.1111 0.1040 0.1015 0.0951 0.0897 cci 0.1085 0.1015 0.0990 0.0925 0.0872 slowD 0.0940 0.0869 0.0844 0.0780 0.0726 DX 0.0884 0.0814 0.0789 0.0724 0.0671 vsig 0.0774 0.0703 0.0678 0.0614 0.0560 oscDX 0.0759 0.0688 0.0663 0.0599 0.0545 tr 0.0733 0.0663 0.0638 0.0573 0.0520 oscK 0.0688 0.0618 0.0593 0.0528 0.0475 sign 0.0668 0.0598 0.0573 0.0508 0.0455 signal 0.0633 0.0563 0.0537 0.0473 0.0419 avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545 chv vol sign ADX avg2ndOrder atr 0.0850 0.0850 0.0847 0.0802 0.1108 cci 0.0824 0.0824 0.0822 0.0777 0.1083 slowD 0.0679 0.0679 0.0676 0.0631 0.0937 DX 0.0623 0.0623 0.0620 0.0576 0.0881 vsig 0.0513 0.0513 0.0510 0.0465 0.0771 oscDX 0.0497 0.0497 0.0495 0.0450 0.0756 tr 0.0472 0.0472 0.0470 0.0425 0.0731 oscK 0.0427 0.0427 0.0424 0.0379 0.0685 sign 0.0407 0.0407 0.0404 0.0359 0.0665 signal 0.0372 0.0372 0.0369 0.0324 0.0630 avg1rstOrder 0.0497 0.0497 0.0495 0.0450 0.0000 基于交互性的变量重要性 (10 最重要) : cci atr slowD DX tr vsig oscDX 0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 oscK signal sign 0.0599 0.0509 0.0464 覆盖标签的变量重要性 (10 对于每个标签最重要变量条件) : Class -1 Class 1 cci 0.17 0.23 slowD 0.20 0.09 atr 0.14 0.15 tr 0.04 0.12 oscK 0.08 0.03 vsig 0.06 0.08 oscDX 0.04 0.08 DX 0.07 0.08 signal 0.05 0.04 ar 0.04 0.02
结果
- 在全局重要性方面, 所有 14 个输入变量相等。
- 按照整体贡献 (全局重要性) 和交互性 (局部重要性) 定义的 10 个最佳。
- 每个分级的七个最佳部分重要性变量显示在以下图表。
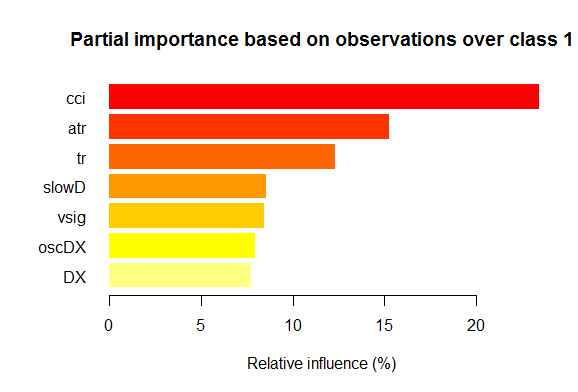
图例. 2. 对于分级 "1", 变量的部分重要性
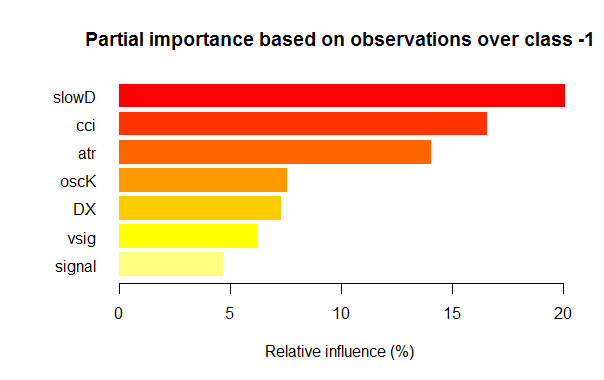
图例. 3. 对于分级 "-1", 变量的部分重要性
正如我们所看到的, 对于不同分级, 最重要的变量在结构和排名上均有差异。所以, 如果对于 "-1" 分级, slowD 变量是最重要的, 而对于 "+1" 分级它仅排位第 4。
因此, 我们的数据集合已就绪。现在我们可以进行实验。
3. 实验部分。
实验将指定以 R 语言进行 — 革命 R 开源, 版本 3.2.2, 由 Revolution Analytics 公司发行。http://www.revolutionanalytics.com/revolution-r-open
该发行版本在正规的 R 3.2.2 之上有编号 advantages :
- 通过应用 Intel® 数学内核库 的多线程处理, 进行快速且更定性的计算;
- 可重现 R 工具箱高级功能。一个小小的澄清: R 语言正在积极发展, 不断改进现有软件包, 并添加新功能。这种进展的反面则涉及到可重现的丧失。也就是说, 您几个月之前编写的产品运行良好, 但在下次软件包更新后突然停工。大量的时间会浪费在识别并清除由更新的软件包导致的错误。例如, 第一篇深度神经网络文章附加的智能交易系统在创建之时功能良好。然而, 发布几个月之后一些用户抱怨它已不可运行。分析表明是更新的 "svSocket" 软件包引起智能交易系统的故障, 而且我无法找到其背后的原因。最后版本的智能交易系统将附加在本文。这个问题已经成为一个迫切的问题, 在 Revolution Analytics 里它很容易解决。现在, 当新版本发行时, 所有在 CRAN 存储库中的软件包会在发布日期被固定, 并拷贝至它们的镜像。在此日期之后 CRAN 存储库中的任何变化都不会影响 Revolution 镜像上的 "冻结" 软件包。此外, 从 2014 年 10 月开始, 公司每天制作 CRAN 存储库的快照, 修复软件包相关的状态和版本。依照他们自己的 "检查点" 软件包, 我们现在可以下载所需日期的相关必要软件包。换言之, 我们是在操纵某种时间机器。
另一个新闻。九个月前, 当微软收购 Revolution Analytics 时, 它承诺支持他们的发展, 并保持革命 R 开源 (RRO) 的免费发行。随后是一些有关 RRO 和革命 R 企业版新颖特色的若干消息 (并非 R 语言与 SQL 服务器, PowerBI, Azure 和 Cortana Analitics 的集成)。现在我们得到情报, 下一个版本的 RRO 更新版将称为 Microsoft R Open, 而革命 R 企业版 — Microsoft R 服务器。不久以前, 微软已经宣布 R 语言将在 Visual Studio 中提供。R Tools for Visual Studio (RTVS) 随同 Python Tools for Visual Studio 模型。 它将被免费添加到 Visual Studio 中, 并为 R 语言提供一个完整的集成开发环境, 包括编辑和交互式调试脚本。
到本文完成时, Microsoft R Open (R 3.2.3) 已经发布, 因此, 在本文中, 我们将引用此版本的软件包。
3.1. 构建模型
3.1.1. "darch" 软件包的简述
"darch" 版本。0.10.0 软件包提供广泛的函数, 不仅可令我们创建和训练模型, 而且, 从字面上来理解, 它可根据您的喜好一砖一瓦地构建并调整。如前指出的, 深层神经网络由 n 个RBM (n =层-1) 和多层 MLP 神经网络组成。逐层 RBM 预训练在无格式数据基础上执行且无需监督者。神经网络的微调需依赖监督者和格式化数据才可执行。划分训练阶段为我们提供了使用各种体量数据的机会 (但不是结构!), 或者在单独预训练的基础上获得一些各种微调的模型。此外, 如果用于预训练和微调的数据相同, 则可以训练一次, 而不是分成两个阶段。或者, 您可以跳过预训练并只使用多层神经网络, 或在另一方面, 只使用 RBM, 而无需神经网络。同时我们可以访问所有内部参数。软件包适用于高级用户。更进一步, 我们将分析划分过程: 预训练和微调。
3.1.2. 构建 DBN 模型。参数。
我们将描述 DBN 模型建立、训练和测试的过程。
newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),
此处:
- layers: 数组指示层的数量和每一层神经元的数量。例如: layers = c(5,10,10,2) – 一个具有 5 个神经元的输入层 (可见), 两个每层具有 10 个神经元的隐藏层, 以及一个具有 2 个输出的输出层。
- BatchSize: 训练期间微型样本的尺寸。
- ff: 指示 ff 格式是否应用于权重、背离和退出。ff 格式用来压缩保存大体量数据。
- LogLevel: 执行此功能时日志和输出的级别。
- GenWeightFunction: 用于生成 RBM 权重矩阵的函数。这是一个使用用户激活功能的机会。
创建的 darch 对象包含 (layers - 1) RBM, 组合到累积的网络并将用于预训练神经网络。两个属性 fineTuneFunction 和 executeFunction 包括的函数用于微调 (backpropagation 省缺) 和用于执行 (runDarch 省缺)。神经网络的训练是通过两个训练函数来执行: preTrainDArch() 和 fineTuneDArch()。第一个函数使用对比背离的方法训练 RBM 网络且无需监督者。第二个函数使用在 fineTuneFunction 属性里指明的函数进行神经网络微调。在神经网络执行之后, 每层的输出可以在 executeOutputs 属性中找到, 或者 executeOutput 属性中仅有的输出层。
2. darch 对象预训练函数
preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),此处:
- darch: 'Darch' 类的实例;
- dataSet: 用于训练的数据;
- numEpoch: 训练周期的次数;
- numCD : 采样迭代次数。通常, 一就足够了;
- ... : 附加参数可传送到 trainRBM 函数;
- trainOutputLayer: 逻辑值显示是否 RBM 的输出层应该训练。
函数为每个 RBM 执行 trainRBM() 训练函数, 拷贝训练后的权重和背离至相关 darch 对象的神经网络层。
3. darch 对象的微调函数fineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T,
isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101,
stopValidErr = -Inf, stopValidClassErr = 101, ...),
此处:
- darch: 'Darch' 类的样本;
- dataSet: 训练数据集合 (可用于验证) 和测试;
- dataSetValid : 用于验证的数据集合;
- numxEpoch: 训练周期的次数;
- bootstrap: 逻辑, 当创建验证数据时是否需要应用自举;
- isBin: 指示输出数据是否应解释为逻辑值. 省缺 — FALSE。如果 TRUE, 每个高于 0.5 的值解释为 1, 而低于 — 则为 0。
- isClass : 指示是否针对分类训练网络。如果 TRUE, 则确定针对分类统计。TRUE 为省缺。
- stopErr : 由于训练期间发生的错误而导致神经网络停止训练的标准。-Inf 为省缺;
- stopClassErr : 由于训练期间发生的分类错误而导致神经网络停止训练的标准。101 为省缺;
- stopValidErr : criterion for stopping the neural network due to error in validation data. -Inf 为省缺;
- stopValidClassErr : 由于验证期间发生的分类错误而导致神经网络停止的标准。101 为省缺;
- ... : 可以传递到训练函数的参数。
函数训练网络是通过保存在 darch 对象 fineTuneFunction 属性中的函数。属于它们 (targetData, validTargets, testTargets) 的输入数据 (trainData, validData, testData) 和类可以作为 dataSet 或 ff-matrix 转移。用来验证和测试的数据和类不是强制性的。如果提供它们, 则将使用这些数据集合来执行神经网络, 并且计算统计。属性 isBin 指示是否输出数据应解释为二进制。如果 isBin = TRUE, 每个高于 0.5 的输出数据解释为 1, 否则 — 为 0。还有, 我们可以在训练或验证集合上设置一个基于错误 (stopErr, stopValidErr) 或正确分类 (stopClassErr, stopValidClassErr) 的训练停止标准。
所有函数参数都有默认值。当然, 也可以使用其它值。因此, 例如:
神经元激活函数 — sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative 是可用的。 sigmoidUnitDerivative 作为省缺。
神经网络的微调函数 — backpropagation 作为省缺, 弹性传播 rpropagation 也可用在四个变量 ("Rprop+", "Rprop-", "iRprop+", "iRprop-") 和 minimizeClassifier (此函数经 Darch 网络分类器使用非线性共轭梯度法训练) 中。对于后两个算法以及对主题有深入了解的人, 提供了神经网络进行多参数配置微调的单独实现。例如:
rpropagation(darch, trainData, targetData, method="iRprop+",
decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
minDelta=0.000001, maxDelta=50, ...),
此处:
- darch – 用于训练的 darch 对象;
- trainData – 用于训练的输入数据;
- targetData – 期望的用于训练的输出集合;
- method – 训练方法。"iRprop+" 为省缺。"Rprop+", "Rprop-", "iRprop-" 是可能的;
- decFact – 用于训练的递减因子。0.5 为省缺;
- incFact - 用于训练的递增因子。1.2 为省缺;
- weightDecay – 在训练时递减权重。0 为省缺;
- initDelta – 在更新时的初始值。0.0125 为省缺;
- minDelta – 步长尺寸的最小边界。0.000001 为省缺;
- maxDelta – 步长尺寸的最大边界。50 为省缺。
函数返回已训练的神经网络 darch 对象。
3.2. 训练和测试样品的形成。
我们已形成了初始数据样本。现在, 我们需要将其分为训练、验证和测试样本。省缺比率为 2/3。各种软件包均有许多用于分割样本的函数。我使用 rminer::holdout(), 它计算将初始样本分解为训练和测试的样本。
holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
seed = NULL, window=10, increment=1),
此处:
- y – 期望目标变量, 数字向量或因子, 在此情况下, 要进行分层拆分 (即, 分级间的比例对于所有部分均相同);
- ratio – 拆分比率 (百分比 — 训练样本的大小已建立; 或样本总数 — 测试样本大小已建立);
- internalsplit – 如果 TRUE, 则训练数据就要再次拆分为训练和验证样本。对于内部拆分应用相同的比率;
- mode – 采样模式。可用选项:
- stratified – 分层随机切分 (如果 у 因子; 否则标准随机切分);
- random – 标准随机切分;
- order – 静态模式, 当第一个例程用于训练时, 且其余的 — 用于测试 (广泛应用于时间序列);
- rolling – 滚动窗口, 通常称为滑动窗口 (广泛应用于股票和金融市场的预测), 类似于 order, 除了窗口指代窗口大小, iter — 滚动迭代和增量 — 每次迭代时窗口向前滑动的样本数量。窗口每次迭代时的训练样本大小是固定的, 而测试样本等于比率, 除了最后一次迭代 (这次可能较少)。
- incremental – 重新训练的增量模式, 也称为增增量窗口, 与 order 相同, 除了窗口是初始窗口大小, iter - 增量迭代和增量 - 每次迭代添加的样本数量。训练样本的大小在每次迭代时增长 (+增量), 而测试集合的大小等于比率, 除了最后一次迭代, 此处它可能较少。
- iter – 重新训练增量模式的迭代数量 (仅用在 mode = "rolling" 或 "incremental", iter 通常设为循环)。
- seed – 若是 NULL, 则使用随机种子, 否则种子为固定 (以后的计算一直返回相同结果);
- window – 训练窗口的大小 (若是 mode = "rolling") 或训练窗口初始尺寸 (若 mode = "incremental");
- increment – 每次迭代时训练窗口增加的样本数量 (若 mode="incremental" 或 mode="rolling")。
3.2.1. 分级平衡和预处理。
我们将编写一个函数, 此函数将样本中的分级数量向更高的数量对齐 (如果需要的话), 切分样本为训练和测试样本, 执行预处理 (若必要, 规范化), 并返回相对应样本的列表 — 训练, 测试。为了达成平衡, 我们将会使用 caret::upSample() 函数, 增加样本随机替换, 使得分级的分布相等。我必须说, 并不是所有的研究人员都发现有必要平衡分级。但是, 正如已知的, 实践是检验真理的标准, 并且我的多个实验结果表明, 样本平衡在训练中总是显示出更佳的结果。尽管, 这不会阻止我们进行自己的实验。
对于预处理我们将使用 caret::preProcess() 函数。预处理参数将保存在 prepr 变量。由于我们已在前文中研究并应用过它们, 因此我不会在这里进一步赘述。
prepareTrain <- function(x , y,
rati, mod = "stratified",
balance = F,
norm, meth)
{
require(magrittr)
require(dplyr)
t <- rminer::holdout(y = y, ratio = rati,
mode = mod)
train <- cbind(x[t$tr, ], y = y[t$tr])
if(balance){
train <- caret::upSample(x = train[ ,best],
y = train$y,
list = F)%>% tbl_df
train <- cbind(train[ ,best], select(train, y = Class))
}
test <- cbind(x[t$ts, ], y = y[t$ts])
if (norm) {
prepr <<- caret::preProcess(train[ ,best], method = meth)
train = predict(prepr, train[ ,best])%>% cbind(., y = train$y)
test = predict(prepr, test[ ,best] %>% cbind(., y = test$y))
}
DT <- list(train = train,
test = test)
return(DT)
}
有关预处理的一个注释: 输入变量将被规范化到范围 (-1, 1)。
3.2.2. 目标变量编码
当求解分类任务时, 目标变量是具有几个级别的因子。在模型中, 它被设置为由后续目标状态组成的向量 (列)。例如, y = с("1", "1", "2", "3", "1")。为了训练神经网络, 目标变量必须被编码 (变换) 为列数等于分级数的矩阵。矩阵的每一行中, 只有一列可以包含 1。这种变换在输出层伴同使用 softmax() 激活函数, 可以获得每级预测目标变量的状态概率。函数 classvec2classmat() 将用来编码。这不仅是为目标变量编码的最佳方法, 而且因其简单我们才会用它。目标变量预测值的逆变换 (解码) 是通过我们即将涵盖的不同方法来实现的。
3.3. 训练模型
3.3.1. 预训练
如上所述, 首先, 我们创建名为 DArch 的深层体系对象, 包括所需数量的具有省缺初始训练参数的 RBM, 以及省缺采用随机权重和神经元激活函数集合的初始化神经网络。在对象创建阶段, 如有必要, 可以改变预训练参数。之后, 通过发送训练样本 (没有目标变量) 到输出来预训练 RPM 网络且无需监督者。当其完成之后, 我们得到 DАrch, 此处将在 RBM 训练期间所获得的权重和背离传递到神经网络。我们应以向量的形式预先设置隐藏神经元在层中的分布 (例如):
L<- c( 14, 50, 50, 2)
输入层中的神经元数量等于输入变量的数量。两个隐藏层每层将包含 50 个神经元, 输出层将有两个。我来解释最后一点。如果目标变量 (因子) 具有两个级别, 则事实上一个输出就足够了。但是将向量转换为两列矩阵, 它们当中的每一个对应于一个分级, 可令我们应用 softmax激活函数, 它会在分类任务的输出层操作良好。再有, 分级概率形式的输出令我们在随后的结果分析中拥有额外的机会。本主题将很快涵盖。
当训练设为实验时周期数通常在 10-50 的范围内。
采样迭代次数将保持省缺状态, 但如果您想要进行实验, 可以增加此参数。它将在单独的函数中定义:
#----8-------------------------------------------------------------- pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9) { require(darch) # 创建 DArch dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5) # 设置初始量 setInitialMomentum(dbn) <- InM # 设置最终量 setFinalMomentum(dbn) <- FinM # 设置从初始到最终量的切换时间 setMomentumSwitch(dbn) <- round(0.8 * nE) dbn <- preTrainDArch(dbn, dataSet = dS, numEpoch = nE, numCD = nCD, trainOutputLayer = T) return(dbn) }
3.3.2. 微调
正如之前讨论的, 软件包提供 backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder() 用于微调。最后两个将不考虑, 因为它们在软件包里没有足够的文档, 且没有如何应用它们的例程。这些函数在我的实验中没有显示出良好的效果。
我也想添加一些关于软件包的更新。当我开始写这篇文章时, 当时的版本是 0.9, 可当我完成它时, 一个包含多个更新的 0.10 版本已发布。所有的计算必须重做。基于短期测试的结果, 我可以说操作速度增幅相当大, 不像结果的质量 (这更多是用户的错误, 然后是软件包)。
我们来研究前两个函数。第一个 (backpropagation) 在 DАrch 对象里设为省缺, 所使用的训练神经网络参数在此提供。第二个函数 (rpropagation) 也有省缺参数, 以及四个省缺为 "iRprop+" 的训练方法 (如上描述)。您可以毫无疑问地更改这两个参数和训练方法。这些函数很容易应用: 在 FineTuneDarch() 里改变微调函数
setFineTuneFunction(dbn) <- rpropagation
除了微调设置, 我们必须设置 (如有必要) 每层的激活神经元的函数。我们知道 sigmoidUnit 已在所有层省缺设置。软件包里可用函数 sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative。微调的定义将采用有能力选择微调函数的单独函数。我们将在单独的列表中收集可能的激活功能函数:
actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative)
我们将编写一个微调函数来训练和生成两个神经网络: 第一个 — 使用 backpropagation 函数训练, 第二个 — 采用 rpropagation:
#-----9----------------------------------------- fineMod <- function(variant=1, dbnin, dS, hd = 0.5, id = 0.2, act = c(2,1), nE = 10) { setDropoutOneMaskPerEpoch(dbnin) <- FALSE setDropoutHiddenLayers(dbnin) <- hd setDropoutInputLayer(dbnin) <- id layers <<- getLayers(dbnin) stopifnot(length(layers)==length(act)) if(variant < 0 || variant >2) {variant = 1} for(i in 1:length(layers)){ fun <- actFun %>% extract2(act[i]) layers[[i]][[2]] <- fun } setLayers(dbnin) <- layers if(variant == 1 || variant == 2){ # backpropagation if(variant == 2){# rpropagation #setDropoutHiddenLayers(dbnin) <- 0.0 setFineTuneFunction(dbnin) <- rpropagation } mod = fineTuneDArch(darch = dbnin, dataSet = dS, numEpochs = nE, bootstrap = T) return(mod) } }
一些有关函数的形式参数的澄清。
- variant - 选择微调函数 (1- backpropagation, 2- rpropagation)。
- dbnin - 从预训练接收结果的模式。
- dS - 用于微调的数据集合 (dataSet)。
- hd - 神经网络隐藏层的采样系数 (hiddenDropout)。
- id - 神经网络输入层的采样系数 (inputDropout)。
- act - 神经网络每一层神经元激活函数的指引向量。向量长度比层的数量短一个单位。
- nE - 训练周期的次数。
dataSet — 在此版本中出现的新变量。我真的不理解其出现的背后原因。正常的话, 语言有两种方式转换变量到模型 — 使用 pair (x, y) 或 formula (y~., data)。这个变量的引入并未改进品质, 但却令用户混淆。不过, 作者可能有不为人知的原因。
3.4. 测试模型。标尺。
在测试样品上进行训练模型测试。必须要考虑的是, 我们将计算两个标尺: 正式精确度和定性 K。相关信息将在下面提供。为此目的, 我们将需要两套不同的数据样本, 我将向您解释为什么。为了计算精度, 我们需要目标变量的值, 和之字折线, 如我们之前印象, 最后一根柱线常常没有定义。因此, 计算精度的测试样本我们确定将用 prepareTrain() 函数, 对于定性指标我们将使用以下函数
#---10------------------------------------------- prepareTest <- function(n, z, norm, len = 501) { x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% tail(., len) CO <- price[ ,"CO"] %>% tail(., len) if (norm) { x <- predict(prepr,x) } dt <- cbind(x = x, CO = CO) %>% as.data.frame() return(dt) }
模型将依据历史最后 500 根柱线进行测试。
为了实际测试, 将应用 testAcc() 和 testBal()。
#---11----- testAcc <- function(obj, typ = "bin"){ x.ts <- DT$test[ ,best] %>% as.matrix() y.ts <- DT$test$y %>% as.integer() %>% subtract(1) out <- predict(obj, newdata = x.ts, type = typ) if (soft){out <- max.col(out)-1} else {out %<>% as.vector()} acc <- length(y.ts[y.ts == out])/length(y.ts) %>% round(., digits = 4) return(list(Acc = acc, y.ts = y.ts, y = out)) } #---12----- testBal <- function(obj, typ = "bin") { require(fTrading) x <- DT.test[ ,best] CO <- DT.test$CO out <- predict(obj, newdata = x, type = typ) if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} sig <- ifelse(out == 0, -1, 1) sig1 <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig1 * tail(CO, length(sig1))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- maxDrawDown(bal) return(list(sig = sig, bal = bal, K = K, Kmax = Kmax, dd = dd)) }
第一个函数返回 Acc 和目标变量值 (实际或预测) 用于可能的进一步分析。第二函数返回用于 EA 的预测信号 sig , 所获平衡基于这些信号 (bal), 品质系数 (К), 在测试区域的系数最大值 (Kmax) 以及同一区域的最大回撤 (dd)。
当计算平衡时, 要记住的重要是, 最后预测信号指向尚未形成的未来柱线, 因此, 应该在计算时将其删除。我们已经通过将 sig 向量右移一根柱线来解决它。
3.4.1. 预测解码。
所获结果可使用 "WTA" 方法解码 (从矩阵转换为向量)。分级等于具有最大概率值的列数, 并概率的阈值可以设置, 低于阈值时分级不可确定。
out <- classmat2classvec(out, threshold = 0.5) 或 out <- max.col(out)-1
如果阈值设置为 0.5, 且列中最大的概率低于此阈值, 我们将获得一个附加分级 ("未定义")。当计算像是 Accuracy 矩阵时应予以考虑。
3.4.2. 改善预测结果
是否可能在接收到预测结果后改进预测结果?有三种可能的方法可以应用。
- 校验
CORElearn::calibrate(correctClass, predictedProb, class1 = 1, method = c("isoReg", "binIsoReg", "binning", "mdlMerge"), weight=NULL, noBins=10, assumeProbabilities=FALSE)
此处:
- correctClass — 对于问题分类的正确分级标签向量;
- predictedProb — 与 correctClass 长度相同的预测分级 1 (概率) 的向量;
- method — 以下之一 ("isoReg", "binIsoReg", "binning", "mdlMerge")。更多信息, 请阅读软件包说明;
- weight — 向量 (如果指明) 必须与 correctClass 长度相同, 且为每次观测提供权重, 否则所有观测权重省缺等于 1;
- noBins — 根据 method 的参数值, 并确定期望的或初始通道的数量;
- assumeProbabilities — 逻辑, 若是 TRUE, 则在 predictedProb 中数值的期待范围 [0, 1], 即, 作为可能性评估, 否则算法可用作简单的等张回归。
此方法适用于由向量设置的两个级别的目标变量。
- 使用马尔科夫链模型平滑预测结果
这是一个广泛而复杂的课题, 值得一篇单独的文章, 因此我不会深入理论, 仅提供最基本的信息。
马尔科夫过程 — 是具有以下特征的随机过程: 对于任何时间点 t0, 未来系统任何状态的概率仅取决于其当时的状态, 并且不依赖于系统何时以及如何到达该状态。
随机马尔科夫过程的分类:
- 具有离散状态和离散时间 (马尔科夫链);
- 具有连续状态和离散时间 (马尔科夫一致性);
- 具有离散状态和连续时间 (连续马尔科夫链);
- 具有连续状态和连续时间。
在此仅考虑具有离散状态 S1, S2, ..., Sn. 的马尔科夫过程。
马尔科夫链 — 具有离散状态和离散时间的马尔科夫过程。
时刻 t1, t2, ... 当 S 系统可以改变其状态时被认为是该过程的后续步骤。它不是 t 时间, 但步骤编号 1,2,...,k,...被进程用作所依赖的参数。
随机过程的特征在于状态序列 S(0), S(1), S(2), ..., S(k), ..., 此处 S(0) 是初始状态 (第一步之前); S(1) — 第一步之后的状态; S(k) — 系统在第 k 步之后的状态。
马尔科夫链状态的概率 是 Pi(k) , 它是 k 步之后 (以及 (k + 1) 步之前) 的概率, S 系统将处于 Si(i = 1 , 2 , ..., n) 状态。
马尔科夫链概率的初始分布 — 在过程开始时状态概率的分布。
转移的概率 (转移概率) 在第 k 步从 Si 状态到 Sj 状态 — 条件概率, S 系统在 k 步之后将出现 Sj 状态, 条件是在 (k—1 步) 之后处于 Si 状态。
统一马尔科夫链的转移概率 Рij 来自 一个 n х n 尺寸的正方形矩阵。它有以下特点:
- 每一行描述系统所选的状态, 及其元素 — 在一步之中所有可能的转移概率来自选择的 (从 i 编号) 状态。
- 列的元素 — 在一步之中所有可能的转移概率至集合 (j) 状态。
- 每行的概率总和等于一。
- 在主对角线 — Рij 概率, 系统不会从 Si 状态退出, 依然会保留。
马尔科夫过程可被观测和隐藏。隐藏马尔科夫模型 (HMM) 由一对离散随机震荡过程 {St} 和 {Xt} 组成。可观测过程 {Xt} 经所谓的条件分布与不可观测 (隐藏) 的状态 {St} 马尔科夫过程相链接。
严格地讲, 我们的目标时间序列, 其可观察状态 (分级) 马尔可夫过程是不统一的。很明显, 转移概率从一个状态到另一个状态取决于当时状态所花费的时间。这意味着在改变状态之后的第一步期间, 其变化的概率较低, 且随状态花费时间的增加而增长。这些模型称为半马尔科夫 (HSMM)。我们不会深入分析它们。
但思路如下: 基于从之字折线获得的理想信号 (目标) 的离散阶数, 我们将发现 НММ 的参数。然后, 通过神经网络预测的信号, 我们使用 НММ 将之平滑。
它会给我们带来什么?正常地话, 在神经网络预测中存在所谓的 "发散", 状态变化的区域为 1-2 根柱线长。我们知道目标变量没有这么短的长度。通过在目标变量上应用获得的模型来预测顺序, 我们可将其带至更可能的转移。
我们将使用专为计算隐藏马尔科夫和半马尔可夫模型而设计的 "mhsmm" 软件包来进行这些计算。我们将使用 smooth.discrete() 函数, 简单地对离散值的时间序列进行平滑。
obj <- smooth.discrete(y)
省缺在结尾得到平滑状态顺序 — 由于更喜欢使用 Viterbi 算法 (所谓全局解码) 来获取状态顺序。. 还有一个选项可使用其它方法 — smoothed, 在此识别单独的最可能状态 (所谓局解码)。
应用标准方法来平滑新的时间序列
sm.y <- predict(obj, x = new.y)
- 在理论性平衡曲线上校正预测信号
概念如下。已有平衡线, 我们可以计算其与平均线的偏差。使用这些偏差, 我们会计算校正信号。在偏差为负的时刻, 即可禁止执行预测信号, 或将它们逆转。这个想法通常很好, 但有一个缺点。零号柱线有一个预测信号, 但它没有平衡值, 因此没有校正信号。有两种方式来解决这个问题: 通过分类 — 基于存在的调整信号和偏离预测调整信号; 通过回归 — 使用已形成的柱线上的偏离来预测新柱线上的偏离, 并在其基础上识别调整信号。有一个更容易的解决方案, 您可在已形成的基础上获取新柱线的调整信号。
由于上述方法已为我们所知, 并且已测试过, 我们将尝试实现马尔科夫链的机会。最近出现的 "马尔科夫链" 软件包含有一系列函数, 可以确定隐藏马尔科夫模型的参数, 并通过观察随后若干根柱线的离散过程来投影未来状态。这个思路来自这篇 文章。
3.4.3. 标尺
为了评估模型预测的品质, 整个标尺范围 (Accuracy, AUC, ROC 和其它) 将要用到。在前文中我提到, 在我们的情况下, 正式的标尺不能定义品质。智能交易系统的目标是在可接受回撤内攫取最大利润。为此目的, 引入 K 品质指标, 并且它会显示历史片段上固定 N 长度的每根柱线平均利润点数。计算是通过累积 Return(sig, N) 再除以 N 段的长度。计算的 Accuracy 仅用于指示。
最后, 我们执行计算并得到测试结果:
- 输出数据。我们已有了 price[] 矩阵, 作为 price.OHLC() 函数的执行结果得到。它包含报价, 均价和柱线实体。所有输出数据可通过下载 Rstudio 附件中出现的 "图标" 来获得。
# 查找常数 n = 34; z = 37; cut = 0.9; soft = TRUE. # 查找预处理方法 method = c("center", "scale","spatialSign") # 来自初始数据集合 data.f <- form.data(n = n, z = z) # 查找重要预测器集合 best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) # 计算在 2-核处理器上大约要花费 3 分钟。若您愿意, 您可以跳过此阶段, # 并在将来使用整个预测器集合。所以, 注释前行并 # 取消底下两行的注释。 # data.f <- form.data(n = n, z = z) # best <- colnames(data.f) %>% head(., ncol(data.f) - 1) # 准备训练神经网络的集合 DT <- prepareTrain(x = data.f[ , best], y = data.f$y, balance = TRUE, rati = 501, mod = "stratified", norm = TRUE, meth = method) # 下载所需库文件 require(darch) require(foreach) # 识别可用激活函数 actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative) # 转换目标变量 if (soft) { y <- DT$train$y %>% classvec2classmat()} # 至矩阵 if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # 到值为 [0, 1] 的向量 # 创建用于训练的 dataSet dataSet <- createDataSet( data = DT$train[ ,best] %>% as.matrix(), targets = y , scale = F ) # 识别神经网络常数 # 每个输入层的神经元数量 (等于预测器数额) nIn <- ncol(dataSet@data) # 输出层的神经元数量 nOut <- ncol(dataSet@targets) # 拥有神经网络每一层神经元数量的向量 # 如果您使用另一种神经网络结构, 这个向量应该重写 Layers = c(nIn, 2 * nIn , nOut) # 其它训练相关的数据 Bath = 50 nEp = 100 ncd = 1 # 神经网络预训练 preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd) # 微调的附加参数 Hid = 0.5; Ind = 0.2; nEp = 10 # 训练两个模型, 一个与反向传播, 其它正常传播 # 我们只做这个来比较结果 model <- foreach(i = 1:2, .packages = "darch") %do% { dbn <- preMod if (!soft) {act = c(2, 1)} if (soft) {act = c(2, 4)} fineMod(variant = i, dbnin = dbn, hd = Hid, id = Ind, dS = dataSet, act = act, nE = nEp) } # 测试得到 Accuracy resAcc <- foreach(i = 1:2, .packages = "darch") %do% { testAcc(model[[i]]) } # 准备数据样本来测试品质系数 DT.test <- prepareTest(n = n, z = z, T) # 测试 resBal <- foreach(i = 1:2, .packages = "darch") %do% { testBal(model[[i]]) }
让我们看看结果:
> resAcc[[1]]$Acc [1] 0.5728543 > resAcc[[2]]$Acc [1] 0.5728543
对于两个模型它同样不佳。
至于品质系数:
> resBal[[1]]$K [1] 5.8 > resBal[[1]]$Kmax [1] 20.33673 > resBal[[2]]$Kmax [1] 20.33673 > resBal[[2]]$K [1] 5.8
它表现出相同的良好性能。然而, 大幅回撤令人担忧:
> resBal[[1]]$dd$maxdrawdown [1] 0.02767
我们将尝试使用来自以下计算获得的校正信号来调整回撤:
bal <- resBal[[1]]$bal # 信号位于最后 500 根柱线 sig <- resBal[[1]]$sig[1:500] # 来自平衡曲线的均值 ma <- pracma::movavg(bal,16, "t") # 来自均值的动量 roc <- TTR::momentum(ma, 3)%>% na.omit # 平衡线自均线的偏离 dbal <- (bal - ma) %>% tail(., length(roc)) # 两个向量汇总 dbr <- (roc + dbal) %>% as.matrix() # 计算调整信号 sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) gives the same result # 结果信号 S <- sig.cor * tail(sig, length(sig.cor)) # 在结果信号上的平衡 Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S)))) # 在调整信号上的品质系数 Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig > Kk [1] 28.30382
校正信号基础上所示的品质结果非常好。让我们看看如何使用 dbal, roc 和 dbr 来计算出现在折线图表上的调整信号 。
matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1)) abline(h=0, col=2) grid()
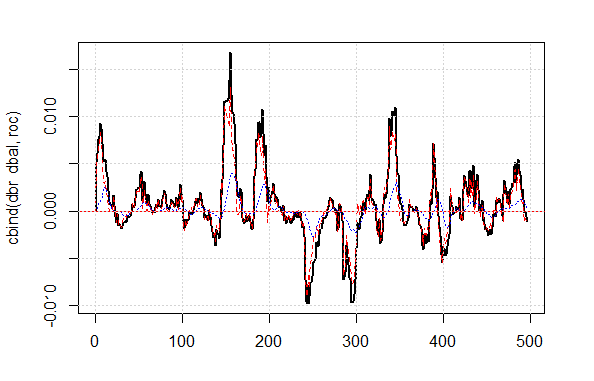
图例.4 平衡线自均线的偏离
信号调整之前和之后的平衡线示意如图例. 5.
plot(c(NA,NA,NA,Bal), t="l") lines(bal, col= 2) lines(ma, col= 4)
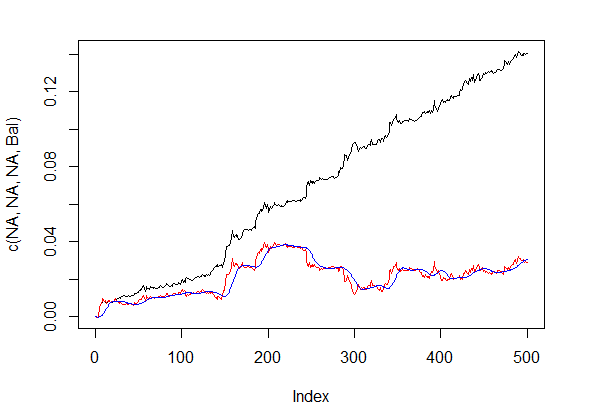
图例.5 信号调整之前和之后的平衡线
所以, 我们在零号柱线上已经有了经过神经网络预测的信号值, 但没有调整值。我们想使用隐藏马尔科夫模型来预测这个信号。基于观测到的调整信号的状态, 我们用最后几个状态来识别模型的参数, 预测前一根柱线的状态。首先, 我们将编写 correct() 函数, 它将基于已预测的, 结果信号和其品质指标来计算调整信号。换言之, 我们要赶紧记下之前执行的计算。
我希望澄清一下: 本文中的 "信号" 是一个整数 -1 和 1 的序列。"状态" 是对应于这些信号的整数 1 和 2 的序列。为了相互转换, 我们将使用函数:
#---13---------------------------------- sig2stat <- function(x) {x %>% as.factor %>% as.numeric} stat2sig <- function(x) ifelse(x==1, -1, 1) #----14--调整----------------------------------- correct <- function(sig){ sig <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig)))) ma <- pracma::movavg(bal, 16, "t") roc <- TTR::momentum(ma, 3)%>% na.omit dbal <- (bal - ma) %>% tail(., length(roc)) dbr <- (roc + dbal) %>% as.matrix() sig.cor <- sign(dbr) S <- sig.cor * tail(sig, length(sig.cor)) bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S)))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- fTrading::maxDrawDown(bal) corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd) return(corr) }
为了获得前一根柱线的预测信号向量, 我们将使用 "markovchain" 软件包和 pred.sig() 函数。
#---15---马尔科夫链---------------------------------- pred.sig <- function(sig, prev.bar = 10, nahead = 1){ require(markovchain) # 将观察到的校正信号转换为状态 stat <- sig2stat(sig) # 计算模型参数 # 如果在环境中没有模型 if(!exists('MCbsp')){ MCbsp <<- markovchainFit(data = stat, method = "bootstrap", nboot = 10L, name="Bootstrap MС") } # 设置必要常数 newData <- tail(stat, prev.bar) pr <- predict(object = MCbsp$estimate, newdata = newData, n.ahead = nahead) # 将预测信号挂载到输入信号 sig.pr <- c(sig, stat2sig(pr)) return(sig.pr = sig.pr) }
现在, 我们将记录计算结果信号, 供智能交易系统简洁地执行:
sig <- resBal[[1]]$sig sig.cor <- correct(sig) sig.c <- sig.cor$sig.c pr.sig.cor <- pred.sig(sig.c) sig.pr <- pr.sig.cor$sig.pr # 用于智能交易系统的信号结果向量 S <- sig.pr * tail(sig, length(sig.pr))
- 平滑预测信号。
#---16---平滑------------------------------------
smoooth <- function(sig){
# 平滑预测信号
# 定义隐藏马尔科夫模型的参数
# 如果环境中尚无模型
require(mhsmm)
if(!exists('obj.sm')){
obj.sm <<- sig2stat(sig)%>% smooth.discrete()
}
# 用所获模型平滑信号
sig.s <- predict(obj.sm, x = sig2stat(sig))%>%
extract2(1)%>% stat2sig()
# 用平滑信号计算平衡
sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
K <- tail(bal, 1)/length(bal) * 10 ^ Dig
Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
dd <- fTrading::maxDrawDown(bal)
return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}
我们将根据已预测和已平滑的信号进行平衡的计算和比较。
sig <- resBal[[1]]$sig sig.sm <- smoooth(sig) plot(sig.sm$bal, t="l") lines(resBal[[1]]$bal, col=2)
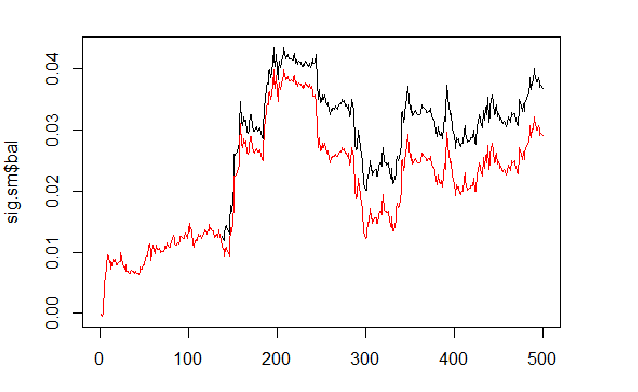
图例.6 基于平滑和预测信号的平衡
正如我们所见, 品质略有提高, 但回撤仍然存在。我们将不会在我们的智能交易系统中使用此方法。
sig.sm$dd $maxdrawdown [1] 0.02335 $from [1] 208 $to [1] 300
4. EA 算法的结构
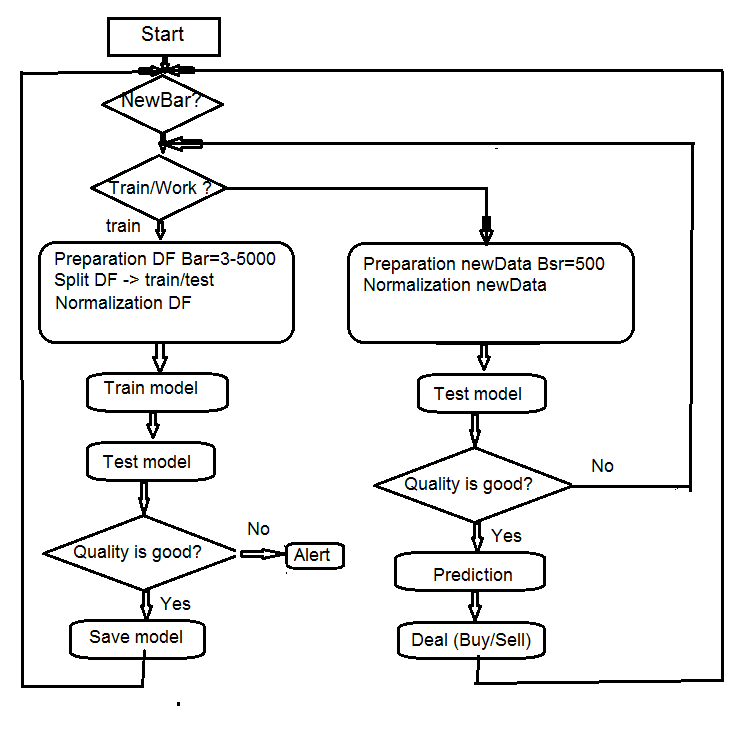
图例.7 EA 算法的结构
4.1. 智能交易程序操作的描述
由于智能交易系统是在两个流 (mql 和 Rterm) 中操作, 我们将描述它们的交互过程。我们将分别讨论每个流中执行的操作。
4.1.1 MQL
将智能交易系统置于图表上之后:
在 init() 函数里
- 我们检查终端的设置 (DLL 可用, 授权交易);
- 设置定时器;
- 启动 Rterm;
- 计算并传递所需工作常量至 R-过程环境;
- 检查 Rterm 是否工作, 如果没有 - 报警;
- 从 init() 退出。
在 deinit() 函数里
- 我们停止定时器;
- 删除图形对象;
- 停止 Rterm。
在 onTimer()函数里
- 检查 Rterm 是否正在工作;
- 如果 Rterm 未占据且 新柱线 是 (LastTime != Time[0]):
- 根据是否为首次启动 EA, 设置历史深度;
- 形成四个报价向量 (开盘价, 最高价, 最低价, 收盘价) 并将它们传递进 Rterm;
- 启动脚本并离开, 无需接收其执行结果;
- 设置 get_sig = true 标志;
- 设置 LastTime= Time[0]。
- 否则, 若 Rterm 工作, 未占据且标志为 get_sig = true:
- 识别我们将从 Rterm 接收的 sig 向量的长度;
- 将接收向量的大小调整为源头的大小。当不可遵守时, Rprocess 将遗弃;
- 获取信号的顺序 (向量);
- 使用最后的信号来判定哪个操作已执行 (买入, 卖出, 无);
- 如果我们获得真实信号, 非 ERR, 我们会重置标志为 get_sig=false。
- 其余的为标准:
- CheckForClose()
- CheckForOpen()
在这一部分, 我们的系统是一个"执行者", 落实获自其 "思考" 部分的命令, 发送订单, 跟踪开仓状态以及开仓时可能的错误, 并执行标准智能交易系统的许多其它功能。
4.1.2 Rterm
操作脚本由两部分组成。第一部分在首次入场时执行, 第二部分 - 在以下情况。
- 如果 首次:
- 从互联网上的存储库中加载 (若需要) 必要库文件, 并将它们安装到 Rterm 环境;
- 定义必要函数;
- 创建报价矩阵;
- 准备用于训练和测试模型的数据样本;
- 创建和训练模型;
- 测试模型;
- 计算执行信号;
- 检查预测品质。如果它高于或等于所设置的最小值 — 处理。否则 — 发送警报。
- 如果 非首次:
- 准备用于测试和预测的数据样本;
- 在新数据上测试模型;
- 计算执行信号;
- 检查预测品质。如果它超出或等于所设置的最小值 — 我们处理。否则 — 我们设置 first = TRUE, 即, 我们请求重新训练模型。
4.2. 自控制和自训练
模型预测信号的品质控制使用 К 系数进行。有两种方法来识别可接受品质的限制。首先 — 设置最大相对其最大值的回落系数。如果 К < Kmax * 0.8, 则我们应重新训练, 或停止智能交易系统在信号出现时的操作。其次 — 设置 К 的最大值, 达到之后需要相同的动作。我们将在 EA 中使用第二种方法。
5. 安装和启动
本文附带了两个: e_DNSAE.mq4 和 e_DNRBM.mq4。它们都使用相同的数据样本, 以及几乎相同的一套函数。区别在于使用的深度网络模型。第一个 EA 使用DN, 初始 SAE 和 "deepnet" 软件包。软件包的描述可以在上一篇关于深层神经网络的文章中找到。第二个 EA 使用DN, 初始 RBM 和 "darch" 软件包。
应用标准发布:
- *.mq4 在 ~/MQL4/Expert 文件夹
- *.mqh 在 ~/MQL4/Include 文件夹
- *.dll 在 ~/MQL4/Libraries 文件夹
- *.r 在 C:/RData 文件夹
我们调整了设置 R 语言和脚本的路径 (mq4: #define 和 *.r: source() 均包括)。
当第一次启动 EA 时, 它将从存储库下载必要的库文件, 并在 Rterm 环境中设置它们。您也可以根据所附的列表提前安装它们。
通常, R 过程会由于缺乏必要库文件、错误地路径指示、以及脚本的语法错误而被明确地 "放弃"。
单独附加了初始数据的会话截图, 您可以用 Rstudio 打开它, 以检查所有功能是否都正常工作, 并进行实验。
6. 改进定性指标的方式方法。
有几种方法来改进定性指标。
- 预测器的评估和选择 — 应用遗传算法优化 (GA)。
- 确定预测器和目标变量的最优参数 — GA。
- 确定神经网络的最优参数 — GA。
结论
使用 "darch" 软件包的实验已经显示出以下结果。
- 深层神经网络, 初始 RBM 训练结果比 SAE 更差。这对我们来说并非新闻。
- 网络被快速训练。
- 通过对模型的几乎所有内部参数提供访问, 软件包具有改进预测品质的巨大潜力。
- 软件包仅可用在具有更广泛参数集合的神经网络或 RBM (相对其它标准的)。
- 软件包正在不断发展, 开发人员承诺在下一个版本中引入更多功能。
- R 语言与 МТ4/МТ5 终端的集成, 如开发者承诺, 将为交易者提供机会来使用最新的算法而无需额外的 DLL。
附件
- R 语言的 Sess_DNRBM_GBPUSD_30 会话过程
- "e_DNRBM" 智能交易系统的 ZIP 文件
- "e_DNSAE" 智能交易系统的 ZIP 文件


