很难说明为什么马丁格尔一词有如此多的含义。但有一点是毫无疑问的：如果交易者使用马丁格尔策略，它对交易者的押金至关重要。马丁格尔赌博策略有哪些优势和劣势？如何能够在策略中抓住尖峰？市场是马丁格尔吗？将在本文中讨论上述所有问题以及其他一些密切关联和相互关联的问题。

词源

马丁格尔是 martegal （法国方言词语，含义为 Martigues 的居民；Martigues 是或者曾经是法国的一个村庄）的英文形式。马丁格尔最早的时候应该是指马身上用于控制马车的马具。此含义至少是最广为人知的含义，但对我们而言，另一个含义更为重要，即：马丁格尔是一种赌博策略。每次输钱后，赌博者都会将其赌注翻倍，因此，只要赢一次，就可以将之前亏损的全部金额赢回来，还会赢得等同于初始本金的金额。交易者也将为所有相关策略取这个名词。此外，数学家使用马丁格尔一词命名一种随机过程，在此过程中，已假定当前值和之前的值，下一个值的条件期望值为当前值。它是一种“公平游戏”，在此游戏中，没有人输，也没有人赢。至于法国的 Martigues 村庄，该村庄的居民曾被视为一群古怪而很可能爱冒险的人。总之，如此多的含义有时会成为导致一些人用错的原因。那么，什么是马丁格尔？

马丁格尔作为一种策略

那么，邦德使用了哪种累进制？如前所述，马丁格尔意味着在赌博游戏（例如轮盘赌）中输钱后会将初始本金翻倍。乍看起来，如果没有赌注限制，此策略似乎有利 可图。交易者肯定会有幸运的一天！尽管此策略看起来非常基本，然而，这世界并没有很多通过使用轮盘赌而变富的人。那么，这究竟是怎么回事？如果从小赌注开始，即便我们没有无限的钱，我们最终也 可以一直坚持很久！

这种或类似逻辑会让不明智的人急于尝试该策略，押注他们全部的钱。但并不适用于轮盘赌，完全不适用！一些人已经认识到这一点，因此他们不会去参与几率游戏。他们在外汇市场上尝试使用此策略。这些人更聪明、更具冒险精神，往往也会用别人的钱试验此策略。因此，新型的交易骗子开始出现。获利交易与亏损交易交替出现，但是，由于赌注翻倍，玩家偶尔会赢钱。这会令交易者相信自己的选择。但是，迟早（为了交易者的健康，越早发生越好…）会出现连续的霉运使他没有钱来将押注翻倍。结果是，浩瀚的互联网世界中又将出现一个更加不幸的人。一个失落的交易者，“在就要赢钱时却没有资金了”，“被纯粹的坏运气所打败”。如果不是“因为经纪人给出了错误的报价”，就是件好事。

说真的，没有很多交易者会相信经典马丁格尔。然而，不能低估一些冒险家的愚蠢。将用到更加复杂的方法，这些方法通常被称为“尖峰”。含义如下：假定您要面临以下选择：赢 1 美元的概率为 99%，输 99 美元的概率为 1%。该交易的平均值结果当然为零。通常，这不具有盈利性，而且有风险！无关紧要的获利需要承担惨重的损失和干扰（这就是此处为什么使用“尖峰”的原因）。在外汇市场上做此类交易极其简单：如果您设置的止损点比获利点高 99 倍，您将获得类似的结果。这不现实吗？但是，我们看到的是，很多交易者的止损点与获利点不相称甚至于完全不相关（多么可怕！）。

当然，主要危害不是上述情况。想象一下：某个人想测试或监控此类“专家”。在多数情况下，一个人在损失惨重以致再也不能交易之前，可进行多少次获利交易。他在多久之后会抱怨自己“不幸”以及多久之后会“在最后一刻没有钱可以下注”。

然而，问题不仅仅是没有止损订单。尖峰和没有止损还伴随着头寸停留过久。在这段时间内，价格有时会非常之高。

但是，基于马丁格尔的“圣杯”专家一次又一次反复出现，很多人在论坛上很严肃地讨论这种交易方法。为什么？包括不相称的止损、本金翻倍、停留时间过长和其他类似技巧的策略被试验证实为一种绝对不可靠的方式。从实际经验中得出，可针对特定历史背景轻松制定此类策略，并获得良好的成果。用在一个真实的帐户上，此策略可使用一周、一个月、一年时间，可进行 10 次、20 次或 50 次交易，只要有一点运气，就可以获得良好/极佳的成果。而唯一的错误交易会让他们输光所有钱。那么什么将这些策略联系起来的？

马丁格尔作为一个过程

实际上，数学家知道马丁格尔的时间并不久远。有关马丁格尔的第一篇数学描述是在 20 世纪中期发布的。创作者的灵感来自于希望概括无佣金的轮盘赌、、骰子或抛硬币等“公平赌博”这一概念，，本文稍后将介绍该内容。在广阔的网络世界里，可以找到很多有关马丁格尔的不同定义！如果没有掌握重要的理论装备，即便是了解正式的定义，也无事于补。因此，我们尝试在此处提供一个简单而又十分严谨的定义：马丁格尔是一个过程，在此期间，不会随着时间向上或向下波动。因此，如果我们想要基于所有之前的值预测下一个值，没有比当前值更好的值了（在均方值方面）。

必须指出，有关货币兑换率波动是否类似于马丁格尔的问题非常重要。然而，统计观察结果会很快针对此问题提供否定的回答。例如，货币率增量之间没有关联性。这一预设构成了很多古典和新古典模型（Bachelier、Black-Sholes-Merton 等）的基础，并可得出有关衍生产品（期权、远期合约等）行为具有深远意义的结论。除此之外，马丁格尔术语非常适应 “公平地”定义每个时刻的价格的有效市场概念。因此，它在经济上是合理的。

马丁格尔理论的其中一个基础是有关停止和进一步构建随机积分的定理。该定理说明，要使用马丁格尔赚钱，并没有合理的策略。严肃的读者不禁会问，为什么会如此？马丁格尔策略有什么问题？该定理为什么会认为马丁格尔“不合理”而将其抛弃？问题是，最合理的策略对价格（用外汇术语“发出止损订单”更为清楚）或时间进行限制，即范围固定，当达到该限值时一定会结束交易。最重要的事情是，它们都在押注（每次交易的金额、手数等）方面有限制。任何能够同时满足前两个条件中的任一个条件和第三个条件的策略始终是“合理的”策略。很多其他策略也都是“合理的”策略，但是现在我们不想讨论技术细节。马丁格尔策略有三个缺点：第一点，押注没有限制；第二点，时间没有限制；最后，“马丁格尔”玩家将巨额亏损。此示例很好地说明了，由于筹码和押注时间没有限制，使用此方法赢不了任何钱。它还有助于理解即便在简单的游戏中也可以模拟“可获利的”策略！

然而，让我们回到现实，用一些简单的例子来阐述上述整个理论。

示例

让我们设想使用均衡的硬币进行抛掷游戏，即硬币的正面和反面概率相等。假定一下，如果是正面，则玩家 B 向玩家 A 支付一卢布；如果是反面，则玩家 A 向玩家 B 支付一卢布。下面是 A 的本金基于所作出的抛掷次数的典型演进（图 1）– 概率路径（蓝色和红色）。

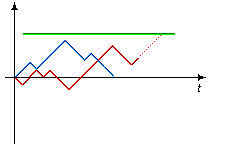
图 1

平均来说，抛掷硬币时玩家不会赢也不会输，在这个意义上讲，其中一个玩家（我们不知道是哪位玩家）一定会赢一卢布，而另一个玩家一定会输一卢布。有关他们的本金变化的数学期望值等于零。此示例以及不受约束的硬币抛掷说明了，玩家 A 的本金增加为马丁格尔。同时，这还可得出很多结论。例如，有关该赌博是公平赌博的结论，在这个意义上，从统计角度上讲在这样的赌博中无法赢钱，即任何止损策略的平均值都将为零。让我们的玩家使用固定金额，同时谨记马丁格尔结果。该理论说明了，他使用任何合理的方法都无法赢钱。您可能会问为什么会这样？玩家可以等待直到“有盈利”，然后停止玩游戏（图 1 中的绿色“获利”级别）。是的，但不幸的是，尽管有时会出现此情况，但平均来说，他要等待很长时间才会出现。严格说来，获利时间的数学期望值等于无穷大，并不适合“合理的策略”概念。而且，如果他依然决定“承受”损失，当他最后停下来时，他的亏损将非常巨大。发现交易新手往往会出现这种情况。

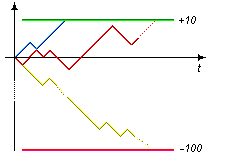
图 2

但是，我们的玩家并没有这么简单！根据上述提及的所有内容，他设定了一个“很大的”止损点和一个“很小的”获利点，如图 2 所示。现在本金受到限制，他的策略变成了“合理的”策略。当他尝试试验时，此策略能够在长时间内大把赚钱，尤其是抛硬币无须支付佣金。那么，这究竟是怎么回事？此定理真的不正确？不，它仍然有效！如果您仅使用此定理进行仔细计算，例如计算获利或止损概率，由于 10 例中有 9 例使用小获利，而 10 例中仅 1 例大亏损，因此结果是只不过出现尖峰。对于玩家而言，此类风险的推迟的成本高昂，他会在一天之内倾家荡产。

抛硬币示例尽管很原始，但仍反映冒险性资金管理或马丁格尔策略的幕后动机。事实上，我们只是给我们的头寸增加了纯粹的风险，而没有别的东西。

因此，让我们来总结上述内容。

总结

一切都没问题，但是如上所述，市场不是马丁格尔。最终，除赚钱目的以外，外汇交易的重点是什么？那么实际交易的所有这些理论结果都是由什么产生的？重点是，有更多的方法来通过提供“可获利的”（至少第一眼看上去）策略欺骗自己或观察者，即便是处于几率路径示例那样的理论上无法赢钱的情况下。难怪使用相同的策略频繁创建“圣杯”和诱捕投资者。但是，只要牢记马丁格尔/尖峰理论，就可以逃离很多幻想。

现在让我们来基于本文制定一些理性交易规则。如果您不希望系统被过往所蒙混、遭受巨大亏损和引起潜在投资者的怀疑，请遵守以下规则：

• 设定止损（止损/获利）；
• 尝试设定与获利和时长成比例的止损；
• 不要停留头寸过长时间，与交易时间范围不成比例 – 从交易开始后，时间范围将随着时间的流逝而“缩短”，或者换种方式，在这种情况下，有很多方法；
• 不要增加试图弥补损失的金额 – 不要效仿在赌场中孤注一掷的人（也不要效仿上面的邦德）！

上述规则并不严格。在大多数的策略制定中，头寸根本不是由止损或获利所取消的。必须指出，在这里我们可以获得获利交易平均利润或亏损交易平均损失，或者将投资额与交易的潜在风险级别相关联。然而，上述规则应被视为专门用于提高 Expert Advisor 的清晰度和透明度，以及总体上适用于提高策略的清晰度和透明度。交易者，尤其是交易新手，应坚持此观点。

最后我想对有兴趣的读者说一个问题，此问题可追溯到 Daniel Bernoulli 和 18 世纪。它就是所谓的圣彼得堡悖论。假定 X 正在玩一场这样的游戏：押注为 1 卢布。抛掷一个均衡的硬币。如果是正面朝上，则停止游戏，X 将获得押注。如果是反面朝上，押注将翻倍，以此类推：抛掷硬币，如果正面朝上则停止游戏、拿钱，如果是反面朝上，则押注翻倍再次抛掷...问题：X 应支付多少钱来玩此游戏？可以看出，在这场游戏中 X 始终会赢，但金额取决于硬币是正面还是反面朝上。换言之，在没有先例的情况下，您会支付多少钱来参与这场充满吸引力的慷慨游戏？如果此问题激发起好奇心，将在备注中讨论其解决方案。