概论
每天我们都会从全球市场上读到多种财经消息, 包含诸如此类的短语 "美元兑主要货币疲软..." 这意味着一种货币的状态相对一组其它货币已发生了改变。这种动词结构的使用惯例是要生成完整的货币对列表, 并将它们切分为组和子组。
致力于将品种划分为组或是 "篮子" 的各种方法资料在各处交易论坛上也是屡见不鲜。货币对化分为 "篮子" 后, 便可精确分析 "篮子" 中彼此相邻品种的协同行为。假设这些货币对的通常行为以类似方式在大致相同的时刻形成极值, 并近乎以同向移动。这样的一个品种组 (或一个"篮子") 表现为一个虚拟货币对的均值, 并可适当地进行分析。
原理和定义
完整的思路是基于属性的重要性为交易者重组货币对。一些这样的属性对于大家是众所周知的, 例如油价和卢布汇率之间的关联性, 或是欧元兑美元和美元兑瑞郎之间的关联性。所以, 我们可以将它们组合为一个组 (货币篮子)。定义篮子的内容之后, 我们可以规划它可能的行动, 包括同时影响篮子内所有货币对 (在我们的例中这些是 EURUSD 和 USDCHF) 的行动。我们既可跟踪货币对的 "行为", 也可进行交易操作。
买入或卖出货币篮子涉及篮内每个货币的同时交易操作。在此情况下, 反向篮子指向的订单基于 "一个货币对 — 一笔订单" 的原则组成。所执行的交易操作条件, 表征货币篮子的状态。
货币对分组的原理自然且明显, 可应用于进一步的运作。所有 28 种主要货币对应根据当前每个货币对自身的基准货币 (或报价货币) 划分到篮子中。篮子的命名依据基准货币 (参见表 1 的示例)。在此情况下, 篮子状态由它的基准货币状态定义。状态参数包括超买/超卖状态, 和其它类似的属性。它们依照同样的技术分析手段提供, 我们用它来评估正常的货币对。
主要的货币篮子
让我们根据上述的原则来划分完整的货币对池子。其结果是, 我们得到 8 个货币篮子, 每个包含 7 种货币对:
| 编号 | 篮子名 | 篮子货币 | 篮子货币对 |
|---|---|---|---|
| 1 |
澳元篮子 |
AUD |
AUDUSD, AUDNZD, AUDJPY, AUDCAD, AUDCHF, EURAUD, GBPAUD |
| 2 |
加元篮子 |
CAD |
USDCAD, AUDCAD, NZDCAD, GBPCAD, EURCAD, CADCHF, CADJPY |
| 3 |
瑞郎篮子 |
CHF |
CHFJPY, USDCHF, GBPCHF, EURCHF, AUDCHF, NZDCHF, CADCHF |
| 4 |
欧元篮子 |
EUR |
EURUSD, EURJPY, EURCHF, EURGBP, EURNZD, EURCAD, EURAUD |
| 5 |
英镑篮子 |
GBP |
EURGBP, GBPAUD, GBPCAD, GBPCHF, GBPJPY, GBPNZD, GBPUSD |
| 6 |
日元篮子 |
JPY |
AUDJPY, CADJPY, CHFJPY, EURJPY, GBPJPY, NZDJPY, USDJPY |
| 7 |
纽元篮子 |
NZD |
NZDUSD, AUDNZD, NZDJPY, NZDCAD, NZDCHF, EURNZD, GBPNZD |
| 8 |
美元篮子 |
USD |
EURUSD, GBPUSD, AUDUSD, NZDUSD, USDCAD, USDCHF, USDJPY |
表 1. 货币篮子
现在, 我们已定义了篮子的内容, 是时候来澄清它们的主要交易操作了。让我们来假设买入和卖出一个篮子, 意指买入和卖出其内的货币。
假定有关日元的利好消息到达暗示其可能走强。一位交易员决定买入 JPY。根据我们的范例, 这位交易员应做空所有货币对来买入 JPY 篮子。在相反的情况下, 交易员应做多篮内所有货币对来卖出 JPY 篮子。
当处理 EUR 篮子时, 情况看来不会那么困惑。如果交易员打算买入 EUR 篮子, 做多其内所有货币对, 反之亦然。对于 EUR 和 JPY, 篮内订单均由单向订单组成。
让我们依照下表安排, 以避免交易操作混淆:
| 编号 | 篮子名 | 篮内货币交易操作 |
篮内货币对交易操作 | ||||||
|---|---|---|---|---|---|---|---|---|---|
1 |
澳元篮子 |
|
AUDUSD | AUDNZD | AUDJPY | AUDCAD | AUDCHF | EURAUD | GBPAUD |
| 做空 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 买入 | 买入 | ||
| 做多 | 买入 | 买入 | 买入 | 买入 | 买入 | 卖出 | 卖出 | ||
2 |
加元篮子 |
|
USDCAD | AUDCAD | NZDCAD | GBPCAD | EURCAD | CADCHF | CADJPY |
| 做空 | 买入 | 买入 | 买入 | 买入 | 买入 | 卖出 | 卖出 | ||
| 做多 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 买入 | 买入 | ||
3 |
瑞郎篮子 |
|
CHFJPY | USDCHF | GBPCHF | EURCHF | AUDCHF | NZDCHF | CADCHF |
| 做空 | 卖出 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | ||
| 做多 | 买入 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | ||
4 |
欧元篮子 |
|
EURUSD | EURJPY | EURCHF | EURGBP | EURNZD | EURCAD | EURAUD |
| 做空 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | ||
| 做多 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | ||
5 |
英镑篮子 |
|
EURGBP | GBPAUD | GBPCAD | GBPCHF | GBPJPY | GBPNZD | GBPUSD |
| 做空 | 买入 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | ||
| 做多 | 卖出 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | ||
6 |
日元篮子 |
|
AUDJPY | CADJPY | CHFJPY | EURJPY | GBPJPY | NZDJPY | USDJPY |
| 做空 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | 买入 | ||
| 做多 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | 卖出 | ||
7 |
纽元篮子 |
|
NZDUSD | AUDNZD | NZDJPY | NZDCAD | NZDCHF | EURNZD | GBPNZD |
| 做空 | 卖出 | 买入 | 卖出 | 卖出 | 卖出 | 买入 | 买入 | ||
| 做多 | 买入 | 卖出 | 买入 | 买入 | 买入 | 卖出 | 卖出 | ||
8 |
美元篮子 |
|
EURUSD | GBPUSD | AUDUSD | NZDUSD | USDCAD | USDCHF | USDJPY |
| 做空 | 买入 | 买入 | 买入 | 买入 | 卖出 | 卖出 | 卖出 | ||
| 做多 | 卖出 | 卖出 | 卖出 | 卖出 | 买入 | 买入 | 买入 | ||
表 2. 篮子交易操作
篮子货币状态
我们应该如何决定针对一个货币篮子进行交易操作?仅仅根据单一货币对的行为来判断, 对于大尺寸的篮子, 这将是非常困难的事。我们需要更多篮子货币状态参数的技术数据。将我们的注意力集中到来自 GBP 篮子的三个货币对的 RSI 指标图形, 其名为 GBPUSD, GBPJPY 和 GBPCHF。D1 图形是以下显示的图像:
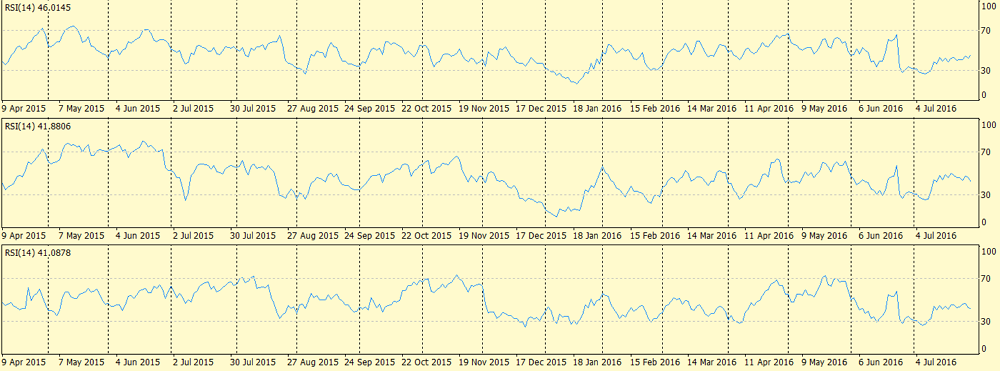
如您所见, 这三幅图有很多共同点: 许多极值位置相似, 而且上下间隔也有很多共同点。这种相似性可以解释为同样的篮子货币 — 英镑。它的坚挺和疲软导致这种上下间隔。
所有三个图形间的差别在很大程度上可解释为货币报价的不同行为。在此情况下, 在 "额外" 局部极值中可看到不同行为的影响, 下降和上升走势的各种梯度, 以及局部方向的变化。
如果我们定义了通用参数 (篮内所有货币对共享) 的行为, 并消除了货币对之间的差别, 我们将实现我们的主要目标 — 参数可视化。在当前的例子中, GBP 超买/超卖状态是通用货币状态参数, 作为 "统一的 RSI" 显示篮子货币的状态, 而非一个货币对。
当然, 我们不可仅用 RSI 来限制自己。也许是基于标准以外的其它类似指标。让我们将它们称为 "统一的指标"。
计算篮子货币状态参数的方法
为了解决这个任务, 我们需要考虑已经存在的, 并尝试类似行动。在这方面首先进入脑海的就是美元指数。正如我们记忆中的, 它显示出美元对比其它六种主要货币的状态。首先, 我们要关注计算方程。这是一个几何平均权重比。我们尝试将此理论应用于我们自定义货币对集合的美元篮子。让我们接受另一个假设 — 去除权重比并减少方程来计算一个正态几何均值。我们所实现的变化将应用于计算几何均值原理, 并在所有篮子上进行计算。在实际实践中, 我们不了解任何货币对的权重比。
让我们来看看, 我们的改变是否有啥影响。为此, 我们使用一个简单的指标:
#property copyright "版权所有 2016, MetaQuotes 软件公司" #property link "http://www.mql5.com" #property version "1.00" #property strict #property indicator_separate_window #property indicator_buffers 1 input int iBarsTotal=300; string pair[]={"EURUSD","GBPUSD","AUDUSD","NZDUSD","USDCAD","USDCHF","USDJPY"}; bool bDirect[]={false,false,false,false,true,true,true}; int iCount=7; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double GetValue(int shift) { double res=1.0,t; for(int i=0; i<iCount; i++) { t=iClose(pair[i],0,shift); if(!bDirect[i]) t=1/t; res*=t; }//结束 for (int i = 0; i < iCount; i++) return (NormalizeDouble(MathPow (res, (double)1/iCount), _Digits) ); } double upp[]; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { IndicatorShortName("testBasket"); IndicatorDigits(_Digits); SetIndexStyle(0,DRAW_LINE,STYLE_SOLID,2,clrGreen); SetIndexBuffer(0,upp); SetIndexLabel(0,"testBasket"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { if(prev_calculated==0) { int total; if(iBarsTotal==0) total=rates_total; else total= MathMin(iBarsTotal,rates_total); for(int i = 0; i<total; i++) upp[i] = GetValue(i); }//结束 if (prev_calculated == 0) else { upp[0]=GetValue(0); } return(rates_total); }
为了比较, 我们使用免费的 USDX.mq4 指标绘制标准方式的美元指数。以下是结果 (H1 时间帧):
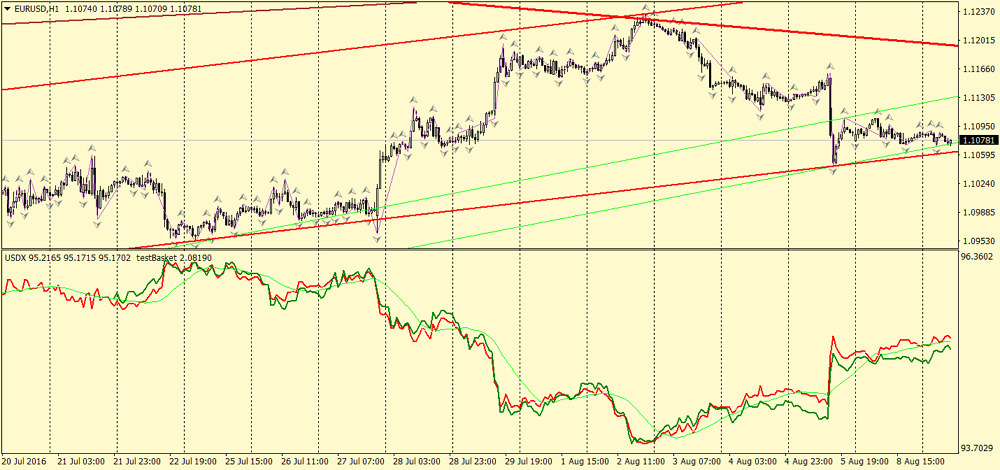
testBasket.mq4 指标在图像里显示为深绿色, 而 USDX.mq4 指标显示为红色和浅绿色 (均线)。我们也许会注意到在 H1 时间帧上完美匹配。走势方向几乎段落吻合, 局部极值点的大多数都如此。
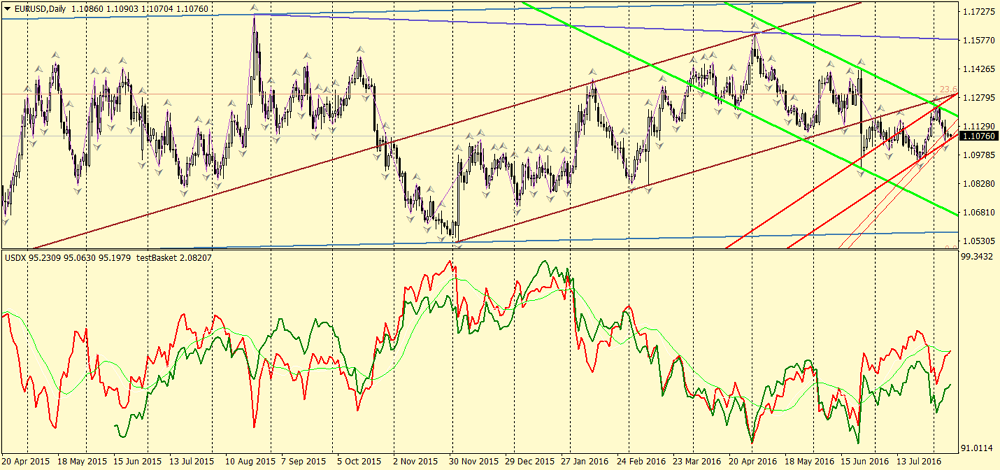
在 D1 时间帧, 图片不太有利, 但依然可接受。大多数局部极值点的位置是相同的, 如同大部分区域的走势方向。在某些区域的差别可轻松解释为缺乏权重比, 以及货币对的集合不同。此外, 彼此相互叠加的图表尺度也是不同的。
在所取得的成果基础上, 我们研究可接受的计算不同篮子货币状态参数几何均值的计算方程。我们将称其为 方法 #1 函数。然而, 我们也应该知道有关方程的限制。更具体而言, 使用它时可取负值参数, 这应是一个馊主意。有相当多的技术指标有这样的参数。此外, 计算几何均值如果不是一个单独的库, 可能要考虑加载到终端。
我们可以应用另一方程, 就是说, 常见的算术平均, 以消除对使用负值作为参数的限制。让我们再基于此方程创建另一个测试指标进行计算。使用随机振荡指标值作为参数:
#property copyright "版权所有 2016, MetaQuotes 软件公司" #property link "http://www.mql5.com" #property version "1.00" #property strict #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 2 input int iBarsTotal=3000; string pair[]={"EURUSD","EURJPY","EURCHF","EURGBP","EURNZD","EURCAD","EURAUD"}; int iCount=7; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GetValue(int shift,double &s1,double &s2) { s1=0; s2=1; for(int i=0; i<iCount; i++) { s1 += iStochastic(pair[i],0,5,3,3,MODE_SMA,0,0,shift); s2 *= iStochastic(pair[i],0,5,3,3,MODE_SMA,0,0,shift); } s1 = NormalizeDouble(s1/iCount, _Digits); s2 = NormalizeDouble(MathPow (s2, (double)1/iCount), _Digits); } double upp[],upp1[]; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { IndicatorShortName("testBasketS"); IndicatorDigits(_Digits); SetIndexStyle(0,DRAW_LINE,STYLE_SOLID,2,clrRed); SetIndexBuffer(0,upp); SetIndexLabel(0,"testBasketSA"); SetIndexStyle(1,DRAW_LINE,STYLE_SOLID,2,clrGreen); SetIndexBuffer(1,upp1); SetIndexLabel(1,"testBasketSG"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { if(prev_calculated==0) { int total; if(iBarsTotal==0) total=rates_total; else total= MathMin(iBarsTotal,rates_total); for(int i = 0; i<total; i++) GetValue(i,upp[i],upp1[i]); }//结束 if (prev_calculated == 0) else { GetValue(0,upp[0],upp1[0]); } return(rates_total); }
指标下载到 EURGBP D1 图表。得到的数值示意如下:
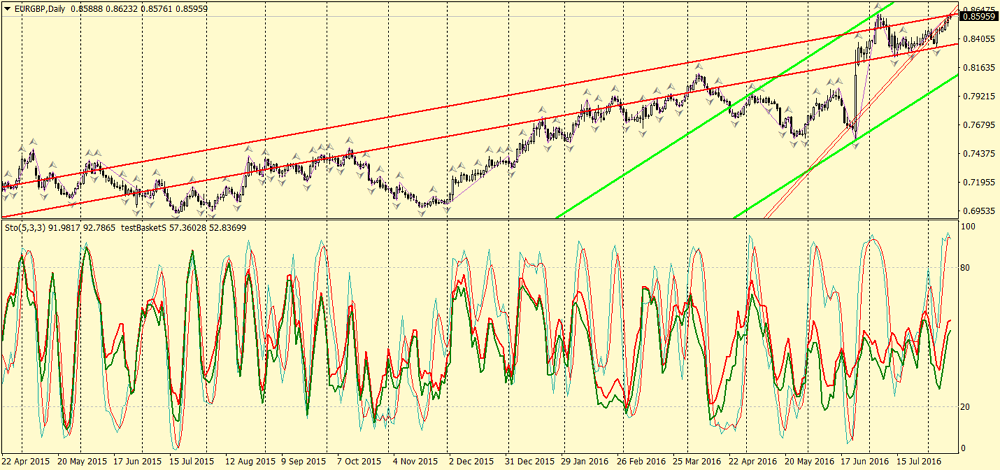
细线代表原始的随机振荡, 红色双实线是基于算术均值方程的新 统一随机振荡, 而绿色双实线表示基于几何均值的比较值。
分析方程, 我们可看到它们产生的结果非常相似。基于几何均值的图形具有较明显的极端点, 而基于算术平均值的那根则更光滑。虽然, 也许这并没什么, 仅是我们的主观印象。负数参数与 PC 计算力相关联的限制似乎是影响实际应用的最关键因素。一般而言, 算术平均值也可以如同 方法 #2 那样应用于计算。
初步的实际结论
读过了之前的段落之后, 您也许会问自己 "这一切的所有需要是什么?" 我们已经得到了绘制类似美元指数图形的新指标, 还有另一个指标可绘制随机振荡风格的图形。我们还得到了另一个指标可绘制类似于标准 RSI 的图表。但是我们已拥有传统的 RSI 和随机振荡。为什么我们还需要其它的呢?让我们来尝试回答这个问题。
- 统一指标提供一篮子货币的状态数据, 允许交易者预测篮子内所有货币对的走势。反过来, 这种预测可用于篮子内所有货币对的交易操作。
- 组合指标形成一个类似常规的 (像是在一幅大图像里包含一个随机振荡) 过滤器, 有助于交易者避免篮内某货币对入场, 分析图形交叉点并检测背离。
- 我们不要忘记两种货币组成一对, 且它们中的每一个都有自己的篮子。交易者可以得到它们当中每一个的数据, 并使用统一指标来规划它们的进一步行动。
所有这些点均可作为开发有效交易系统的基础。此外, 统一指标可与其它交易系统联用。不过, 这个话题已超出这篇介绍性文章的界限。
结论
请记住, 交易决策应基于若干个信号作出, 除非您应用了一个非指标交易方法。本文描述了一个相对新颖的获取信号的方法。然而, 不应考虑用它作为标准方法的完全替代品。统一 RSI, 随机指标和其它指标以及标准指标合并在一起使用, 可以提供足够的高质量确认信号, 从而改善您的交易效率。


