介绍

基本面分析被许多人视为难以理解。目前还不清楚如何抓住要点，以及哪些参数需要取舍。找出影响重大的参数，以及它的时间跨度，不是一件容易的事。

在 2011 年我偶然发现文章 多元还原分析。策略生成器与测试器二合一 并发现其中所描述的方法很有趣。我已经对这个基本分析方法的应用程序进行了研究，并在本文中描述该结果。

什么是“多元还原分析”?

多元还原分析 是从两个或更多自变量估算一个因变量的依赖关系的方法。

那些非数学的思维，也许不会发现这个定义是可理解的。下面的例子将说明这个分析的含义，以及如何使用它。

想象一个研究者打算去估算饮用补充剂时，有规律的体力活动的效率。研究者进行的实验，涉及 24 所大学的学生。学生被分成四个组，每组六人。第一组每天获得 100 毫克补充剂，第二组每天获得 200 毫克，第三组每天获得 300 毫克，第四组每天 400 毫克。这个实验涉及到四个级别的补充剂摄入和三个级别的体力活动。每组的六个人被分成三对。第一组每周锻炼零小时，第二组每周锻炼五小时，第三组每周体力活动十小时。实验结束后每个参与者体重都有所减轻。数据已经输入到以下的表格:

每位参与者减重结果

因此，我们有两个问题:

1. 是什么造成了这种减重 - 补充剂或体力活动？
2. 在体重变化和影响因素之间有什么关系？

它与金融市场的常见情况很类似，是不是？例如, 当货币价格变化, 此时总会问它是受到什么消息影响。如果有经济因素影响价格，那么当此因素变化多端时价格应该如何变化?

多元还原分析以及程序 STATISTICA 帮助回答这些问题。传递或导入包含数据的表格，并在菜单中选择 'Multiple Regression':

图例. 1. 将例样数据导入程序 STATISTICA

选择菜单项之后, 找到按钮 'Variables' 并点击它:

图例. 2. 多元分析参数屏幕

它会弹出一个窗口，选择变量用于分析。它包括两部分: 在左手边我们能选择什么呢, 我们相信, 是一个因变量 (在我们的例子中它是减轻的体重) 并且在右手边, 我们选择哪些可以影响这些变化。

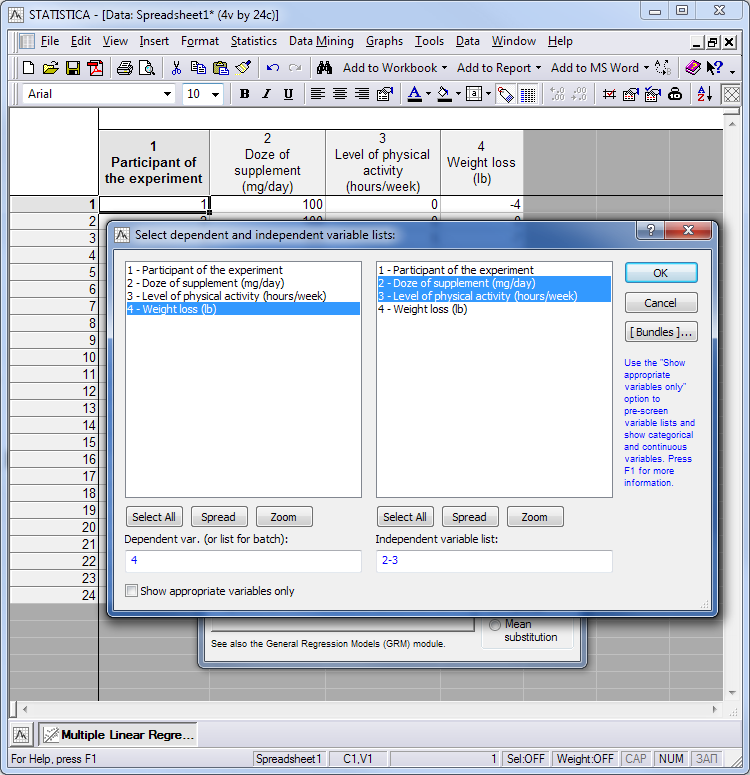
图例. 3. 分配因变量和自变量

按下 'OK' 将我们带回以前的设置对话框窗口，我们必须勾选一个复选框，然后按 'OK':

图例. 4. 为多元分析选择参数

在以下窗口我们选择方法 'All Effects':

图例. 5. 选择方法

在所有的操作之后，我们将得到分析结果的窗口。统计证明影响结果的因素在列表中用红色字体显示（在我们的例子中 'Level of physical activity'）。其它变量:

• 'No. of cases" 是事件分析数量;
• "p" 是相关性的统计有效性级别（级别低于 0.05 被认为是可靠的）;
• "Multiple R" 是方程的因变量与自变量之间的多变量相关性数值。

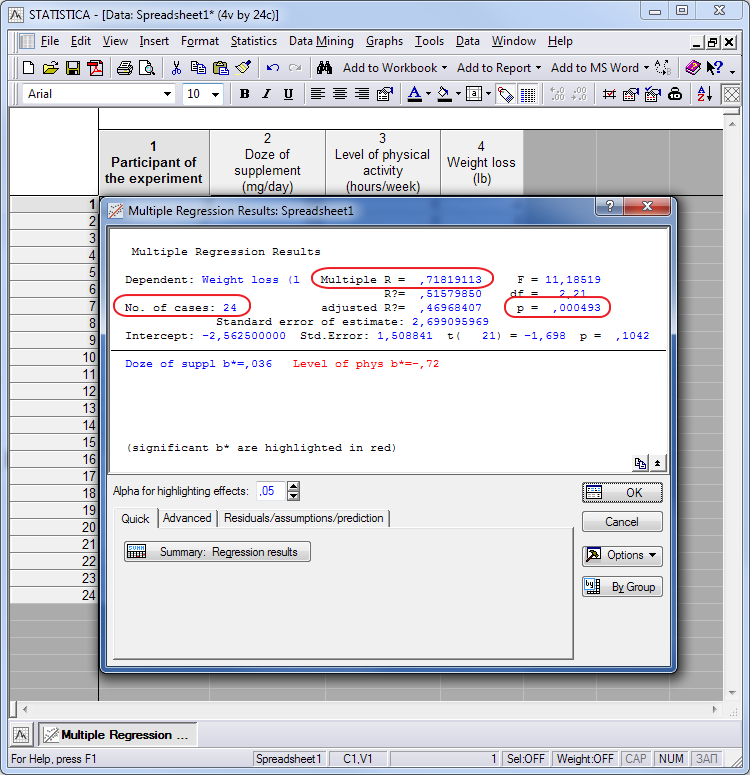
图例. 6. 数据处理结果

数值 'Multiple R= 0,71819113' 可以解释为: 'Multiple R, 减重与其影响因素之间多变量相关性数值, 为 71,82%'。

两个因素之一, 'Level of physical activity', 红色文本。这个因素就是摄取补充剂不足对体重减少的影响。

现在我们仅需通过一个试探性还原方程来计算该因素如何实实在在的影响体重消减的。要做到这一点，按下按钮 'Summary: Regression results' 弹出一个新表格。使用表格中竖列“b”的数值来完成还原方程:

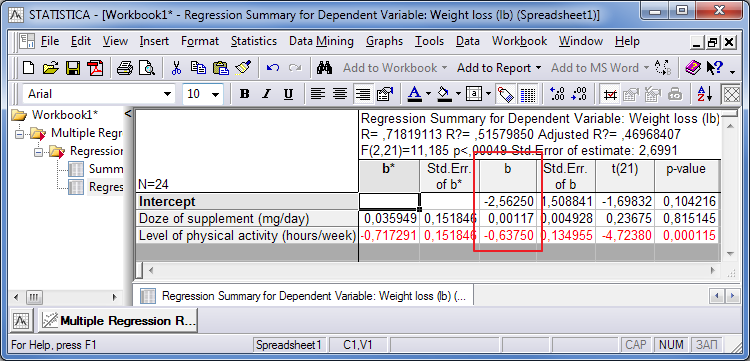
图例. 7. 还原方程变量

我们得到如下方程:

替换方程中数值 (从 STATISTICA 中 Ctrl+C -> 至 Excel 中 Ctrl+V), 我们可以计算出体重变化如何受到补充剂摄取与体力活动强度影响。例如:

• 体重变化 1 = 0.00117*100 - 0.6375*0 - 2.5625 = -2,4455. 这意味着一个人每天服用 100 毫克，不做任何运动，可以失去高达 2.4 磅。
• 体重变化 2 = 0.00117*100 - 0.6375*10 - 2.5625 = -8,8205. 这意味着每天服用 100 毫克补充剂，并且每周运动 10 小时，此时的减重可高达 8.82 磅。

我希望这个例子能澄清多元分析能够做什么的想法。事实上，一些人可能会发现它用于自我检查很有用，比如他们的饮食是否有效，以及他们是否需要去健身房。

现在，我们要将实验获得的想法运用在货币上。让我们假设 EURUSD 货币对的价格变化是因变量，来自热门资源 Forex Factory（外汇工厂） 的事件日历中的宏观经济统计数据是自变量。

与以上例子类似，我们可以通过多元分析找出影响货币价格的宏观因素。我们也可以列出一个方程来估算当宏观经济统计数据发布后货币价格将达到的数值。

准备数据并导入到程序 STATISTICA 中。

当与外汇厂的网站工作时，我遇到了以下问题，我强烈建议考虑一下。在这个资源中，相同的数据以不同的格式发布。例如, 数字也许会是文本格式，或附加的文本数据，导致正常收集数据十分困难。解析网站来收集数据也许会失败。

过去几年，我手工从新闻日历中收集所有 99 个有关美国的因素数值。

图例. 8. 发布的美国宏观经济指数

我以统一格式处理了所有数字，并删除了附加文本如 "million" 和 "billion" 等等，并把所有数据归类到七个纵列（参看本文附件中文件"calendar_usd.zip"），以及添加了 EURUSD D1 周期的报价。

列标题:

• 日期
• 月年
• 时间
• 时区
• 货币
• 描述
• 前值

结果清单有超过 6700 条的宏观经济数据，以及 EURUSD 的报价，对于简单的手工分析这没有实际意义。在独立纵列中按类型排序，并且横行按日期排列后，将所有数据导入表格，这需要一个额外的处理器。我们使用脚本 ListConvertToTable 来处理数据并转换到表格。

在脚本的设置对话窗口，需要命名一个输入文件和一个目标文件。输入文件必须被放置在终端数据目录/MQL5/Files, 输出文件也会在此处创建。

由于有大量的数据，消息列表的处理可能需要相当长的时间。报警内置于脚本，将指明它处于什么阶段。报警 '8' 将令您知道处理结束，您可以使用文件。经过多元分析处理的表格将会附加在本文的文件中。

我得到了如下结果 (参看附件中文件 'calendar_usd_out.zip'):

图例. 9. ListConvertToTable 脚本执行结果

我们将再次使用程序 STATISTICA 来处理数据。为了上载一个 CSV 文件至 STATISTICA, 请按照以下步骤:

• 在 STATISTICA 中打开 'File', 之后 'Open', 选择分拣类型 'Data files' 并打开您的 CSV 文件。
• 在窗口中，文本文件导入类型保留 'Delimited' 并按 'OK'。
• 在打开的窗口中包括下划线项目
• 在字段 'Decimal separator character' 中必须有一个句点，无所谓一个与否:

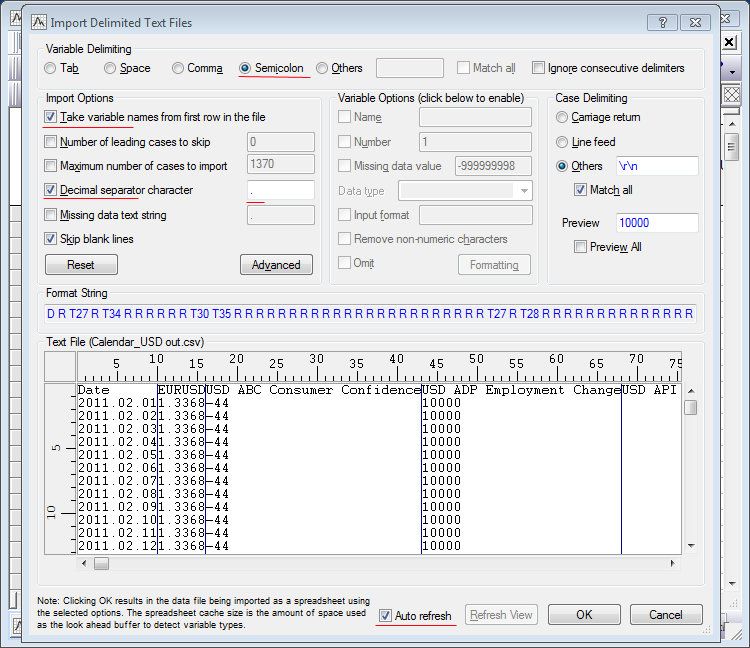
图例. 10. 导入 .csv 格式的表格至程序 STATISTICA

按 'OK'，您将得到带有您的数据的表格。用于多元还原分析的数据已经准备就绪。为了分析数据对以下价格变化的影响，有必要加入价格变化产生的周期。我选择自 2010 以来的消息，并且有三个选项用于分析因变量。

• 消息发布后 1 天的货币价格变化;
• 消息发布后 5 天的货币价格变化;
• 消息发布后 10 天的货币价格变化。

在输出到程序 STATISTICA 之前或在程序窗口中，可以在 CSV 文件中手工添加这些列:

图例. 11. 扩展数据表格

数据准备就绪，从中我们可以看出，影响汇率的原因。

诱发因素对于货币价格有极大影响。

开始还原分析 ('Statistics'->'Multiple Regression')。在分离窗口的选卡 'Advanced' 中启用标记项目。按 'Variables' 按钮。

在第一个字段中，选择因变量，并在第二个字段中选择自变量。我们的方程将依据所选择的变量值:

图例. 12. 用于选择指标的窗口

使用按钮 'Variables'，选择用于分析的数据:

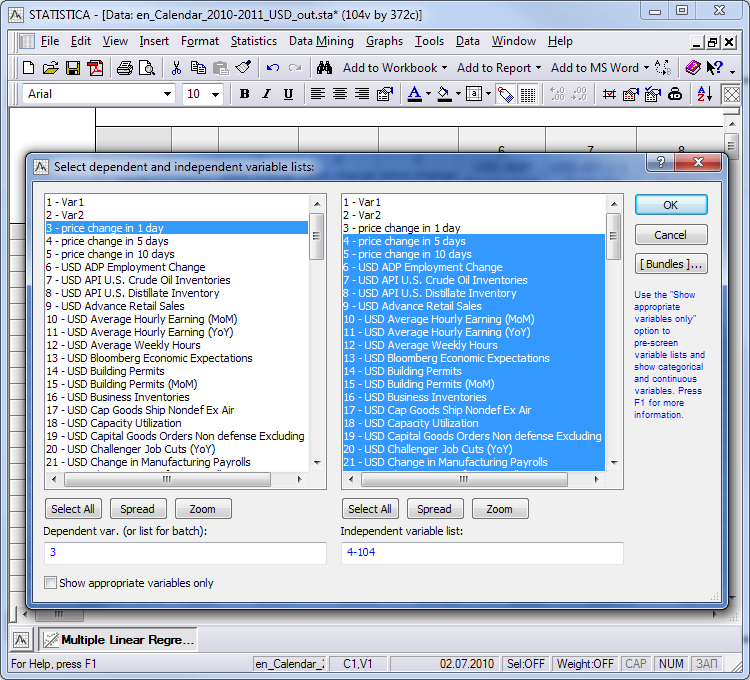
图例. 13. 分配因变量和自变量

一个带有 'Some variables have no variance' 的警告窗口将会出现，它表示一些选择的自变量不能留空。这些列必须要删除。经过排除我们发现第 49 列 'USD Federal Open Market Committee Rate Decision', 删除它并得到用于分析的表格(参看附件中的文件 "calendar_2010-2011_usd_out.zip")。

点击 "OK"。在打开的窗口中，我们在 'Advanced' 选项卡中勾选相应的复选框:

图例. 14. 选择方法 逐级向前

按下按钮 'OK' 完成选项选择。在下一个窗口选择方法 'Forward Stepwise' 启用自动数据选择并再次按下 'OK':

图例. 15. 选择方法 逐级向前

我们都在冲刺阶段。当您在新窗口中看到还原分析成功的消息, 按下按钮 'Summary: Regression results'。

指标自动选择，挑选出那些在自变量和因变量之间对多变量相关性贡献最大的。在我们的案例中，它是对价格影响最大指标的一个集合．自动选择，在本质上，具有策略生成器的作用。生成的方程将只包括那些描述价格行为最可靠方法的指标。

我必须说明的是，用于 STATISTICA 进行分析的指标包含规则，并非一直优化的。举个实例，还原方程可包括大量的非可靠指标（结果表格中黑色字体）。如果列表中包含非可靠指标，那么返回到选择指标的阶段，并从大量指标中剔除非可靠的，用于分析。

在分析结果窗口中返回按下 'Cancel'，并重复分析。尽量通过这种方式排除所有非可靠指标。同时，要记住，得到的多变量相关性数值 (Multiple R)，不应该显著小于初始值。您可以从分析中逐个删除所有非可靠指标，或将它们放在一起。首选第一种方法。

在结束时，只有影响价格波动的可靠指标还留在表中。在该表格中，发现对价格有影响的变量以红色高亮，而影响为零的为黑色。

一旦分析完成，部分指标被发现在它们公布后会对货币价格产生影响。指标集合对于每个周期都不同。在窗口左手边选择 'price change in 1 day' (即，我们分析在指标发布后一天的价格行为) 作为自变量，我们将得到以下:

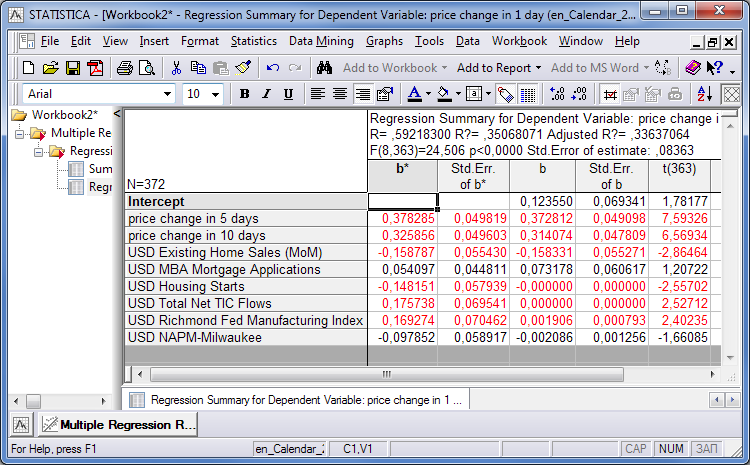
图例. 16. 自变量 'price change in 1 day'

点击 'Cancel' 返回并选择 'Variables' 回到变量选择表单。逐渐地，我们从自变量列表中删除黑色的条目，只留下那些红色的。剩余条目包含的消息将会影响第二天的价格。

请注意表格中的条目颜色不同。自变量对因变量有显著影响，则用红色。在下图中所有条目均为红色，即输入数据之后，方程的错误结果小于第一种情况。影响的级别可通过最后一列的 “p-value”系数来评估(数值越小越好)。那些对价格影响为零的变量可以根据这些系数去除。

选择 'price change in 5 days' 并逐步去除不相关的条目，整理出有意义的消息，我们会得到以下结果:

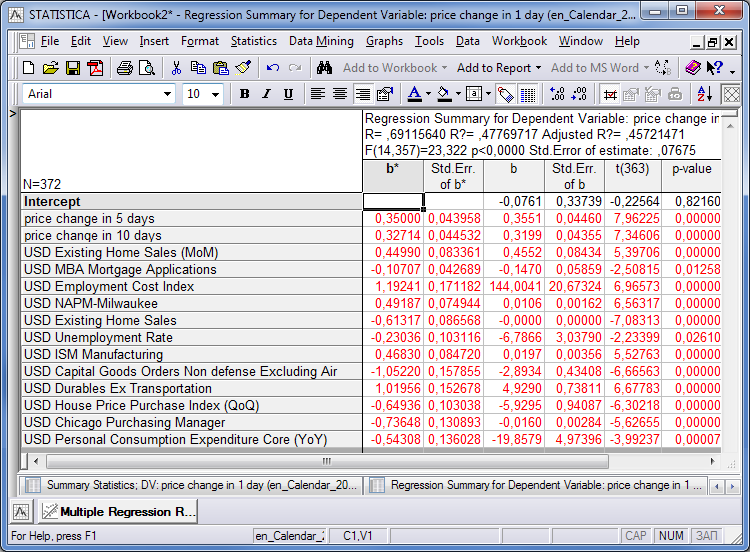
图例. 17. 自变量 'price change in 5 days'

我们最后选择 'price change in 10 days' 作为自变量, 我们将得到:

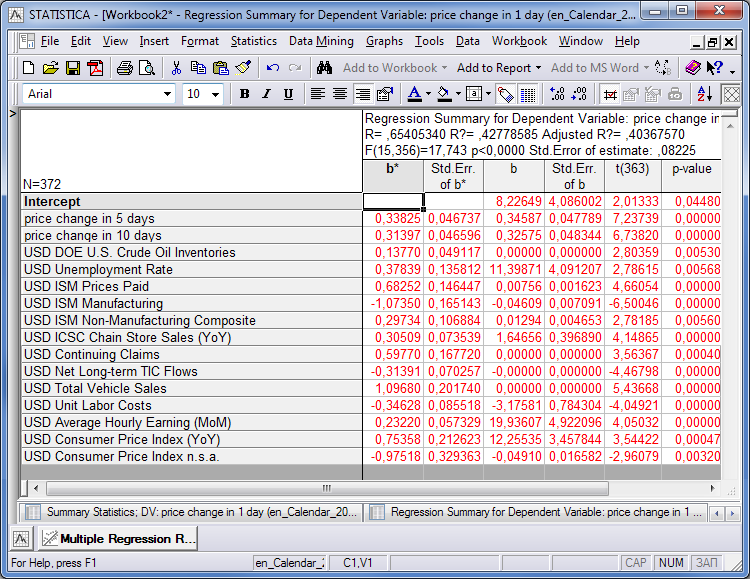
图例. 18. 自变量 'price change in 5 days'

当我们选择一个自变量，在指标数值发布后一天的价格变化，我们可以看到，从 2010 年到 2011 中期，价格大多受到由 Richmond 研究所发布的房地产开发和指数的影响。

数据公布后延伸 5 天，生产和非生产行业指数，劳动力成本和失业率指标加入到发展产业的数据。

当我们考虑 10 天，影响力指数突变。生产和非生产行业指数，房产发展应用，失业率和能源价格的价格走到了前列。

因此，影响 EURUSD 货币对价格的因素，与基本面宏观数据分析十分类似，其重要性在所有的教科书中都会强调。正如我们所看到的，它是由数学和统计学证明的。

还原方程及结果预测

仅知道影响价格的因素还是不够的，重要的是能够估算数据发布后价格如何变化。为此，我们将列一个还原方程，就像这篇文章开头的例子。

我们将基于图例.17 中的表格 'price change in 5 days' 里采集的数值列还原方程。为此，我们将使用的变量来自标题为 'b' 的纵列。第一行是数字常量, 在分析结束时得到的。它的计算将在下文中予以考虑。

让我们根据这些系数列还原方程:

此处我们使用来自“b”栏的值作为系数，并将公布的宏观经济数据作为方括号中的乘数。

在方程中输入发布于源网站上的宏观经济指数的数值, 我们将得到一个数字 R, 大于或小于 0。如果输入新数据的结果大于零，那么就意味着该价格在所述期间增加，选择用于分析。该 R 的数值将表示价格增长。负值 R 意即价格走低。该 R 值在此情况下将表示价格下跌。

将此数值代入上述公式并基于 EURUSD 的例子考虑结果。我们将使用 04.08.2010 的条目数据作为例子，把系数代入方程:

R=-0,0230，因此，接下来的 5 天下跌趋势持续，从 2010 年 4 月 8 日起，价格下降了 -230 点。让我们来看看 EURUSD 货币对在此期间的图表:

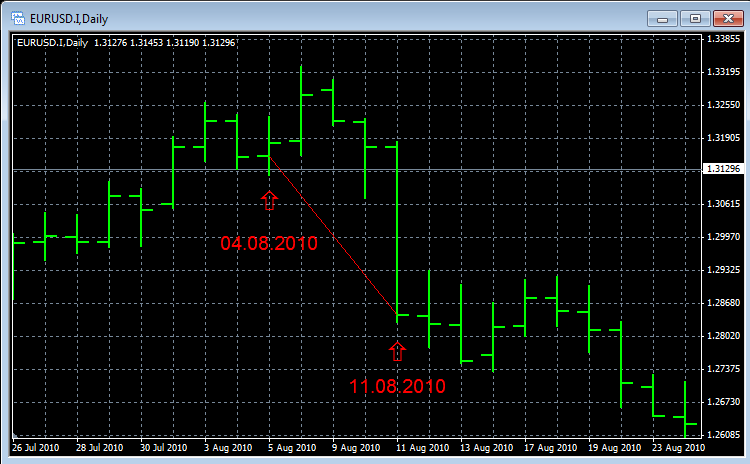
图例. 19. EURUSD 08.2010

正如我们从图表中看到的，预测是准确的，在 5 个交易日，价格从 1.3154 下跌到 1.2844 (收盘于八月十一日)，即 -310 点。基于还原方程的结果预测出的价格下跌被证明。类似地，其它的日期也可以代入。

结论

本文中研究的分析宏观经济数据的方式，可以简化并自动分析基本面，所以即使是新手也能处理好大量的经济数据。

此外，这样的基本面分析方法还提供了一个机会，根据消息即刻反应，并调整交易。

请注意，预测不能视为货币价格将会按照预计方向变化的绝对保证。预测结果只是概率，取决于很多因素。此外，还原方程当有新的数据到达，会被重新计算。

祝您及预测好运！