内容
- 概述
- 应用 Graphics\Graphic.mqh 函数库
- 交换, 比较和边界函数
- 排序方法
- 选择排序
- 插入排序
- 冒泡排序
- 快速排序
- 归并排序
- 堆排序
- 基数排序, 最高位优先和最低位优先
- 其它排序
- 方法速度汇总表
- 所有方法在单一屏幕上
- 多线程测试
- 编者注
概述
在网页上, 您可以找到一些展示各种排序类型的视频。例如, 在此 您能够发现 24 种可视排序算法。我以此视频为基础, 并附有排序算法列表。
Graphic.mqh 函数库以 MQL5 设计, 负责图形处理。它已在许多文章中描述过。例如, 函数库的函数详情展示 在此。我的目标是描述其应用领域, 并详细研究排序过程。这里描述排序的一般概念, 因为每种排序类型至少已经具有一篇单独的论文, 而有些排序类型更是详细研究的对象。
应用 Graphics\Graphic.mqh 函数库
首先, 我们需要包含函数库。
#include <Graphics\Graphic.mqh>
我们将利用 Gswap() 和 GBool() 交换和比较函数来对直方图柱线进行排序。要处理的元素 (比较, 替换等) 以颜色高亮显示。为达此目的, 每个颜色会分配一个单独的 CCurve 类型对象。将它们全局化, 以便无需通过 Gswap 函数 (int i, int j, CGraphic &G, CCurve &A, CCurve &B 和 CCurve &C) 来划分这些对象。CCurve 类没有省缺构造函数, 因此它不能简单地声明为全局。所以, 声明全局 CCurve 类型指针 — *CMain。
颜色可以通过三种不同的方式进行设置。最直观的是 C'0x00,0x00,0xFF' 或 C'Blue, Green, Red'。创建曲线所用的 Graphic 类的 CurveAdd() 已有多种实现。对于主体元素, 可以方便地选择具有单一数值数组的 CurveAdd(arr, CURVE_HISTOGRAM, "Main"), 而对于辅助元素 — 则使用具有参数 X 数组和数值 Y 数组的 CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap"), 因为只有两个元素。将辅助线数组全局化是很方便的。
#include <Graphics\Graphic.mqh> #property script_show_inputs input int N =42; CGraphic Graphic; CCurve *CMain; CCurve *CGreen; CCurve *CBlue; CCurve *CRed; CCurve *CViolet; double X[2],Y[2],XZ[2],YZ[2]; //+------------------------------------------------------------------+ //| 脚本程序开始函数 | //+------------------------------------------------------------------+ void OnStart() { //数组------------------------------ double arr[]; FillArr(arr,N); X[0]=0;X[1]=0; Y[0] =0;Y[1]=0; //------------------------------------- Graphic.Create(0,"G",0,30,30,780,380); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //索引 0 CMain.HistogramWidth(4*50/N); CBlue =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //索引 1 CBlue.Color(C'0xFF,0x00,0x00'); CBlue.HistogramWidth(4*50/N); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //索引 2 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(4*50/N); CGreen =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //索引 3 CGreen.Color(C'0x00,0xFF,0x00'); CGreen.HistogramWidth(4*50/N); CViolet =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //索引 4 CViolet.Color(C'0xFF,0x00,0xFF'); CViolet.HistogramWidth(4*50/N); Graphic.XAxis().Min(-0.5); Graphic.CurvePlot(4); Graphic.CurvePlot(2); Graphic.CurvePlot(0); //Graphic.CurvePlotAll(); 只需显示所有可用的曲线 Graphic.Update(); Sleep(5000); int f =ObjectsDeleteAll(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void FillArr(double &arr[],int num) { int x =ArrayResize(arr,num); for(int i=0;i<num;i++) arr[i]=rand()/328+10; }
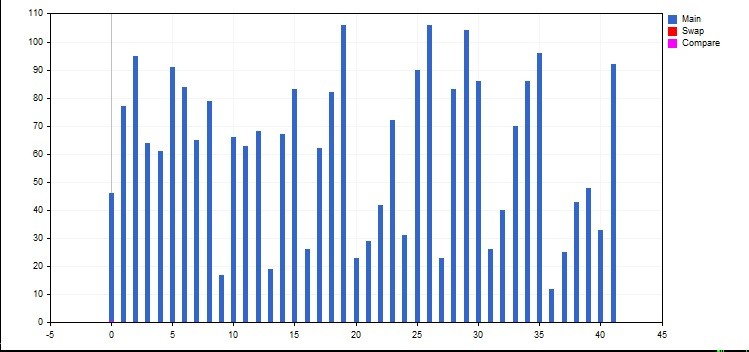
Graphic.XAxis().Min(-5) 设置自 Y 轴的缩进, 以使零元素不与其合并。Histogramwidth() 是柱线宽度。
FillArr() 函数用随机数从 10 (不能与 X 轴合并) 到 110 填充数组。'arr' 数组是局部的, 以便交换函数看上去像标准的 swap(arr, i, j)。最后一条命令 ObjectDeleteAll 会擦除我们已绘制的内容。否则, 我们必须通过菜单的对象列表 Ctrl+B 来删除对象。
我们的准备工作已就绪。现在是时候开始排序了。
交换, 比较和边界函数
我们编写可视化的排序交换、比较和分配边界的函数。第一个交换函数 void Gswap() 是标准的, 尽管它具有用于分配比较元素的 CRed 曲线
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void Gswap(double &arr[],int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CRed.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmS); double sw = arr[i]; arr[i]=arr[j]; arr[j]=sw; //------------------------- Y[0] =0; Y[1] =0; CRed.Update(X,Y); CMain.Update(arr); Graphic.Redraw(); Graphic.Update(); //------------------------- }
首先, 分配列。然后在休眠所定义的演示速度 (TmS) 时间后返回到初始状态。以类似方式编写比较函数 "<" 和 "<=", bool GBool(double arr, int i, int j) 和 GBoolEq(double arr, int i, int j)。将另一种颜色 CVOLE 的柱线加入它们。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool GBool(double &arr[], int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmC); Y[0]=0; Y[1]=0; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); return arr[i]<arr[j]; }
分配边界函数, 其柱线不应该被擦除。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i];YZ[1]=a[j]; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); }
现在, 我们把注意力集中在排序上。
排序方法
在开始分析方法之前, 我建议启动下面附带的 VisualSort 应用程序 (VisualSort.ex5)。它可令您直观地看到每种排序如何分别工作。完整的排序代码位于 GSort.mqh 包含文件中。此文件十分巨大, 所以我在此仅叙述了主要思路。
- 通常, 开始研究的第一个排序是 选择排序。首先, 我们找到当前列表中的最小值的编号, 并将其替换为第一个未排序位置的数值。
template <typename T> void Select(T &arr[]) { int n = ArraySize(arr); for(int j=0;j<n;j++) { int mid=j; for(int i=j+1;i<n;i++) { if(arr[i]<arr[mid]) { mid=i; } } if(arr[j]>arr[mid]){swap(arr,j,mid);} } }
此处和以下的一部分, 交换功能是先前描述的 Gswap(), 而数组元素比较之后被替换则为 GBool()。例如, if(arr[i]<arr[mid]) => if(GBool(arr,i,mid).
- 下一个排序类型 (通常在玩牌时使用) 是 插入排序。在此方法中, 输入序列的元素每次分析一个。每个新到达的元素被放置在之前安排的元素中的适当位置。基本方法:
template<typename T> void Insert(T &arr[]) { int n= ArraySize(arr); for(int i=1;i<n;i++) { int j=i; while(j>0) { if(arr[j]<arr[j-1]) { swap(arr,j,j-1); j--; } else j=0; } } }
此方法的衍生物是希尔排序和 折半插入排序。第一个不仅比较相邻的元素, 而且比较位于一定距离的元素。换言之, 这是初步 "粗略" 处理的插入排序。折半插入利用对半搜索查找插入位置。在上述演示 (VisualSort.ex5) 中, 我们可以清楚地看到, 希尔使用逐渐减少的 "comb" 来搜索数组。在这方面, 它与以下描述的梳子排序有很多共同之处。
- 冒泡排序 及其衍生体 — 鸡尾酒, 地精, 梳子和奇偶排序。冒泡排序背后的思路很简单: 从整个数组的开始到结束比较两个相邻的元素。如果没有排序, 我们交换它们的位置。作为每次迭代的结果, 最大的元素将位于数组的末尾。然后重复该过程。最后, 我们得到一个排序的数组。基本的冒泡排序算法:
template<typename T> void BubbleSort(T &a[]) { int n =ArraySize(a); for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a,j,j+1); swapped = true; } } if (!swapped) break; } }
在鸡尾酒排序中, 从两个方向处理, 允许我们同时检测大、小元素。地精排序很有趣, 它是在一个单一的循环中实现的。我们来看看它的代码:
void GGnomeSort(double &a[]) { int n =ArraySize(a); int i=0; while(i<n) { if(i==0||GBoolEq(a,i-1,i)) i++; //if(i==0||a[i-1]<a[i]) else { Gswap(a,i,i-1); //交换 a[i] 和 a[i-1] i--; } } }
如果我们标记已排序元素的位置, 我们将得到插入排序。梳法使用与希尔相同的思路: 它沿着数组被梳理为不同的步骤。优化缩减因子 = 1.247 ≈ ( 1 / ( 1-е^(-φ) ) ), 此处 е 是指数且 φ 是一个 "黄金" 数字。当应用在小数组时, 梳子和希尔排序在速度方面类似于快速排序方法。奇偶排序轮流处理奇偶元素。由于它已被开发出多线程实现, 所以在我们的例子中未使用。
- 更复杂的方法是基于 "分治" 的原则。标准示例是 霍尔排序或快速排序
算法的整体思路如下: 我们从数组中选择枢轴元素。可以选择任意数组元素作为枢轴。所有其它元素与枢轴进行比较, 并在数组内重新排列, 使得数组被分成两个连续的部分: 比枢轴部分 "小", 枢轴之后是 "超过" 它的值。如果片段长度大于 1, 则对 "小" 和 "超过" 片段递归执行相同的操作顺序。基本思路可以在伪代码中找到:
algorithm quicksort(A, lo, hi) is if (lo < hi) { p = partition(A, lo, hi); quicksort(A, lo, p – 1); quicksort(A, p, hi);}
在这种情况下, 排序选项的差别因数组分区的不同的方式而减少。在原始版本中, 指针从相反一侧向彼此移动。左侧指针找到超过枢轴的元素, 而右侧的指针查找较小的元素, 并将它们互换。在另一个版本中, 两个指针从左到右移动。当第一个指针找到 "较小" 元素时, 它将该元素移动到第二个指针的位置。如果数组包含许多相同的元素, 则为元素分区分配的空间等于枢轴。例如, 当需要仅通过两个键 — "M" (男) 和 "F" (女) 对雇员进行分类时, 就应用这种分配。下面所示适当的分区:
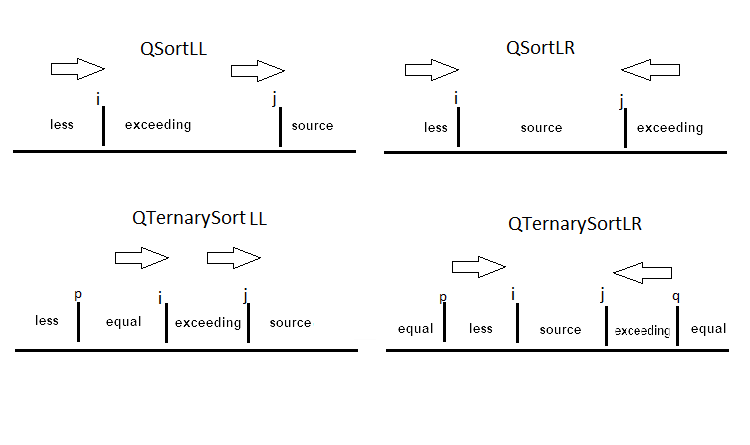
我们以霍尔分区为例来看 QSortLR:
//----------------------QsortLR----------------------------------------+ void GQsortLR(double &arr[],int l,int r) { if(l<r) { GBorders(arr,l,r); int mid =PartitionLR(arr,l,r); GQsortLR(arr,l,mid-1); GQsortLR(arr,mid+1,r); } } int PartitionLR(double &arr[],int l,int r) { int i =l-1; int j =r; for(;;) { while(GBool(arr,++i,r)); j--; while(GBool(arr,r,j)){if(j==l) break;j--;} if(i>=j) break; Gswap(arr,i,j); } //--------------------------------------------- Gswap(arr,i,r); YZ[0]=0;YZ[1]=0; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); return i; }
数组可分为 3, 4, 5, 5 个部分和几个枢轴元素。也可以使用具有两个枢轴元素的 DualPivot 排序。
- 其它基于 "分治" 原则的方法使已排序数组部分的合并。它们划分数组, 直到它的长度等于 1 (已排序), 然后它们应用合并函数, 也可以对元素进行排序。一般原则:
void GMergesort (double &a[], int l, int r) { int m = (r+l)/2; GMergesort(a, l, m); GMergesort(a, m+1, r) ; Merge(a, l, m, r); }
BitonicSort() 令数组的一半升序, 而另一半降序, 之后将它们组合。
- 堆排序
一般原则如下。通过 "筛选" 数组形成 "堆"。删除 "堆" 顶部的旧元素。将其移动到源数组的末尾, 作为最旧的, 将其替换为未排序部分的最后一个元素。构建大小为 n-1 的新 "堆", 等等。"堆" 可以基于不同的原则。例如, Smooth() 排序所应用的 "堆", 元素数量与 Leonardo 数字相等 L(x+2) = L(x+1) +L(x) +1。
- 基数排序。计数排序和基数 MSD/LSD 排序
计数排序是一种 排序算法 应用已排序 数组 的数字范围 (列表) 来计算匹配元素。应用计数排序是合理的, 只有当排序数字的范围与排序集合相比足够小时, 例如, 一百万个小于 1000 的自然数。其原理也适用于基数排序。这是算法:
void CountSort(double &a[]) { int count[]; double aux[]; int k =int(a[int(ArrayMaximum(a))]+1); int n =ArraySize(a); ArrayResize(count,k); ArrayResize(aux,n); for (int i=0;i<k;i++) count[i] = 0; for (int i=0;i<n;i++) count[int(a[i])]++; // 元素编号等于 i for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // 元素编号不大于 i for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // 填充过渡数组 for(int i=0;i<n;i++)a[i]=aux[i]; }
在线性时间内计数排序思想应用于 MSD 和 LSD 排序。这是 N*R 时间, 其中 N 是元素的数量, 而 R 是所选数字系统内的数字表示中的数字数。 MSD (最高有效位) 由顶部数字排序, 而 LSD (最低有效位) — 按照最低。例如, 在折半系统中, LSD 计算在 0 和 1 之间结尾的数字, 将偶数 (0) 分配给前半部分, 而奇数 (1) 到后半部分。MSD, 相反, 从顶部的数字开始。在十进制系统中, 它将小于100 的数字放在开头, 而大于 100 的数字放在后边。然后, 数组再次被分类到片段 0-19, 10-19,..., 100-109 等。此排序方法适用于整数。不过, 报价 1.12307 可以是化整为 1.12307 * 100000。
QuicksortB() 折半快速排序通过组合快速和基数排序获得。QSortLR 排序在此处应用, 尽管选择由顶部数字而不是枢轴数组元素执行。为此, 在 LSD/MSD 中应用搜索第 n 位数字的函数:
int digit(double x,int rdx,int pos) // 此为 x 编号, rdx 数字系统 { // 在我们的案例 2 中, pos 是数字索引 int mid =int(x/pow(rdx,pos)); return mid%rdx; }首先, 通过顶部数字执行排序 int d =int(log(a[ArrayMaximum(a)])/log(2)), 之后部分用递归进行低位数排序。从观感上, 它看起来类似于 QuickSortLR。
- 一些特别的排序
环形排序 适用于数据覆盖导致资源磨损的系统。因此, 此处的任务是找到最少交换量 (Gswap) 的排序。环形排序恰好适用于此。粗略地说, 1 被重新排列至 3, 3 至 2, 2 至 1。每个元素重新排列 0 或 1 次。所有这些要花费很多时间: O(n^2)。这个思路和方法的细节可以在 此处 找到。
臭皮匠排序。这是另一个牵强且 十分低速的排序 示例。算法如下。如果列表末尾的元素值小于开头的元素值, 那么它们应该交换它们的位置。如果列表的当前子集包含 3 个或更多元素, 则: 对于列表的前 2/3 递归调用 Stoodge(), 最后 2/3 递归调用 Stoodge(), 再次针对前 2/3 递归调用 Stoodge(), 等等。
方法速度汇总表
| 排序方法 | 平均时间 |
|---|---|
| 选择排序 | O(n^2) |
| 插入排序 | O(n^2) |
| 折半选择排序 | O(n^2) |
| 希尔排序 | O(n*log(n)) |
| 冒泡排序 | O(n^2) |
| 鸡尾酒排序 | O(n^2) |
| 地精排序 | O(n^2) |
| 梳子排序 | O(n*log(n)) |
| 归并排序 | O(n*log(n)) |
| 双调排序 | O(n*log(n)) |
| 堆排序 | O(n*log(n)) |
| 平滑排序 | O(n*log(n)) |
| 快速排序 LR | O(n*log(n)) |
| 快速排序 LL | O(n*log(n)) |
| 快速排序 (三元, LR) | O(n*log(n)) |
| 快速排序 (三元, LL) | O(n*log(n)) |
| 快速排序 (双枢轴) | O(n*log(n)) |
| 计数排序 | O(n+k) |
| 基数 LSD | O(n*k) |
| 基数 MSD | O(n*k) |
| 快速折半排序 | O(n*log(n)) |
| 环形排序 | O(n^2) |
| 臭皮匠排序 | O(n^2.7) |
所有方法在单一屏幕上
我们在一个屏幕上同时绘制所有描述过的排序。在 原视频 当中, 曾描述过的排序逐一启动。最终结果之后在视频编辑器中编辑。交易平台没有内置的视频编辑功能。这有几个解决方案。
选项 1
模拟多线程。并行排序, 以便在每次比较和交换将队列移交给其它排序之后可以退出函数, 然后在同一个位置重新进入。不含有令任务复杂化的 GOTO 操作符。例如, 这是一开始就描述的最简单的选择排序, 在此情况下的观感如何:
void CSelect(double &arr[]) { static bool ch; static int i,j,mid; int n =ArraySize(arr); switch(mark) { case 0: j=0; mid=j; i=j+1; ch =arr[i]<arr[mid]; if(ch) mid =i; mark =1; return; break; case 1: for(i++;i<n;i++) { ch =arr[i]<arr[mid]; mark =1; if(ch) mid=i; return; } ch =arr[j]>arr[mid]; mark=2; return; break; case 2: if(ch) { swap(arr,j,mid); mark=3; return; } for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark =2; return; } break; case 3: for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark=2; return; } break; } mark=10; }
这一解决方案是相当可行的。如此启动时, 数组已被排序:
while(mark !=10) { CSelectSort(arr); count++; }
'count' 变量显示比较和交换的总数。与此同时, 代码已经变大三到四倍, 这是最简单的排序。还有一些由几个函数组成的递归函数, 等等。
选项 2
有一个更简单的解决方案。MQL5 终端支持多线程的概念。要实现它, 应针对每种排序调用自定义指标。指标应属于每个线程的 单独货币对。市场观察窗口应该有每种排序的足够工具。
n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);
在此, SymbolName (n,0) 是单独工具, 作为参数传递给每个创建的指标。可以通过 SymbolName (n,0) 方便地为图形对象分配名称。一张图表只能有一个具有给定名称的 Graphic 类对象。排序方法, 数组中的元素数量和图形本身的大小不会在此显示。
与视觉显示相关的排序函数选择和其它附加操作 (例如, 将排序名称添加坐标轴) 会在指标本身中进行。
switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");Select(arr); break; case 1: Graphic.XAxis().Name("Insertion"); CMain.Name("Insertion");Insert(arr);break; 等等............................................. }
图形对象的创建需要花费一定的时间。因此, 已经添加了全局变量以便同时进行排序。NAME 是一个全局变量, 金融工具名称的初始值为 0。创建所有必需的对象之后, 值为 1, 而排序完成后所分配值为 2。以这种方式, 您可以跟踪排序的开始和结束。为此, 在 EA 中启动定时器:
void OnTimer() { double x =1.0; double y=0.0; static int start =0; for(int i=0;i<4;i++) { string str; str = SymbolName(i,0); x =x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } if(x&&start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } if(y==8) {PlaySound("success.wav"); EventKillTimer();} }
此处变量 х 捕获开始时间, 而 у — 处理结束时间。
在处理开始时, 播放来自原始视频中的 声音。要播放源文件, 它应该与其它 *.wav 系统声音一样位于 MetaTrader/Sound 文件夹中。如果它位于其它什么位置, 请指定 MQL5 文件夹的路径。最后, 使用 success.wav 文件。
那么, 我们来创建 EA 及以下类型的指标。EA:
enum SortMethod { Selection, Insertion, ..........排序方法......... }; input int Xscale =475; //图表尺度 input int N=64; //元素数量 input SortMethod Sort1; //方法 ..........各种输入................. int OnInit() { //--- 设置全局变量, 启动定时器等。 for(int i=0;i<4;i++) { SymbolSelect(SymbolName(i,0),1); GlobalVariableSet(SymbolName(i,0),0);} ChartSetInteger(0,CHART_SHOW,0); EventSetTimer(1); GlobalVariableSet("ALL",0); //.......................为每种排序打开单独的指标......... x=0*Xscale-Xscale*2*(0/2);//row with the length of 2 y=(0/2)*Yscale+1; SymbolSelect(SymbolName(0,0),1); // 没有它, 一些金融工具可能会发生错误 S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N); return(0); } //+------------------------------------------------------------------+ //| 智能程序逆初函数 | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ChartSetInteger(0,CHART_SHOW,1); EventKillTimer(); int i =ObjectsDeleteAll(0); PlaySound("ok.wav"); GlobalVariableSet("ALL",0); IndicatorRelease(Sort1); .......所有这些都被删除...... //+------------------------------------------------------------------+ //| 智能程序即时报价函数 | //+------------------------------------------------------------------+ void OnTick() { ...空... } //+------------------------------------------------------------------+ void OnTimer() { ....已在上面描述过.... }
相应的 指标:
#include <GSort.mqh> //包含所有之前编写的排序 //+------------------------------------------------------------------+ //| 自定义指标初始化函数 | //+------------------------------------------------------------------+ ..........输入模块..................................... input int SortName; //方法 int N=30; //数字 ...................................................................... int OnInit() { double arr[]; FillArr(arr,N); //用随机数填充数组 GlobalVariableSet(NAME,0); //设置全局变量 Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2); //NAME — 货币对 Graphic.IndentLeft(-30); Graphic.HistoryNameWidth(0); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //索引 0 CMain.HistogramWidth(2); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //索引 1 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(width); ......各种图形参数.......................... Graphic.CurvePlotAll(); Graphic.Update(); GlobalVariableSet(NAME,1); while(!GlobalVariableGet("ALL")); //等待直到所有图形对象被创建 switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");GSelect(arr); break; .....排序列表.............................................. } GlobalVariableSet(NAME,2); return INIT_SUCCEEDED; } //+------------------------------------------------------------------+ //| 自定义指标迭代函数 | //+------------------------------------------------------------------+ int OnCalculate(...) { ..............空........................ } //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Graphic.Destroy(); delete CMain; delete CRed; delete CViolet; delete CGreen; ObjectDelete(0,NAME); }
多线程测试
Light.ex5 和 Sort24.ex5 是现成的程序。它们已经通过资源被复制, 也不需要任何其它东西。当使用源代码时, 应将其安装在相应的指标和声音文件夹中。
Sort24.ex5 带有 24 种排序, 在我的普通单核电脑上 不太稳定且工作时不均衡。因此, 我应该关闭所有不必要的程序, 且不触任何东西。每种排序包含五个图形对象 — 四条曲线和一块画布。所有这些都不断重绘。在 24 个线程中创建 120(!) 个不间断变化的图形对象。这只是一个演示。我尚未令它工作更多。
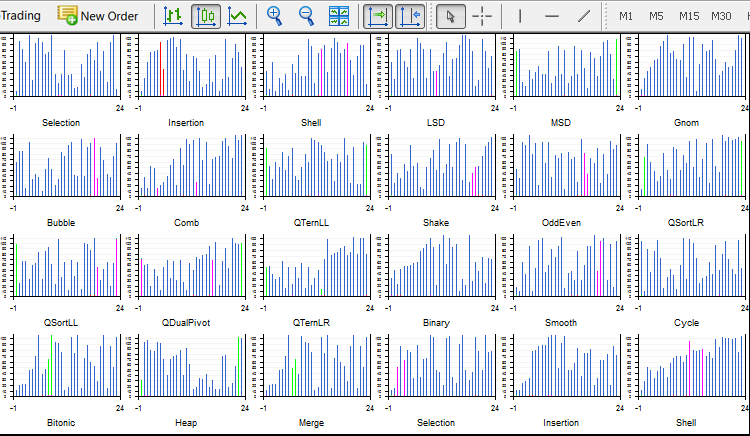
Light.ex5 相当稳定的运行版本同时显示 4 种排序。在此您可以选择每个窗口中的元素数量和排序方法。此外, 可以选择数组洗牌的方法: 随机, 向上 (已排序), 向下 (以相反顺序排序) 和含有许多相同元素 (步数组) 的数组。例如, 快速排序在数组上反向排序降级到 O(n^2), 而堆排序总是排序 n*log(n)。不幸的是, 指标中不支持 Sleep() 函数, 因此速度只取决于系统。此外, 为每个线程分配的资源量也是任意的。如果在每个窗口中启动相同的排序, 它们会以不同的方式完成。
小结
- 单线程 VisualSort 可以 100% 工作
- 四线程 Light 很稳定
- 二十四线程 Sort24 不稳定
我们可以遵照第一个选项模拟多线程。在这种情况下, 我们将能够控制进程。Sleep() 函数将会工作, 每个排序将接收严格相等的时间, 等等。但是, 在这种情况下, 将会舍弃 MQL5 多线程编程的概念。
最终版本:
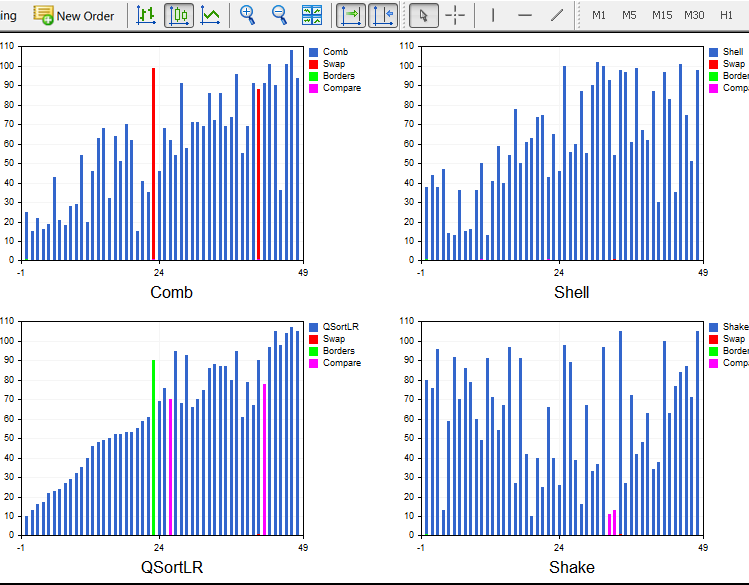
....................................................................................................................................................................
附件文件清单
- VisaulSort.ex5 - 每种排序独立呈现
- Programs(Sort24.ex5, Light.ex5) - 现成的应用程序
- 声音文件
- 代码。程序源代码 - 排序, 指标, 包含文件, EA 等。
编者注
文章的作者利用同时启动多个指标实现了一个有趣的多线程排序版本。这个架构令 PC 的负载大大加剧, 所以我们稍微修改了作者的源代码, 即:
- 禁用从 auxiliary.mq 文件的每个指标中调用图表重绘
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i]+2;YZ[1]=a[j]+5; CGreen.Update(XZ,YZ); Graphic.Redraw(false); Graphic.Update(false); }
- 添加了 randomize() 函数, 为数组中的所有指标准备相同的随机数据
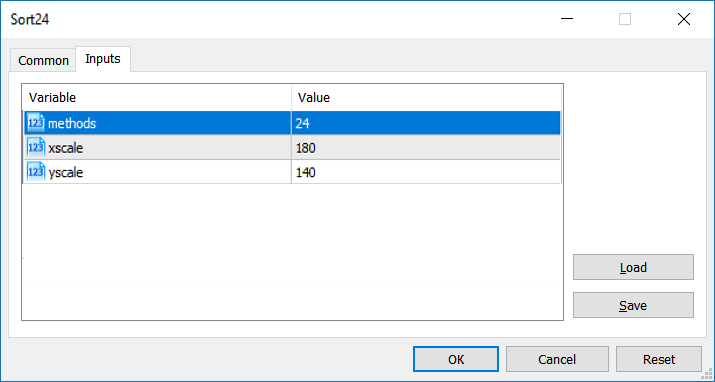
- 将外部参数添加到 IndSort2.mq5 文件中, 用于使用随机值定义数组大小 (在作者版本中它已严格等于24) 和数据生成的初始化 'si' 数
input uint sid=0; //初始化随机数 int N=64; //直方图上的柱条数量
- 将调用 ChartRedraw() 重绘图表的定时器加入到 Sort24.mq5 文件
//+------------------------------------------------------------------+ //| 定时器函数 | //+------------------------------------------------------------------+ void OnTimer() { double x=1.0; double y=0.0; static int start=0; //--- 在循环里检查每个指标的初始化标志 for(int i=0;i<methods;i++) { string str; str=SymbolName(i,0); x=x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } //--- 所有指标成功初始化 if(x && start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } //--- 所有排序完成 if(y==methods*2) { PlaySound("success.wav"); EventKillTimer(); } //--- 更新排序图表 ChartRedraw(); }
- 将音频文件移动到 <>\MQL5\Sounds 文件夹, 以便包含它们作为资源
#resource "\\Sounds\\Sort.wav"; #resource "\\Sounds\\success.wav"; #resource "\\Indicators\\Sort\\IndSort2.ex5"
编译就绪的结构附加在 moderators_edition.zip 存档里。简单地将其打包并复制到您的终端。如果您的电脑不够强大, 建议您在输入中设置 methods=6 或 methods=12。