在 mql5.com 网站上有一些探讨 Kohonen 神经网络主题的文章,例如 在 MetaTrader 5 中使用自组织特征映像(Kohonen 映像) 和 自组织特征映射(Kohonen 映像)- 重访主题。 它们向读者介绍了构建此类神经网络的一般原则,并运用这些映像直观地分析众多财经市场。
然而,实际上,用于算法交易的 Kohonen 网络仅限于一种方法,亦即如同 EA 优化结果所构建的拓扑映像的直观分析。 在此情况下,某个人的价值判断,或者更确切地说,某个人从一张图片中得出合理结论的眼光和能力,或许是关键因素,有关表述数据的附带网络属性,就像螺栓和螺栓问题。
换言之,神经网络算法的特征并未完全使用,即,它们在使用时不会自动提取知识或支持特别推荐的决策。 在本文中,我们所研究的问题是遵照更加正规的方式定义机器人的最佳参数集合。 此外,我们会应用 Kohonen 网络来预测财经范围。 但是,在继续处理这些已有问题之前,我们应该修改现有的源代码,修复一些内容,并进行一些改进。
如果您不熟悉“网络”,“层”,“神经元”(“节点”),“链接”,“权重”,“学习率”,“学习范围”等术语,以及与 Kohonen 网络相关的其他概念,那么强烈建议您首先阅读上述文章。 我们应在这个问题上自我充实,因为若是重新教授这些基本概念会显著令发表文章冗长。
我们将调用在上述文章中前面部分发表的 CSOM 和 CSOMNode 类,并着眼于后者的补充。 其中的关键代码片段实际上是相同的,且继承了相同的问题。
首先,应当注意的是,出于某种原因,上述类中的神经元已进行索引,即通过像素坐标作为构造函数参数来识别和定义。 这不太合乎逻辑,并且在某些方面令计算和调试复杂化。 特别是在此方法下,表述设定会影响计算。 试想一下:有两个完全相似的网络,其格子大小相同,它们正在使用相同的数据集,相同的设定和随机数据生成器初始化进行学习。 然而,获得的结果是不同的,恰恰是因为一个网络的图像大于另一个网络。 这是个错误。
我们将通过数字来检索神经元:在数组 m_node(CSOM 类)中的每个神经元,其坐标 x 和 y 分别对应于 Kohonen 网络输出层中的列号和行号。 每个神经元将采用 CSOMNode::InitNode(x, y) 方法替代 CSOMNode::InitNode(x1, y1, x2, y2) 方法进行初始化。 当我们进行可视化时,以像素为单位更改映像大小,神经元坐标将保持不变。
在继承的源代码中,未使用输入数据常规化。 不过,在输入矢量的不同分量(特征)有不同数值范围的情况下,它会非常重要。 这是 EA 的优化结果,并汇集不同指标数据的情况。 至于优化结果,我们可以看到,有数十万的总利润其数值较小,例如锋锐比率的分数,或恢复因子的一位数值。
您不应该使用这种不同规模的数据来教育 Kohonen 网络,因为网络实际上只考虑较大的分量而忽略较小的分量。 您可以在下面的图像中看到这一点,此图利用我们在本文中逐步深入研究的程序获得,该程序附加在文章末尾。 该程序允许生成随机输入矢量,其中三个分量分别定义在 [0, 1000],[0,1] 和 [-1, +1] 范围内。 特殊输入 UseNormalization 允许启用/禁用常规化。
我们来看看 Kohonen 网络的最终结构,它处在与矢量三维相关的三个平面上。 首先,网络学习结果未经常规化。

Kohonen 网络学习结果未经输入常规化
现在,同例经过常规化。
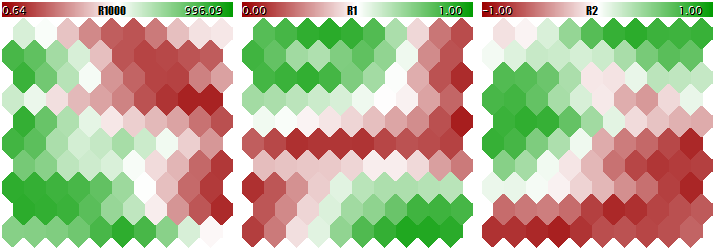
Kohonen 网络输入常规化的学习结果
神经元权重适应程度与颜色梯度成比例。 显然,在非常规化条件下,网络仅在第一平面中学习拓扑分区(分类),而第二和第三分量则被微小噪音充满。 也就是说,网络的分析能力已经实现了三分之一。 启用常规化后,空间排列在所有三个平面中都可见。
许多常规化方法是已知的,但最常用的一种,可能是从每个分量中减去整个选择的平均值,然后将其除以标准偏差,即西格玛或均方根。 这会将变换数据的平均值设置为零,标准偏差设置为一体。
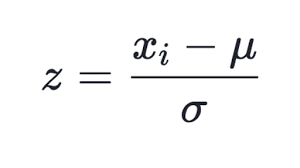 (1)
(1)
更新后的 CSOM 类,方法 Normalize 中采用了此技术。 很明显,您应该首先计算输入数据集的每个分量的平均值和西格玛值,这在方法 InitNormalization 中完成(见下文)。
通过两次运行算法计算平均值和标准偏差的典型公式:应首先找到平均值,然后将其用于计算西格玛值。
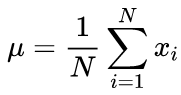 (2)
(2)
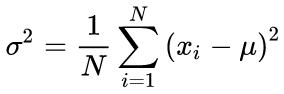 (3)
(3)
在我们的源代码中,我们的单次运行算法基于以下公式:
 (4)
(4)
显然,入口处的常规化需要一个逆反操作 — 逆常规化 — 在出口处,即,将网络的输出值变换到实际数值的范围。 这是通过方法 CSOM::Denormalize 完成的。
由于常规化的数值在零附近对称下降,我们将在开始教育网络之前改变神经元权重的初始化原则 — 替代范围 [0, 1],现在是范围 [-1, +1](参见方法 CSOMNode::InitNode)。 这将提高网络学习的效率。
另一个要修正的方面是学习迭代的计次。 在源类中,迭代应理解为给网络指定每次单独的输入矢量。 因此,应依据教育选择的规模来修正迭代次数。 回想一下,Kohonen 网络学习和信息融合原则假设每个样本都会指定给网络很多次。 例如,如果选择中有 100 个入口,那么迭代次数若要等于 10000 则必须每个入口平均指定 100 次。 但是,如果选择生成 1000 个入口,则迭代次数必须为变 100000。 更便利和传统的方法是定义所谓的“学习时期”的次数,即,所有样本被随机地投喂到网络的每个周期中。 次数将在参数 EpochNumber 中设置。 由于引入它,学习持续时间在参数上与数据集的大小分离。
这一点尤为重要,因为总输入集可以分为两个部分:教育的选择,和所谓的验证选择。 后者用于跟踪网络学习质量。 问题在于教育期间,令网络适配输入有一个“翻面”:网络开始适配特定样本的特征,这样做,丧失了对未知数据进行概括和充分处理的能力(除了用于教育)。 归根结底,学习的理念通常是为了在未来利用网络检测特征的能力。
在所研究的程序中,输入参数 ValidationSetPercent 负责启用验证。 默认情况下,它等于 0,并且所有数据都用于学习。 如果我们指定为 10,那么只有 90% 的样本用于学习,而对于剩余的 10%,在每次迭代(时期)上计算常规化均方差,并且在误差开始增长的时刻,停止学习过程 。
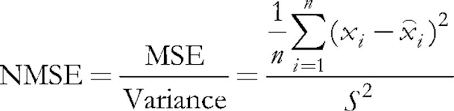 (5)
(5)
常规化包括将均方差除以数据本身的离散度,这导致索引始终低于 1。 当分别考虑每个矢量时,这个均方差实际上是量化误差,因为它是基于其分量和相关神经元突触的权重之间的差值,在所有神经元中给出了这个矢量的最佳近似值。 我们应该记得,这个获胜神经元在 Kohonen 网络中被称为 BMU(最佳匹配单元)或 BMN(最佳匹配节点)— 在 CSOM 类中,GetBestMatchingNode 方法和类似技术负责搜索它。
启用验证后,迭代次数将超过参数 EpochNumber中 指定的次数。 由于 Kohonen 网络架构的特性,只有在网络通过了 EpochNumber 时期上的自组织阶段后,才能执行验证。 在该阶段完成时,学习速率和范围显著降低,以至开始权重的微调,然后收敛阶段开始。 在这里,使用验证集来进行学习的“早期停止”。
是否使用验证取决于问题的特殊性。 此外,验证集可用于匹配网络规模。 出于本文的目的,我们不打算讨论这个问题。 我们只是运用著名的经验规则,将网络规模与教育数据的次数联系起来:
N ~ 5 * sqrt(M) (6)
其中 N 是网络中神经元的数量,M 是输入矢量的数量。 对于具有正方形输出层的 Kohonen 网络,我们得到大小:
S = sqrt(5 * sqrt(M)) (7)
其中 S 是垂直和水平的神经元数量。 我们将这个数值引入参数 CellsX 和 CellsY。
原始源代码中要修正的最后一个问题与处理六边形网格有关。 已知 Kohonen 映像由矩形或六边形的细胞(神经元)布局来构建,并且在源代码中两种模式最初都已实现。 然而,六边形网格仅显示为六边形细胞,但计算时则完全作为矩形网格。 若要在此处找到误差的根源,我们来研究下面的示意图。
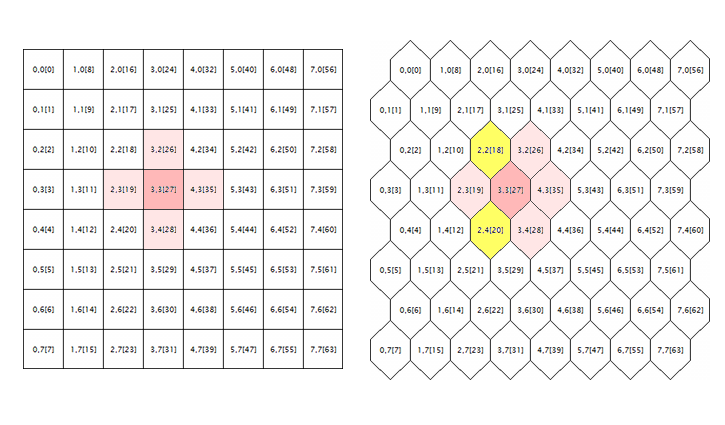
神经元邻域几何:矩形和六边形网格
此处展示了两个几何网格的随机神经元围绕逻辑(在本例中,坐标为 3;3)。 围绕半径为 1。 在正方形网格中,神经元有 4 个直接邻域,而在六边形网格中有 6 个。 把每个细胞外围交替移动半个细胞来实现细化外观。 不过,这并没有改变它们的内部坐标,并且就算法而言,六边形网格中围绕的神经元像以前一样显现 — 它以粉红色标记。
显然,这是错误的,应该通过包含以黄色高亮显示的神经元来修正。
从形式上讲,该算法是根据细胞坐标之间的距离,利用相邻邻域和作为凸减径向函数来计算周边的。 换言之,邻域不是神经元的二元属性(相邻与否),而是由高斯公式计算的连续数量:
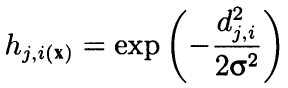 (8)
(8)
此处,d ji 是神经元 j 和 i 之间的距离(连续编号是均值,而非坐标 x 和 y); 且西格玛值是邻域的有效宽度或学习期间逐渐递减的学习半径。 在学习开始时,用对称的“钟”覆盖邻域会比紧密相邻的神经元拥有更大的空间。
由于这个公式取决于距离,它也会扭曲邻域,这是因坐标没有被正确修正。 所以,以下源代码来自 CSOM::Train 方法:
for(int i = 0; i < total_nodes; i++) { double DistToNodeSqr = (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) * (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) + (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y()) * (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y());
已得到补充:
bool odd = ((winningnode % m_ycells) % 2) == 1; for(int i = 0; i < total_nodes; i++) { bool odd_i = ((i % m_ycells) % 2) == 1; double shiftx = 0; if(m_hexCells && odd != odd_i) { if(odd && !odd_i) { shiftx = +0.5; } else // 反之亦然 (!odd && odd_i) { shiftx = -0.5; } } double DistToNodeSqr = (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) * (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) + (m_node[winningnode].GetY() - m_node[i].GetY()) * (m_node[winningnode].GetY() - m_node[i].GetY());
修正 'shiftx' 的方向取决于两个神经元的所在行为偶数或奇数的比率,在这两个神经元之间计算距离。 如果神经元处于同等水平的行中,则无需修正。 如果获胜的神经元处于奇数行,那么偶数行看起来从它向右移动半个细胞,因此,shiftx 等于 +0.5。 如果获胜的神经元处于偶数行,则奇数行显示为向左移动半个细胞,因此,shiftx 等于 -0.5。
现在,尤为重要的是注意以下原始字符串:
if(DistToNodeSqr < WS) { double influence = MathExp(-DistToNodeSqr / (2 * WS)); m_node[i].AdjustWeights(data, learning_rate, influence); }
事实上,这个条件运算符可以确保计算得到一些加速,因为忽略了一个超出西格玛邻域的神经元。 然而,就学习质量而言,高斯公式是理想的,并且这种干预是不合理的。 如果太远的神经元应该被忽略,那么应该是三个西格玛,而不仅仅是一个。 在我们修正了六边形网格的计算之后,更为关键的是,由于位于相邻行中的相邻神经元之间的距离等于 sqrt(1*1 + 0.5*0.5) = 1.118,即高于 1。 在附带的源代码中,此条件运算符被加以注释。 如果您确实需要加速计算,请使用选项:
if(DistToNodeSqr < 9 * WS)
注意! 由于上述细微差别,相邻神经元之间的距离取决于它们的排列(单行距离为 1,而相邻行距离为 1.118),目前的实现仍然不理想,并建议进一步修正以实现完全各向异性。
尽管 Kohonen 网络主要与可视图形映像相关联,但它们的拓扑和学习算法可以在没有任何用户界面的情况下完美地工作。 特别是,预测或压缩信息的问题无须任何可视分析,并且图像的分类可以将结果作为数字传递,即, 一个类的编号或一个事件的概率。 因此,Kohonen 网络的功能分为两个类。 在 CSOM 类中,仅保留了计算,数据加载和存储以及网络加载和存储。 除此之外,还创建了 CSOMDisplay 的派生类,其中放置了所有图形。 在我看来,这是个比第 2 篇文献中提议的更简单、更合理的层次结构。 将来,我们将使用 CSOMDisplay 来解决选择最佳 EA 参数的问题,而 CSOM 将用于预测。
应该注意的是网格类型的特征,即 ,无论是矩形还是六边形,都属于基本类,因为它影响距离的计算。 除了垂直和水平方向上的节点数量,以及数据输入空间的维度外,网格类型是体系结构的一部分,应保存在文件中。 从文件加载网络时,应从文件里读取所有这些参数,而非从程序设置中读取。 其他设置仅影响视觉呈现,诸如以像素为单位的映像大小,显示细胞边界或显示字幕,不会保存在网络文件中,并且一旦网络教育之后,可重复和随机更改。
应该注意的是,未更新的类不会呈现带控件的图形用户界面 — 所有设置都是通过 MQL 程序的输入来指定。 与此同时,CSOMDisplay 类仍然实现了一些有用的功能。
回想一下,前面如何使用 Kohonen 网络的示例中,有一个名为 MaxPictures 的输入。 它在新的实现里依然存在。 它作为 maxpict 传递给方法 CSOMDisplay::Init,并设置图表中一行内显示的网络映像(平面)的数量。 将此参数与整体图像大小的 ImageW 和 ImageH 一起处理,我们可以找到一个选项,令所有映像都适合屏幕。 但是,当有许多映像时,譬如您必须分析 EA 的许多设置,其规模需要大幅降低,而这很不方便。 在这种情况下,您可以将参数 MaxPictures 设置为 0 来激活新模式。
在此模式下,在图表上所生成映像不是以像素坐标对齐的对象 OBJ_BITMAP_LABEL,而是与时间刻度对齐的对象 OBJ_BITMAP。 此类映像的大小可以增加,直到占满图表的整个高度,您可以使用常用的水平滚动条滚动它们,方法是用鼠标或滚轮或使用键盘拖拽它们。 映像数量不再限于屏幕尺寸。 然而,您应该确保柱线数量足够。
增加映像大小令我们更详尽地研究它们,尤其是类 CSOMDisplay 在细胞内可选择显示各种信息,例如相关平面的突触权重值,教育集矢量的命中数,平均值和命中细胞的所有矢量的相关特征值的离散度。 默认情况下不显示此信息,但如果您将鼠标光标停放在一个或另一个细胞上,则始终会弹出提示显示此信息。 弹出提示中还会显示当前平面的名称和神经元坐标。
此外,在任意神经元上双击将在当前映像和所有其他映像中同时高亮显示互补色的神经元。 这令我们可以同时直观比较所有特征的神经元活动。
最后,应当注意的是整个图形已经移到标准类 CCanvas 之中。 这会精简外部依赖的代码,但它也有副作用:Y 坐标现在按照自上而下的方式计数,而不像以前那样自下而上。 这导致在映像上方显示包含分量名称及其数值范围的图例,而非在其下方。 只是,这种变化似乎无关紧要。
在我们处理已有问题之前,需要对神经网络类进行一些改进。 除了表示特定特征的 2D 空间中的突触权重的标准映像之外,我们还将准备一些服务映像的计算和显示,这些服务映射是 Kohonen 网络的事实标准。 展望未来,我们会说在应用实验阶段,我们需要它们当中的中许多。
我们来定义附加维度的索引,总共会有 5 个。
#define EXTRA_DIMENSIONS 5 #define DIM_HITCOUNT (m_dimension + 0) #define DIM_UMATRIX (m_dimension + 1) #define DIM_NODEMSE (m_dimension + 2) // 每个节点的量化误差:平均方差(标准差的平方) #define DIM_CLUSTERS (m_dimension + 3) #define DIM_OUTPUT (m_dimension + 4)
U 型矩阵
首先,我们将计算 U 型矩阵,一个统一的距离矩阵,以便评估学习过程中在网络内产生的拓扑。 对于网络中的每个神经元,该矩阵包含该神经元与其直接相邻神经元之间的平均距离。 由于 Kohonen 网络将特征的多维空间显示在映像的二维空间中。 折叠发生在这个二维空间中。 换言之,尽管 Kohonen 网络的特性是保持初始空间固有的排列,但它在整个 2D 空间中同样无法实现,并且神经元的地理接近度变得虚幻。 恰好 U 型矩阵用于检测这些区域。 其中,神经元权重与其相邻神经元权重之间存在较大差值的区域显示为“峰值”,而神经元非常相似的区域则显示为“洼地”。
若要计算神经元和特征矢量之间的距离,则有 CSOMNode::CalculateDistance 方法。 我们将为它创建一个对应的方法,它将指针指向另一个神经元而来替代向量(数组 'double')。
double CSOMNode::CalculateDistance(const CSOMNode *other) const { double vector[]; other.GetCodeVector(vector); return CalculateDistance(vector); }
此处,方法 GetCodeVector 获取另一个神经元的权重数组,并立即将其按照常规方式计算距离。
为了获得统一的神经元距离,有必要计算到其所有相邻神经元的距离并求它们的平均值。 由于相邻神经元的遍历是网络网格的若干操作的常见任务,我们将为遍历创建一个基类,然后在其后代中实现单独算法,包括汇总距离。
#define NBH_SQUARE_SIZE 4 #define NBH_HEXAGONAL_SIZE 6 template<typename T> class Neighbourhood { protected: int neighbours[]; int nbhsize; bool hex; int m_ycells; public: Neighbourhood(const bool _hex, const int ysize) { hex = _hex; m_ycells = ysize; if(hex) { nbhsize = NBH_HEXAGONAL_SIZE; ArrayResize(neighbours, NBH_HEXAGONAL_SIZE); neighbours[0] = -1; // 上 (可视) neighbours[1] = +1; // 下 (可视) neighbours[2] = -m_ycells; // 左 neighbours[3] = +m_ycells; // 右 /* 模板,在下面的循环中动态应用 // 奇数行 neighbours[4] = -m_ycells - 1; // 左上 neighbours[5] = -m_ycells + 1; // 左下 // 偶数行 neighbours[4] = +m_ycells - 1; // 右上 neighbours[5] = +m_ycells + 1; // 右下 */ } else { nbhsize = NBH_SQUARE_SIZE; ArrayResize(neighbours, NBH_SQUARE_SIZE); neighbours[0] = -1; // 上 (可视) neighbours[1] = +1; // 下 (可视) neighbours[2] = -m_ycells; // 左 neighbours[3] = +m_ycells; // 右 } } ~Neighbourhood() { ArrayResize(neighbours, 0); } T loop(const int ind, const CSOMNode &p_node[]) { int nodes = ArraySize(p_node); int j = ind % m_ycells; if(hex) { int oddy = ((j % 2) == 1) ? -1 : +1; neighbours[4] = oddy * m_ycells - 1; neighbours[5] = oddy * m_ycells + 1; } reset(); for(int k = 0; k < nbhsize; k++) { if(ind + neighbours[k] >= 0 && ind + neighbours[k] < nodes) { // 跳过包边 if(j == 0) // 顶行 { if(k == 0 || k == 4) continue; } else if(j == m_ycells - 1) // 底行 { if(k == 1 || k == 5) continue; } iterate(p_node[ind], p_node[ind + neighbours[k]]); } } return getResult(); } virtual void reset() = 0; virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) = 0; virtual T getResult() const = 0; };
根据传递给构造函数的网格类型,邻域数量 nbhsize 等于 4 和 6。 与当前神经元相关的相邻神经元数量的增量存储在“neighbours”数组当中。 例如,在正方形网格中,从高层神经元减一层,或从底层神经元加一层来得到上一层相邻神经元。 左右相邻神经元的数字与网格的列高度不同,因此该值作为 ysize 传递给构造函数。
相邻神经元的真实遍历由方法 'loop' 执行。 类 Neighborhood 当中不包含任何神经元数组,因此它作为参数传递给方法 'loop'。
在循环中此方法跨越数组“neighbours”,并另行检查相邻神经元的数量是否超出网格,要考虑增量。 对于全部的有效数字,调用抽象方法 'iterate',其中要传递当前神经元和围绕神经元之一的链接。
在循环之前调用抽象方法 'reset',在循环之后调用抽象方法 getResult。 一组三个抽象方法允许在后代类中准备和执行相邻神经元的枚举并生成结果。 “loop”方法构造概念对应于已知的 OOP 设计范式 — 模板方法。 在此,我们应该将范式本名中的“模板”术语与模板的语言范式区分开来,模板的语言范式也在类 Neighbourhood 中使用,因为它是模板,即 ,它由某个变量类型 T 进行参数化。特别是,'loop' 方法本身和方法 getResult 返回T类型的值。
基于类 Neighbourhood,我们将编写一个类来计算 U 型矩阵。
class UMatrixNeighbourhood: public Neighbourhood<double> { private: int n; double d; public: UMatrixNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize) { } virtual void reset() override { n = 0; d = 0.0; } virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override { d += node1.CalculateDistance(&node2); n++; } virtual double getResult() const override { return d / n; } };
处理类型是双精度。 通过其基类,距离的计算是相当透明的。
我们将在方法 CSOM::CalculateDistances 中计算整个映像的距离。
void CSOM::CalculateDistances() { UMatrixNeighbourhood umnh(m_hexCells, m_ycells); for(int i = 0; i < m_xcells * m_ycells; i++) { double d = umnh.loop(i, m_node); if(d > m_max[DIM_UMATRIX]) { m_max[DIM_UMATRIX] = d; } m_node[i].SetDistance(d); } }
统一距离的值保存在神经元的对象中。 稍后,当显示所有平面时,我们将能够使用调色板以标准方式定义距离值,并在计算中包括附加尺寸 DIM_UMATRIX。 为了正确地缩放调色板,我们在该方法中保存了相关数组 m_max 元素范围内的最高距离值(所有实现原理与先前的实现保持不变)。
命中次数和量化误差
下一个附加维度将收集特定神经元中学习矢量命中数的统计数据。 换言之,它是所用数据填充神经元的密度。 在特定神经元中越高,其权重因子在统计上越合理。 在网络中,神经元也许发生较小甚或为零的数据覆盖。 也许会有很多,这也许说是选择网络大小或在多维空间的 2D 投影中拓扑扭曲的问题。 通过以下方法计算样品到某个神经元的命中率:
void CSOMNode::RegisterPatternHit(const double &vector[]) { m_hitCount++; double e = 0; for(int i = 0; i < m_dimension; i++) { m_sum[i] += vector[i]; m_sumP2[i] += vector[i] * vector[i]; e += (m_weights[i] - vector[i]) * (m_weights[i] - vector[i]); } m_mse += e / m_dimension; }
计数本身在第一个 m_hitCount++ 字符串中执行,其中内部计数器增加。 其余执行其他有用的工作的代码,将在下面讨论。
我们将自 CSOM 类完成学习之后调用方法 RegisterPatternHit,在那里我们将创建一个特殊的统计方法来处理每个矢量。
double CSOM::AddPatternStats(const double &data[]) { static double vector[]; ArrayCopy(vector, data); int ind = GetBestMatchingIndex(vector); m_node[ind].RegisterPatternHit(vector); double code[]; m_node[ind].GetCodeVector(code); Denormalize(code); double mse = 0; for(int i = 0; i < m_dimension; i++) { mse += (data[i] - code[i]) * (data[i] - code[i]); } mse /= m_dimension; return mse; }
作为一个题外话,应该注意这里使用的方法 GetBestMatchingIndex,以及 GetBestMatchingXYZ 方法组中的其他一些方法,常规化了自身内部的传入数据,因此有必要传递一个矢量的副本。 否则,在调用代码中可能稀里糊涂地修改了源数据。
除了重新编码 hit 之外,该方法还计算当前神经元和所传递矢量的量化误差。 为此目的,从获胜的神经元中调用所谓的代码 vector,即 ,突触权重数组,并计算权重和输入矢量之间的分量差值的平方和。
对于 AddPatternStatsm,它立即从另一个方法 CSOM::CalculateStats 调用,它只为所有输入分配循环。
double CSOM::CalculateStats(const bool complete = true) { double data[]; ArrayResize(data, m_dimension); double trainedMSE = 0.0; for(int i = complete ? 0 : m_validationOffset; i < m_nSet; i++) { ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension); trainedMSE += AddPatternStats(data, complete); } double nmse = trainedMSE / m_dataMSE; if(complete) Print("Overall NMSE=", nmse); return nmse; }
该方法对所有量化误差进行求和,并将它们与输入数据的离散度 m_dataMSE 进行比较 — 这正是上述验证和学习停止章节里描述的 NMSE 计算。 该方法提到了在创建 CSOM 对象时指定的变量 m_validationOffset,此对象基于是否将输入数据集划分为学习和验证子集。
您猜对了,方法 CalculateStats 在 Train 方法内的每个时期被调用(如果收敛阶段已经开始),我们可以通过返回值判断整个网络误差是否已经开始增加,即 ,是否到了停止时刻。
预先计算离散度 m_dataMSE,使用以下方法:
void CSOM::CalculateDataMSE() { double data[]; m_dataMSE = 0.0; for(int i = m_validationOffset; i < m_nSet; i++) { ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension); double mse = 0; for(int k = 0; k < m_dimension; k++) { mse += (data[k] - m_mean[k]) * (data[k] - m_mean[k]); } mse /= m_dimension; m_dataMSE += mse; } }
我们已经在数据常规化阶段中获得了每个分量的平均值 m_mean。
void CSOM::InitNormalization(const bool normalization = true) { ArrayResize(m_max, m_dimension + EXTRA_DIMENSIONS); ArrayResize(m_min, m_dimension + EXTRA_DIMENSIONS); ArrayInitialize(m_max, 0); ArrayInitialize(m_min, 0); ArrayResize(m_mean, m_dimension); ArrayResize(m_sigma, m_dimension); for(int j = 0; j < m_dimension; j++) { double maxv = -DBL_MAX; double minv = +DBL_MAX; if(normalization) { m_mean[j] = 0; m_sigma[j] = 0; } for(int i = 0; i < m_nSet; i++) { double v = m_set[m_dimension * i + j]; if(v > maxv) maxv = v; if(v < minv) minv = v; if(normalization) { m_mean[j] += v; m_sigma[j] += v * v; } } m_max[j] = maxv; m_min[j] = minv; if(normalization && m_nSet > 0) { m_mean[j] /= m_nSet; m_sigma[j] = MathSqrt(m_sigma[j] / m_nSet - m_mean[j] * m_mean[j]); } else { m_mean[j] = 0; m_sigma[j] = 1; } } }
转向附加平面,应该注意的是,在 CSOMNode::RegisterPatternHit 中计算后,每个神经元都能够使用以下方法返回相关的统计数据:
int CSOMNode::GetHitsCount() const { return m_hitCount; } double CSOMNode::GetHitsMean(const int plane) const { if(m_hitCount == 0) return 0; return m_sum[plane] / m_hitCount; } double CSOMNode::GetHitsDeviation(const int plane) const { if(m_hitCount == 0) return 0; double z = m_sumP2[plane] / m_hitCount - m_sum[plane] / m_hitCount * m_sum[plane] / m_hitCount; if(z < 0) return 0; return MathSqrt(z); } double CSOMNode::GetMSE() const { if(m_hitCount == 0) return 0; return m_mse / m_hitCount; }
因此,我们得到填充两个平面的数据 — 通过神经元和量化误差显示输入矢量的数量。
网络响应
下一个附加平面将是对特定样本的礼让(yield)映像和网络响应。 应该回想一下,在向网络投喂信号时,除了获胜的神经元,所有其他神经元的激活程度都较小。 比较主动响应偏移的可能性有助于定义由网络提议的解决方案的稳定性。
网络响应计算最简单。 在 CSOMNode 类中,我们将编写以下方法:
double CSOMNode::CalculateOutput(const double &vector[]) { m_output = CalculateDistance(vector); return m_output; }
我们将为网络类中的每个神经元调用它。
void CSOM::CalculateOutput(const double &vector[], const bool normalize = false) { double temp[]; ArrayCopy(temp, vector); if(normalize) Normalize(temp); m_min[DIM_OUTPUT] = DBL_MAX; m_max[DIM_OUTPUT] = -DBL_MAX; for(int i = 0; i < ArraySize(m_node); i++) { double x = m_node[i].CalculateOutput(temp); if(x < m_min[DIM_OUTPUT]) m_min[DIM_OUTPUT] = x; if(x > m_max[DIM_OUTPUT]) m_max[DIM_OUTPUT] = x; } }
如果不能向程序提供测试矢量,则默认计算响应,即零矢量。
聚类
最后,研究最后一个平面,大概也是最重要的平面,就是集群映像。 在二维映像上安排输入数据只是战斗的一半。 分析的真正目的是检测功能并将其分类为易于理解的应用条款类别。 在特征空间的维度相对较小的情况下,我们可以通过各个平面上的彩色斑点来轻易地区分具有所需特征的区域,这些斑点通常是被隔离的。 不过,随着输入数据结构的扩展,图像变得更加复杂,并且替代交叉分析数十个具有不同索引的映像,更便利的方法是将一个映像划分为醒目的区域。
聚类将导致两种结果,即通过具有相似特征的区域标记映像,并识别集群的中心。 然后我们可以认为它们是最具代表性的,在统计学上,是相关类的样本。 至此,我们逐渐接近选择最佳 EA 参数的任务。 但是,我们应该实现聚类。
K 均值
有很多聚类方法。 对于 MQL5,最简单的选择是使用 ALGLIB 的版本,它包含在标准库中。 包含头文件就足够了:
#include <Math/Alglib/dataanalysis.mqh>
并编写一个这样的方法:
void CSOM::Clusterize(const int clusterNumber) { int count = m_xcells * m_ycells; CMatrixDouble xy(count, m_dimension); int info; CMatrixDouble clusters; int membership[]; double weights[]; for(int i = 0; i < count; i++) { m_node[i].GetCodeVector(weights); xy[i] = weights; } CKMeans::KMeansGenerate(xy, count, m_dimension, clusterNumber, KMEANS_RETRY_NUMBER, info, clusters, membership); Print("KMeans result: ", info); if(info == 1) // ok { for(int i = 0; i < m_xcells * m_ycells; i++) { m_node[i].SetCluster(membership[i]); } ArrayResize(m_clusters, clusterNumber * m_dimension); for(int j = 0; j < clusterNumber; j++) { for(int i = 0; i < m_dimension; i++) { m_clusters[j * m_dimension + i] = clusters[i][j]; } } } }
它使用 K-均值 执行聚类算法。 不幸的是,据我所知,它是 MQL5 的 ALGLIB 版本中唯一的聚类算法,尽管原始函数库的最新版本提供了其他算法,例如 凝聚层次聚类。
之所以 “不幸的是”,因为算法 K-均值在某种程度上是最“直线”的:它的本质是减少在特征空间内搜索给定数量球体的中心,它以最有效的方式覆盖采样点,即 ,自集群中心到采样点的距离的平方和的最小值。 问题在于,由于它们的固定形式,球状体在非线性聚类的可分离性方面具有一些特定的限制。 原则上,K-均值是算法 期望最大化 的特殊情况,它操作不同取向和形式的椭球,因此更优选。 然而,即使在使用它时,也存在粘附在局部最小值的可能性,因为两种算法都使用凸形和聚类中心的随机排列。 缺点还包括必须事先指定聚类数量的事实。
但是,我们研究如何使用 ALGLIB 中的 K-均值来安排聚类。 主要操作由 CKMeans::KMeansGenerate 方法执行。 我们为其传递一个数组,其中源数据采用特殊的基于对象的格式(CMatrixDouble xy),矢量数量(count),特征空间的维数(m_dimension)和所需的聚类(clusterNumber),后者在 MQL 程序的参数中指定。 下一个输入 KMEANS_RETRY_NUMBER 是迭代次数,该值取决于算法而不同,随机选择的初始中心,试图避免局部解决方案。 在我们的例子中,它是一个等于 10 的宏定义。 作为函数操作的结果,我们将获得名为 'info' 的执行代码(不同的值表示成功或错误),基于聚类对象的数组名为 CMatrixDouble,含有聚类坐标,输入数组是聚类成员(membership)。
我们将聚类中心保存在数组 m_clusters 中,以便在映像上标记它们,并且根据其聚类成员资格相关的颜色为每个神经元着色:
m_node[i].SetCluster(membership[i]);
当利用 ALGLIB 操作时,请记住它使用自己的随机数生成器来考虑特殊静态对象的内部状态。 所以,即使通过 MathSrand 对标准生成器进行显式初始化也不会重置其状态。 这对于 EA 尤其重要,因为在更改设置时不会在其中重新生成全局对象。 因此,如果在 OnInit 中 CMath::m_state 未清零,则可能会导致 ALGLIB 难以重现计算结果。
考虑到 K-均值的上述缺点,期望能有替代的聚类方法。 另一种替代方案显而易见。
替代方案
我们把注意力转向 Kohonen 映像,特别是我们引入的其他维度。 U 型矩阵特别令人感兴趣。 该平面展现出了最接近的神经元的区域,即,它们在 2D 映像拓扑方面和在特征空间方面都接近。 如同我们的记忆,U 型矩阵中有一种类似“洼地”的神经元。 它们是变成聚类的很好候选者。
我们可以将统一距离的映像转换成聚类,例如,以下面的方式。
将所有神经元的信息复制到一个数组中,然后按 U 型距离的值(CSOMNode::GetDistance())对其进行排序。
对于给定的神经元,我们将在循环中检查数组,相邻神经元是否属于一个聚类。
这很简单。 不应该考虑神经元的填充密度吗? 毕竟,U 型距离对于具有不同命中数的神经元具有不同的支持。 换言之,如果两个神经元具有相同的 U 型距离,则其中一个已显示更多样本的神经元,比之较低样本数量的神经元更具优势。
然后,按照公式 CSOMNode::GetDistance() / sqrt(CSOMNode::GetHitsCount())中的数值顺序修改所述算法中的初始数组排序就足够了。 我增加了平方根,以便在密度较大的情况下平滑其影响,而密度较小时应该“惩治(punished)”更严格。
不过,如果我们使用两个服务平面,那么分析第三个服务平面可能是合理的,即 ,那个量化误差? 实际上,在特定神经元中量化误差越大,我们应该越少信任其中的较小 U 型距离信息,反之亦然。
如果我们记得出现过的量化误差函数:
double CSOMNode::GetMSE() const { if(m_hitCount == 0) return 0; return m_mse / m_hitCount; }
然后我们将很容易地注意到在其中使用了命中计数器 m_hitCount (仅在分母中)。 所以,我们可以重新编写前面的公式,将神经元数组按照 CSOMNode::GetDistance() * MathSqrt(CSOMNode::GetMSE())排序 — 然后将考虑所有三个附加索引,我们已将它们添加到我们的 Kohonen 网络实现。
我们几乎准备好了呈现聚类算法的最终替代形式,但仍然存在一个小问题。 在神经元数组的循环内部,我们应该检查当前神经元的邻域是否存在相邻的聚类。 稍早一点,我们实现了模板类 Neighborhood,用于局部瞭望。 现在,我们将创建其后代,专注于搜索聚类。
class ClusterNeighbourhood: public Neighbourhood<int> { private: int cluster; public: ClusterNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize) { } virtual void reset() override { cluster = -1; } virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override { int x = node2.GetCluster(); if(x > -1) { if(cluster != -1) cluster = MathMin(cluster, x); else cluster = x; } } virtual int getResult() const override { return cluster; } };
该类包含潜在聚类的数量(该数字是整数,因此我们使用 int 类型对模板进行参数化)。 最初,此变量在 reset 方法中初始化为 -1,即 ,没有聚类。 然后,随着父类从其循环方法调用我们的新实现 'iterate',我们得到每个相邻神经元的聚类数量,将其与聚类进行比较,并保存最小值。 如果没有找到聚类,则由 getResult 方法返回相同或 -1。
作为改进,我们建议跟踪神经元之间的“峰值高度”,即 ,node1.CalculateDistance(&node2) 的值,并且只有当“高度”低于前值时,聚类数量才能执行从一个神经元“流动”到另一个神经元。 最终的实现版本已在源代码中提供。
最后,我们可以实现替代聚类。
void CSOM::Clusterize() { double array[][2]; int n = m_xcells * m_ycells; ArrayResize(array, n); for(int i = 0; i < n; i++) { if(m_node[i].GetHitsCount() > 0) { array[i][0] = m_node[i].GetDistance() * MathSqrt(m_node[i].GetMSE()); } else { array[i][0] = DBL_MAX; } array[i][1] = i; m_node[i].SetCluster(-1); } ArraySort(array); ClusterNeighbourhood clnh(m_hexCells, m_ycells); int count = 0; // 聚类数量 ArrayResize(m_clusters, 0); for(int i = 0; i < n; i++) { // 如果已经分配则跳过 if(m_node[(int)array[i][1]].GetCluster() > -1) continue; // 检查当前节点是否与任何现有聚类相邻 int r = clnh.loop((int)array[i][1], m_node); if(r > -1) // 邻居已经属于聚类 { m_node[(int)array[i][1]].SetCluster(r); } else // 我们需要新的聚类 { ArrayResize(m_clusters, (count + 1) * m_dimension); double vector[]; m_node[(int)array[i][1]].GetCodeVector(vector); ArrayCopy(m_clusters, vector, count * m_dimension, 0, m_dimension); m_node[(int)array[i][1]].SetCluster(count++); } } }
该算法实际上完全遵循上述的口语化伪代码:我们填充二维数组(来自第一维中的公式值,和第二维中的神经元索引),排序,在循环中访问所有神经元,并分析它们每一个的邻居。
当然,聚类的质量应该在实践中进行评估,我预先假定存在拓扑问题。 然而,考虑到大多数经典的聚类方法也存在问题,并且这个提议比较拙劣,而新的解决方案看起来很有吸引力。
而这种实现的优点中,我要提到这样一个事实:聚类按其重要性排列(在上述 K-均值中,聚类相等),它们的形式是随机的,并且数量不需要预先定义。 应当注意的是,最后一条具有反面,即 ,聚类的数量可能相当大。 除此之外,按照内容相似度和最小误差安排的聚类,实际上可以仅考虑前 5-10 个聚类,并将其他聚类留在“幕后”。
由于我没有在任何开源中找到任何类似的聚类方法,我建议将它命名为 Korotky 聚类,或者更长但得体 — 基于 U 型矩阵和量化误差(QE)的短路径聚类。
我应该言之在前,在许多测试中,实践证明,K-均值算法发现的聚类中心的聚类结果比选择性聚类(至少在优化结果分析问题上)的聚类结果差。 因此,在下文中仅意指和应用该聚类方法。
现在是时候从理论转向实践,并测试网络如何运作。 我们创建一个简单,通用的智能交易系统,其中包含演示基本功能的选项。 我们将其命名为 SOM-Explorer。
我们包含上述的类头文件。 定义输入。
分组 — 网络结构和数据设置
分组 - 可视化
分组 - 选项
这些只是基本设置。 在我们继续解决问题时,我们将添加一些其他特殊参数。
请注意! EA 会更改当前图表的设置— 打开一个新图表专门用来操作此 EA。
CSOMDisplay 类对象将在 EA 中执行所有操作。
CSOMDisplay KohonenMap;
在初始化期间,不要忘记启用鼠标移动事件处理 — 该类使用它们来显示弹出提示以及滚动。
void OnInit() { ChartSetInteger(0, CHART_EVENT_MOUSE_MOVE, true); EventSetMillisecondTimer(1); } void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam) { KohonenMap.OnChartEvent(id, lparam, dparam, sparam); }
神经网络算法(学习或测试)仅应在 EA 中启动一次 — 通过计时器,然后禁用计时器。
void OnTimer() { EventKillTimer(); MathSrand(RandomSeed); bool hasOneTestPattern = false; if(NetFileName != "") { if(!KohonenMap.Load(NetFileName)) return; KohonenMap.DisplayInit(ImageW, ImageH, MaxPictures, ColorScheme, ShowBorders, ShowTitles); Comment("Map ", NetFileName, " is loaded; size: ", KohonenMap.GetWidth(), "*", KohonenMap.GetHeight(), "; features: ", KohonenMap.GetFeatureCount());
如果已指定了含网络的文件,我们加载它并根据可视设置准备显示。
if(DataFileName != "") { if(!KohonenMap.LoadPatterns(DataFileName)) { Print("Data loading error, file: ", DataFileName); // 生成随机测试矢量 int n = KohonenMap.GetFeatureCount(); double min, max; double v[]; ArrayResize(v, n); for(int i = 0; i < n; i++) { KohonenMap.GetFeatureBounds(i, min, max); v[i] = (max - min) * rand() / 32767 + min; } KohonenMap.AddPattern(v, "RANDOM"); Print("Random Input:"); ArrayPrint(v); double y[]; CSOMNode *node = KohonenMap.GetBestMatchingFeatures(v, y); Print("Matched Node Output (", node.GetX(), ",", node.GetY(), "); Hits:", node.GetHitsCount(), "; Error:", node.GetMSE(),"; Cluster N", node.GetCluster(), ":"); ArrayPrint(y); KohonenMap.CalculateOutput(v, true); hasOneTestPattern = true; } }
如果指定了包含测试详细信息的文件,我们会尝试加载它。 如果它不起作用,则在日志中显示一条消息,并生成随机测试数据样本。利用 GetFeatureCount 和 GetFeatureBounds 方法定义特征数量(矢量的维数)及其允许的范围。 然后,通过调用 AddPattern,将样本添加到名为 RANDOM 的工作数据集中。
该方法适用于自未支持格式的数据源形成教育选择,例如数据库,并用来直接从指标填充它们。 原则上,在这种特定情况下,只需要将样本添加到工作集中,以便随后在映像上显示它们(如下所示),而只调用一次 GetBestMatchingFeatures 足以在网络中找到最合适的神经元。 该方法来自若干可用的 GetBestMatchingXYZ 方法,它能令我们得到数组 y 中获胜神经元特征的相关值。 最后,使用 CalculateOutput,我们在附加平面中显示对测试样本的网络响应。
我们继续关注 EA 代码。
} else // 未提供网络文件,因此假定进行训练 { if(DataFileName == "") { // 生成无缩放值的 3D 演示矢量 {[0,+1000], [0,+1], [-1,+1]} // 将它们投喂到网络中以便比较有无常规化的结果 // 注意 标题应该是有效的 BMP 文件名 string titles[] = {"R1000", "R1", "R2"}; KohonenMap.AssignFeatureTitles(titles); double x[3]; for(int i = 0; i < 1000; i++) { x[0] = 1000.0 * rand() / 32767; x[1] = 1.0 * rand() / 32767; x[2] = -2.0 * rand() / 32767 + 1.0; KohonenMap.AddPattern(x, StringFormat("%f %f %f", x[0], x[1], x[2])); } }
如果未指定已教育网络,我们假设学习模式。 检查是否有任何输入。 如果没有,我们生成一组随机的三维矢量,其中第一个分量在 [0,+1000] 范围内,第二个分量在 [0,+1] 范围内,第三个分量在 [1,+1] 范围内。 分量的名称使用 AssignFeatureTitles 传递到网络,而数据 — 使用已知的 AddPattern。
else // 提供了一个数据文件 { if(!KohonenMap.LoadPatterns(DataFileName)) { Print("Data loading error, file: ", DataFileName); return; } }
如果输入来自文件,则加载此文件。 如果出现错误,结束操作,因为没有网络或数据。
进而,我们执行教育和聚类。
KohonenMap.Init(CellsX, CellsY, ImageW, ImageH, MaxPictures, ColorScheme, HexagonalCell, ShowBorders, ShowTitles); if(ValidationSetPercent > 0 && ValidationSetPercent < 50) { KohonenMap.SetValidationSection((int)(KohonenMap.GetDataCount() * (1.0 - ValidationSetPercent / 100.0))); } KohonenMap.Train(EpochNumber, UseNormalization, ShowProgress); if(ClusterNumber > 1) { KohonenMap.Clusterize(ClusterNumber); } else { KohonenMap.Clusterize(); } }
如果未指定单个测试样本的分析(特别是,在学习之后马上),我们默认情况下形成针对零矢量的网络响应。
if(!hasOneTestPattern) { double vector[]; ArrayResize(vector, KohonenMap.GetFeatureCount()); ArrayInitialize(vector, 0); KohonenMap.CalculateOutput(vector); }
然后我们在图形资源的内部缓冲区中绘制所有映像 — 首先是背后的颜色:
KohonenMap.Render(); // 将映像绘制到内部 BMP 缓冲区中
然后,标题:
if(hasOneTestPattern) KohonenMap.ShowAllPatterns(); else KohonenMap.ShowAllNodes(); // 在 BMP 缓冲区中绘制细胞内标签
标记聚类:
if(ClusterNumber != 0) { KohonenMap.ShowClusters(); // 标记聚类 }
在图表上显示缓冲区,并可选择将图像保存到文件中:
KohonenMap.ShowBMP(SaveImages); // 在图表上将文件显示为位图图像,可选择保存到文件中
这些文件放在一个单独的文件夹中,该文件夹的名称与网络文件的名称相同(如果已提供),或者包含数据的文件(如果已提供)。 如果数据文件尚未指定,且网络已依据随机生成的数据完成学习,则使用 SOM 前缀以及当前日期和时间形成 som 文件的名称和包含图像的文件夹。
最后,将已完成学习的网络保存到文件中。 如果已在 NetFileName 中指定了网络名称,则表示 EA 已在测试模式下工作,因此我们无需再次保存网络。
if(NetFileName == "") { KohonenMap.Save(KohonenMap.GetID()); } }
我们将尝试通过生成测试随机数据来启动 EA。 使用所有默认设置,除了用于确保所有平面都能进入屏幕截图的图像下调,ImageW = 230,ImageH = 230,MaxPictures = 3,我们获得以下图片:
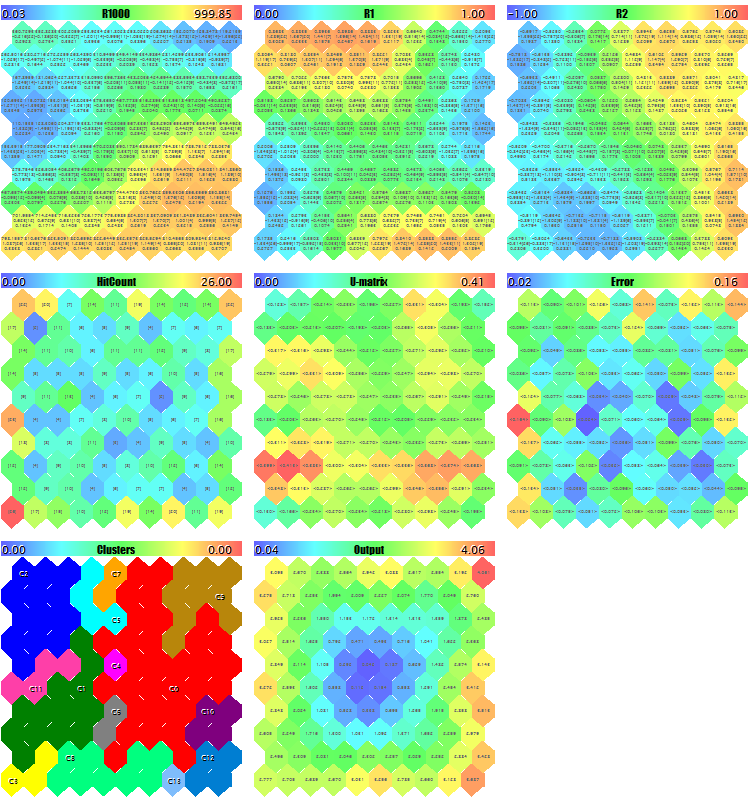
样本 Kohonen 映像随机 3D 矢量
此处,服务数据显示在每个神经元中(您可以通过鼠标光标指点来查看详细信息),并标记已发现的聚类。
在该过程中,日志中显示以下信息(聚类信息限定为 5; 您可以在源代码中更改它):
Pass 0 from 1000 0% Pass 78 from 1000 7% Pass 157 from 1000 15% Pass 232 from 1000 23% Pass 310 from 1000 31% Pass 389 from 1000 38% Pass 468 from 1000 46% Pass 550 from 1000 55% Pass 631 from 1000 63% Pass 710 from 1000 71% Pass 790 from 1000 79% Pass 870 from 1000 87% Pass 951 from 1000 95% Overall NMSE=0.09420336270396877 Training completed at pass 1000, NMSE=0.09420336270396877 Clusters [14]: "R1000" "R1" "R2" N0 754.83131 0.36778 0.25369 N1 341.39665 0.41402 -0.26702 N2 360.72925 0.86826 -0.69173 N3 798.15569 0.17846 -0.37911 N4 470.30648 0.52326 0.06442 Map file SOM-20181205-134437.som saved
如果现在我们为参数 NetFileName 中的网络指定所创建的 SOM-20181205-134437.som 文件名称,并在参数 DataFileName 中输入 '?',我们将获得的测试运行结果不是来自学习集,而是随机样本。 为了更好地查看映像,我们将它们的尺寸放大,并将 MaxPictures 设置为 0。

Kohonen 映像随机 3D 矢量的前两个分量
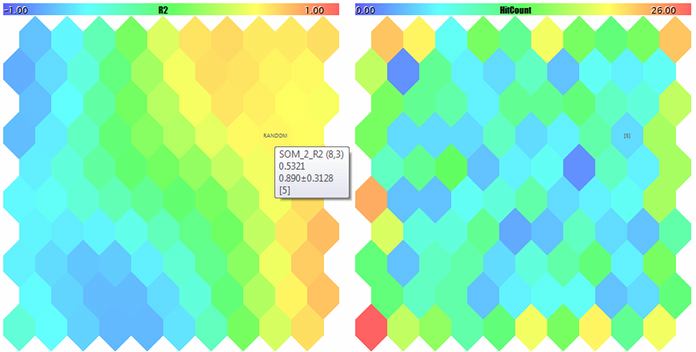
Kohonen 映像,用于随机 3D 矢量的第三个分量和命中计数器
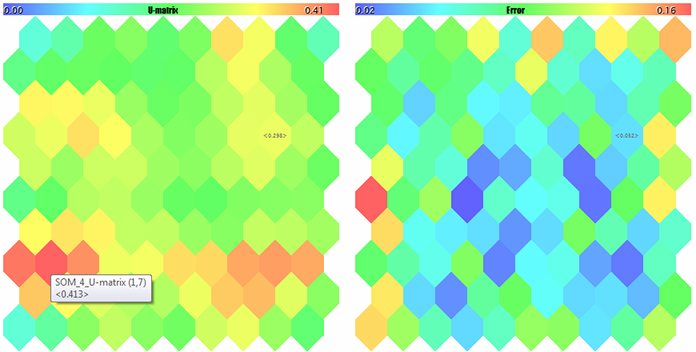
U 型矩阵和量化误差
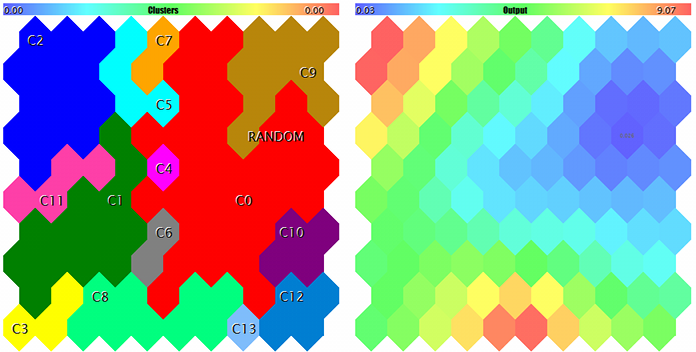
聚类和 Kohonen 网络对测试样本的响应
样品标有 RANDOM。 当鼠标光标指向点时,会弹出有关神经元的提示。 日志中会显示类似以下内容:
FileOpen error ?.csv : 5004 Data loading error, file: ? Random Input: 457.17510 0.29727 0.57621 Matched Node Output (8,3); Hits:5; Error:0.05246704285146882; Cluster N0: 497.20453 0.28675 0.53213
因此,操作 Kohonen 网络的工具已准备就绪。 我们可以去解决问题。 我们将在第二篇文章中对此进行处理。
近几年来,Kohonen 神经网络的开放式实现已经提供给 MetaTrader 用户。 我们已修复了它们当中的一些错误,辅以有用的工具,并使用特殊的演示 EA 测试了它们的操作。 源代码可令您将这些类应用到自己的任务里; 我们将进一步研究相关的例子 — 未完待续。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
