请　[注册]　或　[登录]　 | 返回主站

量化交易吧 /  量化平台 帖子：3364744 新帖：8

可视化！类似于 R 语言 "plot (绘图)" 的 MQL5 图形库

外汇老法师发表于：4 月 17 日 18：37回复(1)

在研究交易逻辑时, 图形形式的直观表达是非常重要的。科学界中流行的一些编程语言 (如 R 和 Python) 拥有可视化的特殊 "plot (绘图)" 功能。它能够以直观方式绘制线, 点分布和直方图。

"plot" 函数的重要优点就是您只需要几行代码即可绘制任何图形。简单地传递数据数组作为参数, 指定图形类型, 您即准备好上路了！"绘图" 函数进行比例计算, 构建坐标轴, 选择颜色等所有常规操作。

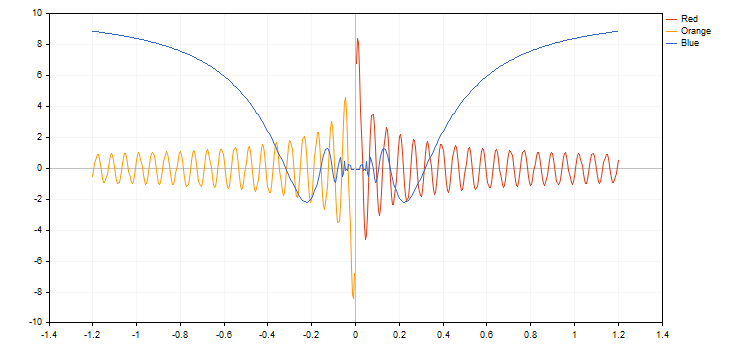
在 MQL5 中, 函数的所有功能都由标准库中的 图形库 方法来表达。示例代码及其执行结果如下所示:

#include <Graphics\Graphic.mqh>
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- 函数
double BlueFunction(double x)   { return(RESULT_OR_NAN(x,10*x*sin(1/x)));      }
double RedFunction(double x)    { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//| 脚本的 start 函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from=-1.2;
   double to=1.2;
   double step=0.005;
   CGraphic graphic;
   graphic.Create(0,"G",0,30,30,780,380);
//--- 颜色
   CColorGenerator generator;
   uint blue= generator.Next();
   uint red = generator.Next();
   uint orange=generator.Next();
//--- 绘制所有曲线
   graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"红色");
   graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"橙色");
   graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"蓝色");
   graphic.CurvePlotAll();
   graphic.Update();
  }



CCanvas 基类及其开发

标准库包含的 CCanvas 基类, 设计用于直接在价格图表上快速方便地绘制图像。该类在创建图形 资源 基础上, 在画板上绘制简单的基元 (点, 直线和折线, 圆, 三角形和多边形)。该类实现了形状填充, 使用必要的字体、颜色和字号显示文本的功能。

最初, CCanvas 仅包含两个显示图形基元的模式 — 抗锯齿 (AA) 和无抗锯齿。之后, 添加了基于 吴小林算法 绘制图元的新函数:

  • LineWu — 直线
  • PolylineWu — 折线
  • PolygonWu — 多边形
  • TriangleWu — 三角形
  • CircleWu — 圆形
  • EllipseWu — 椭圆

吴小林的算法结合了高品质的混叠消隐, 且速度接近无抗锯齿的 Bresenham 算法。它与 CCanvas 实现的标准抗锯齿算法 (AA) 在视觉上有所不同。以下是使用三种不同函数绘制圆形的示例:

#include<Canvas\Canvas.mqh>
CCanvas canvas;
//+------------------------------------------------------------------+
//| 脚本的 start 函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
   int      Width=800;
   int      Height=600;
//--- 创建画板
   if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
     {
      Print("创建画板错误: ",GetLastError());
     }
//--- 绘图
   canvas.Erase(clrWhite);
   canvas.Circle(70,70,25,clrBlack);
   canvas.CircleAA(120,70,25,clrBlack);
   canvas.CircleWu(170,70,25,clrBlack);
//---
   canvas.Update();  
  }


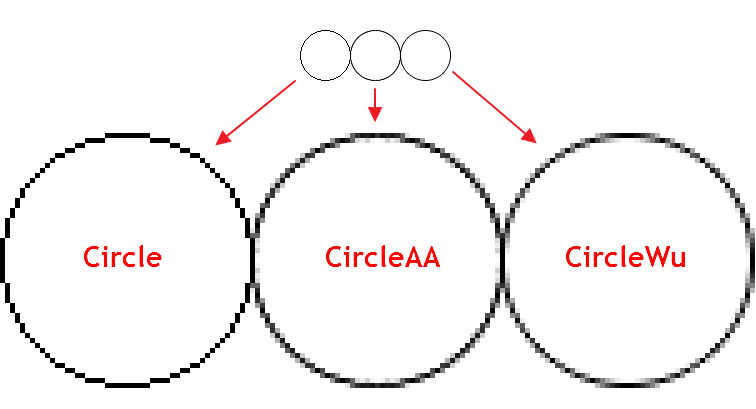
正如我们所见, CircleAA() 标准平滑算法相较于根据吴小林算法 CircleWu() 函数绘制的线条较粗。由于其较细且过渡色调计算更好, CircleWu 看起来更加整洁自然。

在 CCanvas 类中还有其它改进:

  1. 添加了新的带有两个抗锯齿选项的 椭圆 图元 — EllipseAA() 和 EllipseWu()
  2. 添加了重载的 区域填充函数, 新参数负责 "填充敏感度" (阀值参数)。


函数库的操作算法

1. 连接函数库之后, 我们应创建 CGraphic 类的对象。要绘制的曲线将会添加到它之内。

接下来, 我们应为创建的对象调用Create() 方法。方法包含主要图形参数:

  1. 图形 ID
  2. 对象名
  3. 窗口索引
  4. 图形锚点
  5. 图形宽度和高度

该方法利用定义的参数来创建图表对象, 以及绘制图形时要用到的图形资源。

   //--- 创建图形对象
   CGraphic graphic;
   //--- 创建画板
   graphic.Create(0,"Graphic",0,30,30,830,430);

结果就是, 我们有了一个现成的画板。

2. 现在, 我们用曲线来填充对象。使用 CurveAdd() 方法以四种不同方式绘制曲线:

  1. 基于双精度类型的一维数组。在此情况下, 来自数组的数值显示在 Y 轴, 二数组的索引作为 X 坐标。
  2. 基于两个双精度数组 x[] 和 y[]。
  3. 基于 CPoint2D 数组。
  4. 基于 CurveFunction() 指针和三个数值来构建函数参数: 初始, 最终和增量参数。

方法 CurveAdd() 返回 CCurve 类的指针, 可供快速访问最新创建的曲线并可改变其属性。

   double x[]={-10,-4,-1,2,3,4,5,6,7,8};

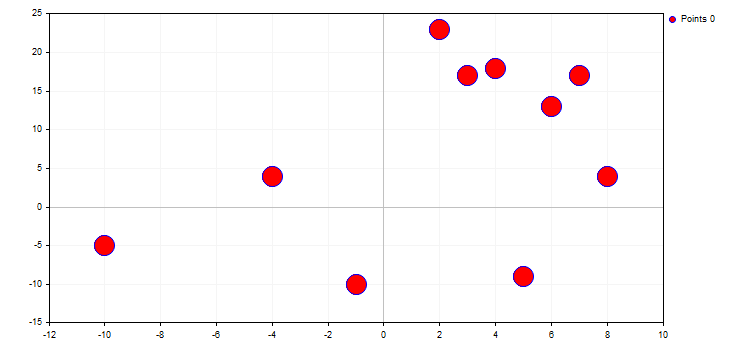
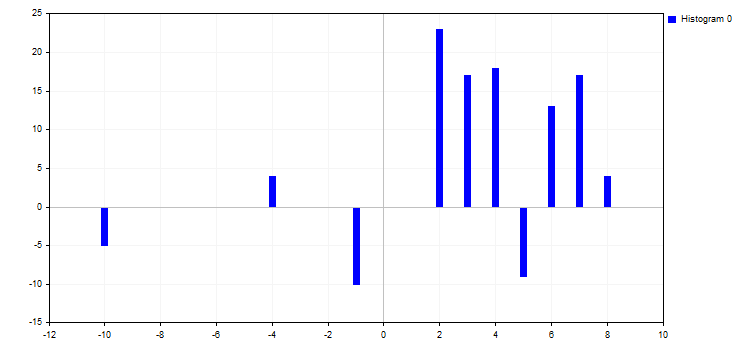
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};

   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);

3. 所有添加的曲线随后可显示在图表上。这可以通过三种方式完成。

  1. 通过使用 CurvePlotAll() 方法自动绘制加入图表的所有曲线。
    graphic.CurvePlotAll();
  2. 通过使用 CurvePlot() 方法按照指定索引绘制一条曲线。
    graphic.CurvePlot(0);
  3. 通过使用 Redraw() 方法并设置曲线的可视属性为 'true'。
    curve.Visible(true);
    graphic.Redraw();

4. 为了在图表上绘制图形, 调用 Update() 方法。结果就是, 我们得到了绘制简单图形脚本的整个代码:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| 脚本的 start 函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"图形",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   graphic.CurvePlotAll();
   graphic.Update();
  }

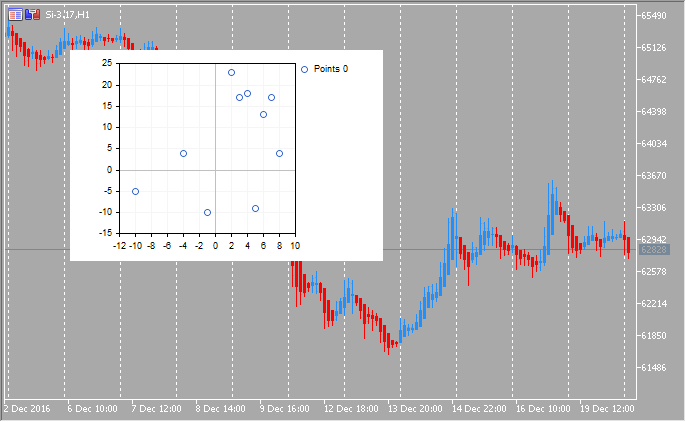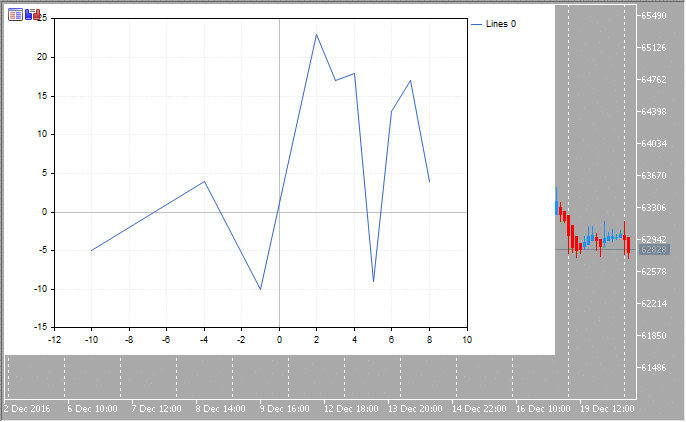
以下是效果图:


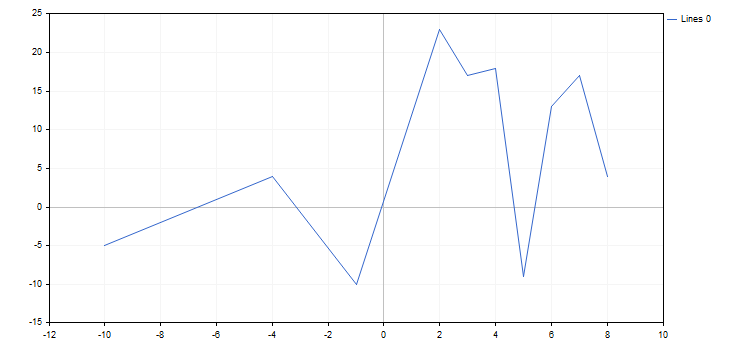
图形属性及其所有功能可随时更改。例如, 我们可以向图形坐标轴添加标签, 修改曲线的名称并启用条形近似模式:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| 脚本的 start 函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"图形",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   curve.Name("示例");                
   curve.LinesIsSmooth(true);            
   graphic.XAxis().Name("X - 轴");      
   graphic.XAxis().NameSize(12);          
   graphic.YAxis().Name("Y - 轴");      
   graphic.YAxis().NameSize(12);
   graphic.YAxis().ValuesWidth(15);
   graphic.CurvePlotAll();
   graphic.Update();
   DebugBreak();
  }


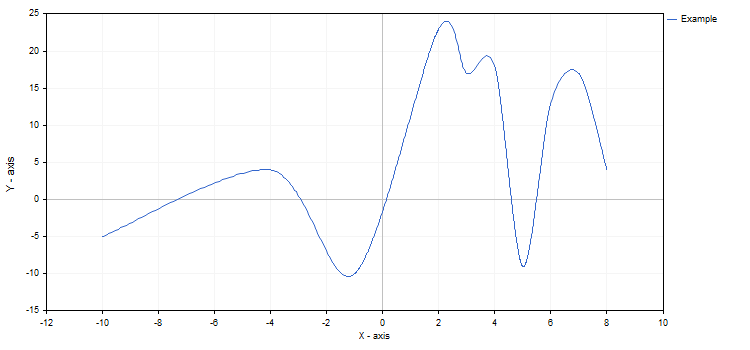
如果在调用 CurvePlotAll 之后更改了设置, 我们将不得不另行调用 Redraw 方法来刷新它们。

就像许多现代函数库一样, Graphics 包含各种现成的算法, 大大简化了图表绘图:

  1. 如果没有明确指定, 函数库会自动生成曲线的对比色。
  2. 图形坐标轴具有参数化自动缩放模式, 如果需要可以禁用。
  3. 曲线名称根据其类型和添加顺序自动生成。
  4. 图形的工作区域自动排列, 并设置实际的坐标轴。
  5. 使用线条时能够平滑曲线。

图形库还有一些额外的方法可用于向图表添加新元素:

  1. TextAdd() — 在图表上的任意位置添加一个文本。坐标应按照实际数值设定。使用 FontSet 方法精确配置显示文本。
  2. LineAdd() — 在图表上的任意位置添加一条线。坐标应按照实际数值设定。
  3. MarksToAxisAdd() — 在指定的坐标轴上添加新标签。

所添加元素的数据不会在任何地方保存。在图表上绘制新曲线或重绘之前元素之后, 它们会消失。


图形类型

图形库支持曲线绘制的基本类型。所有这些均在 ENUM_CURVE_TYPE 枚举中指定:

  1. CURVE_POINTS — 绘制虚线
  2. CURVE_LINES — 绘制一条实线
  3. CURVE_POINTS_AND_LINES — 绘制点划线
  4. CURVE_STEPS — 绘制阶梯曲线
  5. CURVE_HISTOGRAM — 绘制直方图曲线
  6. CURVE_NONE — 无需画线

这些模式中的每一种都有自己的属性, 可影响曲线在图表上的显示。指向曲线的 CCurve 指针可迅速修改这些属性。因此, 建议保留 CurveAdd 方法返回的所有指针。属性名称始终以所用曲线绘图模式开头。

我们来更详尽地观察每种类型的属性。

1. CURVE_POINTS 是最快速和简单的类型。每个曲线坐标依照指定属性显示为一个点:

  • PointsSize — 点的大小
  • PointsFill — 是否填充的标志
  • PointsColor — 填充颜色
  • PointsType — 点的类型

在此情况下, 曲线本身的颜色定义了点边界的颜色。

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_POINTS);
   curve.PointsSize(20);
   curve.PointsFill(true);
   curve.PointsColor(ColorToARGB(clrRed,255));

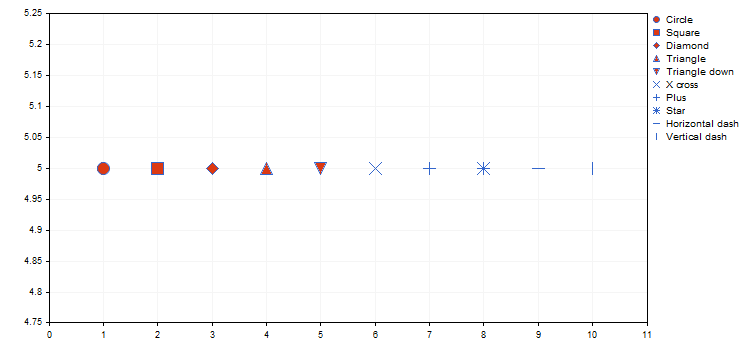
点的类型来自 ENUM_POINT_TYPE 枚举定义的某种几何形状。该形状用于显示所有曲线的点。ENUM_POINT_TYPE 总共包含十个主要几何形状:

  1. POINT_CIRCLE — 圆形 (作为省缺)
  2. POINT_SQUARE — 正方形
  3. POINT_DIAMOND — 菱形
  4. POINT_TRIANGLE — 三角形
  5. POINT_TRIANGLE_DOWN — 倒三角形
  6. POINT_X_CROSS — 叉字
  7. POINT_PLUS — 加号
  8. POINT_STAR — 星形
  9. POINT_HORIZONTAL_DASH — 横线
  10. POINT_VERTICAL_DASH — 竖线

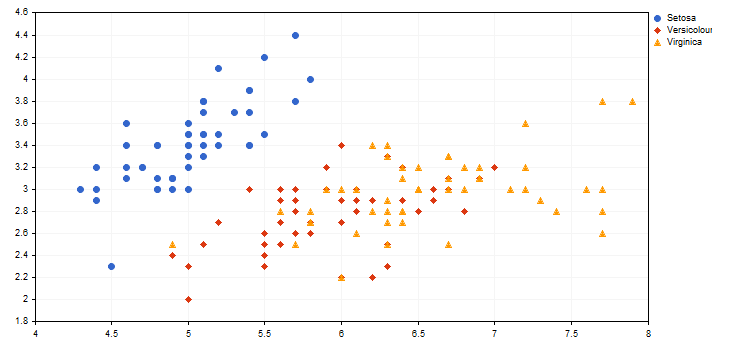
以下不同类型虹膜的直观表现的示例来自附带的 IrisSample.mq5 脚本中 (参见文章 "使用 MetaTrader 5 中的自组织特征映射 (Kohonen 映射)")。



2. CURVE_LINES 显示模式是用于可视化曲线的主要模式, 其中每一对点连接一条或多条 (在平滑的情况下) 直线。模式属性如下:

  • LinesStyle — 线形来自 ENUM_LINE_STYLE 枚举
  • LinesSmooth — 是否应执行平滑的指示标志
  • LinesSmoothTension — 平滑深度
  • LinesSmoothStep — 平滑时的近似线的长度

图形具有标准参数化曲线平滑算法。它由两个阶段组成:

  1. 在其派生词的基础上, 每一对点由两个参考点定义
  2. 一条指定近似步长的 贝塞尔曲线 基于这四个点绘制

LinesSmoothTension 参数取值范围 (0.0; 1.0]。如果 LinesSmoothTension 设为 0.0, 不会发生平滑。通过增加这个参数, 我们得到越来越平滑的曲线。

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_LINES);
   curve.LinesStyle(STYLE_DOT);
   curve.LinesSmooth(true);
   curve.LinesSmoothTension(0.8);
   curve.LinesSmoothStep(0.2);


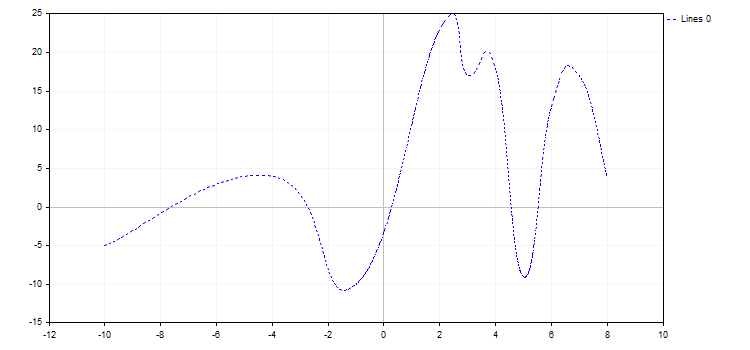
3. CURVE_POINTS_AND_LINES 结合了前两种显示模式及其属性。

4. 在 CURVE_STEPS 模式中, 每一对点连接两条线作为一个台阶。该模式有两个属性:

  • LinesStyle — 该属性取自 CURVE_POINTS, 并定义了线条样式
  • StepsDimension — 台阶维度: 0 — x (一条水平线后跟一条垂直线) 或者 1 — y (一条垂直线后跟一条水平线)。
   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_STEPS);
   curve.LinesStyle(STYLE_DASH);
   curve.StepsDimension(1);

5. 模式 CURVE_HISTOGRAM 绘制一根标准柱线直方图。该模式具有单个属性:

  • HistogramWidth — 柱线宽度

如果该值太大, 则柱线也许重叠, 并且 Y 值较大的柱线 "吞噬" 具有较小值的相邻柱线。

6. 模式 CURVE_NONE 则无论曲线可视与否均禁用其图形呈现。

当自动缩放时, 所有添加到图表的曲线均有确定的数值。因此, 即使不绘制曲线, 或者设置为 CURVE_NONE 模式, 仍然考虑其数值。


图形函数 — 在几行内快速生成

函数库的另一个优点是可协同 CurveFunction 函数指针工作。在 MQL5 里, 函数指针只接受全局或静态函数, 而函数语法应完全与指针对应。在我们例子中, CurveFunction 配置为函数接收双精度类型参数。

为了通过一个函数指针来构建一条曲线, 我们需要准确地设定初始 (从) 和最终 (至) 参数, 以及增量 (步长)。增量越小, 我们需要构建越多的函数指针。为了创建数据序列, 使用 CurveAdd(), 而绘制函数时采用 CurvePlot() 或 CurvePlotAll()。

例如, 我们来创建一条抛物线函数并用各种增量来绘制它:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| 抛物线                                                            |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| 脚本的 start 函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from1=-5;
   double to1=0;
   double step1=1;
  
   double from2=0;
   double to2=5;
   double step2=0.2;
  
   CurveFunction function = Parabola;
  
   CGraphic graph;
   graph.Create(0,"Graph",0,30,30,780,380);
   graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
   graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
   graph.CurvePlotAll();
   graph.Update();
  }

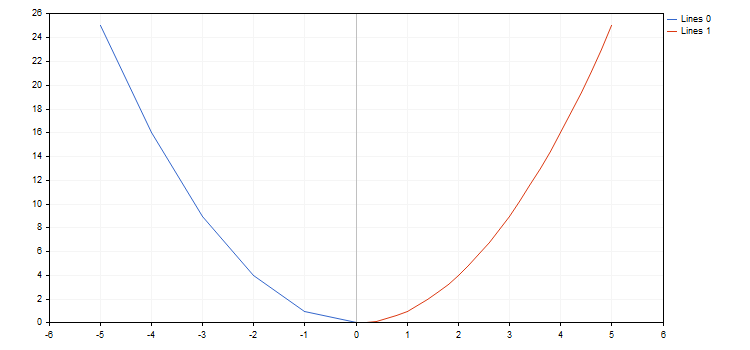
函数库可协同具有断点 (坐标之一为正负无穷, 或非数字) 的函数操作。函数增量应予以考虑, 因为有时候, 我们可能轻易地错过一个断点。在此情况下, 图形不符合预期。例如, 我们来绘制两条双曲线函数, 取值范围 [-5.0; 5.0], 第一个函数步长为 0.7, 第二个 — 0.1。结果显示如下:

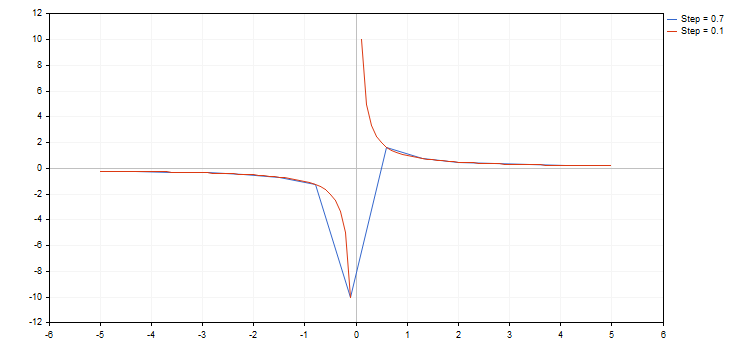
正如我们在上图中所见, 当使用 0.7 步长时, 我们简单地忽略了一个断点。结果就是, 结果曲线的真实双曲线函数几乎什么也没做。

当使用函数时, 也许会发生除零错误。有两种方式来处理这个问题:

  • 在 metaeditor.ini 里禁用除零检查
    [Experts]
    FpNoZeroCheckOnDivision=1
  • 或分析函数中使用的方程并返回这种实例的有效值。使用宏来处理的示例可在附带的 3Functions.mq5 和 bat.mq5 文件里找到。






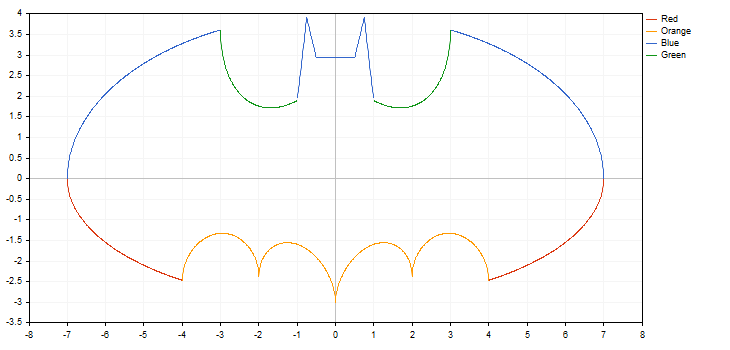
快速绘制函数

图形库还包括一定数量的 GraphPlot()全局函数, 基于可用数据执行所有图形绘制, 并返回图表上的一个对象名称作为结果。这些函数类似于 R 或 Python 语言的 'plot (绘图)', 可令您立即直观不同格式的数据。

函数 GraphPlot 有 10 种不同重载可令您在单一图表上绘制不同的曲线, 并以不同方式设置它们。所有您需要做的只是使用一种可用方法绘制曲线的表单数据。例如, 用于快速绘制 x[] 和 y[] 数组的源代码如下所示:

void OnStart()
  {
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   GraphPlot(x,y);
  }

它看起来类似于 R:

> x<-c(-10,-4,-1,2,3,4,5,6,7,8)
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)

利用 MQL5 上的 GraphPlot 函数与 R 上的绘图函数构建的三种主要显示模式的比较结果图:

1. 点状曲线


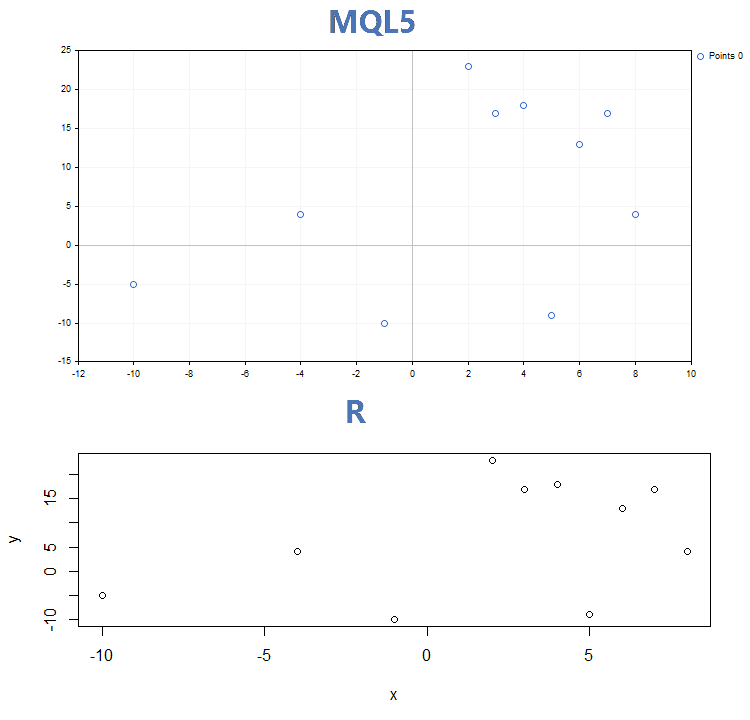
2. 线条


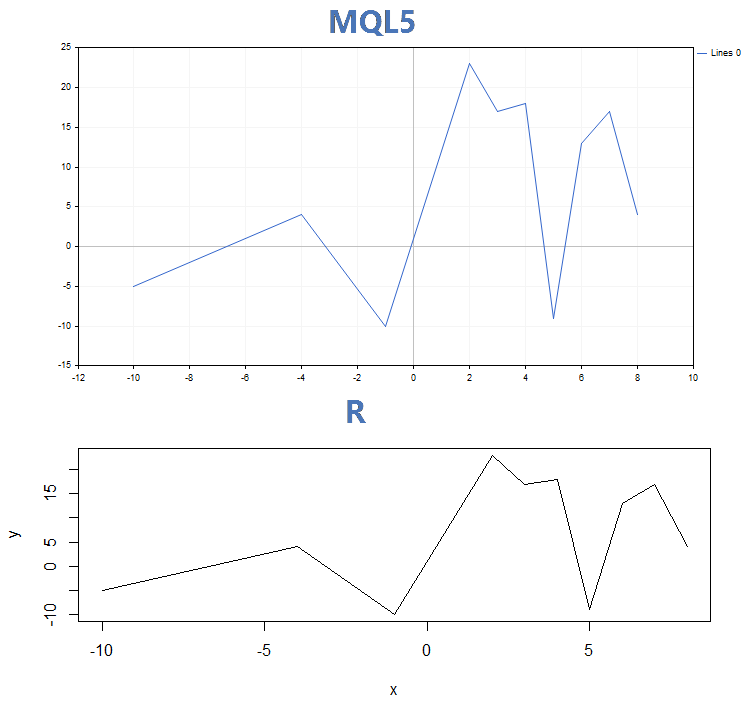
3. 直方图


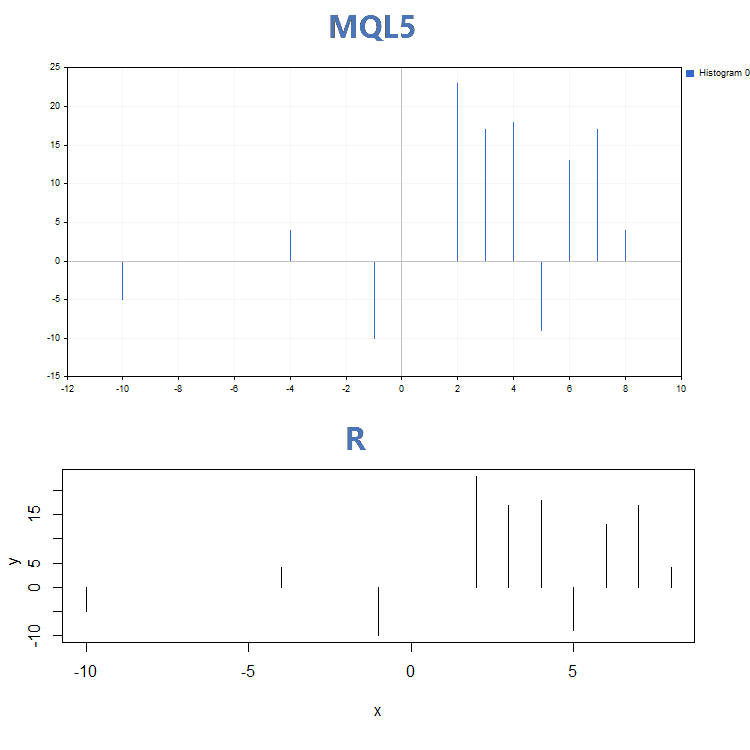
除了 GraphPlot() 和 plot() 函数操作上的观感显著不同之外, 它们还有不同的输入参数。函数 plot() 允许设置特定的曲线参数 (例如, 'lwd' 来更改线宽), 但 GraphPlot() 函数只包含构建数据所需的关键参数。

我们来为它们命名:

  1. 曲线数据是上述 四种格式 之一。
  2. 绘制类型 (省缺是 CURVE_POINTS)。
  3. 对象名称 (省缺是 NULL)。

每个采用图形库创建的图形均由图表对象和一个分配给它的图形资源组成。图形资源名称是在对象名基础上简单地添加前缀 "::" 形成。例如, 如果对象名称为 "SomeGraphic", 则其图形资源名称为 "::SomeGraphic"。

函数 GraphPlot() 在图表上有一个固定的锚点 x=65 和 y=45。图形宽度和高度依据图表大小计算: 宽为图表宽度的 60％, 而高度是图表高度的 65％。因此, 若当前图表维度小于 65 到 45, 则 GraphPlot() 函数无法正常工作。

如果在创建图形时应用一个已创建对象的名称, 则图形库会在检查其资源类型后尝试在该对象上显示图形。如果资源类型是 OBJ_BITMAP_LABEL, 在相同的对象 - 资源配对上执行绘图。

如果将对象名称显式传递给 GraphPlot() 函数, 则尝试查找该对象, 并在其上显示图形。如果对象未发现, 则会根据指定的名称自动创建一个新的对象-资源配对。当使用 GraphPlot() 函数时未明确指定对象名称, 使用 "Graphic" 标准名称。 

在此情况下, 您可以指定图形锚点及其大小。为达此目的, 创建一个具有必要参数的对象-资源配对, 并将创建的对象名称传递给 GraphPlot() 函数。通过 Graphic 对象名称创建个配对, 我们重新定义并固化了 GraphPlot 函数的标准画布, 消除了每次调用时传递对象名称的必要性。

例如, 我们从上面的例子中获取数据, 并设置一个大小为 750х350 的新图形。此外, 我们将 锚点 移至左上角:

void OnStart()
  {
//--- 在图表上创建对象和动态资源
   string name="Graphic";
   long x=0;
   long y=0;
   int width=750;
   int height=350;
   int data[];
   ArrayResize(data,width*height);
   ZeroMemory(data);
   ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
   ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
   ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
   ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
   ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- 创建 x 和 y 数组
   double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- 绘制 x 和 y 数组
   GraphPlot(arr_x,arr_y,CURVE_LINES);
  }



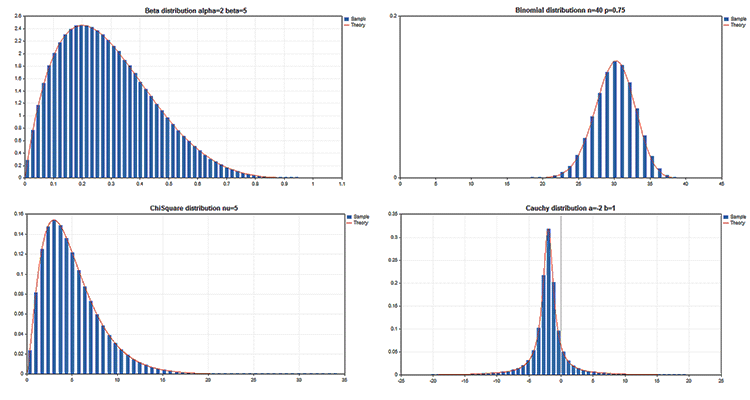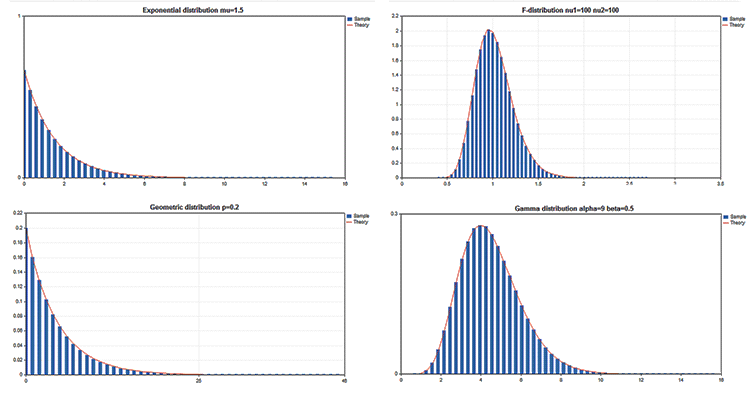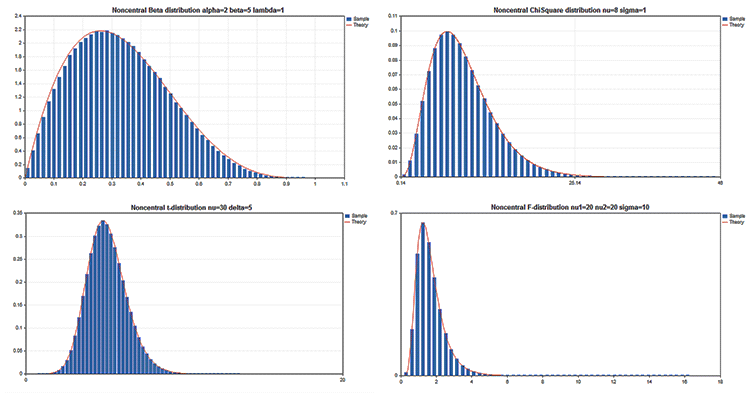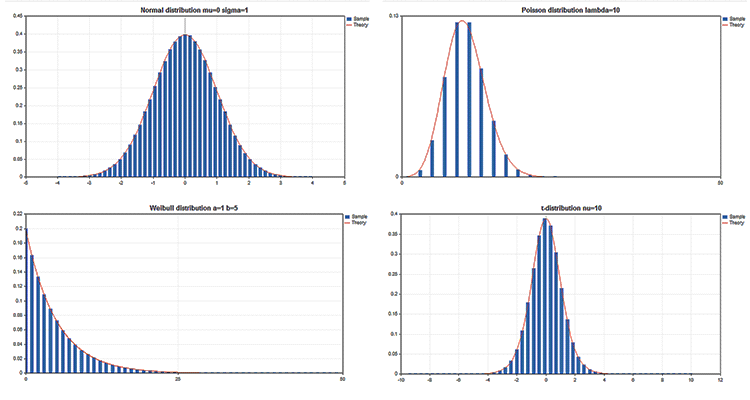
科学图样

标准库包括的 统计 部分功能, 可运用概率理论处理多个 统计分布。每个分发都附有一个样本图和一个代码来检索它。在此, 我们只需在单个 GIF 中显示这些图片。示例的源代码附代在 MQL5.zip 文件中。将它们解压缩到 MQL5\Scripts 中。

所有这些示例的价格图表通过 CHART_SHOW 属性禁用:

//--- 禁用价格图表
   ChartSetInteger(0,CHART_SHOW,false);

这允许我们将图表窗口转换为单一的大型 画板, 并绘制任何复杂的应用了图形资源 的对象。

参阅文章 "为莫斯科交易所期货市场开发扩散策略的一个示例", 文中展示了应用 图形库 来显示训练样本, 以及通过 Alglib 函数库得到的线性回归结果。


图形库的主要优点

MQL5 语言不仅允许开发人员创建交易机器人和技术指标, 还可以使用 ALGLIB, 模糊 和 统计 函数库。 所获数据可随后通过提供的图形库轻松地可视化。大多数操作都是自动的, 而且函数库提供了广泛的函数:

  • 5 种图形 显示类型
  • 10 种图表 行情类型
  • 自动依照 X 和 Y 轴缩放图表
  • 颜色自动选择, 即使图表具有若干个结构
  • 使用标准抗锯齿技术或更先进的 Bresenham 算法 进行线条平滑
  • 能够设置 条形近似 参数来显示线条
  • 有能力基于 x[] 和 y[] 数组在单行代码内绘制图形
  • 有能力使用函数指针绘制图形

图形库简化了科学图形绘制, 并将交易应用程序的开发提升到一个新的水平。MetaTrader 5 平台允许您按照专业的方式直接在终端窗口中执行任何复杂的数学计算并显示结果。

尝试附代的代码。您不再需要第三方发布包了！



       

全部回复

0/140

量化课程

    移动端课程