内容

• 概述
• 1. 创建特征
• 1.1. 特征变换
• 1.1.1. 变换
• 1.1.2. 常规化
• 1.1.3. 离散
• 1.2. 创建新特征
• 2. 选择预测因子
• 2.1. 直观评估
• 2.2. 分析评估
• 2.3. 神经网络
• 结束语
• 应用

概述

在 之前的 文章中, 我们研究了输入数据的获取和准备, 以及目标变量的不同方面。若要得到第一篇文章中的脚本, 您需要实现第一部分的所有脚本, 或从 RStudio 应用程序的第一部分下载计算结果。

1. 创建特征

创建特征是一门从手中的数据当中获取附加信息的科学 (和艺术)。我们的目标不是添加新的数据, 而是利用我们已经拥有的数据。新的能力令我们能够获得数据样本的新特征。这些特征使得训练数据集合更加精确的标注, 表征和划分。这可提供额外的精度。

这个过程可以分为两个阶段:

• 变换. 根据场景, 这可以是四种转换类型之一: 常规化数据, 去除变量偏度, 去除异常值和离散化。
• 创建特征. 从现有的变量中提取新变量称为创建一个新特征。这可以揭示数据集合中的隐藏关系。

1.1. 特征变换

1.1.1. 变换

什么是变量的变换？

在数据建模中, 变换是通过变量的函数替换变量。举例来说, 这可通过平方或立方根或对数来更改 x 变量。换言之, 变换是一个改变变量分布, 以及此变量与其它变量关系的过程。

我们来回忆一下何时变量的变换是有用的。

• 当我们想要改变一个变量的标度, 或将其数值标准化以便更好的理解。如果不同的数据具有不同的标度, 则需要进行此转换。这不会导致分布形状的变化。


• 当必须将变量之间复杂的非线性和曲线关系转化为线性关系时。这更加生动, 并提供更好的预测能力。在这种情况下, 可以使用散点图找出两个连续变量之间的关系。在这种情况下通常使用对数变换。


• 当一个非对称分布需要改变成一个对称分布, 以便更简单的解释和分析。一些建模方法需要变量的正态分布。因此, 当我们处理非均匀分布时, 我们可以使用变换来降低偏度。对于偏斜分布, 我们取一个变量的平方或立方根或对数, 而左偏斜分布利用平方/立方或使用指数函数进行平滑。


• 当一个连续变量需要转换为离散变量时。这种变换的方法是离散化。

一般的变换方法是什么？

有多种用来变换变量的方法。我们已经提到了它们中的一些: 平方和立方根, 对数, 三角函数和切分。我们来深入研究一些方法, 并确定其优点和缺点。

1. 取对数。这是用来改变变量分布形状的常用变换方法。通常用于降低右偏度。此功能不适用于零值和负值。
   


2. 平方/立方根. 该函数对变量的分布有很大的影响, 尽管不如采用对数那么强大。立方根的优点是它可以用于零值和负值。平方根只能取正值和零。


3. 离散/分箱. 这用于数值分类。离散化适用于原始数据, 百分数和频率。分类方法的选择是基于数据的性质。我们可以对相互依赖的变量进行联合分割。

任何数据变换都会导致分布的变化。为了描绘这一点, 我们将使用两种变换方法的例子。

我们的初始数据集合的两个问题是异常值和右偏度。我们已有 研究过的 去除异常值的方法。现在, 我们先尝试删除/减少非对称, 然后删除异常值。

方法 1。

为了消除 x 数据集合的强右偏差, 我们取底为 2 的对数, 然后消除异常值。由于初始数据集合中的变量值远小于 1, 且它们之间存在负值, 所以我们将取每个变量加 1 的对数来提高准确度。我们看看曲线会发生什么变化。

evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
       sk.ln <- skewness(x.ln)},
      env)
 > env$sk.ln
               ftlm      stlm      rbci      pcci   v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
          v.satl   v.rftl     v.rstl    v.ftlm     v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
            v.pcci
Skewness 0.1811206

三个变量 — stlm, rbci 和 v.ftlm 有明显的左偏度。v.fatl, v.satl 和 v.rftl 变量仍然偏向右侧。其它变量的偏度已趋于平缓。我们从这个数据集合中删除并插补异常值, 然后再看变量的偏度和分布:

evalq({
  foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
    remove_outliers(x.ln[ ,i])
  } -> x.ln.out
  colnames(x.ln.out) <- colnames(x.ln)
  },  
env)
evalq({
  foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
    capping_outliers(x.ln[ ,i])
  } -> x.ln.cap
  colnames(x.ln.cap) <- colnames(x.ln)
},  
env)
evalq({
  sk.ln.out <- skewness(x.ln.out) 
  sk.ln.cap <- skewness(x.ln.cap)
}, 
env)
> env$sk.ln.out
              ftlm       stlm       rbci        pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
              v.fatl      v.satl      v.rftl     v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
              v.ftlm      v.stlm      v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
               ftlm       stlm       rbci        pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
              v.fatl      v.satl     v.rftl     v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
              v.ftlm      v.stlm      v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243

两个数据集合 (x.out 和 x.cap) 中的数据几乎是对称的。分布如下图所示。

par(mfrow = c(2,2))
boxplot(env$x.ln, 
              main = "x.ln with outliers",
              xlab = "")
boxplot(env$x.ln.out, 
              main = "x.ln.out without outliers",
              xlab = "")
boxplot(env$x.ln.cap, 
              main = "x.ln.cap with imputed outliers",
              xlab = "")
par(mfrow = c(1,1))

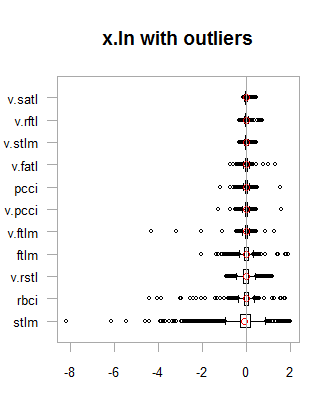
图例.1. 含/不含异常值的对数变换数据

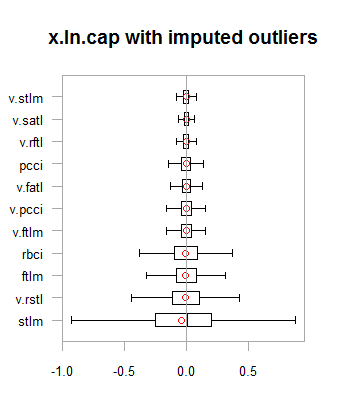
图例.2. 含异常值插补的对数变换数据

结果与以前的变换非常相似, 但有一点例外。变量的变化范围已经变得越来越宽。

我们来变换 x.ln.cap 数据帧, 并查看集合的变化和协变:

 evalq(x.ln.cap %>% tbl_df() %>% 
        cbind(Data = dataSetClean$Data, .,
              Class = dataSetClean$Class) -> 
        dataSetLnCap, 
      env) 

绘制图表:

require(GGally)
evalq(ggpairs(dataSetLnCap, columns = 2:7, 
              mapping = aes(color = Class),
              title = "PredLnCap1"), 
      env)
evalq(ggpairs(dataSetLnCap, columns = 8:13, 
              mapping = aes(color = Class),
              title = "PredLnCap2"), 
      env)

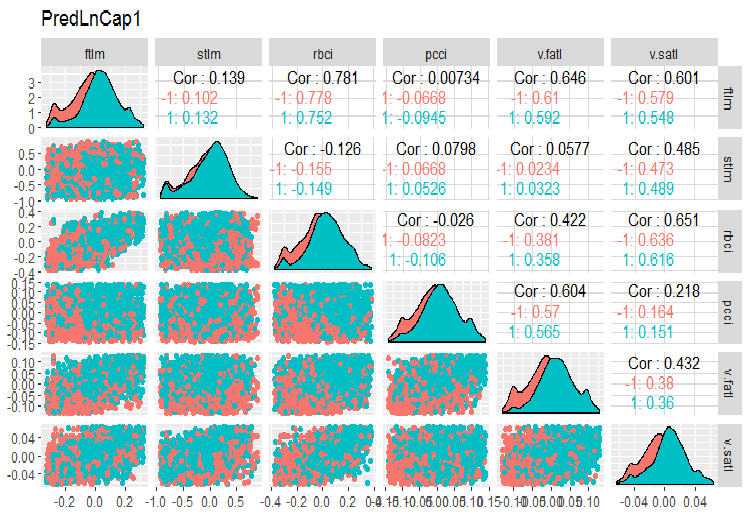
图例.3. 对数变换数据的参数, 第 1 部分

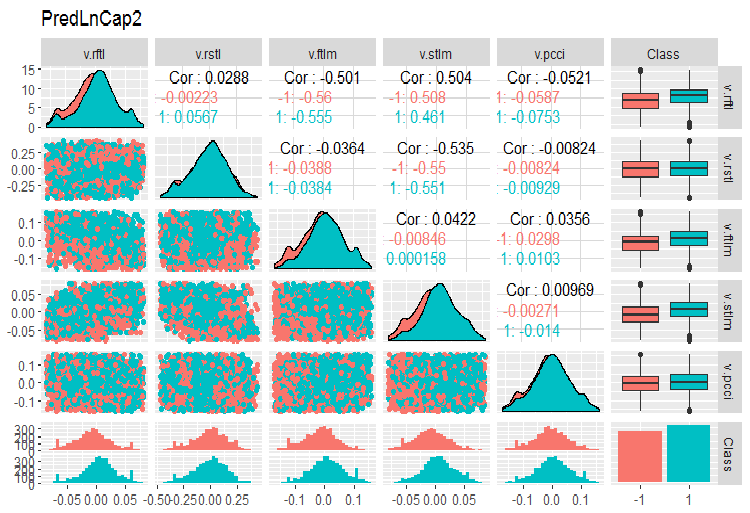
图例. 4. 对数变换数据的参数, 第 2 部分

方法 2. 

使用 sin(2*pi*x) 函数变换数据, 消除和插补异常值, 然后评估图表上的偏差, 异常值分布和变换变量协变。

evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
      sk.sin <- skewness(x.sin)
      },
env)
#----------
evalq({
  foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
    remove_outliers(x.sin[ ,i])
  } -> x.sin.out
  colnames(x.sin.out) <- colnames(x.sin)
},  
env)
#-----------------
evalq({
  foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
    capping_outliers(x.sin[ ,i])
  } -> x.sin.cap
  colnames(x.sin.cap) <- colnames(x.sin)
},  
env)
#-----------
evalq({
  sk.sin.out <- skewness(x.sin.out) 
  sk.sin.cap <- skewness(x.sin.cap)
}, 
env) 

这些变换数据集合的偏度是多少？

env$sk.sin
                ftlm        stlm        rbci         pcci
Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463
             v.fatl    v.satl     v.rftl      v.rstl
Skewness 0.03280465 0.5217757 0.05611136 -0.02825112
             v.ftlm     v.stlm     v.pcci
Skewness 0.04923953 -0.2123434 0.01738377
> env$sk.sin.out
                ftlm        stlm        rbci       pcci
Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892
             v.fatl      v.satl      v.rftl      v.rstl
Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112
               v.ftlm     v.stlm       v.pcci
Skewness 0.0009366441 0.01835948 0.0008843329
> env$sk.sin.cap
                ftlm        stlm        rbci       pcci
Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132
              v.fatl      v.satl      v.rftl      v.rstl
Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112
              v.ftlm      v.stlm      v.pcci
Skewness 0.007003051 0.009237835 0.002101687

如您所见, 这种变换可令所有的数据集合对称。我们看看这些集合的样子:

par(mfrow = c(2, 2))
boxplot(env$x.sin, main = "x.sin with outlier")
abline(h = 0, col = 2)
boxplot(env$x.sin.out, main = "x.sin.out without outlier")
abline(h = 0, col = 2)
boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier")
abline(h = 0, col = 2)
par(mfrow = c(1, 1))

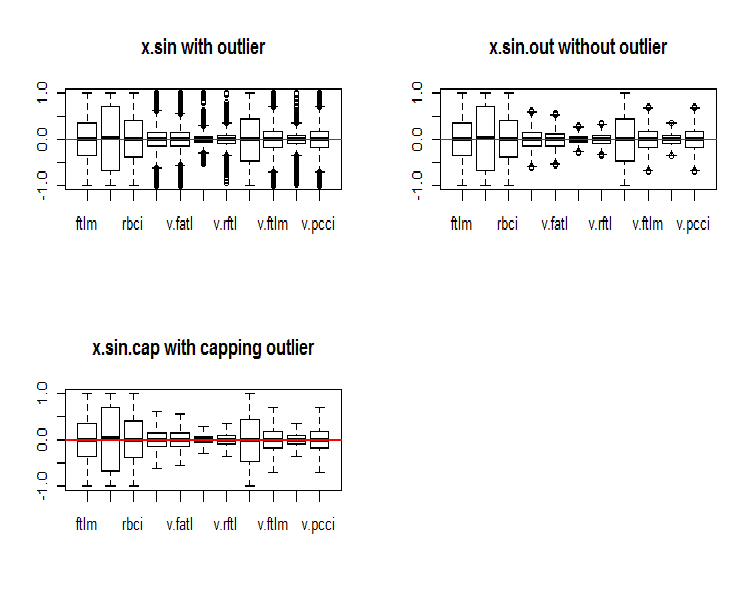
图例.5. 通过 sine() 函数变换的数据集合

乍看起来, 这些数据集合看起来比以前的数据 (初始和转换的数据集合) 更好。

现在, 我们想要看看异常值被删除之后变量中的 NA 分布。

require(VIM)
evalq(a <- aggr(x.sin.out), env)

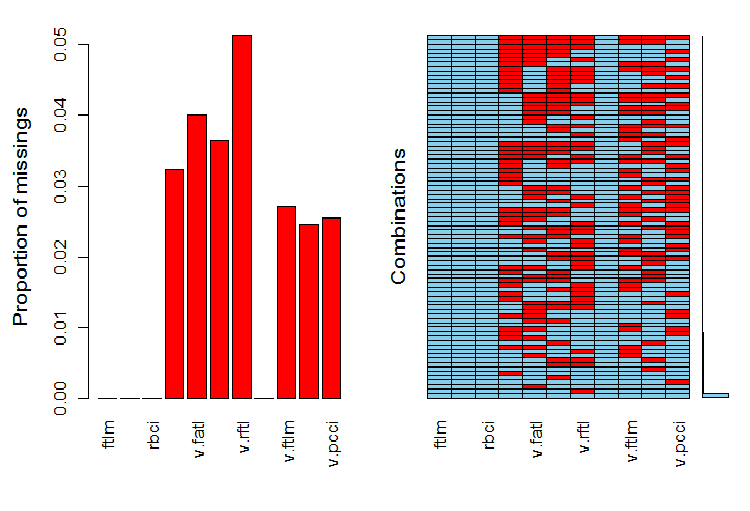
图例.6. 在数据集合中的 NA 分布

图表的左侧部分显示每个变量中未定义数据的相对数量。右侧显示不同数量的 NA (从底部到顶部递增) 的示例组合。我们可以看到数值:

> print(env$a)

 Missings in variables:
 Variable Count
     pcci   256
   v.fatl   317
   v.satl   289
   v.rftl   406
   v.ftlm   215
   v.stlm   194
   v.pcci   201

在变量中 NA 的分布是什么？

 par(mfrow = c(3, 4))
evalq(
  foreach(i = 1:ncol(x.sin.out)) %do% {
    barMiss(x.sin.out, pos = i, only.miss = TRUE, 
            main = "x.sin.out without outlier")
  }, env
)
par(mfrow = c(1, 1))

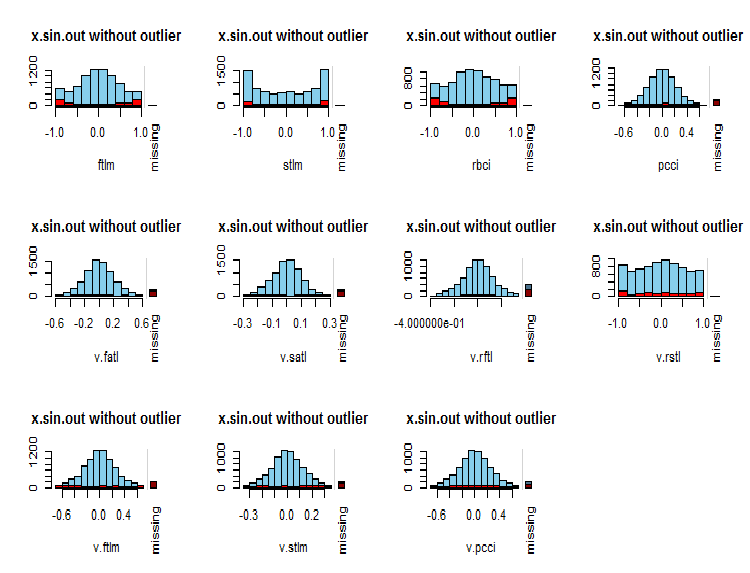
图例.7. 变量中的 NA 分布

变量的观测值显示为蓝色, 其它变量在当前变量不同数值范围内的 NA 数量以红色显示。右侧柱线表示当前变量对所有变量的 NA 总数的贡献。

最后, 我们来看看含有插补异常值的变换数据集合的变异和协变。

#---------------
evalq(x.sin.cap %>% tbl_df() %>% 
        cbind(Data = dataSetClean$Data, .,
              Class = dataSetClean$Class) -> 
        dataSetSinCap, 
      env) 
require(GGally)
evalq(ggpairs(dataSetSinCap, columns = 2:7, 
              mapping = aes(color = Class),
              title = "dataSetSinCap1 with capping outlier "), 
      env)
evalq(ggpairs(dataSetSinCap, columns = 8:13, 
              mapping = aes(color = Class),
              title = "dataSetSinCap2 with capping outlier"), 
      env)
#---------------------------

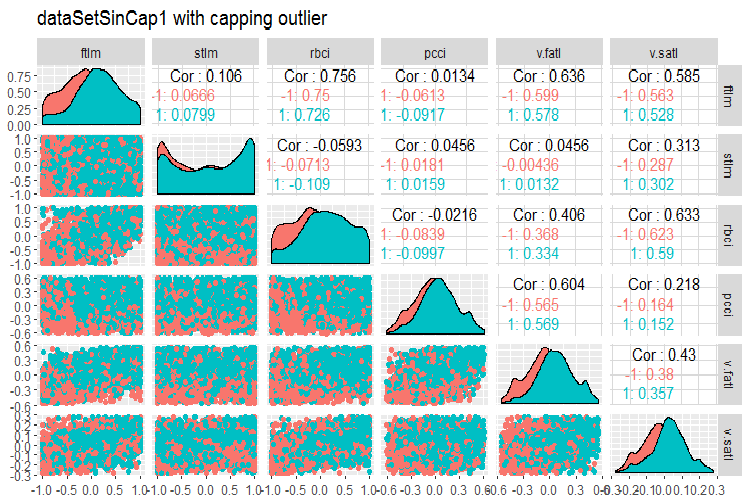
图例.8. sin()-变换数据的参数, 第 1 部分

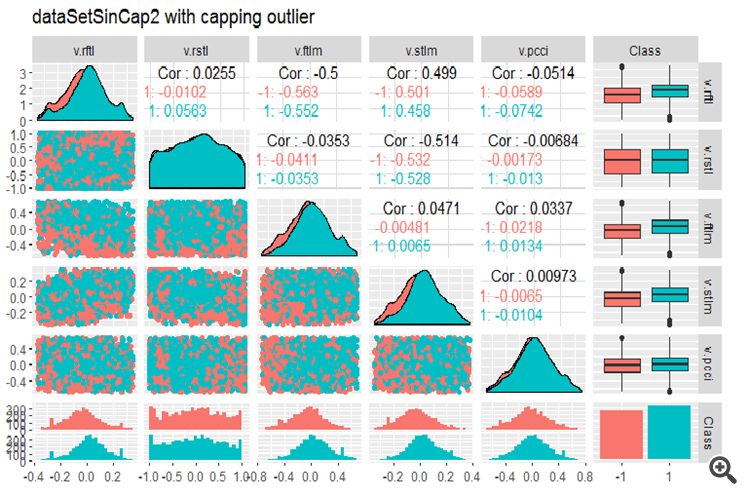
图例.9. sin()-变换数据的参数, 第 2 部分

1.1.2. 常规化

我们正在为神经网络准备数据, 因此变量必须在 { -1..+1 } 的范围内。为此, 将使用 preProcess()::caret 函数, 参数为 method = “spatialSign”。备用方案, 在常规化之前将数据居中或缩放。这是一个非常简单的过程, 我们不会在本文中多叙。

有一件事要记住。从训练数据集合获得的常规化参数 将用于测试和集合验证。

为了进一步利用我们先前计算中获得的数据集合 (dataSet 未去除高度相关数值), 我们将 训练/测试/验证 切分并把它们带进范围 (-1,+1) 而无需标准化。

用标准化执行常规化, 请记住, 当定义常规化参数 (平均值/中值, sd/mad) 时, 也要定义插补异常值的参数。将来, 它们将被用于 训练/测试/验证。在本文前面我们编写了两个函数: prep.outlier() 和 treatOutlier()。它们即是为此目的而设计的。

操作顺序:

1. 在 训练 中定义异常值参数
2. 从 训练 中删除异常值。
3. 在 训练 中定义标准化参数
4. 在 训练/测试/验证 中插补异常值
5. 常规化 训练/测试/验证。

我们不会研究这个变体。你可自行学习。

将数据切分至 训练/测试/验证:

 evalq(
{
  train = 1:2000
  val = 2001:3000
  test = 3001:4000
  DT <- list()
  list(clean = data.frame(dataSet) %>% na.omit(), 
       train = clean[train, ], 
       val = clean[val, ], 
       test = clean[test, ]) -> DT
}, env) 

定义 训练 集合的常规化参数, 并在 训练/验证/测试 中常规化异常值:

 require(foreach)
evalq(
{
 preProcess(DT$train, method = "spatialSign") -> preproc 
 list(train = predict(preproc, DT$train), 
        val = predict(preproc, DT$val),
        test = predict(preproc, DT$test)
       ) -> DTn
}, 
env) 

我们来看看 训练 集合的总体统计:

 > table.Stats(env$DTn$train %>% tk_xts())
Using column `Data` for date_var.
                     ftlm      stlm      rbci      pcci
Observations    2000.0000 2000.0000 2000.0000 2000.0000
NAs                0.0000    0.0000    0.0000    0.0000
Minimum           -0.5909   -0.7624   -0.6114   -0.8086
Quartile 1        -0.2054   -0.2157   -0.2203   -0.2110
Median             0.0145    0.0246    0.0147    0.0068
Arithmetic Mean    0.0070    0.0190    0.0085    0.0028
Geometric Mean    -0.0316   -0.0396   -0.0332   -0.0438
Quartile 3         0.2139    0.2462    0.2341    0.2277
Maximum            0.6314    0.8047    0.7573    0.7539
SE Mean            0.0060    0.0073    0.0063    0.0065
LCL Mean (0.95)   -0.0047    0.0047   -0.0037   -0.0100
UCL Mean (0.95)    0.0188    0.0333    0.0208    0.0155
Variance           0.0719    0.1058    0.0784    0.0848
Stdev              0.2682    0.3252    0.2800    0.2912
Skewness          -0.0762   -0.0221   -0.0169   -0.0272
Kurtosis          -0.8759   -0.6688   -0.8782   -0.7090
                   v.fatl    v.satl    v.rftl    v.rstl
Observations    2000.0000 2000.0000 2000.0000 2000.0000
NAs                0.0000    0.0000    0.0000    0.0000
Minimum           -0.5160   -0.5943   -0.6037   -0.7591
Quartile 1        -0.2134   -0.2195   -0.1988   -0.2321
Median             0.0015    0.0301    0.0230    0.0277
Arithmetic Mean    0.0032    0.0151    0.0118    0.0177
Geometric Mean    -0.0323   -0.0267   -0.0289   -0.0429
Quartile 3         0.2210    0.2467    0.2233    0.2657
Maximum            0.5093    0.5893    0.6714    0.7346
SE Mean            0.0058    0.0063    0.0062    0.0074
LCL Mean (0.95)   -0.0082    0.0028   -0.0003    0.0033
UCL Mean (0.95)    0.0146    0.0274    0.0238    0.0321
Variance           0.0675    0.0783    0.0757    0.1083
Stdev              0.2599    0.2798    0.2751    0.3291
Skewness          -0.0119   -0.0956   -0.0648   -0.0562
Kurtosis          -1.0788   -1.0359   -0.7957   -0.7275
                   v.ftlm    v.stlm    v.rbci    v.pcci
Observations    2000.0000 2000.0000 2000.0000 2000.0000
NAs                0.0000    0.0000    0.0000    0.0000
Minimum           -0.5627   -0.6279   -0.5925   -0.7860
Quartile 1        -0.2215   -0.2363   -0.2245   -0.2256
Median            -0.0018    0.0092   -0.0015   -0.0054
Arithmetic Mean   -0.0037    0.0036   -0.0037    0.0013
Geometric Mean    -0.0426   -0.0411   -0.0433   -0.0537
Quartile 3         0.2165    0.2372    0.2180    0.2276
Maximum            0.5577    0.6322    0.5740    0.9051
SE Mean            0.0061    0.0065    0.0061    0.0070
LCL Mean (0.95)   -0.0155   -0.0091   -0.0157   -0.0124
UCL Mean (0.95)    0.0082    0.0163    0.0082    0.0150
Variance           0.0732    0.0836    0.0742    0.0975
Stdev              0.2706    0.2892    0.2724    0.3123
Skewness           0.0106   -0.0004   -0.0014    0.0232
Kurtosis          -1.0040   -1.0083   -1.0043   -0.4159

此表格显示了变量是对称的, 且参数非常接近。

现在, 我们来看看 训练/验证/测试 集合中变量的分布情况:

 boxplot(env$DTn$train %>% 
          dplyr::select(-c(Data, Class)),
        horizontal = T, main = "Train")
abline(v = 0, col = 2)
boxplot(env$DTn$test %>% 
          dplyr::select(-c(Data, Class)),
        horizontal = T, main = "Test")
abline(v = 0, col = 2)
boxplot(env$DTn$val %>% 
          dplyr::select(-c(Data, Class)),
        horizontal = T, main = "Val")
abline(v = 0, col = 2) 

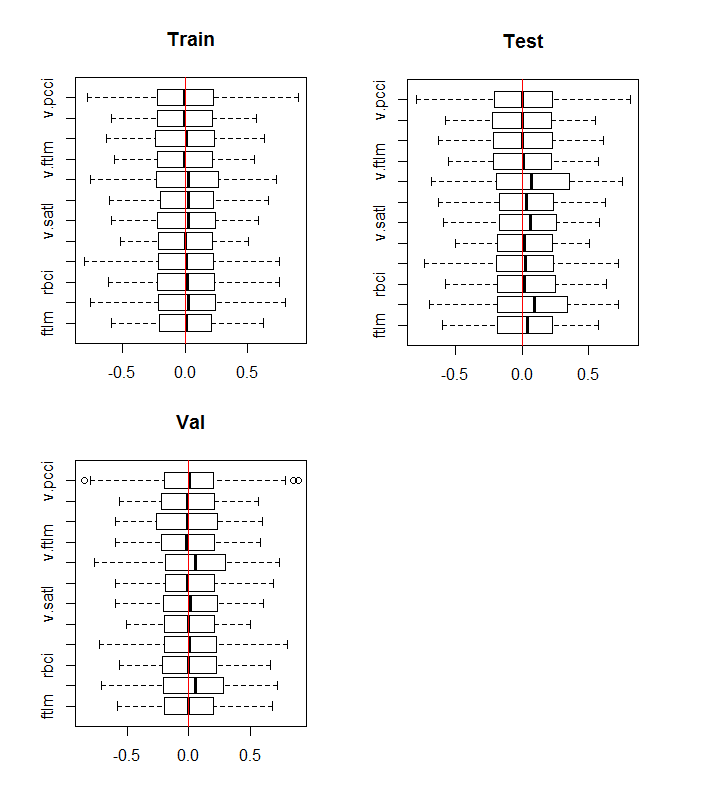
图例.10. 常规化之后训练/验证/测试集合中的变量分布

所有集合的分布几乎相同。我们还要考虑 训练 集合中变量的相关性和协变性

require(GGally)
evalq(ggpairs(DTn$train, columns = 2:7, 
              mapping = aes(color = Class),
              title = "DTn$train1 "), 
      env)
evalq(ggpairs(DTn$train, columns = 8:14, 
              mapping = aes(color = Class),
              title = "DTn$train2"), 
      env)

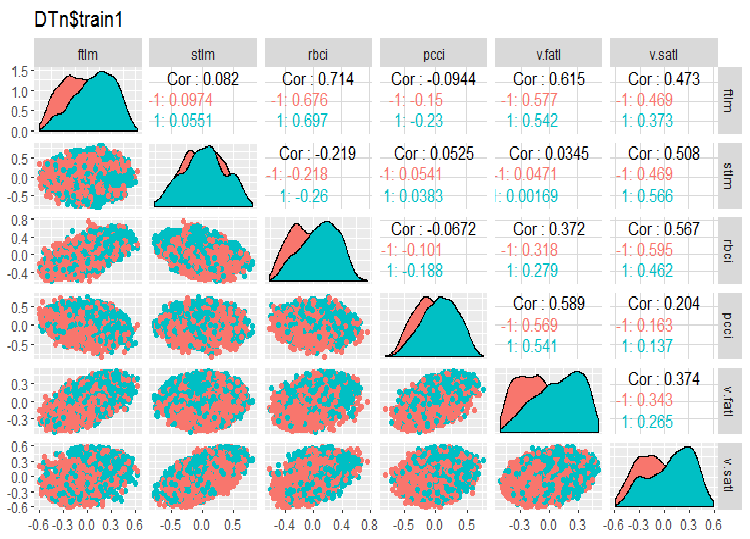
图例.11. 训练集合 1 的变化和协变

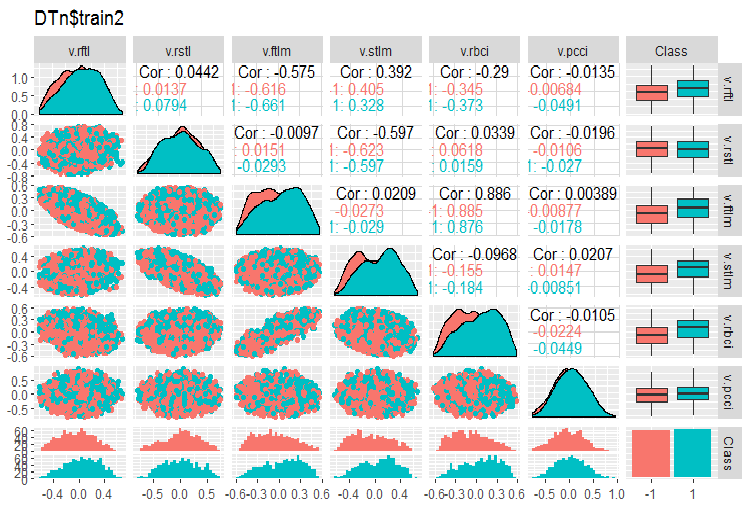
图例.12. 训练集合 2 的变化和协变

没有高度相关的数据, 分布是紧凑的, 没有异常值。数据可以很好地进行切分。表面上, 只有两个有问题的变量 - stlm 和 v.rstl。当我们评估预测因子的相关性时, 我们将会验证这一陈述。现在我们可以看看这些预测因子和目标变量的相关性:

> funModeling::correlation_table(env$DTn$train %>% tbl_df %>%
+                    select(-Data), str_target = 'Class')
   Variable Class
1     Class  1.00
2    v.fatl  0.38
3      ftlm  0.34
4      rbci  0.28
5    v.rbci  0.28
6    v.satl  0.27
7      pcci  0.24
8    v.ftlm  0.22
9    v.stlm  0.22
10   v.rftl  0.18
11   v.pcci  0.08
12     stlm  0.03
13   v.rstl -0.01

已命名变量位于表格的底部, 相关系数非常小。还有, 必须验证 v.pcci. 变量的相关性。我们来检查在 训练/验证/测试 集合中的 v.fatl 变量。

require(ggvis)
evalq(
  DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% 
  group_by(Class) %>%  layer_densities() %>% 
  add_legend("fill", title = "DTn$train$v.fatl"),
  env)
evalq(
  DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% 
    group_by(Class) %>%  layer_densities() %>% 
    add_legend("fill", title = "DTn$val$v.fatl"),
  env)
evalq(
  DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% 
    group_by(Class) %>%  layer_densities() %>% 
    add_legend("fill", title = "DTn$test$v.fatl"),
  env) 

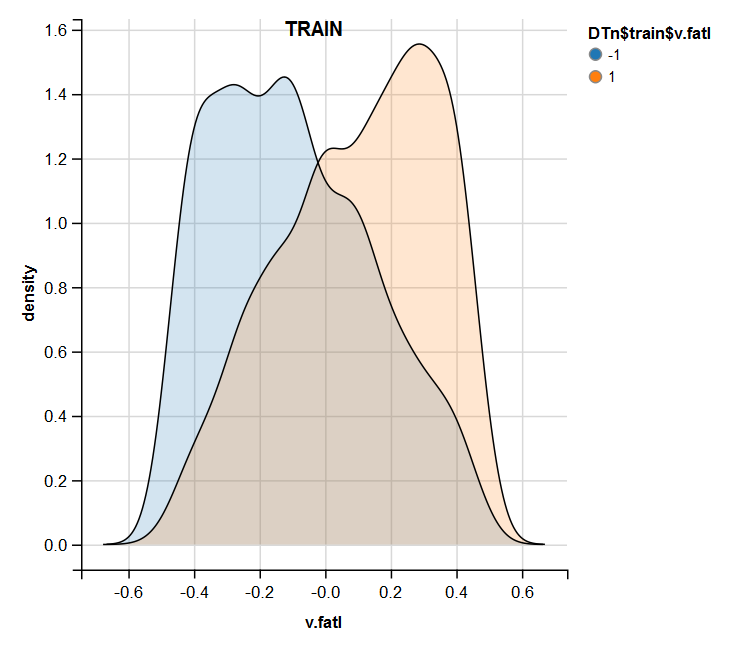
图例.13. 常规化之后训练集合中的 v.fatal 变量分布

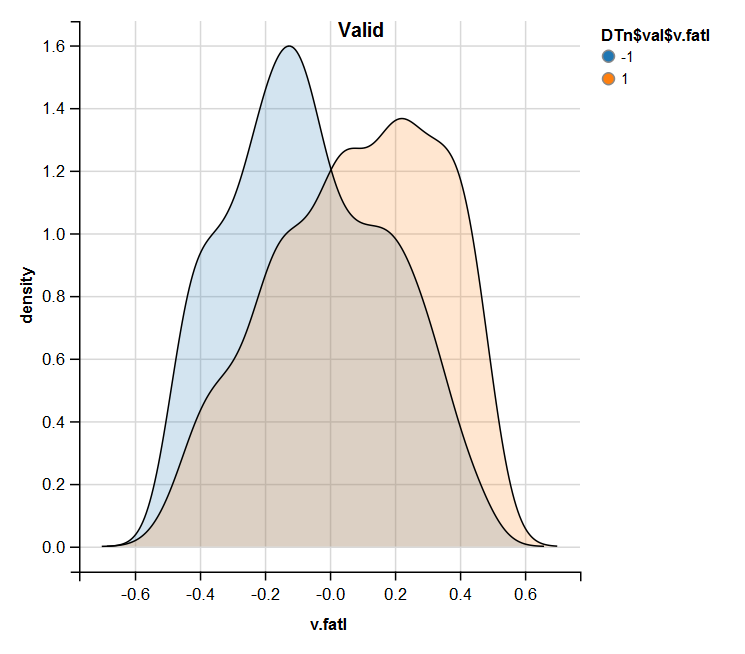
图例.14. 常规化之后验证集合中的 v.fatal 变量分布

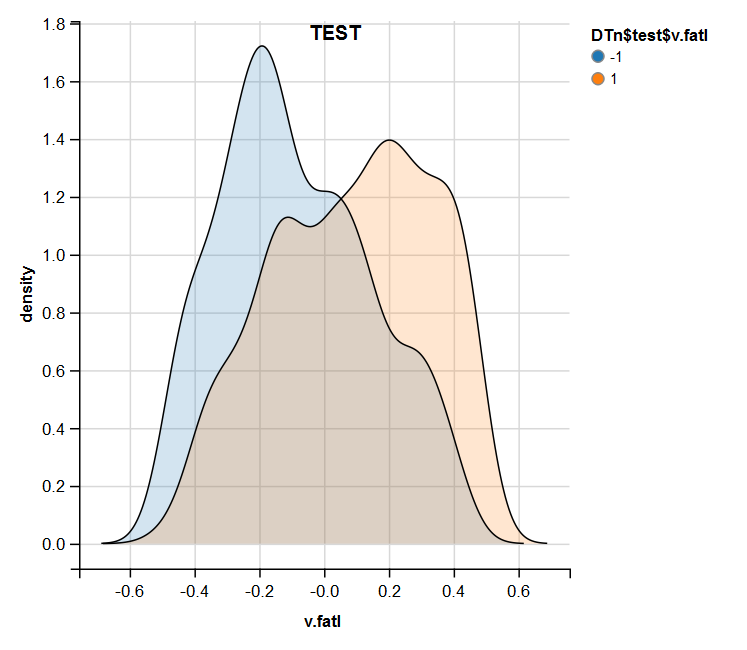
图例.15. 常规化之后测试集合中的 v.fatal 变量分布

进行分析后表明, 常规化通常产生良好的预测因子分布, 没有异常值和高度相关的数据。在很大程度上, 这取决于原始数据的特征。

1.1.3. 离散

离散化 是指将连续变量的值分割为区域从而转换为离散变量的过程。这些区域的边界可以使用各种方法设置。

分离方法可以分为两组: 定量方法, 不涉及与目标变量的关系, 且考虑到目标变量范围的方法。

第一组方法几乎完全被 cut2()::Hmisc 函数所覆盖。样本可以分为指定边界的预定数量区域, 分为四份, 分为每个等同区域上样本数量最少的区域。

第二组方法更有趣, 因为它将变量分割为与目标变量级别相联系的区域。我们来研究几个实现这些方法的软件包。

离散化。这个软件包是一组教练离散算法。这也可以从 "从上到下" 和 "从下到上" 分组, 实现其离散化算法。我们来参考一些我们的 dataSet 例子。

首先, 我们将清除该集合 (不删除高度相关的变量), 然后将其按比例 2000/1000/1000 分割到 训练/验证/测试 集合。

require(discretization)
require(caret)
require(pipeR)
evalq(
  {
    dataSet %>%
    preProcess(.,
               method = c("zv", "nzv", "conditionalX")) %>%
    predict(., dataSet) %>%
    na.omit -> dataSetClean
    train = 1:2000
    val = 2001:3000
    test = 3001:4000
    DT <- list()
    list(train = dataSetClean[train, ], 
         val = dataSetClean[val, ], 
         test = dataSetClean[test, ]) -> DT
  }, 
  env)

我们将使用 mdlp()::discretization 函数, 用最小描述长度描述离散化的。此函数以最小描述长度的熵标准作为停止规则离散矩阵的连续属性。

evalq(
  pipeline({
    DT$train
    select(-Data)
    as.data.frame()
    mdlp()}) -> mdlp.train, envir = env)

函数返回一个含两条插槽的列表。它们是: cutp - 含每个变量截止点的数据帧, 和 Disc.data - 含有标记变量的数据帧。

> env$mdlp.train%>%str()
List of 2
 $ cutp     :List of 12
  ..$ : num [1:2] -0.0534 0.0278
  ..$ : chr "All"
  ..$ : num -0.0166
  ..$ : num [1:2] -0.0205 0.0493
  ..$ : num [1:3] -0.0519 -0.0055 0.019
  ..$ : num 0.000865
  ..$ : num -0.00909
  ..$ : chr "All"
  ..$ : num 0.0176
  ..$ : num [1:2] -0.011 0.0257
  ..$ : num [1:3] -0.03612 0.00385 0.03988
  ..$ : chr "All"
 $ Disc.data:'data.frame':      2000 obs. of  13 variables:
  ..$ ftlm  : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ...
  ..$ stlm  : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ...
  ..$ rbci  : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ...
  ..$ pcci  : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ...
  ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ...
  ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ...
  ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ...
  ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ...
  ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ...
  ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ...
  ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ...
  ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ...
  ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...

第一个插槽告诉我们什么？

我们有三个未标记的变量, 数值与目标变量无关。它们是 2,8 和 12 (stlm, v.rstl, v.pcci)。它们可以被删除, 且不会损失数据集合的品质。请注意, 这些变量在文章的以前部分被定义为无关紧要。

四个变量分为两个类, 三个变量分为三个类, 两个变量分为四个类。

段落 验证/测试 集合, 使用从 训练 集合获得地截止点。为此, 从 训练 中删除未标记的变量, 并将其保存到 train.d 数据帧中。然后, 使用 findInterval() 函数和早前获得的截止点来标记测试/验证 集合。

evalq(
  {
    mdlp.train$cutp %>% 
    lapply(., function(x) is.numeric(x)) %>%
    unlist -> idx   # bool
    #----训练-----------------
    mdlp.train$Disc.data[ ,idx] -> train.d
    #---测试------------
    DT$test %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> test.d
  
    foreach(i = 1:length(idx), .combine = 'cbind') %do% {
      if (idx[i]) {findInterval(test.d[ ,i], 
                   vec = mdlp.train$cutp[[i]],
                   rightmost.closed = FALSE, 
                   all.inside = F,
                   left.open = F)}
    } %>% as.data.frame() %>% add(1) %>%
      cbind(., DT$test$Class) -> test.d
    colnames(test.d) <- colnames(train.d)
    #-----验证-----------------
    DT$val %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> val.d
    foreach(i = 1:length(idx), .combine = 'cbind') %do% {
      if (idx[i]) {findInterval(val.d[ ,i], 
                                vec = mdlp.train$cutp[[i]],
                                rightmost.closed = FALSE, 
                                all.inside = F,
                                left.open = F)}
    } %>% as.data.frame() %>% add(1) %>%
      cbind(., DT$val$Class) -> val.d
    colnames(val.d) <- colnames(train.d)
  },env
)

这些集合是什么样子的？

> env$train.d %>% head()
  ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class
1    3    2    2      4      1      1      2      1      4     1
2    3    2    2      4      1      2      2      1      4     1
3    3    2    1      3      1      2      1      1      3     1
4    3    2    2      4      2      2      1      2      3     1
5    3    2    2      3      2      2      1      2      2     1
6    2    2    1      1      1      2      1      1      1    -1
> env$test.d %>% head()
  ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class
1    1    1    1      2      1      1      1      1      2    -1
2    1    1    3      3      1      1      2      2      3    -1
3    1    1    2      2      1      1      1      2      2    -1
4    2    1    2      3      1      1      2      2      3     1
5    2    2    2      3      1      1      1      2      3     1
6    2    2    2      4      1      1      2      2      3     1
> env$val.d %>% head()
  ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class
1    2    2    2      2      2      2      1      2      2     1
2    2    2    2      2      2      2      1      2      2     1
3    2    2    2      3      2      2      1      2      2     1
4    2    2    2      4      2      2      2      2      3     1
5    2    2    2      3      2      2      1      2      2     1
6    2    2    2      3      2      2      2      2      2     1

> env$train.d$v.fatl %>% table()
.
  1   2   3   4 
211 693 519 577 
> env$test.d$v.fatl %>% table()
.
  1   2   3   4 
 49 376 313 262 
> env$val.d$v.fatl %>% table()
.
  1   2   3   4 
 68 379 295 258 

进一步依据所用的模型使用这些含离散数据的集合。如果这是一个神经网络, 那么预测变量就必须被变换为dummy - 变量。这些变量分为这些类有多好？它们与目标变量的关联度如何？我们用 cross-plot()::funModeling 将这些关系可视化。Cross_plot 显示输入变量如何与接收每个输入的每个范围的相似系数的目标变量相关联。

我们分别将三个变量 v.fatl, ftlm 和 v.satl 分割为 4, 3 和 2 个范围。绘制图表:

evalq(
  cross_plot(data = train.d, 
             str_input = c("v.fatl", "ftlm", "v.satl"), 
             str_target = "Class", 
             auto_binning = F,
             plot_type = "both"), #'quantity' 'percentual'
  env
  )

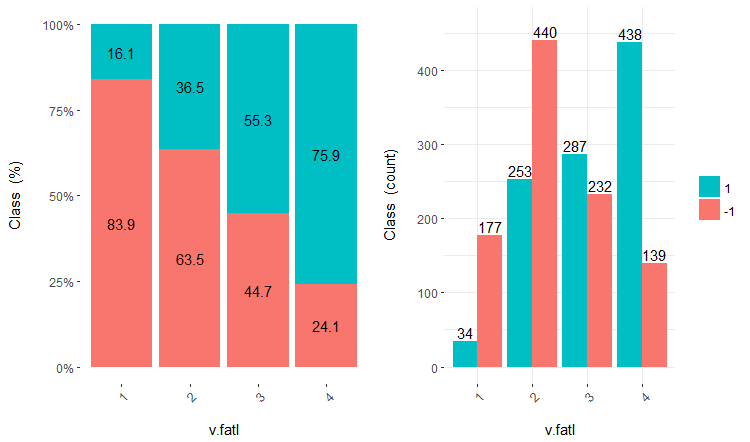
图例.16. v.fatl/类变量的交会图

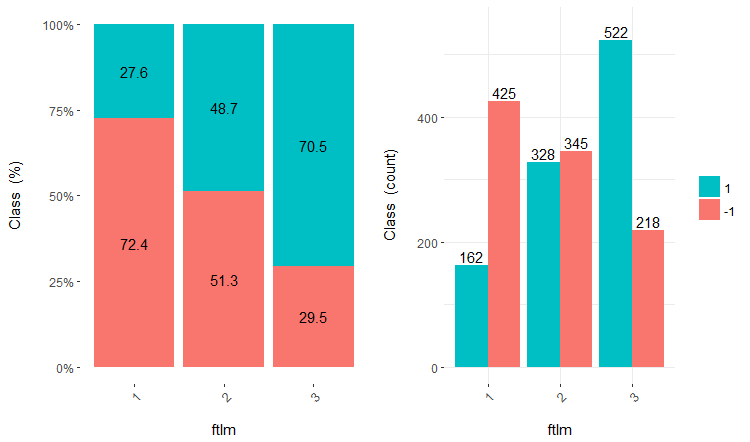
图例.17. ftlm/类变量的交会图

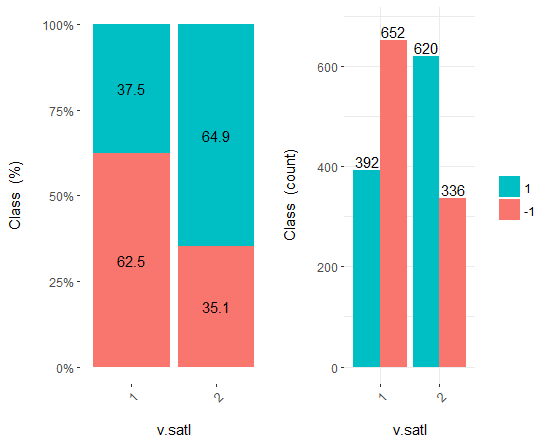
图例.18. v.satl/类变量的交会图

您可看到, 预测变量与目标变量的等级有极佳的相关性, 具有极佳的阈值分割类变量等级。

预测因子可以被简单地划分为相等的区域 (以非优化方式), 以便在这种情况下将它们与目标变量相关联。我们从 训练 集合分隔三个以前的变量和两个坏的变量 (stlm, v.rstl) 为 10 个等同区域, 并看看它们与目标变量的交会图。

evalq(
  cross_plot(
      DT$train  %>% select(-Data) %>%
      select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
      as.data.frame(), 
      str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl), 
      str_target = "Class", 
      auto_binning = T,
      plot_type = "both"), #'quantity' 'percentual'
  env
)

绘制这些变量的五个图表:

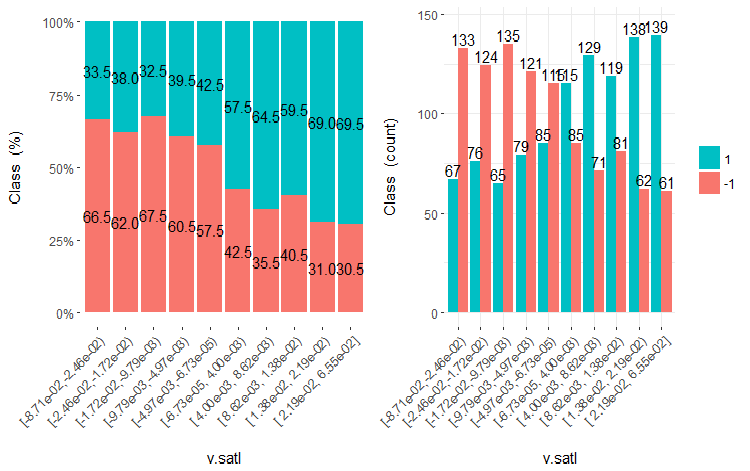
图例.19. v.satl 变量 (10 个区域) 与类的交会图

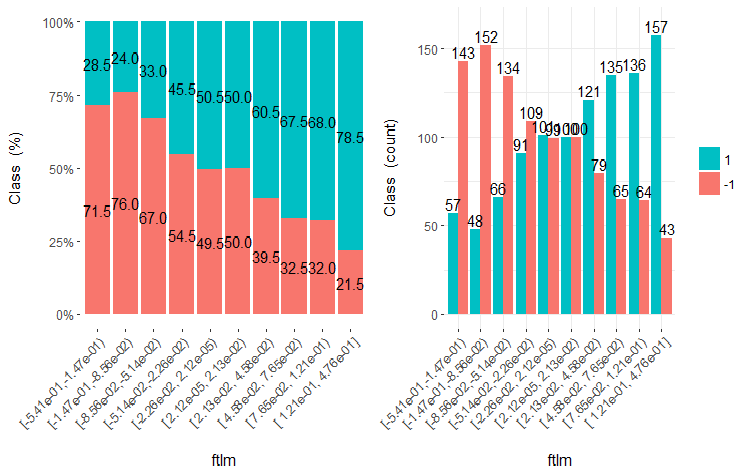
图例.20. ftlml 变量 (10 个区域) 与类的交会图

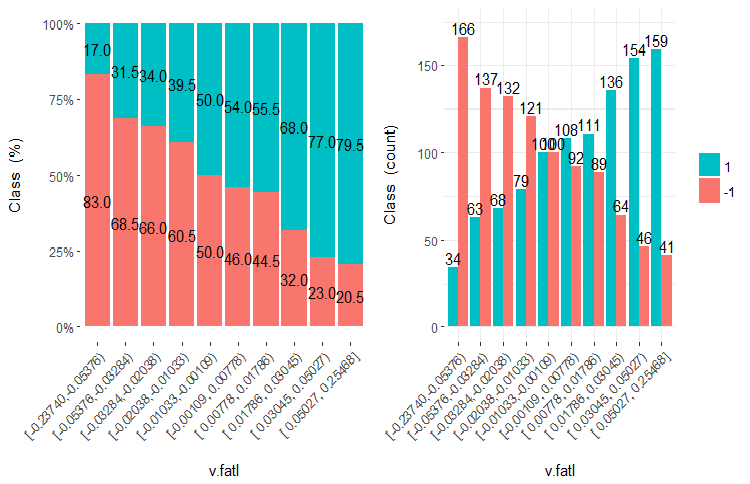
图例.21. v.fatl 变量 (10 个区域) 与类的交会图

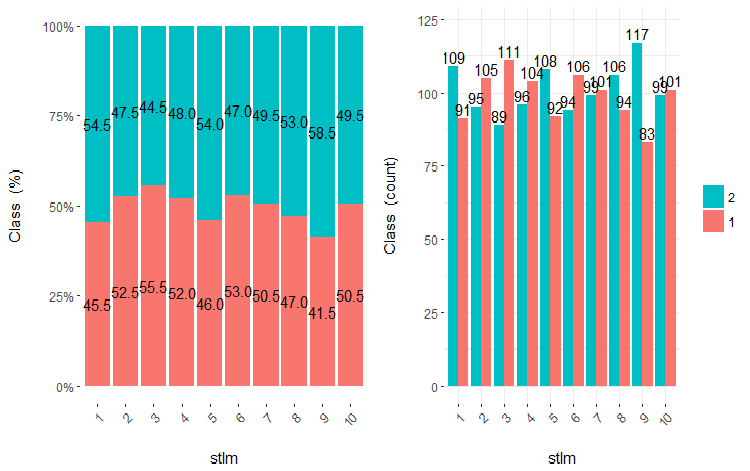
图例.22. stlm 变量 (10 个区域) 与类的交会图

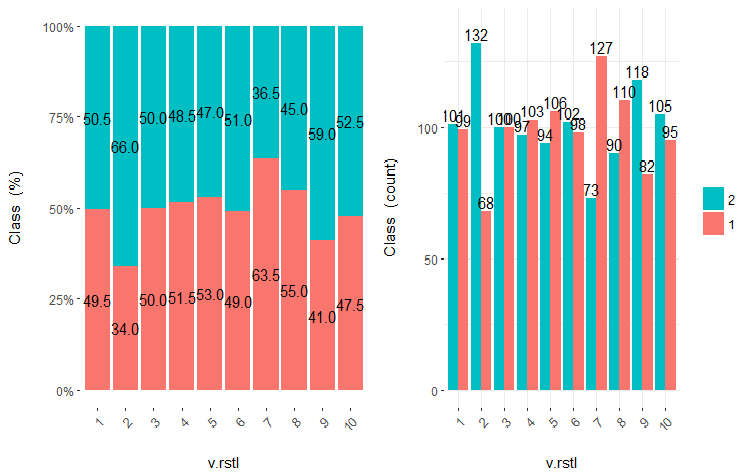
图例.23. v.rstl 变量 (10 个区域) 与类的交会图

从插图中可以清晰明了, 即使变量被划分成 10 个离散的等同效区域, v.fatl, ftlm 和 v.satl 变量具有极佳的变量分割级别阈值。很明显, 为什么两个其它变量 (stlm, v.rstl) 是无关紧要的。这是识别预测因子重要性的有效方式。我们稍后会在这篇文章中回来。

现在, 让我们使用贝叶斯方法 后转换率 进行比较, 看看输入变量如何与目标变量相关联。比较没有内部顺序的分类值很有用。为此, 我们将使用 bayes_plot::funModeling 函数。我们从 train.d, val.d 和 test.d 集合里取 v.fatl, ftlm 和v.satl 变量。

#------BayesTrain-------------------
evalq(
  {
    bayesian_plot(train.d, input = "v.fatl", 
                  target = "Class", 
                  title = "Bayesian comparison train$v.fatl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(train.d, input = "ftlm", 
                  target = "Class", 
                  title = "Bayesian comparison train$ftlm/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(train.d, input = "v.satl", 
                  target = "Class", 
                  title = "Bayesian comparison train$v.satl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
#------------BayesTest------------------------
evalq(
  {
    bayesian_plot(test.d, input = "v.fatl", 
                  target = "Class", 
                  title = "Bayesian comparison test$v.fatl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(test.d, input = "ftlm", 
                  target = "Class", 
                  title = "Bayesian comparison test$ftlm/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(test.d, input = "v.satl", 
                  target = "Class", 
                  title = "Bayesian comparison test$v.satl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
#-------------BayesVal---------------------------------
evalq(
  {
    bayesian_plot(val.d, input = "v.fatl", 
                  target = "Class", 
                  title = "Bayesian comparison val$v.fatl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(val.d, input = "ftlm", 
                  target = "Class", 
                  title = "Bayesian comparison val$ftlm/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
evalq(
  {
    bayesian_plot(val.d, input = "v.satl", 
                  target = "Class", 
                  title = "Bayesian comparison val$v.satl/Class",
                  plot_all = F, extra_above = 5, 
                  extra_under = 5)
  },env
)
#------------------------------------------

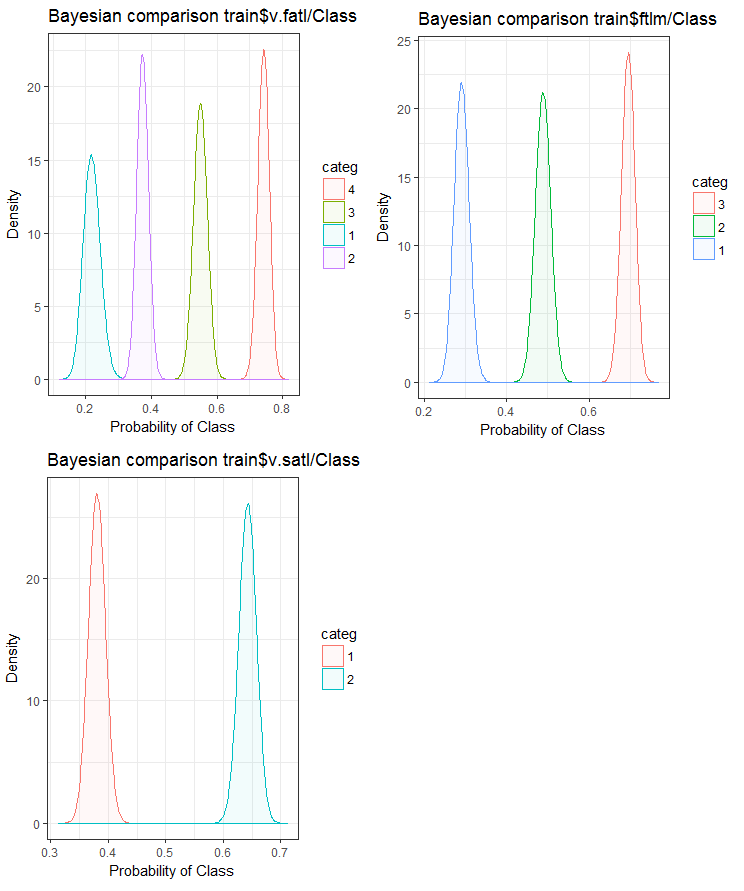
图例.24. 变量与训练集合中的目标变量的贝叶斯比较

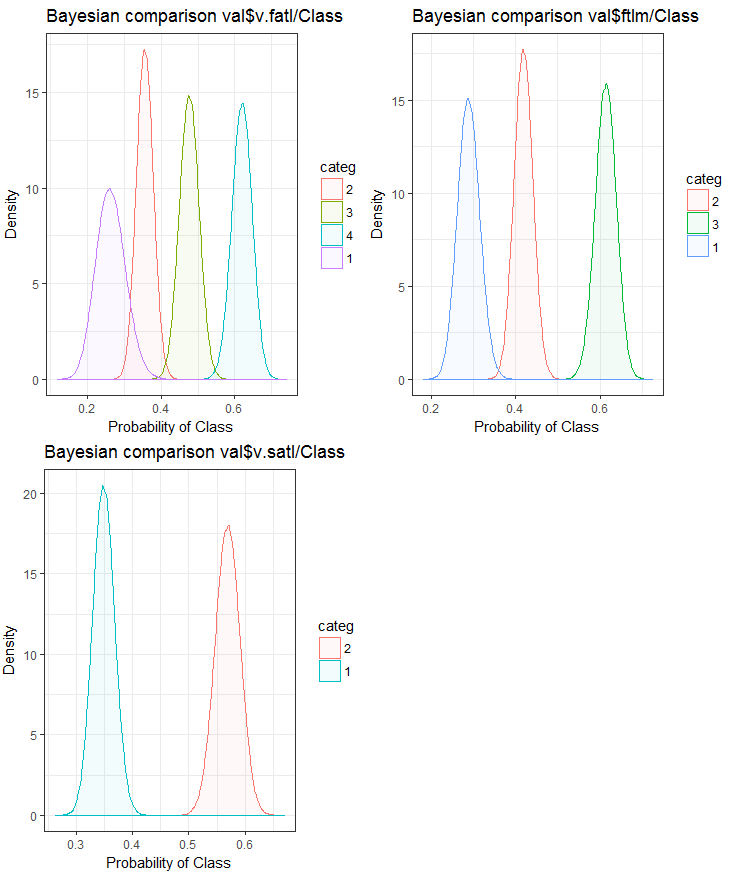
图例.25. 变量与验证集合中的目标变量的贝叶斯比较

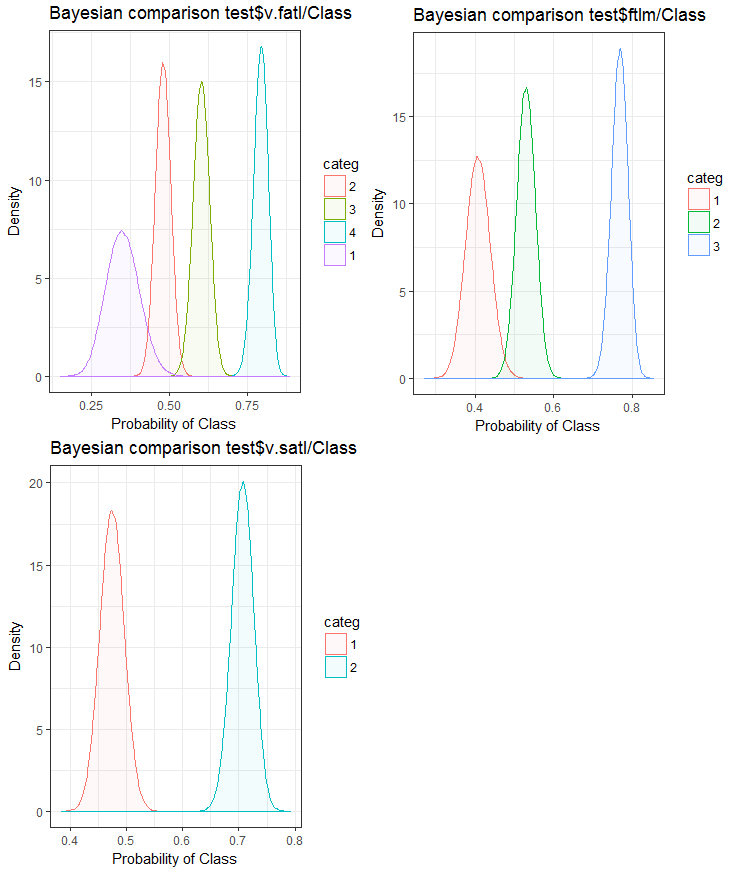
图例.26. 变量与测试集合中的目标变量的贝叶斯比较

我们可以看到, 预测因子与目标变量的相关性在变量中更多地在 4 个等级上漂移。变量中两组的漂移较小。展望未来, 检查仅使用双范围预测因子是如何影响模型准确性是很有用的。

将变量切分为与目标变量等级接近的相适区域的同样任务, 可用另一种方式解决 - 通过使用 smbinning 软件包。您可自行检查一下。之前的 文章 研究过另一种有趣的离散方法。它可以使用 "RoughSets" 软件包来实现。

离散化是变换预测因子的有效方法。不幸的是, 并非所有的模型都可以使用预测因子。

1.2. 创建新特征

创建变量 是根据现有变量创建新变量的过程。让我们看看数据集合, 其中日期 (dd-mm-yy) 是一个输入变量。我们可以创建新的变量, 这将与目标变量 - 日, 月, 年, 星期几更好地联系起来。此步骤用于显示变量中的隐藏关系。

创建派生变量 是指使用一组函数和现有变量中的各种方法创建新变量的过程。要创建的变量类型取决于商业分析师的好奇心, 假设集合及他们的理论知识。方法的选择是广泛的。取对数, 分割, 提高到 n 次幂只是变换方法的少数示例。 

创建虚拟变量 是处理变量的另一种流行方法。通常使用虚拟变量将分类变量转换为数值变量。分类变量的可取值为 0 和 1。我们可以为 两个类别变量以上的类, 譬如 N 和 N-1 个变量, 创建虚拟变量。

在本文中, 我们作为分析师以日线级为基础讨论遇到的情况。下面列出从数据集合中提取最大信息的若干方法。

1. 使用数据和时间的数值作为变量。可以考虑通过日期和时间的差异来创建新变量。
2. 创建新的比率和比例。不光将过去的输入和输出存储在数据集合中, 它们的比率也可包括在内。这可能有更大的意义。
3. 使用标准变换。观察一下变量的波动以及变量一并输出的面积, 我们可以看出在基本变换后相关性是否会有所改善。最常用的变换是对数, 指数, 平方和三角函数变体。
4. 检查变量的季节性, 并创建所需区间 (周, 月, 时段, 等等) 的模型。

直观的是, 星期一的市场行为与星期三和星期四不同。这意味着星期几是一个重要的特征。日内的时间对于市场同样重要。它定义了是否为亚洲, 欧洲还是美国时段。我们如何定义这些特征？

我们将使用 timekit 软件包。tk_augment_timeseries_signature() 是软件包的中心特征。这将初始数据集合 pr 的时间标签添加到整个时间数据行中, 可用作附加特征和组参数。它们是什么样的数据？

Index	已解决的索引值
Index.num	以秒为单位的索引值。基数 "1970-01-01 00:00:00"
diff	与之前索引值的差值, 以秒为单位
Year	年份, 索引组成部分
half	半年, 索引组成部分
quarter	季度, 索引组成部分
month	月份, 索引组成部分
month.xts	月份, 以 0 为基数, 索引组成部分, 与 xts 中的实现相同
month.lbl	月份标签作为排序因子。始自一月份, 终于十二月份
day	日期, 索引组成部分
hour	小时, 索引组成部分
minute	分钟, 索引组成部分
second	秒, 索引组成部分
hour12	以 12-小时为基础的小时部分
am.pm	早上 (am) = 1, 午后 (pm) = 2
wday	基数为 1 的周内天数, 周日 = 1, 周六 = 7
wday.xts	周内天数, 以 0 为基数, 与 xts 中的实现相同周日 = 0, 周六 = 6
wday.lbl	周内天数的标签作为排序因子。始自周日, 终于周六
mday	月内天数
qday	季度内天数
yday	年内天数
mweek	月内周数
week	年内周数 (始自周日)
week.iso	依据 ISO 的年内周数 (始自周一)
week2	两周的模块
week3	三周的模块
week4	四周的模块

我们取初始数据集合 pr, 用 tk_augment_timeseries_signature() 函数加强它, 将 mday, wday.lbl, hour, 变量添加到初始数据集合中, 删除依据周内天数的未定义变量 (NA) 和组数据。

evalq(
  {
    tk_augment_timeseries_signature(pr) %>%
    select(c(mday, wday.lbl,  hour)) %>% 
    cbind(pr, .) -> pr.augm
    pr.compl <- pr.augm[complete.cases(pr.augm), ]
    pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest() 
  },
  env)
> str(env$pr.augm)
'data.frame':   8000 obs. of  33 variables:
 $ Data    : POSIXct, format: "2017-01-10 11:00:00" ...
 $ Open    : num  123 123 123 123 123 ...
 $ High    : num  123 123 123 123 123 ...
 $ Low     : num  123 123 123 123 123 ...
 $ Close   : num  123 123 123 123 123 ...
 $ Vol     : num  3830 3360 3220 3241 3071 ...
 ..................................................
 $ zigz    : num  123 123 123 123 123 ...
 $ dz      : num  NA -0.0162 -0.0162 -0.0162 -0.0162 ...
 $ sig     : num  NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
 $ mday    : int  10 10 10 10 10 10 10 10 10 10 ...
 $ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
 $ hour    : int  11 11 11 11 12 12 12 12 13 13 ...

如果我们使用 lubridate 函数库可以得到相同的结果, 删除了星期六的数据。

require(lubridate)
evalq({pr %>% mutate(.,
                     wday = wday(Data), #label = TRUE, abbr = TRUE),
                     day = day(Data),
                     hour = hour(Data)) %>%
    filter(wday != "Sat") -> pr1
  pr1.nest <- pr1 %>% na.omit %>% 
    group_by(wday) %>% nest()}, 
  env
)
#-------
str(env$pr1)
'data.frame':   7924 obs. of  33 variables:
 $ Data  : POSIXct, format: "2017-01-10 11:00:00" ...
 $ Open  : num  123 123 123 123 123 ...
 $ High  : num  123 123 123 123 123 ...
 $ Low   : num  123 123 123 123 123 ...
 $ Close : num  123 123 123 123 123 ...
 $ Vol   : num  3830 3360 3220 3241 3071 ...
 ..........................................
 $ zigz  : num  123 123 123 123 123 ...
 $ dz    : num  NA -0.0162 -0.0162 -0.0162 -0.0162 ...
 $ sig   : num  NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
 $ wday  : int  3 3 3 3 3 3 3 3 3 3 ...
 $ day   : int  10 10 10 10 10 10 10 10 10 10 ...
 $ hour  : int  11 11 11 11 12 12 12 12 13 13 ...

数据按周内天数分组如下所示 (星期日 = 1, 星期一 = 2 以此类推):

> env$pr1.nest
# A tibble: 5 × 2
   wday                  data
  <int>                <list>
1     4 <tibble [1,593 Ч 32]>
2     5 <tibble [1,632 Ч 32]>
3     6 <tibble [1,624 Ч 32]>
4     2 <tibble [1,448 Ч 32]>
5     3 <tibble [1,536 Ч 32]>

另外, 来自 pr 数据集合的 dL, dH 变量可以在最后三根柱线上使用。

2. 选择预测因子

评估预测因子的重要性有很多方法和标准。其中一些已在之前的文章中研究过。因此在本文中, 重点是可视化, 我们会比较一个可视方案和一个分析方法, 来提高预测因子的重要性。

2.1. 直观评估

我们将使用 smbinning 软件包。早前, 我们使用了 funModeling 来评估预测变量。我们得出的结论, 可视化的关系是一种简单而可靠的方法来确定预测因子的相关性。我们将继续测试 smbinning 软件包是如何处理数据常规化和变换的。我们还将了解预测变量如何影响其重要性。

收集一套对数变换, 正弦变换, 三角变换和常规化数据, 并评估目标变量和预测变量在这些集合中的依赖关系。

主要集合的处理顺序 (如下图所示) 如下: 清理 dataSet 中的原始数据 (不要删除高度相关的数据), 将 dataSet 分割到 训练/验证/测试 集合并获取 DT 集合。然后根据下面的示意针对每种变换类型执行动作。我们在一个脚本中收集一切:

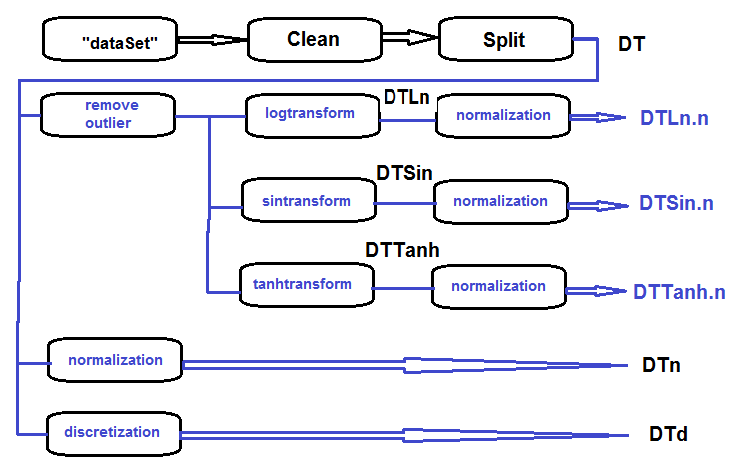
图例.27. 初步处理框图

清理集合, 将其分隔成 训练/验证/测试 集合并删除不必要的数据:

#----清理---------------------
require(caret)
require(pipeR)
evalq(
  {
    train = 1:2000
    val = 2001:3000
    test = 3001:4000
    DT <- list()
    dataSet %>%
      preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
      predict(., dataSet) %>%
      na.omit -> dataSetClean
    list(train = dataSetClean[train, ], 
         val = dataSetClean[val, ], 
         test = dataSetClean[test, ]) -> DT
    rm(dataSetClean, train, val, test)
  }, 
  env)

在所有集合里处理异常值:

#------异常值-------------
evalq({
# 定义结果的新列表
  DTcap <- list()
# 遍历三个套合
  foreach(i = 1:3) %do% {
    DT[[i]] %>% 
# 删除 (数据, 类) 列
      select(-c(Data, Class)) %>%
# 转换成 data.frame 并存储在临时变量 x 中
      as.data.frame() -> x
    if (i == 1) {
# 定义第一个输入中异常值的参数
      foreach(i = 1:ncol(x), .combine = "cbind") %do% {
        prep.outlier(x[ ,i]) %>% unlist()
      } -> pre.outl
      colnames(pre.outl) <- colnames(x)
    } 
# 将异常值替换为 5/95％, 并将结果存储在 x.cap 中
    foreach(i = 1:ncol(x), .combine = "cbind") %do% {
      stopifnot(exists("pre.outl", envir = env))
      lower = pre.outl['lower.25%', i] 
      upper = pre.outl['upper.75%', i]
      med = pre.outl['med', i]
      cap1 = pre.outl['cap1.5%', i] 
      cap2 = pre.outl['cap2.95%', i] 
      treatOutlier(x = x[ ,i], impute = T, fill = T, 
                   lower = lower, upper = upper, 
                   med = med, cap1 = cap1, cap2 = cap2) 
      } %>% as.data.frame() -> x.cap
    colnames(x.cap) <- colnames(x)
    return(x.cap)
  } -> Dtcap
# 删除不必要的变量
  rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)

在所有 Dtcap 集合中变换变量, 不含 log(x+1) 函数的异常值。得到的 DTLn 列表含对数变换变量的三个集合

#------对数变换------------
evalq({
  DTLn <- list()
  foreach(i = 1:3) %do% {
    DTcap[[i]] %>% 
      apply(., 2, function(x) log2(x + 1)) %>%
      as.data.frame() %>%
      cbind(., Class = DT[[i]]$Class)
  } -> DTLn
},
env)

在所有 Dtcap 集合中变换变量, 不含 sin(2*pi*x) 函数的异常值。得到的 DTSin 列表含正弦变换变量的三个集合

#------正弦变换--------------
evalq({
  DTSin <- list()
  foreach(i = 1:3) %do% {
    DTcap[[i]] %>% 
      apply(., 2, function(x) sin(2*pi*x)) %>%
      as.data.frame() %>%
      cbind(., Class = DT[[i]]$Class)
  } -> DTSin
},
env)

在所有 Dtcap 集合中变换变量, 不含 tanh(x) 函数的异常值。得到的 DTTanh 列表含三角变换变量的三个集合

#------三角变化----------
evalq({
  DTTanh <- list()
  foreach(i = 1:3) %do% {
    DTcap[[i]] %>% 
      apply(., 2, function(x) tanh(x)) %>%
      as.data.frame() %>%
      cbind(., Class = DT[[i]]$Class)
  } -> DTTanh
},
env)

常规化 DT, DTLn, DTSin, DTTanh 集合。

#------常规化-----------
evalq(
  {
# 定义常规化参数
    preProcess(DT$train, method = "spatialSign") -> preproc 
    list(train = predict(preproc, DT$train), 
         val = predict(preproc, DT$val),
         test = predict(preproc, DT$test)
 ) -> DTn
  }, 
  env) 
#--对数---
evalq(
  {
    preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn 
    list(train = predict(preprocLn, DTLn[[1]]), 
         val = predict(preprocLn, DTLn[[2]]),
         test = predict(preprocLn, DTLn[[3]])
    ) -> DTLn.n
  }, 
  env)
#---正弦---
evalq(
  {
    preProcess(DTSin[[1]], method = "spatialSign") ->  preprocSin 
    list(train = predict(preprocSin, DTSin[[1]]), 
         val = predict(preprocSin, DTSin[[2]]),
         test = predict(preprocSin, DTSin[[3]])
    ) -> DTSin.n
  }, 
  env)
#-----三角变换-----------------
evalq(
  {
    preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh 
    list(train = predict(preprocTanh, DTTanh[[1]]), 
         val = predict(preprocTanh, DTTanh[[2]]),
         test = predict(preprocTanh, DTTanh[[3]])
    ) -> DTTanh.n
  }, 
  env)

使用 mdlp::discretization 函数来离散 DT 集合

##------离散----------
#--------preCut---------------------
# 定义切点
require(pipeR)
require(discretization)
evalq(
  #require(pipeR) 
# 需要一点时间！
  pipeline({
    DT$train
    select(-Data)
    as.data.frame()
    mdlp() 
  }) -> mdlp.train, 
  env)
#-------cut_opt----------
evalq(
  {
    DTd <- list()
    mdlp.train$cutp %>% 
# 定义必须离散的列
      lapply(., function(x) is.numeric(x)) %>%
      unlist -> idx   # bool
    #----训练-----------------
    mdlp.train$Disc.data[ ,idx] -> DTd$train 
    #---测试------------
    DT$test %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> test.d
# 根据计算的范围重新分配数据    
    foreach(i = 1:length(idx), .combine = 'cbind') %do% {
      if (idx[i]) {
        findInterval(test.d[ ,i], 
        vec = mdlp.train$cutp[[i]],
        rightmost.closed = FALSE, 
        all.inside = F,
        left.open = F)
        }
    } %>% as.data.frame() %>% add(1) %>%
      cbind(., DT$test$Class) -> DTd$test
    colnames(DTd$test) <- colnames(DTd$train)
    #-----验证-----------------
    DT$val %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> val.d
# 根据计算的范围重新分配数据  
    foreach(i = 1:length(idx), .combine = 'cbind') %do% {
      if (idx[i]) {
        findInterval(val.d[ ,i], 
        vec = mdlp.train$cutp[[i]],
        rightmost.closed = FALSE, 
        all.inside = F,
        left.open = F)
        }
    } %>% as.data.frame() %>% add(1) %>%
      cbind(., DT$val$Class) -> DTd$val 
    colnames(DTd$val) <- colnames(DTd$train)
# 整理
    rm(test.d, val.d)
  }, 
  env
)

我们回想一下 DT$train 原始数据集合中的变量:

require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)

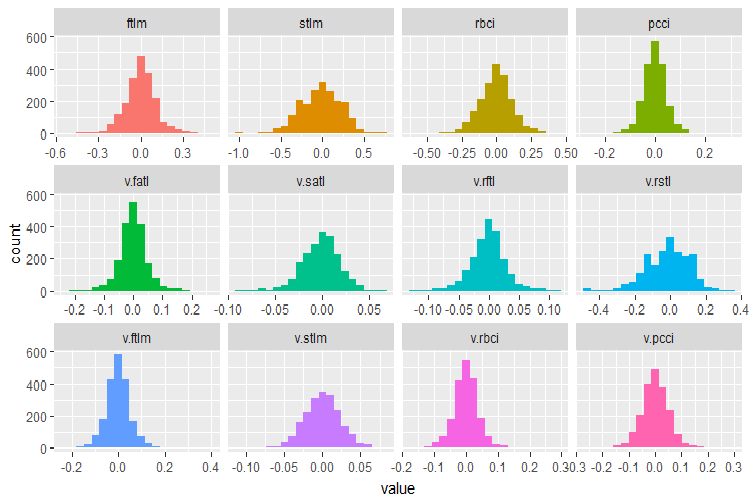
图例.28. 在 DT$train 数据集合中分配变量

利用 smbinning 软件包的能力来识别 训练 子集早前所获 (Dtn, DTLn.n, DTSin.n 和 DTTanh.n) 的所有常规化数据集合之中的相关预测因子。在此软件包中的目标变量必须是数字, 并具有值 (0, 1)。我们来编写一个必要的变换函数。

#--------------------------------
require(smbinning)
targ.int <- function(x){
  x %>% tbl_df() %>%
  mutate(Cl = (as.numeric(Class) - 1) %>%
           as.integer()) %>%
  select(-Class) %>% as.data.frame()
}

此外, 此程序包不接受名称中有点的变量。下面的函数将所有变量名中的点重新命名为具有下划线的变量。

renamepr <- function(X){
  X %<>% rename(v_fatl = v.fatl,
               v_satl = v.satl,
               v_rftl = v.rftl,
               v_rstl = v.rstl,
               v_ftlm = v.ftlm,
               v_stlm = v.stlm,
               v_rbci = v.rbci,
               v_pcci = v.pcci)
  return(X)
}

用相关预测值计算并绘制图表。

par(mfrow = c(2,2))
#--对数--------------
evalq({
  df <- renamepr(DTLn.n[[1]]) %>% targ.int
  sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7)
  rm(df)
}, 
env)
#---正弦-----------------
evalq({
  df <- renamepr(DTSin.n[[1]]) %>% targ.int
  sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7)
  rm(df)
  }, 
env)
#---常规化-------------
evalq({
  df <- renamepr(DTn[[1]]) %>% targ.int
  sumivt.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.n, cex = 0.7)
  rm(df)
  }, 
env)
#-----三角变换----------------
evalq({
  df <- renamepr(DTTanh.n[[1]]) %>% targ.int
  sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7)
  rm(df)
  }, 
env)
par(mfrow = c(1,1))

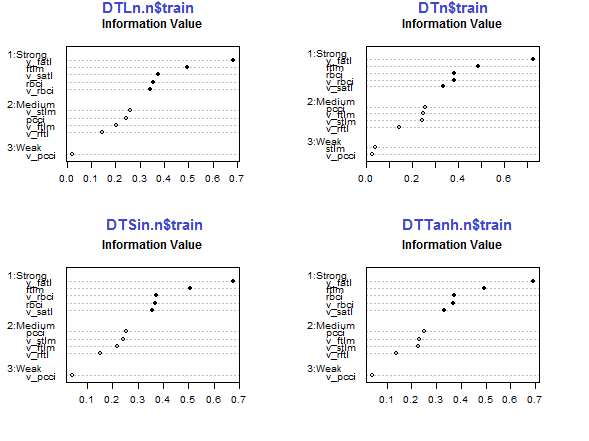
图例.29. 预测因子在常规化集合的训练子集中的重要性

五个预测因子 v_fatl, ftlm, v_satl, rbci, v_rbci 在所有集合中均很强,, 尽管它们的顺序不同。四个预测因子 pcci, v_ftlm, v_stlm, v_rftl 强度平均。预测因子 v_pcci 和 stlm 较弱。变量的分布可以按照每个集合的重要性顺序来查看:

env$sumivt.ln.n
     Char     IV               Process
5  v_fatl 0.6823    Numeric binning OK
1    ftlm 0.4926    Numeric binning OK
6  v_satl 0.3737    Numeric binning OK
3    rbci 0.3551    Numeric binning OK
11 v_rbci 0.3424    Numeric binning OK
10 v_stlm 0.2591    Numeric binning OK
4    pcci 0.2440    Numeric binning OK
9  v_ftlm 0.2023    Numeric binning OK
7  v_rftl 0.1442    Numeric binning OK
12 v_pcci 0.0222    Numeric binning OK
2    stlm     NA No significant splits
8  v_rstl     NA No significant splits

最后三个变量可以被舍弃。这样只保留五个最强和四个平均值。我们定义最佳变量 (IV > 0.1) 的名称。

evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% 
        na.omit %>% as.character() -> best.sin.n, 
      env)
> env$best.sin.n
[1] "v_fatl" "ftlm"   "rbci"   "v_rbci" "v_satl" "pcci"  
[7] "v_ftlm" "v_stlm" "v_rftl"

我们更详细地观察 v_fatlиftlm 变量。

evalq({
    df <- renamepr(DTTanh.n[[1]]) %>% targ.int
    x = 'v_fatl'
    y = 'Cl'
    res <- smbinning(df = df, 
                        y = y,
                        x = x) 
  #res$ivtable # 制表和信息值
  #res$iv # 信息值
  #res$bands # 箱或带
  #res$ctree  # Partykit 决策树
  par(mfrow = c(2,2))
  sub = paste0(x, "  vs  ", y) #rbci vs Cl"
  boxplot(df[[x]]~df[[y]],
          horizontal = TRUE, 
          frame = FALSE, col = "lightblue",
          main = "Distribution")
  mtext(sub,3) #ftlm
  smbinning.plot(res, option = "dist",
                 sub = sub) #"pcci vs Cl")
  smbinning.plot(res, option = "goodrate", #"badrate"
                 sub = sub) #"pcci vs Cl")
  smbinning.plot(res, option = "WoE",
                 sub = sub) #"pcci vs Cl")
  par(mfrow = c(1, 1))
}, env)

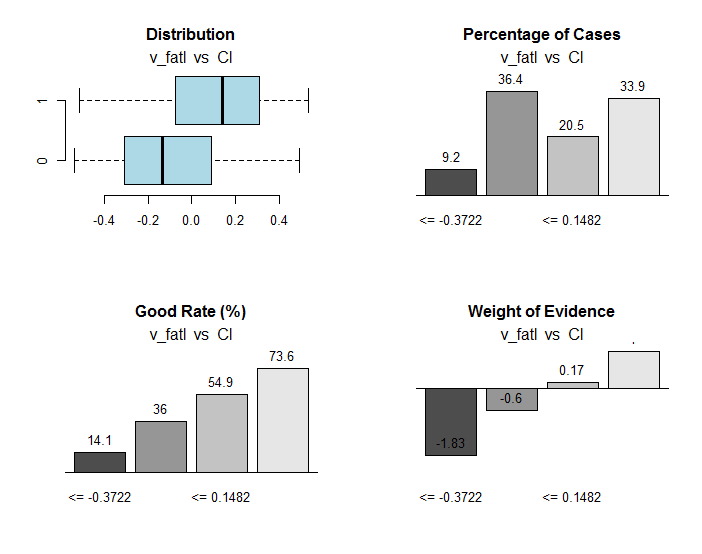
图例.30. 将 v_fatl 变量的范围与 Cl 目标变量相连

除了有用的信息, res 对象包含将变量分割成与目标变量连接的最佳范围的点。在我们这种特殊的情况下, 有四个范围。

> env$res$cuts
[1] -0.3722 -0.0433  0.1482

我们将对 ftlm 变量和图表进行相同的计算:

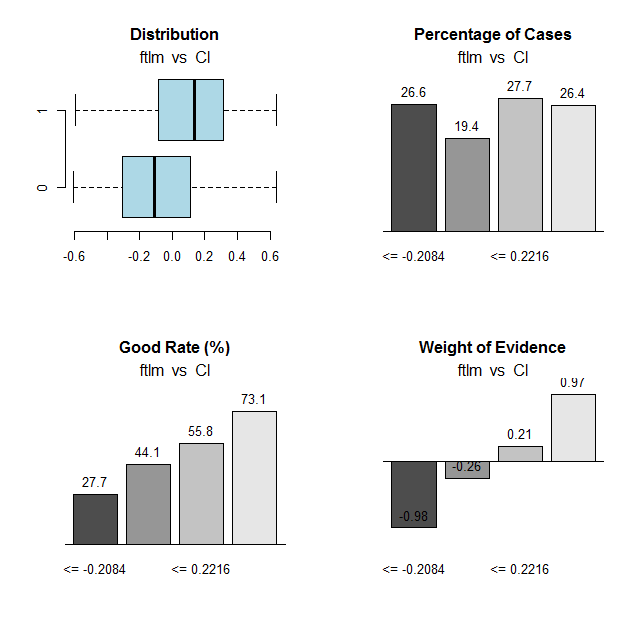
图例.31. 将 ftlm 变量的范围与 Cl 目标变量连接

范围截止点:

> env$res$cuts
[1] -0.2084 -0.0150  0.2216

截止点允许我们将变量离散到集合中, 并查看以下项目有多少差异:

• 早前使用 mdlp::discretization 函数定义的重要变量来自使用 smbinning::smbinning; 函数定义的变量
• 将变量切分到范围。

我们已经有一个利用 mdlp::discretization DTd 函数离散化的数据集合。我们要做同样的事情, 但是这次我们仅针对 训练 子集使用 smbinning::smbinning 函数。

定义切点:

evalq({
  res <- list()
  DT$train %>% renamepr() %>% targ.int() -> df
  x <- colnames(df)
  y <- "Cl"
  foreach(i = 1:(ncol(df) - 1)) %do% {
    smbinning(df, y = y, x = x[i])
  } -> res
  res %>% lapply(., function(x) x[1] %>% is.list) %>%
    unlist -> idx
}, env) 

离散 DT$train: 子集

evalq({
  DT1.d <- list()
  DT$train %>% renamepr() %>% 
    targ.int() %>% select(-Cl) -> train
  foreach(i = 1:length(idx), .combine = 'cbind') %do% {
    if (idx[i]) {
      findInterval(train[ ,i], 
                   vec = res[[i]]$cuts,
                   rightmost.closed = FALSE, 
                   all.inside = F,
                   left.open = F)
    }
  } %>% as.data.frame() %>% add(1) %>%
    cbind(., DT$train$Class) -> DT1.d$train
  colnames(DT1.d$train) <- colnames(train)[idx] %>%
    c(., 'Class')
},
env)

按照重要性大于 0.1 的升序识别最佳变量:

evalq({
  DT$train %>% renamepr() %>% targ.int() -> df
  sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
  sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>% 
    na.omit %>% as.character() -> best.dt1.d
  rm(df)
}, 
env)

在 DTd$train: 集合中绘制分割变量的图表

require(funModeling)
plot_num(env$DTd$train)

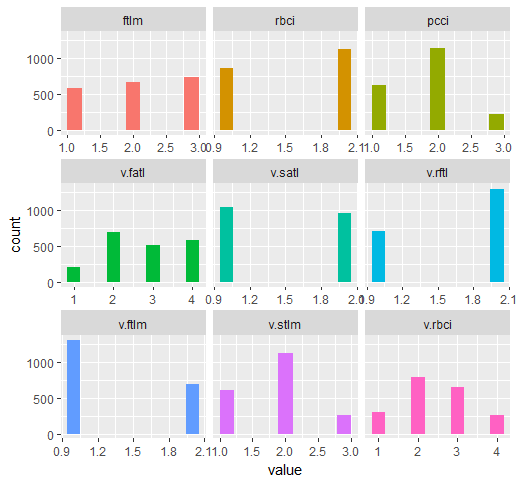
图例.32. 使用 mdlp 函数离散 DT$ train 的变量

含有所有变量和最佳变量的 DT1.d 图表如下所示。

plot_num(env$DT1.d$train)

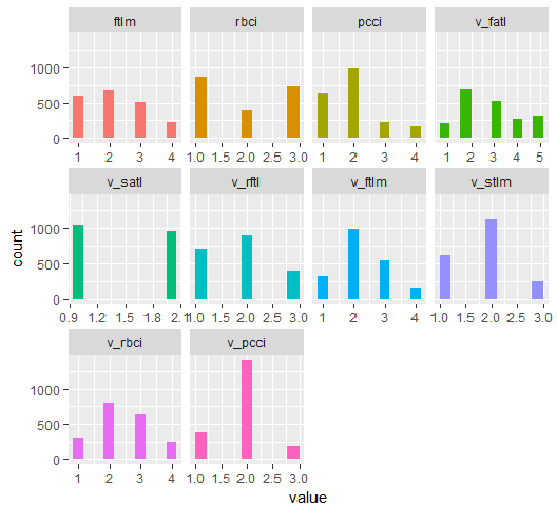
图例.33. 利用 smbinning 函数离散 DT1 d$train 集合的变量

plot_num(env$DT1.d$train[ ,env$best.dt1.d])

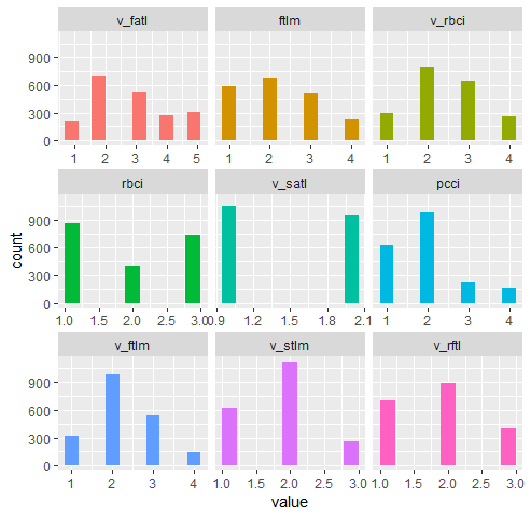
图例.34. 利用 smbinning 函数离散 DT1.d$train 集合变量 (最好按照信息重要性的顺序排列)

我们可以从图表当中看出什么？定义为重要的变量在两种情况下都是相同的, 但是分割的范围是不同的。必须针对模型测试哪个变体给出更好的预测。

2.2. 分析评估

有众多分析方法可通过各种标准来识别预测因子的重要性。我们早前已研究过其中一些。现在, 我想测试一个不同寻常的方法来选择预测因子。

我们将使用 varbvs 软件包。在 varbvs 中已实现的函数有: 安装选择变量的贝叶斯模型的快速算法, 计算贝叶斯系数, 其结果 (或目标变量) 是线性回归, 或逻辑回归。这些算法基于 "回归中贝叶斯变量选择的可缩放变分推理及其在遗传关联研究中的准确性" 中描述的变分近似。 (P. Carbonetto 和 M. Stephens, 贝叶斯分析 7 月, 2012, 页 73-108)。该软件用于处理含有超过一百万个变量和数千个样本的大型数据集合。

varbvs() 函数接收矩阵, 目标变量接收数字向量 (0,1) 作为输入数据。使用这种方法, 我们来测试哪些预测因子将在我们的常规化数据集合 DTTanh.n$train 中担当重任。

require(varbvs)
evalq({
  train <- DTTanh.n$train %>% targ.int() %>%  as.matrix()
  fit <- varbvs(X = train[ ,-ncol(train)] , 
                Z = NULL,
                y = train[ ,ncol(train)] %>% as.vector(),
                "binomial", 
                logodds = seq(-2,-0.5,0.1),
                optimize.eta = T,
                initialize.params = T,
                verbose = T, nr = 100
                )
  print(summary(fit))
}, env)

Welcome to           --       *                              *               
VARBVS version 2.0.3 --       |              |               |               
large-scale Bayesian --       ||           | |    |          || |     |   |  
variable selection   -- |     || | |    |  | ||  ||        |||| ||    |   || 
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family:     binomial   num. hyperparameter settings: 16 
samples:    2000       convergence tolerance         1.0e-04
variables:  12         iid variable selection prior: yes 
covariates: 0          fit prior var. of coefs (sa): yes 
intercept:  yes        fit approx. factors (eta):    yes 
Finding best initialization for 16 combinations of hyperparameters.
-iteration-   variational    max.   incl variance params
outer inner   lower bound  change   vars   sigma      sa
 0016 00018 -1.204193e+03 6.1e-05 0003.3      NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration-   variational    max.   incl variance params
outer inner   lower bound  change   vars   sigma      sa
 0016 00002 -1.204193e+03 3.2e-05 0003.3      NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family:     binomial   num. hyperparameter settings: 16
samples:    2000       iid variable selection prior: yes
variables:  12         fit prior var. of coefs (sa): yes
covariates: 1          fit approx. factors (eta):    yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters: 
        estimate Pr>0.95             candidate values
sa          3.49 [3.25,3.6]          NA--NA
logodds    -0.75 [-1.30,-0.50]       (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95 
    3     3     3     3     3     3 
Top 5 variables by inclusion probability:
  index variable   prob PVE coef*  Pr(coef.>0.95)
1     1     ftlm 1.0000  NA 2.442 [+2.104,+2.900]
2     4     pcci 1.0000  NA 2.088 [+1.763,+2.391]
3     3     rbci 0.9558  NA 0.709 [+0.369,+1.051]
4    10   v.stlm 0.0356  NA 0.197 [-0.137,+0.529]
5     6   v.satl 0.0325  NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression.

如您所见, 已经确定了五个最佳预测因子 (ftlm, pcci, rbci, v.stlm, v.satl)。它们位于前十名, 我们之前已经确定, 但那时是以不同的顺序和其它重要性权重。由于我们已经有了一个模型, 我们来检查一下验证和测试集合的结果。

验证集合

#-----------------
evalq({
  val <- DTTanh.n$val %>% targ.int() %>%
    as.matrix()
  y = val[ ,ncol(val)] %>% as.vector()
  pr <- predict(fit, X = val[ ,-ncol(val)] , 
                Z = NULL)
  
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics

   
      0   1
  0 347 204
  1 137 312
                                          
               Accuracy : 0.659           
                 95% CI : (0.6287, 0.6884)
    No Information Rate : 0.516           
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.3202          
 Mcnemar's Test P-Value : 0.0003514       
                                          
            Sensitivity : 0.7169          
            Specificity : 0.6047          
         Pos Pred Value : 0.6298          
         Neg Pred Value : 0.6949          
             Prevalence : 0.4840          
         Detection Rate : 0.3470          
   Detection Prevalence : 0.5510          
      Balanced Accuracy : 0.6608          
                                          
       'Positive' Class : 0  

结果并不令人印象深刻。测试集合:

evalq({
  test <- DTTanh.n$test %>% targ.int() %>%
    as.matrix()
  y = test[ ,ncol(test)] %>% as.vector()
  pr <- predict(fit, X = test[ ,-ncol(test)] , 
                Z = NULL)
  
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics

   
      0   1
  0 270 140
  1 186 404
                                        
               Accuracy : 0.674         
                 95% CI : (0.644, 0.703)
    No Information Rate : 0.544         
    P-Value [Acc > NIR] : < 2e-16       
                                        
                  Kappa : 0.3375        
 Mcnemar's Test P-Value : 0.01269       
                                        
            Sensitivity : 0.5921        
            Specificity : 0.7426        
         Pos Pred Value : 0.6585        
         Neg Pred Value : 0.6847        
             Prevalence : 0.4560        
         Detection Rate : 0.2700        
   Detection Prevalence : 0.4100        
      Balanced Accuracy : 0.6674        
                                        
       'Positive' Class : 0  

结果几乎相同。这意味着模型未经重新训练并生成更好的数据。

所以, 根据 varbvs, 最好的是 ftlm, pcci, rbci, v.stlm, v.satl。 

2.3. 神经网络

当我们正在研究神经网络时, 我们来测试神经网络中哪些预测因子将是最重要的选择。

我们将使用 FCNN4R 软件包, 它为 FCNN C++ 函数库的核心程序提供接口。FCNN 基于神经网络的全新表示, 这意味着效率, 模块化和可扩展性。FCNN4R 启用标准学习 (反向传播, Rprop, 模拟退火, 随机梯度) 和修剪算法 (最小量值, 最优脑外科医生), 但我认为这是一个高效的计算引擎。

用户可以使用快速梯度方法和恢复网络的功能轻松实现其算法 (去除权重和过多的神经元, 重新排列输入数据并组合网络)。

网络可以导出到 C 函数, 以便能够集成到任何程序解决方案中。

创建一个含有两个隐藏层的完全连接的网络。每一层的神经元数: 输入 = 12 (预测因子数量), 输出 = 1。通过 +/-0.17 范围内的随机权重启动神经元。在神经网络的每一层 (除了输入那一层) = c ("tanh", "tanh", :sigmoid") 设置激活函数。准备 train/val/test 集合。

下面的脚本执行这一系列的动作。

require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
  mlp_rnd_weights(a = 0.17) %>% 
  mlp_set_activation(layer = c(2, 3, 4), 
  activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
                                            #"linear", "sigmoid", "sym_sigmoid",
                                            #"tanh", "sigmoid_approx",
                                            #"sym_sigmoid_approx"), 
                 slope = 0) -> Ntanh #show() 
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>%  as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env)

我们将使用 rprop 训练方法。设置常量: tol — 如果达此等级, 训练必须停止的错误, max_ep — 必须停止训练的世代数, l2reg — 正则化系数。使用这些参数训练网络, 并直观评估网络和训练错误。

evalq({
  tol <- 1e-1
  max_ep = 1000
  l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh, 
                          input = train[ ,-ncol(train)], 
                          output = train[ ,ncol(train)] %>% as.matrix(),
                          tol_level = tol, 
                          max_epochs = max_ep, 
                          l2reg = l2reg,
                          u = 1.2, d = 0.5, 
                          gmax = 50, gmin = 1e-06, 
                          report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l", 
     main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))

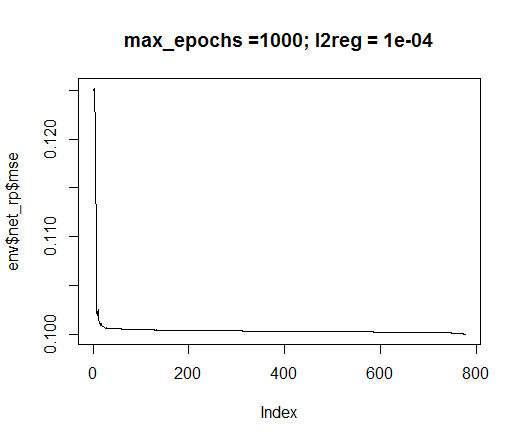
图例.35. 神经网络训练错误

evalq(mlp_plot(net_rp$net, FALSE), envir = env)

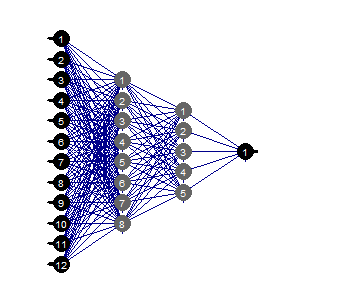
图例.36. 神经网络的结构

修剪

修剪最小值是一种简单易用的算法。在此, 绝对值最小的权重在每一步中均被关闭。该算法几乎每一步均需要网络中继, 并给出次优结果。

evalq({
  tol <- 1e-1
  max_ep = 1000
  l2reg = 0.0001
  mlp_prune_mag(net_rp$net, 
                input = train[ ,-ncol(train)], 
                output = train[ ,ncol(train)] %>% as.matrix(),
                tol_level = tol,  
                max_reteach_epochs = max_ep, 
                report = FALSE,
                plots = TRUE) -> net_rp_prune
  
}, env)

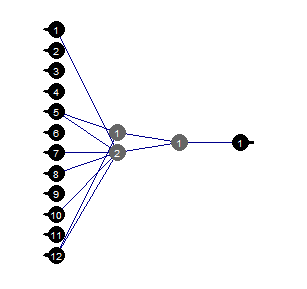
图例.37. 修剪神经网络

我们可以看到, 神经网络带有 某种结构, 初始设置, 激活函数和错误学习, 而结构为 (12, 2, 1, 1) 的神经网络就足够了。神经网络选择哪些预测因子？

evalq(
  best <- train %>% tbl_df %>%  select(c(1,5,7,8,10,12)) %>% colnames(),
           env)
env$best
[1] "ftlm"   "v.fatl" "v.rftl" "v.rstl" "v.stlm"
[6] "v.pcci"

v.rstl 和 v.pcci变量在早前定义的九个最好变量中不存在。

我想强调的是, 在此我们表明神经网络可以独立自动地选择重要的预测因子。这种选择不仅取决于预测因子, 而且取决于网络的结构和参数。

实验快乐！

结束语

在以后的部分中, 我们将讨论如何从集合中删除噪声的示例, 如何减小输入的大小, 以及将原始数据分隔成 训练/验证/测试的方式将会产生什么影响。

应用

1. 您可从 Git /Part_II 下载 FeatureTransformation.R, FeatureSelect.R, FeatureSelect_analitic.R FeatureSelect_NN.R 脚本, 以及本文 RData 的 Part_1 脚本示意图。