概述
MetaTrader 5 交易平台中的策略测试器只提供两种优化选项: 参数完整搜索和遗传算法。 本文提出了一种交易策略优化的新方法 — 模拟退火。 该方法的算法, 其实现和集成到任何智能交易系统的方方面面在此均加以考虑。 接下来, 使用移动均线 EA 对其性能进行测试, 并将模拟退火方法得到的结果与遗传算法的结果进行比较。
模拟退火算法
模拟退火是随机优化的一种方法。 它顺序随机搜索目标函数的最优值。
模拟退火算法基于模拟物质中晶体结构的形成。 物质 (例如金属) 晶格中的原子可以进入具有较低能级的状态, 或者随着温度降低而保持原位。 进入新状态的概率与温度成正比。 目标函数的最小值或最大值可以通过模拟这种过程找到。
搜索目标函数最优值的过程可用下面的方式表述:

图例 1. 寻找目标函数的最佳值
在图例 1 当中, 目标函数的值呈现为沿着不平坦表面滚动的球。 蓝色球代表目标函数的初始值, 绿色代表最终值 (全局最小值)。 红球是函数局部最小处的数值。 模拟退火算法试图找到目标函数的全局极值, 并避免在局部极值上 "卡壳"。 当接近全局极值时, 超过局部极值的概率降低。
我们来研究模拟退火算法的步骤。 为了清晰起见, 将考虑搜索目标函数的全局最小值。 模拟退火有三种主要的实现选项: 玻尔兹曼退火, 柯西退火 (快速退火), 超快退火。 它们之间的区别在于新点位 x(i) 的生成方法和温度递减的规则。
这里是算法中使用的变量:
- Fopt — 目标函数的最优值;
- Fbegin — 目标函数的初始值;
- x(i) — 当前点位的值 (目标函数的值取决于此参数);
- F(x(i)) — 点位 x(i) 的目标函数值;
- i — 迭代计数器;
- T0 — 初始温度;
- T — 当前温度;
- Xopt — 在达到目标函数最佳值时的参数值;
- Tmin — 最低温度值;
- Imax — 最大迭代次数。
退火算法由以下步骤组成:
- 步骤 0. 算法初始化: Fopt = Fbegin, i=0, T=T0, Xopt = 0。
- 步骤 1. 随机选择当前点 x(0) 并计算给定点位 F(x(0)) 目标函数。 如果 F(x(0))<Fbegin, 则 Fopt=F(x(0))。
- 步骤 2. 新点位 x(i) 的生成。
- 步骤 3. 目标函数 F(x(i)) 的计算。
- 步骤 4. 检查新状态转换。 接下来, 考虑两种改编算法:
- a). 如果发生新状态的转换, 降低当前温度并转至步骤 5, 否则转至步骤 2。
- b). 无论检查新状态的转换结果如何, 降低当前温度并转至步骤 5。
- 步骤 5. 检查算法退出标准 (温度达到 Tmin 的最小值, 或达到指定迭代次数 Imax)。 如果不符合算法退出标准: 增加迭代计数器 (i=i+1) 并转至步骤 2。
我们来更详尽地研究每个步骤, 以便寻找目标函数的最小值。
步骤 0. 初始值分配给变量, 在算法操作期间将修改其值。
步骤 1. 当前点位是需要优化的 EA 参数值。 可以有若干个这样的参数。 每个参数都分配一个随机值, 它们均匀地分布在 Pmin 到 Pmax 区间内, 指定步长为 Step (Pmin, Pmax 是优化参数的最小值和最大值)。 在测试器中按照生成的参数 EA 执行一次运算, 并计算目标函数 F(x(0)) 的值, 这是 EA 参数优化的结果 (指定优化标准的值)。 如果 F(x(0))<Fbegin, Fopt=F(x(0))。
步骤 2. 新点位的生成, 取决于根据表 1 中的公式实现的算法变体的执行结果。
表 1
| 算法实现的变体 | 计算新的初始点位的公式 |
|---|---|
| 玻尔兹曼退火 | |
| 柯西退火 (快速退火) | |
| 超快退火 | 变量  |
步骤 3. EA 测试使用步骤 2 中生成的参数执行。 目标函数 F(x(i)) 按照所选优化标准分配数值。
步骤 4. 新状态转换的检查如下进行:
- 步骤 1. 如果 F(x(i))<Fopt, 移至新状态 Xopt =x(i), Fopt=F(x(i)), 否则转至步骤 2。
- 步骤 2. 生成一个随机变量 a, 均匀分布在 [0,1) 区间。
- 步骤 3. 计算转换到新状态的概率:
- 步骤 4. 如果 P>a, 移至新状态 Xopt =x(i), Fopt=F(x(i)); 否则, 如果修改 а) 所选算法, 转至步骤 2。
- 步骤 5. 使用表 2 中的公式降低当前温度。
表 2
| 算法实现的变体 | 降低温度的公式 |
|---|---|
| 玻尔兹曼退火 |
|
| 柯西退火 (快速退火) | |
| 超快退火 | 其中 c(i)>0 并按以下公式计算: 为了简化算法配置, 当算法运行时 m(i) 和 p(i) 的数值不会变化: m(i)=const, p(i) = const |
步骤 5. 当满足以下条件时退出该算法: T(i)<=Tmin 或 i=Imax。
- 如果您选择的温度变化规则令温度快速下降, 则最好在 T(i)<= Tmin 时终止算法, 而不必等待所有迭代完成。
- 如果温度下降非常缓慢, 则一旦达到最大迭代次数, 算法将退出。 在这种情况下, 可能需要更改温度降低规则的参数。
所有算法步骤均已详加研究, 我们来以 MQL5 实现它。
算法的实现
我们来研究算法的实现, 以及将其集成到含有可优化参数的智能系统之中的过程。
算法的实现需要两个新类, 应该包含在优化的智能交易系统中:
- AnnealingMethod.mqh 类 — 包含一组算法分步实现的方法;
- FrameAnnealingMethod.mqh 类 — 包含在终端图表中显示操作图形界面的方法。
此外, 算法的操作需要将附加代码包含在 OnInit 函数中, 并将函数 OnTester, OnTesterInit, OnTesterDeInit, OnTesterPass 添加到 EA 代码中。 将算法集成到智能系统的过程如图例 2 所示。
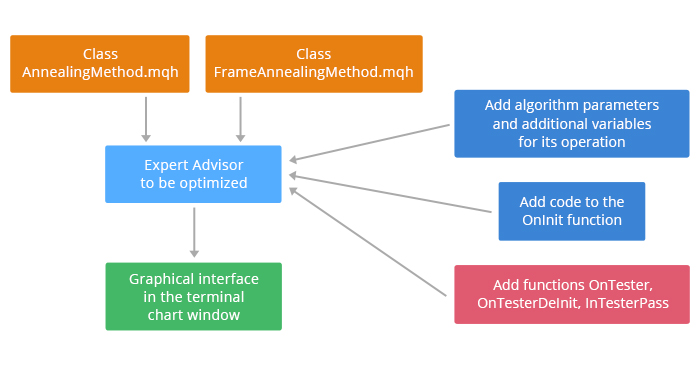
图例 2. 将算法包含在智能交易系统中
我们现在来描述 AnnealingMethod 和 FrameAnnealingMethod 类。
AnnealingMethod 类
此处是 AnnealingMethod 类的描述和其方法的更多细节。
#include "Math/Alglib/alglib.mqh" //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class AnnealingMethod { private: CAlglib Alg; // 用于处理 Alglib 函数库方法的类实例 CHighQualityRandStateShell state; // 用于生成随机数的类实例 public: AnnealingMethod(); ~AnnealingMethod(); struct Input // 用于处理 EA 参数的结构 { int num; double Value; double BestValue; double Start; double Stop; double Step; double Temp; }; uint RunOptimization(string &InputParams[],int count,double F0,double T); uint WriteData(Input &InpMass[],double F,int it); uint ReadData(Input &Mass[],double &F,int &it); bool GetParams(int Method,Input &Mass[]); double FindValue(double val,double step); double GetFunction(int Criterion); bool Probability(double E,double T); double GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2); double UniformValue(double min,double max,double step); bool VerificationOfVal(double start,double end,double val); double Distance(double a,double b); };
ALGLIB 函数库中涉及处理随机变量的函数将用于 AnnealingMethod 类方法的操作。 该函数库是标准 MetaTrader 5 软件包的一部分, 位于 "Include/Math/Alglib" 文件夹中, 如下所示:
图例 3. ALGLIB 函数库
Private 模块包含用于处理 ALGLIB 函数的 CAlglib 和 CHighQualityRandStateShell 类实例的声明。
若要使用 EA 的优化参数, 创建了 Input 结构, 其中保存:
- 参数表号, num;
- 当前参数值, Value;
- 最佳参数值, BestValue;
- 初始值, Start;
- 终值, Stop;
- 参数变化增量, Step;
- 给定参数的当前温度, Temp.
我们研究一下 AnnealingMethod.mqh 类的方法。
RunOptimization 方法
设计用于初始化模拟退火算法。 方法的代码:
uint AnnealingMethod::RunOptimization(string &InputParams[],int count,double F0,double T) { Input Mass[]; ResetLastError(); bool Enable=false; double Start= 0; double Stop = 0; double Step = 0; double Value= 0; int j=0; Alg.HQRndRandomize(&state); // 初始化 for(int i=0;i<ArraySize(InputParams);i++) { if(!ParameterGetRange(InputParams[i],Enable,Value,Start,Step,Stop)) return GetLastError(); if(Enable) { ArrayResize(Mass,ArraySize(Mass)+1); Mass[j].num=i; Mass[j].Value=UniformValue(Start,Stop,Step); Mass[j].BestValue=Mass[j].Value; Mass[j].Start=Start; Mass[j].Stop=Stop; Mass[j].Step=Step; Mass[j].Temp=T*Distance(Start,Stop); j++; if(!ParameterSetRange(InputParams[i],false,Value,Start,Stop,count)) return GetLastError(); } else InputParams[i]=""; } if(j!=0) { if(!ParameterSetRange("iteration",true,1,1,1,count)) return GetLastError(); else return WriteData(Mass,F0,1); } return 0; }
方法的输入参数:
- 包含智能交易系统所有参数名称的字符串数组, InputParams[];
- 算法迭代次数, count;
- 目标函数的初始值, F0;
- 初始温度, T.
RunOptimization 方法的工作原理如下:
- 它搜索需要优化的 EA 参数。 这些参数应在策略测试器的 "参数" 选项卡中 "勾选":
- 每次找到的参数值保存在 Input 结构类型的 Mass[] 数组中, 且参数被排除在优化之外。 结构数组 Mass[] 存储:
- 参数编号;
- 由 UniformValue 方法生成的参数值 (如下所示);
- 参数的最大 (开始) 和最小 (终止) 值;
- 参数值变化增量, (步长);
- 初始温度公式计算: T*Distance(Start,Stop); Distance 方法将在以下讨论。
- 搜索完成后, 所有参数都被禁用, 并且 iteration 参数被激活, 其决定了算法迭代的次数;
- Mass[] 数组的值, 目标函数和迭代次数使用 WriteData 方法写入一个二进制文件。
WriteData 方法
设计用于将参数数组, 目标函数值和迭代次数写入文件。
WriteData 方法的代码:
uint AnnealingMethod::WriteData(Input &Mass[],double F,int it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_WRITE|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileWriteArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteDouble(file_handle,F)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteInteger(file_handle,it)<=0) {FileClose(file_handle); return GetLastError();} } else return GetLastError(); FileClose(file_handle); return 0; }
使用函数 FileWriteArray, FileWriteDouble 和 FileWriteInteger 函数将数据写入 data.bin 文件。 该方法实现了多次尝试访问 data.bin 文件的功能。 这样做是为了避免在访问文件时恰好文件被另一个进程占用从而发生错误。
ReadData 方法
设计用于读取参数数组, 目标函数值和文件中的迭代次数。 ReadData 方法的代码:
uint AnnealingMethod::ReadData(Input &Mass[],double &F,int &it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_READ|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileReadArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} F=FileReadDouble(file_handle); it=FileReadInteger(file_handle); } else return GetLastError(); FileClose(file_handle); return 0; }
使用 FileReadArray, FileReadDouble, FileReadInteger 函数按照 WriteData 方法的相同写入顺序从文件中读取数据。
GetParams 方法
GetParams 方法设计用于计算智能系统已优化参数的新值, 以便用于 EA 的下一次运行。 表 1 中提供了计算智能系统已优化参数新值的公式。
方法的输入参数:
- 算法实现的变体 (玻尔兹曼退火, 柯西退火或超快退火);
- Input 类型的已优化参数数组;
- 系数 CoeffTmin 用于计算终止算法的最低温度。
GetParams 方法的代码:
bool AnnealingMethod::GetParams(int Method,Input &Mass[],double CoeffTmin) { double delta=0; double x1=0,x2=0; double count=0; Alg.HQRndRandomize(&state); // 初始化 switch(Method) { case(0): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count= 0; break; } count++; delta=Mass[i].Temp*Alg.HQRndNormal(&state); delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } // while((delta<Mass[i].Start) || (delta>Mass[i].Stop)); while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(1): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; Alg.HQRndNormal2(&state,x1,x2); delta=Mass[i].Temp*x1/x2; delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(2): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; x1=Alg.HQRndUniformR(&state); if(x1-0.5>0) delta=Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); else { if(x1==0.5) delta=0; else delta=-Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); } delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } default: { Print("退火方法选择错误"); return false; } } return true; }
我们来更详尽地研究该方法。
该方法有一个 switch 操作符, 可根据所选算法实现的变体开始计算新参数值。 只有当前温度高于最小值时, 才会计算新的参数值。 最低温度通过以下公式计算: CoeffTmin*Distance(Start,Stop), 其中 Start 和 Stop 是参数的最小值和最大值。 Distance 方法将在下面研究。
调用 CAlglib 类 的 HQRndRandomize 方法来初始化处理随机数的方法。
Alg.HQRndRandomize(&state);
CAlglib 类 的 HQRndNormal 函数用于计算标准正态分布值:
Alg.HQRndNormal(&state);
柯西分布可以用各种方式建模, 例如, 通过正态分布或反函数。 使用以下比率:
C(0,1)=X1/X2, 其中 X1 和 X2 是正态分布的独立变量, X1,X2 = N(0,1)。 CAlglib 类 的 HQRndNormal2 函数用于生成两个正态分布变量:
Alg.HQRndNormal2(&state,x1,x2);
正态分布数值的自变量存储在 x1, x2 中。
CAlglib 类 的 HQRndUniformR(&state) 方法生成一个均匀分布在从 0 至 1 区间的随机数字:
Alg.HQRndUniformR(&state);
使用 FindValue 方法 (下述), 计算出的参数值会四舍五入到指定步长以便用于修改参数。 如果计算出的参数值超过参数变化范围 (由 VerificationOfVal 方法检查), 则重新计算。
FindValue 方法
每个已优化的参数值应按照指定步长骤进行更改。 在 GetParams 中生成的新数值可能不符合此条件, 并且需要四舍五入为指定步长的倍数。 这由 FindValue 方法完成。 方法的输入参数: 要四舍五入的值 (val) 以及参数变化的步长 (step)。
此处是 FindValue 方法的代码:
double AnnealingMethod::FindValue(double val,double step) { double buf=0; if(val==step) return val; if(step==1) return round(val); else { buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step); if(MathAbs(val)-buf*MathAbs(step)>=MathAbs(step)/2) { if(val<0) return -(buf + 1)*MathAbs(step); else return (buf + 1)*MathAbs(step); } else { if(val<0) return -buf*MathAbs(step); else return buf*MathAbs(step); } } }
我们来更详尽地研究该方法。
如果该步长等于该参数的输入值, 则函数返回该值:
if(val==step) return val;
如果步长为 1, 参数的输入值只需要四舍五入为整数:
if(step==1) return round(val);
否则, 请在参数输入值中查找步长数字:
buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);
并计算一个新值, 这是步长的倍数。
GetFunction 方法
GetFunction 方法设计用于获取目标函数的新值。 该方法的输入参数是用户定义的优化标准。
根据选定的计算模式, 目标函数从测试结果计算出的统计参数中取得一个或若干个值。 方法的代码:
double AnnealingMethod::GetFunction(int Criterion) { double Fc=0; switch(Criterion) { case(0): return TesterStatistics(STAT_PROFIT); case(1): return TesterStatistics(STAT_PROFIT_FACTOR); case(2): return TesterStatistics(STAT_RECOVERY_FACTOR); case(3): return TesterStatistics(STAT_SHARPE_RATIO); case(4): return TesterStatistics(STAT_EXPECTED_PAYOFF); case(5): return TesterStatistics(STAT_EQUITY_DD);//min case(6): return TesterStatistics(STAT_BALANCE_DD);//min case(7): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_PROFIT_FACTOR); case(8): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_RECOVERY_FACTOR); case(9): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_SHARPE_RATIO); case(10): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_EXPECTED_PAYOFF); case(11): { if(TesterStatistics(STAT_BALANCE_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_BALANCE_DD); else return TesterStatistics(STAT_PROFIT); } case(12): { if(TesterStatistics(STAT_EQUITY_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_EQUITY_DD); else return TesterStatistics(STAT_PROFIT); } case(13): { // 例如, 指定自定义标准 return TesterStatistics(STAT_TRADES)*TesterStatistics(STAT_PROFIT); } default: return -10000; } }
从代码中您可以看出, 该方法实现了 14 种目标函数的计算方法。 也就是说, 用户可以通过各种统计参数优化智能系统。 统计参数的详细描述可在 文档 中找到。
Probability 方法
Probability 方法旨在识别新状态的转换。 方法的输入参数: 目标函数 (E) 的和温度 (T) 当前值与前值的差别。 方法的代码:
bool AnnealingMethod::Probability(double E,double T) { double a=Alg.HQRndUniformR(&state); double res=exp(-E/T); if(res<=a) return false; else return true; }
方法生成一个随机变量 а, 均匀分布在 [0,1) 区间:
a=Alg.HQRndUniformR(&state);
将得到的值与表达式 exp(-E/T) 进行比较。 如果 a>exp(-E/T), 那么该方法返回 true (转换到新状态)。
GetT 方法
GetT 方法计算新的温度值。 方法的输入参数:
- 算法实现的变体 (玻尔兹曼退火, 柯西退火或超快退火);
- 温度初始值, T0;
- 温度前值, Tlast;
- 迭代次数, it;
- 已优化参数数量, D;
- 超快退火的辅助参数 p1 和 p2。
方法的代码:
double AnnealingMethod::GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2) { int Iteration=0; double T=0; switch(Method) { case(0): { if(Tlast!=T0) Iteration=(int)MathRound(exp(T0/Tlast)-1)+1; else Iteration=1; if(Iteration>0) T=T0/log(Iteration+1); else T=T0; break; } case(1): { if(it!=1) Iteration=(int)MathRound(pow(T0/Tlast,D))+1; else Iteration=1; if(Iteration>0) T=T0/pow(Iteration,1/D); else T=T0; break; } case(2): { if((T0!=Tlast) && (-p1*exp(-p2/D)!=0)) Iteration=(int)MathRound(pow(log(Tlast/T0)/(-p1*exp(-p2/D)),D))+1; else Iteration=1; if(Iteration>0) T=T0*exp(-p1*exp(-p2/D)*pow(Iteration,1/D)); else T=T0; break; } } return T; }
该方法基于算法实现的变体以及表 2 中的公式计算新的温度值。 考虑到算法的实现在发生新状态转变时仅增加温度, 使用先前的温度值 Tlast 来计算当前迭代。 因此, 当调用该方法时, 当前温度下降, 而不管算法的当前迭代如何。
UniformValue 方法
UniformValue 方法会根据最小值, 最大值和步长生成优化参数的随机值。 该方法仅在算法初始化期间使用, 来生成优化参数的初始值。 方法的输入参数:
- 最大参数值, max;
- 最小参数值, min;
- 参数变化的步长, step.
方法的代码:
double AnnealingMethod::UniformValue(double min,double max,double step) { Alg.HQRndRandomize(&state); //初始化 if(max>min) return FindValue(Alg.HQRndUniformR(&state)*(max-min)+min,step); else return FindValue(Alg.HQRndUniformR(&state)*(min-max)+max,step); }
VerificationOfVal 方法
VerificationOfVal 检查 (val) 变量的指定值是否超出范围 (start,end)。 该方法用在 GetParams 方法当中。
方法的代码:
bool AnnealingMethod::VerificationOfVal(double start,double end,double val) { if(start<end) { if((val>=start) && (val<=end)) return true; else return false; } else { if((val>=end) && (val<=start)) return true; else return false; } }
该方法考虑到参数更改步长可能为负, 因此它会检查条件 "start<end"。
Distance 方法
Distance 方法计算两个参数 (a 和 b) 之间的距离, 且在算法中用于计算参数变化范围, 初始值为 a, 最终值为 b。
方法的代码:
double AnnealingMethod::Distance(double a,double b) { if(a<b) return MathAbs(b-a); else return MathAbs(a-b); }
FrameAnnealingMethod 类
FrameAnnealingMethod 类用于在终端窗口中显示算法执行过程。 这里是 FrameAnnealingMethod 类的描述:
#include <SimpleTable.mqh> #include <Controls\BmpButton.mqh> #include <Controls\Label.mqh> #include <Controls\Edit.mqh> #include <AnnealingMethod.mqh> //+------------------------------------------------------------------+ //| 类用于优化结果的输出 | //+------------------------------------------------------------------+ class FrameAnnealingMethod { private: CSimpleTable t_value; CSimpleTable t_inputs; CSimpleTable t_stat; CBmpButton b_playbutton; CBmpButton b_backbutton; CBmpButton b_forwardbutton; CBmpButton b_stopbutton; CLabel l_speed; CLabel l_stat; CLabel l_value; CLabel l_opt_value; CLabel l_temp; CLabel l_text; CLabel n_frame; CEdit e_speed; long frame_counter; public: //--- 构造函数/析构函数 FrameAnnealingMethod(); ~FrameAnnealingMethod(); //--- 策略测试器的事件 void FrameTester(double F,double Fbest,Input &Mass[],int num,int it); void FrameInit(string &SMass[]); void FrameTesterPass(int cr); void FrameDeinit(void); void FrameOnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam,int cr); uint FrameToFile(int count); };
FrameAnnealingMethod 类包含以下方法:
- FrameInit — 在终端窗口中创建一个图形界面;
- FrameTester — 添加当前数据帧;
- FrameTesterPass — 将当前数据帧输出到终端窗口;
- FrameDeInit — 显示有关智能系统完成优化的文字信息;
- FrameOnChartEvent — 处理按钮按下事件;
- FrameToFile — 将测试结果保存到文本文件中。
方法的代码在 FrameAnnealingMethod.mqh 文件中提供 (已附加到文章中)。 请注意, SimpleTable.mqh 文件 (已附加到文章) 是 FrameAnnealingMethod 类中的方法工作所必需的。 将其放置于 MQL5/Include。 该文件已被 项目 中采纳, 并补充了 GetValue 方法, 该方法允许从表格单元读取值。
以下是使用 FrameAnnealingMethod 类在终端窗口中创建的示例图形界面。
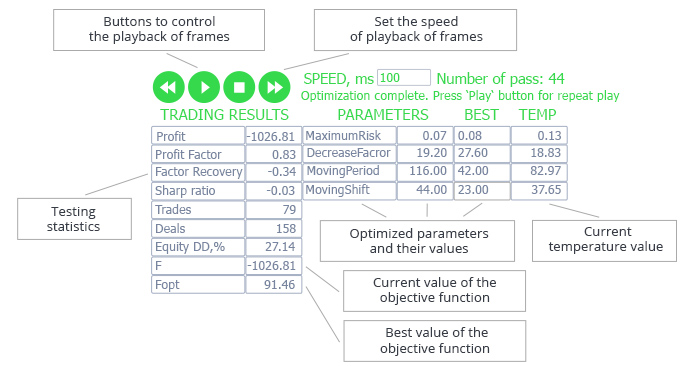
图例 4. 用于演示算法操作的图形界面
表中左侧包含由策略测试器根据当前运行结果生成的统计参数, 以及目标函数的当前值和最佳值 (在本例中, 选择净利润作为目标函数)。
已优化的参数位于表格的右侧: 参数名称, 当前值, 最佳值, 当前温度。
在表格上方, 在算法执行完成后, 有按钮可控制帧的回放。 因此, 智能系统优化完成后, 您可指定速度重播它。 这些按钮可让您停止回放, 或从中断的位置再次开始播放。 播放速度可以使用按钮调整, 也可以手动设置。 当前运行的编号显示在速度值的右侧。 算法操作的辅助信息显示如下。
AnnealingMethod 和 FrameAnnealingMethod 类已经研究完毕。 现在我们继续使用基于移动平均的智能交易系统来测试算法。
测试基于移动平均的 EA 算法
准备测试算法的 EA
应修改智能系统的代码以便运行该算法:
- 包括 AnnealingMethod 类和 FrameAnnealingMethod 类, 并声明算法操作用到的辅助变量;
- 将代码添加到 OnInit 函数, 添加函数 OnTester, OnTesterInit, OnTesterDeInit, OnTesterPass, OnChartEvent。
添加的代码不影响 EA 操作, 它仅当 EA 在策略测试器中优化时才运行。
所以, 让我们开始吧。
将 OnTesterInit 函数生成的初始参数包含于该文件:
#property tester_file "data.bin"
包括 AnnealingMethod 和 FrameAnnealingMethod 类:
// 包含类 #include <AnnealingMethod.mqh> #include <FrameAnnealingMethod.mqh>
声明所包含类的实例
AnnealingMethod Optim; FrameAnnealingMethod Frame;
声明算法操作的辅助变量:
Input InputMass[]; // 输入参数数组 string SParams[]; // 输入参数名称数组 double Fopt=0; // 函数的最佳值 int it_agent=0; // 用于测试代理的算法迭代次数 uint alg_err=0; // 出错次数
模拟退火算法将在其工作过程中修改优化参数的值。 出于此目的, EA 的输入参数将被重命名:
double MaximumRisk_Optim=MaximumRisk; double DecreaseFactor_Optim=DecreaseFactor; int MovingPeriod_Optim=MovingPeriod; int MovingShift_Optim=MovingShift;
在 EA 的所有函数当中, 替换参数: MaximumRisk 为 MaximumRisk_Optim, DecreaseFactor 为 DecreaseFactor_Optim, MovingPeriod 为 MovingPeriod_Optim, MovingShift 为 MovingShift_Optim。
以下是算法操作的配置变量:
sinput int iteration=50; // 迭代次数 sinput int method=0; // 0 - 玻尔兹曼退火, 1 - 柯西退火, 2 - 超快退火 sinput double CoeffOfTemp=1; // 初始温度的比例系数 sinput double CoeffOfMinTemp=0; // 最低温度系数 sinput double Func0=-10000; // 目标函数的初始值 sinput double P1=1; // 超快退火的附加参数, p1 sinput double P2=1; // 超快退火的附加参数, p2 sinput int Crit=0; // 目标函数计算方法 sinput int ModOfAlg=0; // 算法修改类型 sinput bool ManyPoint=false; // 多点优化
算法的参数在操作期间不应改变; 因此, 所有变量都使用 sinput 标识符声明。
表 3 解释了所声明变量的用途。
表 3
| 变量名 | 目的 |
|---|---|
| 迭代 | 定义算法的迭代次数 |
| 方法 | 定义算法实现的变体: 0 — 玻尔兹曼退火, 1 — 柯西退火, 2 — 超快退火 |
| CoeffOfTemp | 定义由公式计算出的初始温度系数: T0=CoeffOfTemp*Distance(Start,Stop), 此处 Start, Stop 是最小和最大参数值, Distance 是 AnnealingMethod 类 (如上表述) 中的一个方法 |
| CoeffOfMinTemp | 定义用于设置终止算法的最低温度系数。 最高温度的计算与初始温度相似: Tmin=CoeffOfMinTemp*Distance(Start,Stop), 此处 Start, Stop 是参数的最小值和最大值, Distance 是 AnnealingMethod 类 (如上表述) 中的一个方法 |
| Func0 | 目标函数的初始值 |
| P1,P2 | 用于计算超快退火中当前温度的参数 (见表 2) |
| Crit | 优化标准: 0 — 净利润总额; 1 — 盈利因子; 2 — 恢复因子; 3 — 锋锐比率; 4 — 预期收益; 5 — 最大净值回撤; 6 — 最大余额回撤; 7 — 净利润总额 + 盈利因子; 8 — 净利润总额 + 恢复因子; 9 — 净利润总额 + 锋锐比率; 10 — 净利润总额 + 预期收益; 11 — 净利润总额 + 最大余额回撤; 12 — 净利润总额 + 最大净值回撤; 13 — 自定义标准。 目标函数在 AnnealingMethod 类的 GetFunction 函数中进行计算 |
| ModOfAlg | 算法修改的类型: 0 - 如果已经发生新状态转换, 降低当前温度并继续执行算法完成检查, 否则, 计算优化参数的新值; 1 - 无论检查新状态转换的结果如何, 降低当前温度并继续检查算法完成 |
| ManyPoint | true —为每个测试代理生成不同的优化参数初始值, false — 为每个测试代理生成相同的优化参数初始值 |
将代码添加到 OnInit 函数的开头:
//+------------------------------------------------------------------+ //| 模拟退火 | //+------------------------------------------------------------------+ if(MQL5InfoInteger(MQL5_OPTIMIZATION)) { // 打开文件并读取数据 // if(FileGetInteger("data.bin",FILE_EXISTS,false)) // { alg_err=Optim.ReadData(InputMass,Fopt,it_agent); if(alg_err==0) { // 若是第一次运行, 如果从不同点位执行搜索, 则随机生成参数 if(Fopt==Func0) { if(ManyPoint) for(int i=0;i<ArraySize(InputMass);i++) { InputMass[i].Value=Optim.UniformValue(InputMass[i].Start,InputMass[i].Stop,InputMass[i].Step); InputMass[i].BestValue=InputMass[i].Value; } } else Optim.GetParams(method,InputMass,CoeffOfMinTemp); // generate new parameters // 填充智能交易系统的参数 for(int i=0;i<ArraySize(InputMass);i++) switch(InputMass[i].num) { case (0): {MaximumRisk_Optim=InputMass[i].Value; break;} case (1): {DecreaseFactor_Optim=InputMass[i].Value; break;} case (2): {MovingPeriod_Optim=(int)InputMass[i].Value; break;} case (3): {MovingShift_Optim=(int)InputMass[i].Value; break;} } } else { Print("读文件错误"); return(INIT_FAILED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
我们来详查代码。 添加的代码仅在策略测试器的优化模式下执行:
if(MQL5InfoInteger(MQL5_OPTIMIZATION))
接下来, 从 AnnealingMethod 类的 RunOptimization 方法生成的 data.bin 文件读取数据。 此方法在 OnTesterInit 函数中调用, 函数代码将在下面展示。
alg_err=Optim.ReadData(InputMass,Fopt,it_agent);
如果读取的数据没有错误 (alg_err=0), 则执行检查以确定算法是否处于第一次迭代 (Fopt==Func0), 否则 EA 初始化失败并显示错误。 若是第一次迭代, 且 ManyPoint=true, 则生成优化参数的初始值并存储在 Input 类型结构的 InputMass 当中 (在 AnnealingMethod 类中已描述), 否则调用 GetParams 方法
Optim.GetParams(method,InputMass,CoeffOfMinTemp);// 生成新参数
并填充参数值 MaximumRisk_Optim, DecreaseFactor_Optim, MovingPeriod_Optim, MovingShift_Optim。
现在我们来研究一下 OnTesterInit 函数的代码:
void OnTesterInit() { // 填充所有 EA 参数的名称数组 ArrayResize(SParams,4); SParams[0]="MaximumRisk"; SParams[1]="DecreaseFactor"; SParams[2]="MovingPeriod"; SParams[3]="MovingShift"; // 开始优化 Optim.RunOptimization(SParams,iteration,Func0,CoeffOfTemp); // 创建图形界面 Frame.FrameInit(SParams); }
首先, 填充包含所有 EA 参数名称的字符串数组。 然后运行 RunOptimization 方法并使用 FrameInit 方法创建一个图形界面。
在指定的时间间隔内运行 EA 后, 控制将被转移到 OnTester 函数。 此处是代码:
double OnTester() { int i=0; // 循环计数器 int count=0; // 辅助变量 // 当达到最低温度时检查算法是否完成 for(i=0;i<ArraySize(InputMass);i++) if(InputMass[i].Temp<CoeffOfMinTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop)) count++; if(count==ArraySize(InputMass)) Frame.FrameTester(0,0,InputMass,-1,it_agent); // 添加一个零参数的帧, 且 id=-1 else { double Fnew=Optim.GetFunction(Crit); // 计算函数的当前值 if((Crit!=5) && (Crit!=6) && (Crit!=11) && (Crit!=12)) // 如果有必要最大化目标函数 { if(Fnew>Fopt) Fopt=Fnew; else { if(Optim.Probability(Fopt-Fnew,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } else // 如果有必要最小化目标函数 { if(Fnew<Fopt) Fopt=Fnew; else { if(Optim.Probability(Fnew-Fopt,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } // 覆盖最佳参数值 if(Fopt==Fnew) for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue=InputMass[i].Value; // 降低温度 if(((ModOfAlg==0) && (Fnew==Fopt)) || (ModOfAlg==1)) { for(i=0;i<ArraySize(InputMass);i++) InputMass[i].Temp=Optim.GetT(method,CoeffOfTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop),InputMass[i].Temp,it_agent,ArraySize(InputMass),P1,P2); } Frame.FrameTester(Fnew,Fopt,InputMass,iteration,it_agent); // 添加新帧 it_agent++; // 增加迭代计数器 alg_err=Optim.WriteData(InputMass,Fopt,it_agent); // 将新数值写入文件 if(alg_err!=0) return alg_err; } return Fopt; }
我们来更详尽地研究这个函数的代码。
- 当达到最低温度时, 它会检查算法的完成情况。 如果每个参数的温度已经达到最小值, 则添加 id=-1 的帧, 参数值不再改变。 终端窗口中的图形界面提示用户通过按下策略测试器中的 "停止" 按钮来完成优化。
- GetFunction 方法使用智能交易系统测试结果计算目标函数 Fnew 的新值。
- 依据优化标准 (见表 3), 将 Fnew 的值与 Fopt 的最佳值进行比较, 并检查新状态转换。
- 如果已经发生新状态转换, 则将优化参数的当前值设置为最佳:
for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue = InputMass[i].Value;
- 检查降低当前温度的条件。 如果满足, 则使用退火方法类的 Get 方法计算新温度。
- 添加新帧, 优化参数的值被写入文件。
OnTester 函数在 OnTesterPass 函数中添加需要进一步处理的帧。 此处是代码:
void OnTesterPass() { Frame.FrameTesterPass(Crit);// 方法显示图形界面中的帧 }
OnTesterPass 函数调用 FrameAnnealingMethod 类的 FrameTesterPass 方法, 以便在终端窗口中显示优化过程。
一旦优化完成后, 将调用 OnTesterDeInit 函数:
void OnTesterDeinit() { Frame.FrameToFile(4); Frame.FrameDeinit(); }
该函数调用 FrameAnnealingMethod 类的两个方法: FrameToFile 和 FrameDeinit。 FrameToFile 方法将优化结果写入文本文件。 此方法将 EA 参数的编号作为输入进行优化。 FrameDeinit 方法向终端窗口输出关于优化完成的消息。
优化完成后, 使用 FrameAnnealingMethod 类方法创建的图形界面允许以指定的速度播放帧。 帧的回放可以停止并重新启动。 这是通过图形界面的相应按钮完成的 (见图例 4)。 为了处理终端窗口中的事件, 已在 EA 代码中添加 OnChartEvent 方法:
void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { Frame.FrameOnChartEvent(id,lparam,dparam,sparam,Crit); // 处理图形界面的方法 }
OnChartEvent 方法调用 FrameAnnealingMethod 类的 FrameOnChartEvent 方法, 该方法管理终端窗口中帧的回放。
移动均线 EA 代码的修改到此结束。 我们开始测试算法。
测试算法
提议的模拟退火方法具有随机性 (它含计算随机变量的函数), 因此, 每次运行算法均会产生不同的结果。 若要测试算法操作并确定其优缺点, 必须多次运行智能系统优化。 这将花费相当长的时间, 因此将执行以下操作: 在 "慢速完整算法" 模式下运行优化, 保存获得的结果, 然后使用这些数据测试算法。
该算法将使用 TestAnnealing.mq5 智能交易系统 (位于本文附带的 test.zip 文件中) 进行测试。 它从包含 5 列数据的文本文件中加载由全搜索方法获得的优化结果表: 列 1-4 表示变量的值, 列 5 表示目标函数的值。 TestAnnealing 中实现的算法, 使用模拟退火方法在表中移动并查找目标函数的值。 这种测试方法可以检测完整搜索所获各种数据的模拟退火性能。
好了, 我们开始吧。 首先, 测试算法性能是通过优化智能系统的一个变量 — 移动平均周期。
使用以下初始参数在完整搜索模式下运行智能系统优化:
- 最大风控百分比 — 0.02; 衰减因子 — 3; 移动均线周期: 1 - 120, 步长: 1; 移动均线偏移 — 6。
- 区间: 01.01.2017 — 31.12.2017, 交易模式: 无延迟, 逐笔报价: 1 分钟 OHLC, 初始本金: 10000, 杠杆: 1:100, 货币: EURUSD。
- 优化将使用最大余额标准来执行。
保存结果并使用获得的数据创建一个测试文件。 文本文件中的数据将按照 "移动平均周期" 参数值的升序进行排序, 如图例 5 所示。
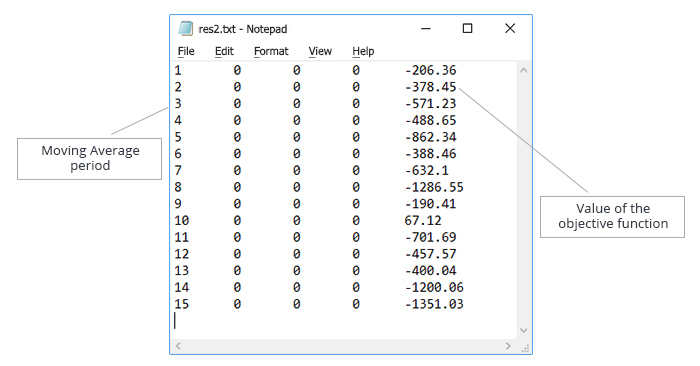
图例 5. "移动平均周期" 参数的优化。 用于测试算法操作的数据文本文件
在完整搜索模式下执行 120 次迭代。 将使用以下迭代次数来测试模拟退火算法: 30 (变体 1), 60 (变体 2), 90 (变体 3)。 此目的旨在减少迭代次数的同时测试算法的性能。
对于每个变体,在完整搜索获得的数据基础上使用模拟退火执行 10000 次优化运行。 在 TestAnnealing.mq5 智能交易系统中实现的算法, 计算目标函数最佳值的发现次数, 以及目标函数值与最佳值相差 5%, 10%, 15%, 20%, 25% 的次数。
已经获得以下测试结果。
对于该算法的 30 次迭代, 最佳值来自每次迭代中降温的超快退火:
| 距目标函数最佳值的偏离, % | 结果, % |
|---|---|
| 0 | 33 |
| 5 | 44 |
| 10 | 61 |
| 15 | 61 |
| 20 | 72 |
| 25 | 86 |
表中的数据可解释为: 在 33% 的运算中 (10,000 次运算中有 3,300次) 获得了目标函数的最佳值, 在 44% 的运算中获得 5% 的最佳值偏差, 等等。
对于该算法的 60 次迭代, 柯西退火处于领先地位, 但此处最好的变体是在新状态过渡期间降低温度。 结果如下:
| 距目标函数最佳值的偏离, % | 结果, % |
|---|---|
| 0 | 47 |
| 5 | 61 |
| 10 | 83 |
| 15 | 83 |
| 20 | 87 |
| 25 | 96 |
因此, 与完整搜索相比, 迭代次数减半, 模拟退火方法在 47% 的案例中找到了目标函数的最佳值。
对于 90 次迭代或算法, 在过渡到新状态期间玻尔兹曼退火和柯西退火随温度降低具有大致相同的结果。 这是柯西退火的结果:
| 距目标函数最佳值的偏离, % | 结果, % |
|---|---|
| 0 | 62 |
| 5 | 71 |
| 10 | 93 |
| 15 | 93 |
| 20 | 95 |
| 25 | 99 |
因此, 与完整搜索相比, 迭代计数减少了三分之一, 模拟退火方法在 62% 的情况下找到了目标函数的最佳值。 不过, 有可能获得偏差为 10-15% 的可接受结果。
测试超快退火方法, 参数 p1=1, p2=1。 增加迭代次数对所获结果的影响比之波尔兹曼退火和柯西退火的影响要大。 然而, 超快退火算法有一个特点: 改变系数 p1, p2 可以调节温度降低速度。
我们来研究超快退火的温度变化图 (图例 6):
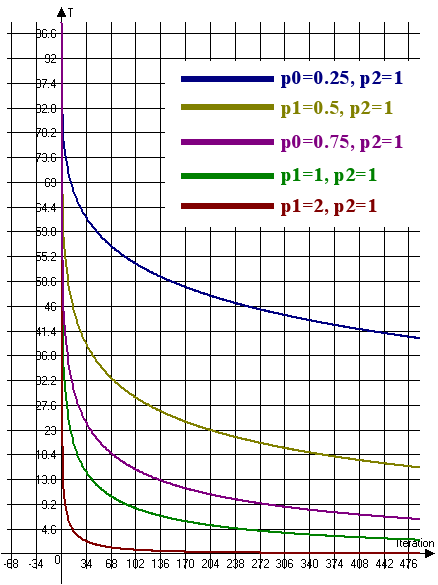
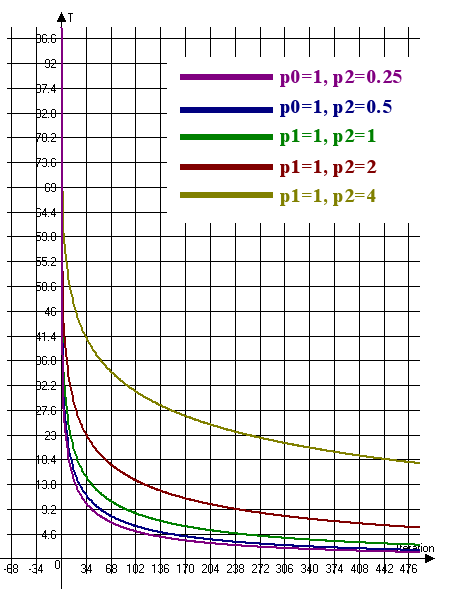
图例 6. 超快退火的温度变化图 (T0=100, n=4)
图例 6 意味着有必要增加系数 p1 并减小系数 p2 以降低温度变化率。 因此, 为了提高温度变化率, 需要降低系数 p1 并增大系数 p2。
在 60 和 90 次迭代中, 超快退火表现出最差的结果, 因为温度下降得太快。 在减小系数 p1 之后, 获得以下结果:
| 迭代次数 | p1 | p2 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|---|---|
| 60 | 0.5 | 1 | 57 | 65 | 85 | 85 | 91 | 98 |
| 90 | 0.25 | 1 | 63 | 78 | 93 | 93 | 96 | 99 |
表中显示获得的目标函数最佳值, 在 60 次迭代中为 57% 运算, 在 90 次迭代中为 63% 运算。
因此, 当优化一个参数时, 通过超快退火实现了最佳结果。 然而, 有必要根据迭代次数选择系数 p1 和 p2。
如上所述, 模拟退火算法是随机的, 所以它的操作将与随机搜索进行比较。 为此, 每次迭代都会生成一个给定步长和给定范围内的随机参数值。 在这种情况下, "移动平均周期" 参数值将以 1 为步长生成, 范围从 1 到 120。
随机搜索运行时与模拟退火的条件相同:
- 迭代次数: 30, 60, 90
- 每个变体的运行次数: 10000
随机搜索的结果显示在下表中:
| 迭代次数 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 22 | 40 | 54 | 54 | 64 | 84 |
| 60 | 40 | 64 | 78 | 78 | 87 | 97 |
| 90 | 52 | 78 | 90 | 90 | 95 | 99 |
我们来比较随机搜索和超快退火的结果。 该表显示随机搜索和相应的超快退火之间的增长百分比。 例如, 在 30 次迭代中, 超快退火算法在查找函数的最佳值时要好于随机搜索 50%。
| 迭代次数 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 50 | 10 | 12.963 | 12.963 | 12.5 | 2.381 |
| 60 | 42.5 | 1.563 | 8.974 | 8.974 | 4.6 | 1.031 |
| 90 | 21.154 | 0 | 3.333 | 3.333 | 1.053 | 0 |
该表显示增加迭代次数降低了超快退火算法的优势。
现在我们继续测试智能交易系统的两个参数 "移动平均周期" 和 "移动平均偏移" 的优化算法。 首先, 通过在策略测试器中使用以下参数运行慢速完整搜索来生成输入数据:
- 最大风控百分比 — 0.02; 衰减因子 — 3; 移动均线周期: 1-120; 移动均线偏移 - 6-60。
- 区间: 01.01.2017 — 31.12.2017, 交易模式: 无延迟, 逐笔报价: 1 分钟 OHLC, 初始本金: 10000, 杠杆: 1:100, 货币: EURUSD
- 优化将使用最大余额标准来执行。
保存结果并使用获得的数据创建一个测试文件。 文本文件中的数据按照 "移动平均周期" 参数的升序进行排序。 生成的文件如图例 7 所示。
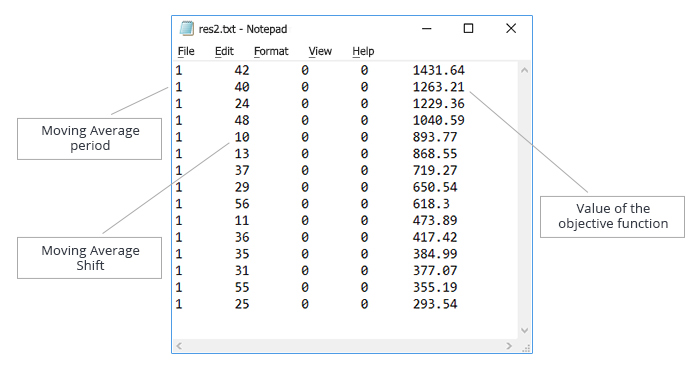
图例 7. "移动平均周期" 和 "移动平均偏移" 参数的优化。 用于测试算法操作的数据文本文件
对两个变量的慢速完整搜索在 6,600 次迭代中执行。 我们将尝试使用模拟退火来减少这个数量。 用以下迭代次数测试算法: 330, 660, 1665, 3300, 4950。 每个变体的运行次数: 10000。
测试结果如下。
330 次迭代: 柯西退火表现出良好的结果, 但最好的结果是在每次迭代中进行降温的超快退火且其系数 p1=1, p2=1 来达到的。
660 次迭代: 柯西退火的结果, 在每次迭代中降温的超快退火且其系数 p1=1, p2=1 显示出大致相同的结果。
在 1665,3300 和 4950 次迭代中, 每次迭代中进行降温的超快退火及 p1 和 p2 系数为下列值时获得最佳结果:
- 1665 次迭代: p1= 0.5, p2=1
- 3300 次迭代: p1= 0.25, p2=1
- 4950 次迭代: p1= 0.5, p2=3
表中汇总了最佳结果:
| 迭代次数 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 11 | 11 | 18 | 40 | 66 | 71 |
| 660 | 17 | 17 | 27 | 54 | 83 | 88 |
| 1665 | 31 | 31 | 41 | 80 | 95 | 98 |
| 3300 | 51 | 51 | 62 | 92 | 99 | 99 |
| 4950 | 65 | 65 | 75 | 97 | 99 | 100 |
从表中可以得出以下结论:
- 当迭代次数减少 10 倍时, 超快退火算法在 11% 的情况下找到了目标函数的最佳值; 但在 71% 的案例中, 它产生的目标函数值比之最佳值仅差 25%。
- 当迭代次数减少 2 倍时, 超快退火算法在 51% 的案例中找到了目标函数的最佳值; 但它几乎有 100% 的概率能找到比之最佳值仅差 20% 的目标函数值。
因此, 当与最佳值的微小偏差完全可以接受时, 超快退火算法可用于快速评估策略的盈利能力。
现在我们来比较超快退火算法和随机搜索。 随机搜索的结果显示在下表中:
| 迭代次数 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 5 | 5 | 10 | 14 | 33 | 42 |
| 660 | 10 | 10 | 19 | 27 | 55 | 67 |
| 1665 | 22 | 22 | 41 | 53 | 87 | 94 |
| 3300 | 40 | 40 | 64 | 79 | 98 | 99 |
| 4950 | 55 | 55 | 79 | 90 | 99 | 99 |
我们来比较随机搜索和超快退火的结果。 结果将以表格的形式呈现, 该表格显示随机搜索和相应的超快退火之间的增长百分比。
| 迭代次数 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 120 | 120 | 80 | 185.714 | 100 | 69 |
| 660 | 70 | 70 | 42.105 | 100 | 50.909 | 31.343 |
| 1665 | 40.909 | 40.909 | 0 | 50.9434 | 9.195 | 4.255 |
| 3300 | 27.5 | 27.5 | -3.125 | 16.456 | 1.021 | 0 |
| 4950 | 18.182 | 18.182 | -5.064 | 7.778 | 0 | 1.01 |
因此, 在迭代次数较少时观察到超快退火算法的显著优势。 当它增加时, 优势减少, 有时甚至转为负面。 请注意, 通过优化一个参数来测试算法时发生了类似的情况。
现在, 重点: 比较超快退火算法和遗传算法 (GA), 集成到策略测试器中。
GA 和超快退火在优化两个变量时的比较: "移动平均周期" 和 "移动平均偏移"
算法将从以下初始参数开始:
- 最大风控百分比 — 0.02; 衰减因子 — 3; 移动均线周期: 1 — 120, 步长: 1; 移动均线偏移 — 6-60, 步长: 1
- 区间: 01.01.2017 — 31.12.2017, 交易模式: 无延迟, 逐笔报价: 1 分钟 OHLC, 初始本金: 10000, 杠杆: 1:100, 货币: EURUSD
- 优化将使用最大余额标准来执行
运行遗传算法 20 次, 保存结果以及完成算法所需的平均迭代次数。
运行 20 次 GA 后, 获得以下数值: 1392.29; 1481.32; 2284.46; 1665.44; 1435.16; 1786.78; 1431.64; 1782.34; 1520.58; 1229.36; 1482.23; 1441.36; 1763.11; 2286.46; 1476.54; 1263.21; 1491.09; 1076.9; 913.42; 1391.72。
平均迭代次数: 175; 目标函数的平均值: 1529.771。
考虑到目标函数的最佳值为 2446.33, 遗传算法得出的结果并不理想, 目标函数的平均值仅为最佳值的 62.53%。
现在执行 20 次超快退火算法, 在 175 次迭代中所用参数: p1=1, p2=1。
超快退火在 4 个测试代理上启动, 而目标函数的搜索是在每个代理上自主执行的, 致使每个代理执行 43-44 次迭代。 获得了以下结果: 1996.83; 1421.87; 1391.72; 1727.38; 1330.07; 2486.46; 1687.51; 1840.69; 1687.51; 1472.19; 1665.44; 1607.19; 1496.9; 1388.37; 1496.9; 1491.09; 1552.02; 1467.08; 2446.33; 1421.15。
目标函数的平均值: 1653.735, 最佳目标函数的 67.6%, 略高于 GA 获得的目标函数。
在单个测试代理上运行超快退火算法, 执行 175 次迭代。 结果为, 目标函数的平均值为 1731.244 (最佳值的 70.8%)。
GA 和超快退火在优化四个变量时的比较: "移动平均周期", "移动平均偏移", "衰减因子" 和 "最大风控百分比"。
算法将从以下初始参数开始:
- 移动均线周期: 1 — 120, 步长: 1; 移动均线偏移 — 6-60, 步长: 1; 衰减因子: 0.02 — 0.2, 步长: 0,002; 最大风控百分比: 3-30, 步长: 0.3。
- 区间: 01.01.2017 — 31.12.2017, 交易模式: 无延迟, 逐笔报价: 1 分钟 OHLC, 初始本金: 10000, 杠杆: 1:100, 货币: EURUSD
- 优化将使用最大余额标准来执行
GA 在 4870 次迭代中完成, 最好结果为 32782.91。 由于大量可能的组合, 完整搜索无法启动; 因此, 我们将简单比较 GA 和超快退火算法的结果。
超快退火算法在 4 个测试代理上开始, 参数为 p1=0.75 和 p2=1, 且结果为 26676.22。 该算法在这些设置下表现不佳。 我们尝试通过设置 p1=2, p2=1 来加速降温。 还要注意温度计算公式:
T0*exp(-p1*exp(-p2/4)*n^0.25), 其中 n 是迭代次数,
在第一次迭代时急剧下降 (在 n=1, T=T0*0.558)。 所以, 通过设置 CoeffOfTemp=4 来增加初始温度的系数。 使用这些设置运行算法可显著改善结果: 39145.25。 下面的视频演示了该算法的操作:
参数为 p1=2, p2=1 的超快退火演示
因此, 超快退火算法是 GA 的有力竞争者, 并且能够通过正确的设置与其竞争。
结束语
本文研究了模拟退火算法及其实现, 以及与移动平均 EA 的集成。 对于移动平均 EA, 优化不同数量的参数方面, 其性能已得到测试。 此外, 还将模拟退火的性能与遗传算法的性能进行了比较。
已测试了模拟退火的各种实现: 玻尔兹曼退火, 柯西退火和超快退火。 超快退火表现出最佳结果。
以下是模拟退火的主要优点:
- 优化不同数量的参数;
- 算法参数可以被定制, 这令其可在各种优化任务中有效运用;
- 可选择算法迭代次数;
- 拥有图形界面来监视算法的操作, 显示最佳结果并回放算法运算结果。
尽管有显著的优点, 但模拟退火算法也具有以下实现缺陷:
- 该算法不能在云端进行测试;
- 与智能系统集成很复杂, 因此有必要选择参数以期获得最佳结果。
这些缺点可以通过开发通用模块来消除, 通用模块将包括用于优化智能系统参数的各种算法。 由于在测试运行后会接收到目标函数值, 因此该模块将为下次运行生成优化参数的新值。
以下文件附加到文章:
| 文件名 | 注释 |
|---|---|
| AnnealingMethod.mqh | 模拟退火算法操作所需的类应放置在 /MQL5/Include |
| FrameAnnealingMethod.mqh | 在终端窗口中显示算法执行过程的类应放置在 /MQL5/Include |
| SimpleTable.mqh | 用于处理图形界面表格的辅助类应放置在 /MQL5/Include |
| Moving Average_optim.mq5 | 移动平均 EA 的修改版本 |
| test.zip | 存档包含 TestAnnealing.mq5 EA 以及辅助文件, 可从测试文件加载输入数据, 并测试模拟退火算法 |
| AnnealingMethod.zip | Zip 文件内含创建播放器界面的图像。 该文件应该放在 MQL5/Images/AnnealingMethod |


